2013年高考数学三角函数问题赏析及启示

2013-09-17安徽省六安市第二中学杨兴军邮编237005

中学数学教学 2013年6期

关键词：图象解析试题

安徽省六安市第二中学吴斌杨兴军（邮编：237005）

三角函数是中学数学的主体内容，是高考的重点.近几年高考已摒弃了对复杂三角变换和特殊技巧的考查，将重心转移到三角函数的图象与性质的考查，对基础知识和基本技能、基本思想的考查上，分析2013年高考题中的三角函数试题，可归纳为以下几种类型.

1 纯三角问题

1.1 考查三角函数的图象与性质

例1 （2013年高考大纲卷理12）已知函数f（x）＝cosxsin2x，下列结论中错误的是（）

A.y＝f（x）的图象关于点（π，0）中心对称

B.y＝f（x）的图象关于直线x＝对称

C.f（x）的最大值为

D.f（x）既是奇函数，又是周期函数

解析1 （排除法）

因为f（π＋x）＋f（π－x）＝0，所以f（x）关于点（π，0）中心对称，排除选项A；

因为f（＋x）＝f（－x）＝sinxsin2x，所以f（x）关于直线x＝对称，排除选项B；

由正、余弦函数性质可知，f（x）既是奇函数，又是周期函数，排除选项D.

解析2 （直接法）

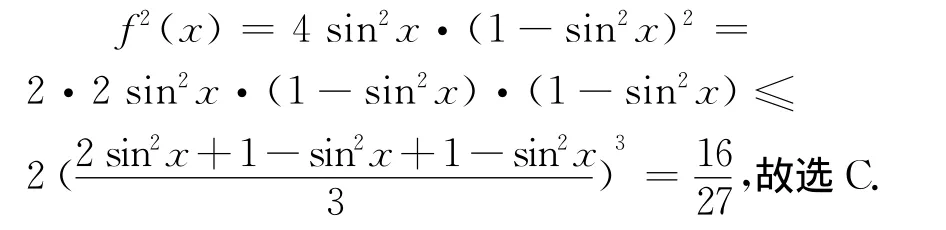
评注此函数不是标准型三角函数y＝Asin（ωx＋φ）（或y＝Acos（ωx＋φ）），一般不能用它们的相应结论，可用下式检验其性质：

f（a＋x）＋f（a－x）＝0⇔f（x）关于点（a，0）对称；

f（a＋x）－f（a－x）＝0⇔f（x）关于直线x＝a对称；

至于周期性、奇偶性可用定义判断.

1.2 考查三角函数的图象与解析式

例2 （2013年高考四川卷，理5）函数f（x）＝2sin（ωx＋φ）（ω＞0，－＜φ＜）的部分图象如图所示，则ω，φ的值分别是（）

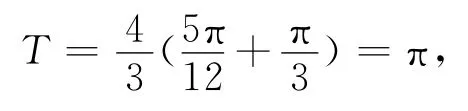
评注利用图象求y＝Asin（ωx＋φ）（A＞0，ω＞0）的解析式主要从以下三个方面考虑：（1）根据最大值或最小值求出A的值；（2）根据周期求出ω的值；（3）根据函数图象上某一特殊点（若是最值点或与y轴交点就用代入法，若是与x轴交点，可用五点法）求出φ的值.

1.3 考查三角恒等变换

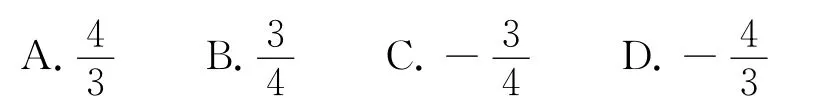
解析1 （直接法）两边平方，再同时除以cos2α，解得tanα＝3或－，由倍角公式得tan2α＝－.

例5 （2013年高考重庆卷，理9）4cos 50°－tan 40°＝（）

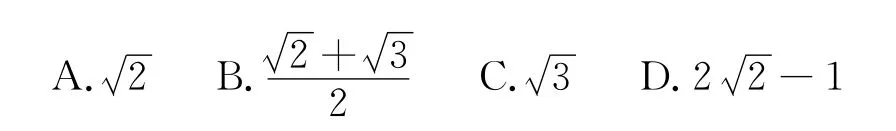
评注三角恒等变换的通性通法是：从函数的名、角、次三方面进行差异分析，再利用三角变换使异名化同名、异角化同角、高次化低次等，化角时“换元法”、“拼凑法”需强化.如考题：

2 与其他知识的综合

2.1 与数列、方程、导数的综合

例5 （2013年高考福建卷，理20）已知函数f（x）＝sin（ωx＋φ）（ω＞0，0＜φ＜π）的周期为π，图象的一个对称中心为（，0），将函数f（x）图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将所得到的图象向右平移个单位长度后得到函数g（x）的图象.

（Ⅰ）求函数f（x）与g（x）的解析式；

（Ⅲ）求实数a与正整数n，使得F（x）＝f（x）＋ag（x）在（0，nπ）内恰有2013个零点.

解析 1 （Ⅰ）f（x）＝ cos2x，g（x）＝sinx（过程略）；

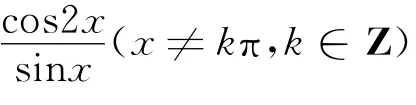
解析2 仅分析（Ⅲ），依题意，F（x）＝asinx＋cos2x＝－2sin2x＋asinx＋1.

设t＝sinx，F（x）＝p（t）＝－2t2＋at＋1（－1≤t≤1），借助图象利用x、t、F（x）之间对应关系可知a≠±1时，函数F（x）在（0，nπ）总有偶数个零点（不合题意）；而a＝±1时，情况同解析1.

说明本题考查的知识、方法、思想都很丰富，综合性强，考生答题效果较差，但知识交汇方式比较新颖，值得关注.

2.2 与函数的综合

A.［1，e］ B.［e－1－1，1］

C.［1，e＋1］ D.［e－1－1，e＋1］

解析因为y0＝sinx0∈［－1，1］，而f（x）≥0，f（f（y0））＝y0，所以y0∈ ［0，1］.

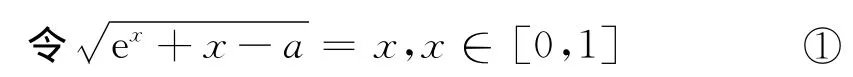
所以问题化为①有解，即ex＋x－x2＝a在x∈［0，1］上有解，令g（x）＝ex＋x－x2，由导数知识（二次求导）可知g（x）在［0，1］上单调递增，所以g（0）≤a≤g（1），故选A.

说明学生解决本题时，主要障碍是不能正确获得y0的范围以及将原问题化为①有解.

2.3 与常用逻辑用语的综合

例7 （2013年高考北京卷，理3）“φ＝π”是“曲线y＝sin（2x＋φ）过坐标原点”的（）

A.充分而不必要条件

B.必要而不充分条件

C.充分必要条件

D.既不充分又不必要条件

解析由sinφ＝0可得φ＝kπ（k∈Z），此为曲线y＝sin（2x＋φ）过坐标原点的充要条件，故选A.

2.4 与平面向量的综合

例8 （2013年高考辽宁卷，理17）设向量a＝（sinx，sinx），b＝（cosx，sinx），x∈.（Ⅰ）若，求x的值；（Ⅱ）设函数f（x）＝a·b，求f（x）的最大值.

2.5 与解三角形、不等式的综合

例9 （2013年高考全国卷 Ⅱ，理17）ΔABC的内角A、B、C的对边分别是a、b、c，已知a＝bcosC＋csinB.

（Ⅰ）求B；

（Ⅱ）若b＝2，求ΔABC面积的最大值.

解析（Ⅰ）由已知及正弦定理得

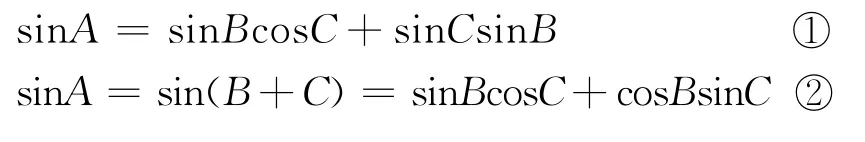
由 ①② 和C∈ （0，π）得sinB＝cosB.

又B∈ （0，π），所以B＝.

说明三角题一般用平面向量进行“包装”，讲究知识的交汇性，或将三角函数与解三角形“纵联横拓”，讲究知识的系统性，是高考题中必考内容，大部分以解答题的形式出现.

3 两点启示

3.1 “坚持以本为本”.

这不应是一句空话，2010年四川省考余弦差角公式，50万考生完全做对的不到500人，2011年陕西省考余弦定理证明，结果也很不理想，只有0.45的得分率（均分5.43分，其中的4分还是要求学生叙述定理的得分）.“坚持以本为本”就是要坚持“三基”的教学，要狠抓基本知识，基本方法，基本思想的教学；就是要坚持“过程的教学”，注意知识发生发展的过程，充分挖掘课本中每一个概念的内涵及与它相关联的知识之间的联系，形成知识网络；就是要坚持“数学本质的教学”，近几年各地高考命题作了些有益的尝试，如试题中出现了不少考查数学概念的本质，学生若能抓住数学概念的本质，把题看“化”，也就能很快看出思路、方法、结果，从而提高解题速度、效率，高考对中学教学具有反拨作用，希望老师们能关注.