浅谈培养学生独立思考问题的习惯

四川省宣汉县中小学教学研究室 赵绪昌 （邮编：636150）

数学课堂上，当老师或学生讲解完一个问题时，我们经常会听到这样两句话：“同学们，这个问题你听明白了吗？这个同学的回答你同意吗？”大部分学生都会说“明白了，我同意”.细细想想，这里的“明白与同意”包含三种情况：一是答案做对的学生以为自己懂了，不再思考解题过程中可能存在的问题或其他方法；二是似懂非懂的学生可能会受到他人的影响，自己没有真正去思考问题，而是从正确答案出发去“理解”，也不再提出疑问；三是一点也不懂的学生，觉得别人都懂了，自己也“不好意思不明白”，或者根本不知道自己哪里不懂，就更不知道如何向老师提问了.这种“从众”现象是由多种原因产生的，久而久之，会形成“尖子生跟老师走，中等生被尖子生的思维左右，后进生不知如何是好”的局面，使部分学生缺失独立思考的习惯和能力，不愿多思，不会深思，人云亦云.

宋代教育家程颐认为，“为学之道，必本于思，思则得之，不思则不得也”，“不深思而得者，其得易失”.这些都突出了思考在学习中的地位.《数学课程标准（2011年版）》中明确“数学思考”是数学学科四大方面的目标之一，“独立思考、学会思考是创新的核心”，希望学生“学会独立思考、主动探究、合作交流……”.其实，从更广泛的意义上，恰如伟大的数学家波利亚认为数学教育的根本宗旨是“教会年轻人思考”.在数学课堂教学中，如何培养学生独立思考的习惯？笔者认为，不妨从以下四个方面着手.

1 多给学生独立思考的时间

有人评价以前的课堂是“满堂灌”，现在是“满堂问”，都是压缩了学生独立思考的时间.为此，教师要善于多提富有思考价值的“大”问题，减少“打乒乓球式”的你来我往的“小”问题，引导学生围绕主要问题作深入思考.如在“直线的方程”的教学中，为了得到直线的点斜式方程，一位老师设计了如下问题：已知直线l的斜率为－1，且过点A（－2，3），若点P（x，y）（不与A点重合）在直线l上运动，则P点的坐标（x，y）满足什么条件？这个问题比较开放，学生很快从斜率公式及一次函数两个角度得出结论，在此基础上，教师追问：题中的条件“不与A点重合”是否有必要？使学生的思维得以深入.当然，如果该老师直接用“已知直线l的斜率为－1，且过点A（－2，3），若点P（x，y）在直线l上运动，则P点的坐标（x，y）满足什么条件？”会使问题更具开放性，从而更有利于学生的思维的拓展与深入.

同样，对于学生的回答，教师也不能简单地问“你明白了吗”.教师要学会延迟判断，研究表明，当教师把等待时间从3秒提高到5秒时，就会出现下面一些结果：学生回答问题的时间增加，回答不出问题的情况减少，学生提出更多的问题，主动回答问题的情况增多，学生的自信心提高等.教师也要善于补问和追问，将问题引向深处，让学生体会思考的价值.如南京师范大学附属中学陶维林老师在教学“函数概念”一课时，先让学生举几个函数的例子（因初中已学过“函数”），学生每举出一个例子，他就追问举例的学生：“你凭什么说自己举的例子表示一个函数？其他学生也思考一下，他所举的是函数的例子吗？为什么？”然后根据学生所举例子，引导他们明确分别用解析式、图象、表格表示对应关系的函数.由于学生所举例子都是用解析式表示的，于是他接着问：“函数关系都是可以用解析式表示的吗？”引导学生开阔思路，再举一些用图象、表格表示对应关系的函数.陶老师自己也参与举例，并让学生来判断他举出的例子是否能够表示一个函数，说明理由.这样的设问与追问，学生思维参与度高，始终保持一种持久、亢奋的学习状态.无疑，教学取得了很好的效果.

2 打开学生独立思考的空间

在教学中，笔者发现，当一题有三解、四解甚至五解时，学生往往会更有思考的冲动，学习的情绪也更高涨.究其原因，是开放题打开了学生独立思考的空间.依此类推，要求学生独立思考，教师在教学方式上首先要努力走向开放.课堂决不能是“一言堂”，否则学生的独立性就是无源之水.教师的讲解也不宜过细，要给学生留有思考、探究和自我开拓的余地.否则，看似讲透，实则难以内化为学生的观点，学生的独立思考能力也无法形成.

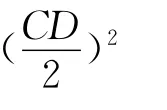
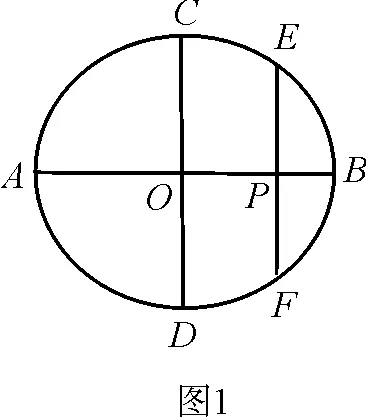
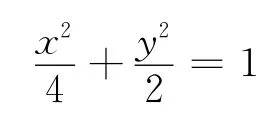
3 教给学生独立思考的基本方法

数学问题解决与数学思考是紧密相联的.在问题解决的教学中，教师不能仅仅关注问题是否解决（结果），因为解决问题过程中所形成的基本策略与活动经验才是后续学习所必需的.

比如，根据波利亚的“怎样解题表”，我们可以向学生提出以下问题：（1）本题告诉我们什么信息？要解决什么问题？信息和问题之间有什么联系？又有什么差异？（2）你知道哪些与本题有关的问题？能不能重新叙述这个问题？能不能想出一个更容易解决的问题？一个更一般的问题？一个类似的问题？（3）能否找到一个解决计划并实施这一计划？学生经常经历这样的独立思考过程，也就逐步学会了如何寻求解题策略的方法.在解题回顾时，还可以问学生：（1）能检验你的结果吗？能说出你解题过程中走过的弯路吗？能总结解题的主要经验吗？（2）能否用其他的方法得出结果？（3）能否用这一结果或方法解决别的问题呢？这样的一个问题表，正是引导学生独立思考的框架，是独立思考的外在形式.学生一旦养成这种自问自答习惯，其独立思考的能力也就大大提升.

让学生养成自我提问的习惯，学会用正确有效的提问方法来进行思考，非常重要.

（1）关于数学基本概念的自我提问方法：

如何理解这个概念？（在有关叙述中找出句子的主要成分，再找出关键的字和词）

现在我能理解这个概念了吗？（尝试复述一遍）

怎样用数学符号表述这个概念？

这个概念的内涵是什么？外延是什么？

与这个概念相似的概念还学过哪些？学过哪些与这个概念相关的概念？

找一些不符合此概念的例子并说明为什么？

（2）学习数学定理的自我提问方法：

这个定理说明的是什么？（若不清楚，再仔细阅读一遍）

这个定理是怎样提出来的？（是根据生活中的实际问题还是已学过的数学知识）

我能复述这个定理吗？

怎样用数学符号表述这个定理？

这个定理适用范围是什么？

这个定理应用的前提是什么？

能用这个定理解决相关问题了吗？（做有关的练习进行检查）

能用这个定理解决实际生活中的哪些问题？

（3）对解决问题思路的自我提问方法：

本题是怎么做的？

哪些措施起了作用？

哪些措施没起作用？

下次我该采用什么措施？

不这样做行不行？还有无别的方法？这些方法哪个最好？

该题未做对，教师讲解后分析：做不对的原因是知识欠缺？解题方法错误？思维方式不对？或是别的错误？

（4）单元复习的自我提问方法：

我是否明确本单元的学习目标？

我是否理解本单元的教学内容？

本单元都有哪些题型？

特定的问题是用什么特定的方法解决的？

本单元的学习过程中都有哪些失误，今后怎样避免这些失误？

本单元的知识哪些来源于生活实际？这些知识又能进一步解决生活中的哪些问题？

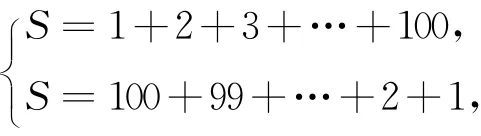
4 培养学生长时间思考一个问题的良好习惯

数学老师要尝试学会长时间地思考一个问题，想深想透，对自己的专业发展十分有利，更会改变一个人的思维方式.对于学生而言，思考时间的长短也许不是最重要的，能不能持续地关注与思考一个问题，却是能够逐步培养的.

比如，当学生面临一个数学问题时，能不能从审题开始，到提出解题策略，再到有条理地阐述解题过程与反思，这样的一个过程时间可能不长，但却是长时间思考一个问题的缩影.如在“数列”一章的复习课将要结束时，一位教师给学生留了这样的课外探究问题：仿照等差数列、等比数列的定义，给出等和数列、等积数列的“定义”，仿照研究等差数列和等比数列的方法研究等和数列和等积数列.要求以小组为单位，上交探究报告.一星期后，每个小组都上交了他们的探究成果.仿照等差数列和等比数列的定义，学生定义等和（积）数列为：如果一个数列从第二项起，每一项与它前一项的和（积）是一个常数，那么这个数列是等和（积）数列，并规定这个和（积）是等和（积）数列的公和（公积），记作D（Q）.综合学生的探究报告，他们研究了下列问题：①公和为0时，数列的项的特点和前n项和；②公和不为0，首项为0时，数列的项的特点和前n项和；③什么情况下等和数列是常数列；④等和数列的一般通项公式；⑤公积为0，首项不为0时，等积数列项的特点和前n项和的情况；⑥首项为0时，等积数列项的特点和前n项和的情况；⑦公积不为0，首项不为0时，等积数列项的特点和前n项和的情况；⑧什么情况下等积数列是常数列；⑨等积数列的一般通项公式.有一个小组（学习成绩较好）甚至意犹未尽的又提出了一个二阶等差数列的模型.学生的表现出乎笔者的意料.虽然囿于知识积累的限制，学生对较为复杂问题的探究结果不如简单问题漂亮，但笔者认为：独立思考是一种注重过程、以学生参与获得数学体验为主要目标的学习方式，而不应以探究结果“好坏”论成败.对于学生来说，任何独自发现或创造出来的成果都是值得肯定的.

作为教师，要有意识地引导学生完整地思考一个问题，鼓励学生用自己的方法，主动将新学的知识和以往的知识沟通.在这个过程当中，学生的思维会跳出对一题一解的关注，获得专注思考的经历和良好的思考习惯.

1 张洪魏.关于学生数学认知理解的思考［J］.数学教育学报（津），2006（4）

2 凌明灿.论数学教师如何成为有效的课堂“引导者”［J］.中学数学（高中版），2011（1）

3 王文森.学生真的明白了吗？——培养学生独立的数学思考习惯之我见［J］.小学数学教师，2012（9）