基于空间位置关系的纤维形态研究
2013-09-16陈梦睿曾培峰
陈梦睿,彭 轶,曾培峰
(东华大学a.计算机科学与技术学院;b.信息科学与技术学院,上海 201620)
纤维长度反映纤维及其成纱的质量,直接影响纤维的可纺性和加工的有效性,其是纺织原料、精纺加工质量检验的必测项目.纤维长度在工艺上起着重要作用,针对不同类型的纤维可以通过调节纺织机械提高加工效率,因此,精确计算纤维长度是纺织品质量检测的重要研究课题.纤维长度计算需要纤维样本,现有纤维样本制作工艺获得的纤维样本存在一定的交叉现象.精确计算纤维长度的前提是能够精确地分离交叉纤维[1],而交叉纤维分离的难点是在图像中识别交叉纤维与分叉纤维.
纤维分离是图像分割技术的一种特殊应用.目前,国内外关于图像分割技术的研究已经非常多[2],但是对于纤维这类细长目标的分割研究尚未形成一定的规模.纤维分离的关键是交叉纤维和分叉纤维的特征提取系统.目前应用较为广泛的是基于交叉处各分支斜率的分离算法[3-5],这种依靠重叠处纤维分支的斜率方法,用相近的斜率进行匹配,对3根以内交叉纤维的正确率较高,但无法区分分叉纤维和交叉纤维.文献[6]通过提取纤维集合体边缘,计算边缘各点倾角曲线,对曲线进行小波变换去除纤维头端,获得纤维纵向边缘,用Hough变换提取直线逼近纵向边缘,对提取的纵向边缘进行分解合并和配对,但这种方法对纵向边缘固有天然转曲的棉纤维、细羊毛等纤维的分离效果较差.文献[7]以纸浆纤维为例,针对图像的方向特性,使用基于Curvelet变换的图像预处理方法,结合纤维的宽度信息识别分叉纤维和交叉纤维,但这种方法的时效性与通用性有待改进.
本文在二维空间纤维分离算法的基础上,引入纤维图像的三维空间参数,对不同焦距下采集的大景深(depth of field)[8]纤维图像序列,根据交叉纤维和分叉纤维不同分支的聚焦清晰度情况,从中提取交叉纤维的逻辑匹配关系,获取纤维景深方向上的有效信息,为纤维分离提供特征参数.由于交叉纤维在空间z方向上存在明显的上下关系,而分叉纤维在空间z方向上处于同平面,因此,本文提出的纤维三维特征参数提取方法能正确区分交叉纤维和分叉纤维,为后续纤维分离算法提供正确、有效的信息.
1 算法原理
交叉纤维和分叉纤维的区别:交叉纤维分属于不同的平面,两根或两根以上的纤维存在重叠现象,即一根纤维压在另一根纤维上面;分叉纤维在同一个平面,两根或两根以上的纤维只在某些部分相接触.这种区别通过人的视觉非常容易区分,但是在图像处理系统中很难实现自动区分.通过对同一纤维样本不同景深显微图像观察,发现在得到的纤维图像中,分叉纤维在同一幅图像中的清晰度基本一致;交叉纤维因其目标的纵向深度存在一定的差异,在同一幅图像中会出现部分清晰、部分不清晰的多焦面现象.这是由于交叉纤维对应显微镜的焦点不同,所以无法在同一个焦距下实现一致的聚焦效果.
通过分析纤维显微图像存在多焦面的成因,利用互相重叠纤维在x和y平面上具有相同的坐标,而在z方向具有不同的深度的特点,在图像特征提取过程中引入z方向参数.本文算法通过对同一观测目标拍摄不同聚焦的纤维图像,从中得到图像各像素点的z方向参数,根据纤维z方向的信息对纤维交叉部分进行分层,构建三维模型,为后续纤维分离提供特征参数,从而实现单根纤维的分离.
2 特征参数提取算法
2.1 清晰度定义
数字图像常用的清晰度函数包括梯度函数、频谱函数和熵函数[9].其中,梯度函数运算速度最快,从检测的实时性考虑,本文采用梯度函数获取图像像素点的清晰度.像素点的z方向参数定义为图像成像最清晰点所位于的图层号,因而首先需要确定用于表征像素级图像清晰程度的参数.以人眼视觉特性,通过观察图像的目标与背景的边缘观测目标的清晰程度,边缘锐利,图像比较清晰;边缘过度平缓,图像比较模糊.图像的清晰度表明目标与背景在灰度上的差异.鉴于清晰度的旋转不变性,定义归一化的清晰度计算式如下:
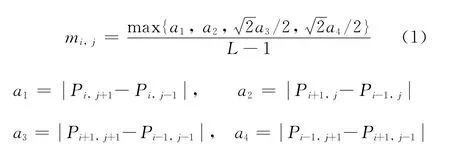
式中:Pi,j为像素点 (i,j)的灰度值;a1,a2,a3,a4分别表示目标像素点垂直、水平、两个斜向的灰度变化率;L为图像的灰度级数.mi,j为像素点 (i,j)的清晰度,范围为 [0,1],mi,j=1表明该点清晰度最高,mi,j=0对应最模糊状态.
2.2 清晰度计算
根据上述清晰度的定义,可以分别对纤维图像进行横向和纵向清晰度计算.横向计算即对每幅纤维图像的各个像素点计算清晰度,区分纤维的边缘、目标内部和背景;纵向计算即对一组同处于一个前景的不同聚焦纤维图像上,找出每一像素点清晰度极大值所对应的图层位置.
本文采用30张具有相同前景、不同聚焦的纤维图像作为分析对象.首先通过式(1)计算每幅图上每个像素点的清晰度,然后在30幅图中求取同一个像素点清晰度的极大值和极大值所在的图层号.
为保存每一像素点的清晰度极大值和其所对应的图层信息,需要创建两张与图像长度相同的表:M表和I表.M表存储每个像素点聚焦状态下的清晰度值;I表存储每个像素点聚焦的图层号.根据像素点清晰度值的变化,确定像素点聚焦情况,当其清晰度值达到最大之时,像素点为聚焦状态.
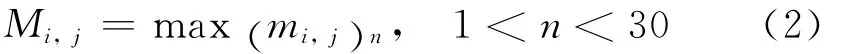
M表中保存30幅图像中同一位置像素点的清晰度极大值Mi,j,即式中:Mi,j为像素点 (i,j)的清晰度极大值;n为图层号;(mi,j)n表示像素点 (i,j)在第n幅图的清晰度值.
I表中保存30幅图像中同一位置像素点清晰度极大值Mi,j所在的图层号Ii,j,即
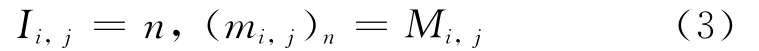
通过式(2)和(3)计算,获得 M表和I表的数据,两张表格数据输出的图像如图1所示.
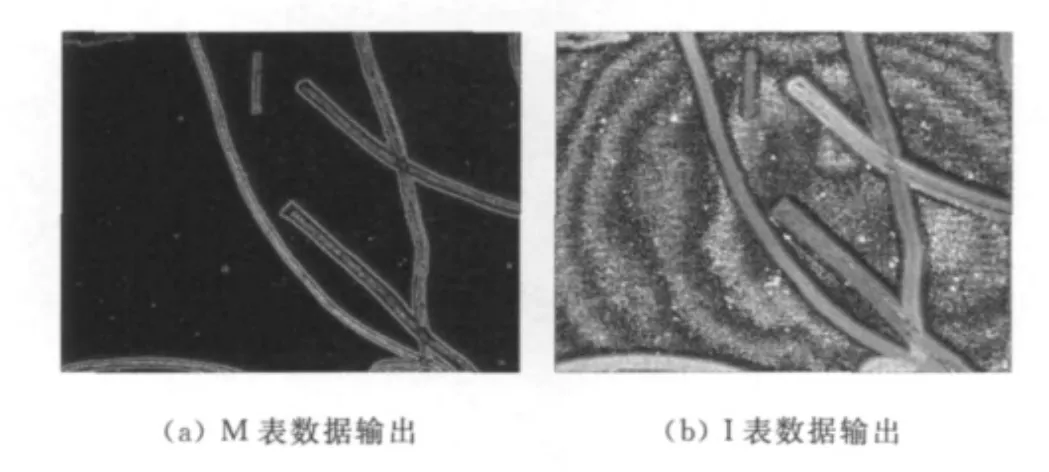
图1 清晰度计算结果Fig.1 Result of definition calculation
由图1(a)可知,由于纤维样本中背景部分的像素点灰度值差异较小,导致背景部分的清晰度值较小,在图中基本呈现黑色;纤维部分、尤其是纤维边缘部分的像素点灰度值差异较大,导致纤维部分的清晰度值较大,在图中呈现浅色.由图1(b)可知,同一根纤维的清晰度极大值所处的图层号基本一致,不同纤维清晰度极大值的图层号差异较明显,背景部分相邻像素点差异也较大,这些差异正是样本图像在z方向值的体现.
2.3 清晰度计算算法优化
M表中每个像素点的清晰度是30幅图中对应位置的清晰度极大值,I表是30幅图中每个像素点的清晰度极大值所在的图层号,必须对每幅图像的每个像素点计算清晰度,清晰度极大值和对应的图层号必须等待30幅图像全部传输完毕后才能进行比较.这种处理方法因数据处理量多、计算量大、处理速度慢,无法实现实时数据处理.
在纤维样本显微图像拍摄的过程中,显微镜纵向移动是单向移动的,图像上每个像素点的清晰度的变化趋势一般为不清晰-清晰-不清晰,这为提高算法的效率提供了改进思路.
图2所示为纤维某一像素点的清晰度的变化曲
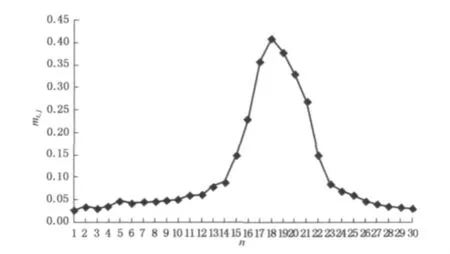
图2 纤维某一像素点清晰度-图层关系曲线Fig.2 The relationship of definition and layer index of a fiber pixel
线.由图2可知,该像素点在30幅图像中经历了模糊到清晰再到模糊的过程,在第17幅图上其清晰度值达到最大,表明在这个图层上该点最清晰.因此可以对算法进行改进,在采集每幅显微图像的同时,计算并比较每个像素点在不同图层中的清晰度值,一旦找到了某一点的清晰度极大值,则将这个清晰度值和对应的图层号记录到M表和I表的对应位置中,并停止计算后续的图层中该位置像素点的清晰度值.从理论上分析,当某点的清晰度值到达最大以后出现下降趋势时,该最大值点即为最清晰点.但是在图像拍摄过程中不可避免会有光学系统产生的噪声随机叠加在图像上,导致错误输出.为确保得到正确的结果,对像素点达到最清晰状态的判断条件附加约束条件,即只有当该像素点的清晰度达到极大值并在后续的2幅图像中连续下降,方能将这个极大值定义为清晰状态的清晰度值.
改进算法得到的M表和I表的数据输出结果如图3所示,和原算法得到的结果(图1所示)基本一致.
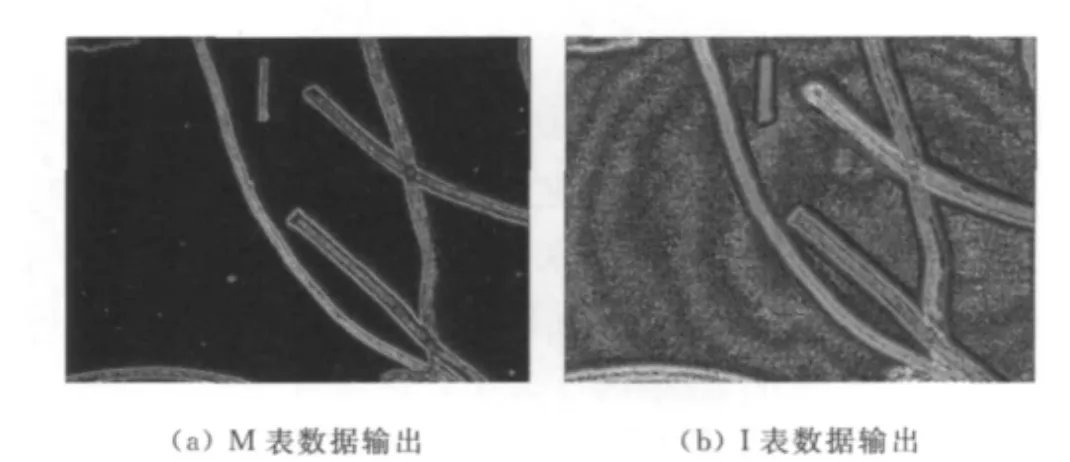
图3 算法改进后的清晰度计算结果Fig.3 Result of definition calculation with optimization
对改进后的算法进行处理信息统计,平均每个像素点进行运算比较的图层数为18.相对于改进前的每个像素点需要计算比较30幅图像而言,运算量减少为60%,处理的数据量减少很多,提高了数据处理速度.而且在第30幅图像数据处理结束的同时,M表和I表的数据也处理完毕,提高了数据处理的实时性.
2.4 背景分离
图1和图3中I表数据输出图像显示,同一根纤维的图层号基本一致,背景部分的图层号差异较大.利用这个特征,可以对纤维与背景进行分离,确定纤维的位置.
背景分离的方法是将I表中背景点的图层号置为0,保留纤维像素点的图层号.通过比较每个像素点与其邻域点图层号的差异确定背景还是纤维.合理选择模板,确定邻域点的范围,需要兼顾处理效果和处理时间.常用的邻域模板有3×3模板和5×5模板.3×3模板的处理速度快,但是效果较差;5×5模板的处理效果较为理想,处理速度也比较快.综合考虑效果和速度,选择5×5模板进行邻域处理.以点(i,j)为中心,用5×5模板计算该像素点邻域图层号的平均值如式(4)所示.
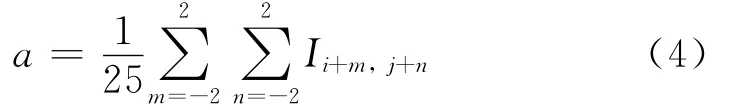
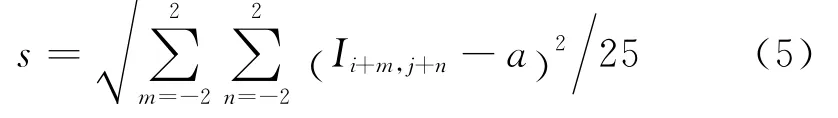
该邻域图层号的标准差计算如式(5)所示.对图1(b)用式(5)计算后得到的标准差结果输出如图4所示,图像表明纤维部分与背景部分的标准差差异较大.

图4 对图1(b)标准差计算结果输出Fig.4 Result of standard deviation of Fig.1(b)
通过Otsu算法选取阈值T1对图4进行纤维和背景的分离操作.若像素点的图层号标准差大于阈值T1,表明该点与其邻域点的相关性较差,将其标记为背景点,相应的图层号记为0,否则保留原来的图层号.即满足:
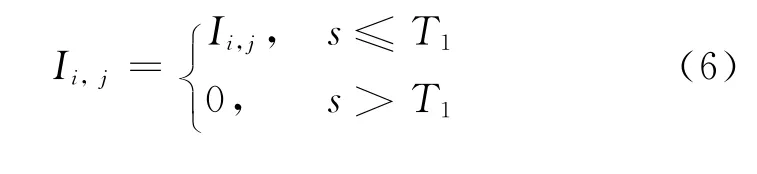
对图1(b)所示的I表数据进行背景分离处理的结果如图5所示.由图5可以看出,虽然纤维的形态得到较好的保留,但是同一纤维相邻像素点的图层号存在一定的差异,效果并不理想.
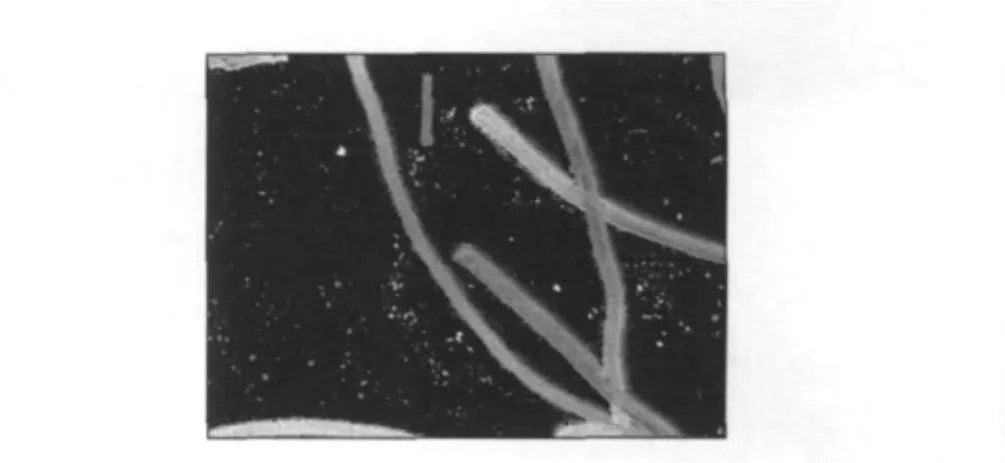
图5 对图1(b)进行背景分离处理结果Fig.5 Result of Fig.1(b)background segmentation
2.5 纤维清晰度增强
没有对清晰度极大值的M表数据进行信号的去噪处理,直接通过M表数据对应的I表数据进行背景分离,导致背景分离效果不理想.在纤维显微图像拍摄过程中,显微镜点光源引起采集图像的光照不均对图像干扰,产生的噪声会影响纤维的清晰度值和图层号的计算.因此,在进行背景分离处理之前,需要对M表的数据进行纤维清晰度增强处理,滤除噪声影响,突出纤维信息.
纤维清晰度增强采用四邻域极大值增强方法.当计算点的清晰度值大于以它为中心的四邻域像素点的最大清晰度值时,保留该点的清晰度值;否则视该点为受噪声影响点,删除其清晰度数值.具体算法:逐点逐行扫描M表数据,将每个像素点清晰度值与它四邻域像素点的清晰度值进行比较,若该值为极大值,则保留该极大值,在I表中保留该点的图层信息;否则将该点的清晰度值置0,同时删除I表对应位置的图层信息.判断条件如式(7)和(8)所示.
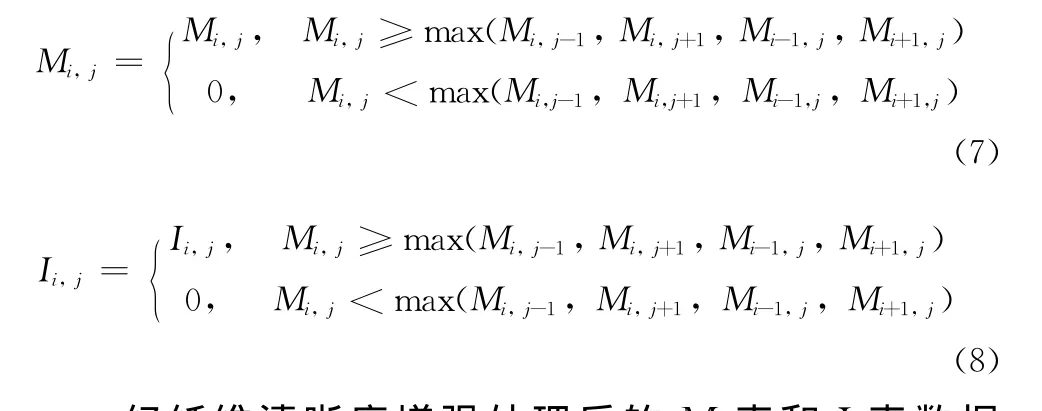
经纤维清晰度增强处理后的M表和I表数据输出结果如图6所示.对比图1的输出结果,图像中大部分噪声点被去除,提高了纤维部分图层号的一致性.

图6 纤维清晰度增强处理结果Fig.6 Result of fiber definition enhancement
2.6 纤维图像分层表示
经纤维清晰度增强处理以后,纤维的边缘部分像素点清晰度较大值被保留下来,纤维内部因有纹理其清晰度较大值也被保留下来,背景部分像素点清晰度较小值已被删除.此时可以用种子生长法进行区域填充,实现纤维图像分层表示.种子生长法常用的步长有四邻域、八邻域及四、八邻域间隔步长.这3种步长分别将图像分割为三角形形状、正方形形状、八角形形状,均能实现纤维分层.其中四邻域步长运算速度最快,从填充的结果看并不影响纤维的分层效果,因此,本文采用四邻域步长进行种子点生长处理,以提高检测系统的响应速度.具体充填步骤如下所述.
Step 1将图6(a)所示灰度值不为0的像素点标记为种子点,为0的点标记为非种子点.将种子点存入堆栈S中.
Step 2判断堆栈S是否为空.若不为空,取出堆栈顶部第一个像素点记为a,并将其从堆栈中移除,转Step 3;若堆栈为空,结束.
Step 3遍历点a的四邻域像素点,若某一邻域点为非种子点,将a的值(图层号)赋给该非种子点,同时将该非种子点标记为种子点,放入堆栈S中.转Step 2.
使用上述的种子生长法进行填充运算,结果如图7所示.

图7 填充后的I表数据输出Fig.7 Output of table I after flood-fill
图7所示的图层号清晰地显示同一根纤维相近部分图层号基本一致,而不同根的纤维尤其是交叉纤维,图层号差异明显.如图7边框标记部分所示,纤维2与纤维4图层号相似,纤维1与纤维3图层号相似,而纤维1、3与纤维2、4图层号差异较大.因而可以确定1、3为一根纤维,2、4为另一根纤维,且这两根纤维为交叉关系而非分叉关系.如果两根纤维是分叉关系,这4段纤维图层号是相似的.因此纤维图像的分层关系可以由填充后的I表数据明确表示出来.
3 结 语
本文提出的纤维三维特征参数提取算法,利用同一前景不同聚焦的一组图像,根据纤维像素点的清晰度获得纤维z方向的数值,能清晰地标注出不同纤维之间的图层号相关性,有效地区分交叉纤维和分叉纤维.根据像素点图层的清晰度,可以获得的清晰纤维图像和纤维三维特征参数,在实现大图拼接、纤维分离方面有很好的应用前景.
参 考 文 献
[1]张新峰,沈兰荪.图像分割技术研究[J].电路与系统学报,2004,16(2):19-24.
[2]ZHANG Y J.A review of recent evaluation methods for image segmentation[C]//Sixth International Symposium on Signal Processing and Its Applications.2001:148-151.
[3]RIZVANDI N,PIZURICA A,PHILIPS W.Automatic individual detection and separation of multiple overlapped nematode worms using skeleton analysis[C]//Proceedings of the 5th International Conference on Image Analysis and Recognition.Berlin:Springer-Verlag,2008:817-826.
[4]SRISANG W,JAROENSUASINEE K,JAROENSUTASINEE M.Segmentation of overlapping chromosome image using computational geometry[J].Walailak Journal of Sci & Tech,2006,3(2):181-194.
[5]VESE L A,CHAN T F.A multiphase level set framework for image segmentation using the mumford and shah model[J].International Journal of Computer Vision,2002,50(3):271-293.
[6]贾立峰.重叠纤维的分离计数算法[J].纺织学报,2011,32(5):43-49.
[7]边建美.纸浆纤维的图像分割与识别方法研究[D].济南:山东轻工业学院电子信息与控制工程学院,2009:54.
[8]许增朴,王永强,于德敏,等.三维人体表面轮廓测量系统中的“景深”问题研究[J].天津工业大学学报,2006,25(5):14-17.
[9]李奇,冯华君,徐之海,等.数字图像清晰度评价函数研究[J].光子学报,2002,31(6):736-738.
