性信息素诱捕下害虫Logistic增长及经济阈值数学模型

2013-09-15赵志国荣二花赵志红孔维娜张金桐马瑞燕

生态学报 2013年16期

赵志国，荣二花，赵志红，孔维娜，张金桐，马瑞燕，*

(1.山西农业大学农学院，太谷 030801;2.北京科技大学数理学院，北京 100083;3.山西农业科学院植物保护研究所，太原 030031)

对害虫的发生发展动态进行预测可通过构建数学模型来实现，模型的优劣能影响害虫测报的精确性［1］。害虫防治中已使用多种模型，如种群动态常用算法有人工神经网络［2］、遗传算法、模拟退火［3］、Levenberg-Marquardt算法［4］，以及Logistic模型。刘树生等研究桃蚜(Myzus persicae)在恒温下和变温下的规律发现接近经典的logistic曲线［5］，沈佐锐描述菜蚜的种群动态修正了Logistic模型［6］，尤民生等在褐飞虱种群动态模拟中使用Logistic模型［7］，程述汉等构建了作物害虫化学防治的Logistic数学模型，并应用此模型进行了相关的数据拟合，可反应用药后田间虫量的变化［8］。

通过性信息素诱捕器诱捕量对害虫的发生量进行测报是害虫综合防治的一种重要措施［9-11］。利用性信息素监测害虫中可以获知害虫的发生动态和诱捕数量，但无法获知田间实际虫量，特别是因此造成的危害无法确定，导致经济阈值也很难确定。本文将模拟性信息素诱捕害虫时田间虫量与诱捕量变化的过程，解析害虫发生时的性信息素诱捕强度、种群自然增长率、害虫发生量等生物学参数并建立数学关系。在相同的诱捕强度且虫量稳定的条件下，比较性信息素诱捕与通常诱捕方式(黑光灯［12］、糖醋酒诱捕［13］)的不同。研究控制性信息素的诱捕强度使持续诱捕量达到最大的条件，探讨最佳防治害虫效果时诱捕强度、种群增长率，并确定梨小食心虫的经济阈值，以期为性信息素防治害虫技术提供理论依据。

1 性信息素诱捕量模型

1.1 性信息素诱捕下Logistic种群模型

设t时刻田间的成虫虫量为x(t)，其中雌雄各占一半(不同昆虫要经过田间调查其性比而定)，关于x(t)的自然增长和性信息素诱捕量作如下假设:

1)在无诱捕时，昆虫种群自然发生遵循Logistic模型，x(t)的增长服从Logistic微分方程［6］。

式中，r＞0是种群固有增长率(%)，N是田间容许的最大虫量，x为田间实际虫量(头)，x'(t)为增长虫量(头)。

2)当田间虫量不是高密度时，昆虫性信息素诱捕量h(x)与田间雄虫量x(2

t)成正比［14］。

于是单位时间的诱捕量(雄虫)为:

式中，各变量的含义为:比例常数k表示单位时间诱捕率(%)。k=qE，其中E(0＜E＜1)表诱捕强度(%)，是可以控制的参数，譬如用诱捕器田间密度的诱捕效率来度量;q称性信息诱芯的诱杀系数(%)，表示单个诱芯的诱杀率。令q=1，即单个性信息素诱芯可以100%诱杀每只成虫。

由此可得当诱捕量h(x)的雄虫时，因雌雄比为1∶1则相应数量的雌虫便不能繁殖后代，那么能繁殖后代的虫量为x(t)-Ex(t)，令

式中，f(x)表示利用性信息素诱捕单位时间内增加的虫量，此时在有性信息素诱捕的情况下，田间成虫虫量满足方程:

式中，F(x)是田间诱捕后的单位时间内增加的成虫虫量(头)，从方程(4)可以从诱捕量得知的虫情动态x'(t)的变化。那么，在通常诱捕情况下(非性信息素诱捕，如黑光灯、糖醋液、食物诱饵等)，h(x)与田间成虫虫量x(t)成正比。设诱捕强度为˜E，则单位时间的诱捕量为:

由此可得到在通常诱捕情况下，田间成虫虫量满足方程:

式中，G(x)是通常诱捕后的单位时间内增加的成虫虫量(头)，从方程中可以从诱捕量得知的虫情动态x'(t)的变化。如果要知道田间的稳定的成虫虫量和保持稳定的条件，即时间t足够长后田间成虫虫量的x(t)趋向，则可以确定最大的持续诱捕量。

1.2 种群Logistic模型的平衡点

1.2.1 性信息素诱捕下的平衡点

利用性信息素诱捕和通常诱捕2种情况下寻找田间虫量模型的平衡点，并分析其稳定性，明确性信息素诱捕的优势。

利用性信息素诱捕情况下:

得到2个平衡点:

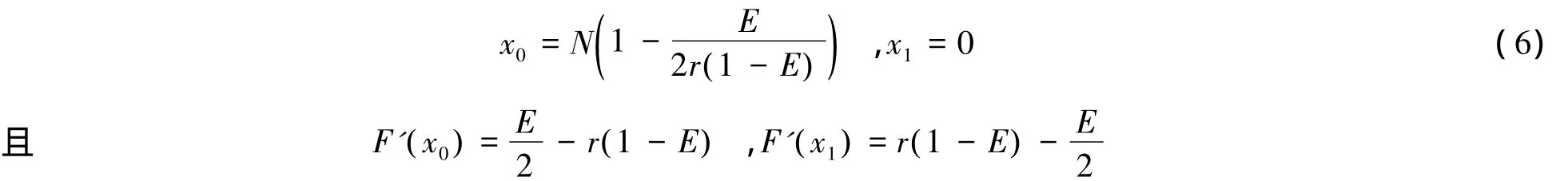
式中，F'(x0)和F'(x1)为平衡点的田间虫量的增长率(%)。

若

此时有F'( x0)＜0，F'( x1)＞0，由x(t)=x0可得出x0点稳定，x1点不稳定。

1.2.2 通常诱捕下的平衡点在通常诱捕情况下:

1.3 最大持续诱捕量的控制

进一步讨论田间成虫虫量稳定在x0前提下，如何控制诱捕强度E，使持续诱捕量最大。

且单位时间的利用性信息素诱捕和通常诱捕最大持续诱捕量分别为hmax*和hmax:

由式(2)，(5)不难算出保持田间成虫虫量在x0*的两种诱捕情况下诱捕强度E*和˜E*分别为:

式中，E*是性信息素诱捕下达到最大持续诱捕量时的诱捕强度，是通常诱捕下达到最大持续诱捕量时的诱捕强度。

因此可以看出，利用性信息素诱捕情况下，只要将诱捕强度控制在E*，或者使田间成虫虫量保持在最大虫量的一半时，可以达到持续的最大诱捕量。与通常诱捕情况相比，利用性信息素诱捕的最大诱捕量＜h，便可使田间成虫虫量保持在最大虫量一max半。另外，当虫口增长率r＜1时，有E*＜，即利用性信息素诱捕强度低于通常情况诱捕强度便可保证田间成虫虫量保持在最大虫量的一半。

图1 性信息素诱捕与通常诱捕曲线Fig．1 Curve of sex pheromone and normal trapping图中p'通常诱捕下最大持续诱捕量点，p*性信息素诱捕下最大持续诱捕量点，˜E通常诱捕下诱捕强度，E性信息素诱捕下诱捕强度，x田间实际虫量，N环境可容纳虫量，r种群固有增长率，y增加的虫量

综上所述，当田间害虫的固有增长率较小(如r＜1)时，利用性信息素诱捕成虫比通常的诱捕情况所产生的诱捕效果好，以较小的诱捕强度，便可保持持续诱捕量。

2 性信息素防治害虫的经济阈值

2.1 性信息素诱捕下的利润构成

在这个模型中，主要对利用性信息素诱捕所产生的效益进行分析。假设幼虫对田间产品进行破坏而成虫对田间产品不造成破坏。从经济角度看不追求最大的诱杀量，而考虑效益最佳。假设:

1)设昆虫雌雄比例为1∶1，幼虫存活率为SE(%)，每个雌虫的最大生殖力F(头)，最大卵量与实际卵量之比为。诱捕x雄虫所减少的幼虫为(Ex)SEFR¯［16］。

2)诱杀一头幼虫可以使田间产品得以保留并获得收入，设田间产品销售单价为P(元)，幼虫的破坏率k，记p=Pk，p是幼虫造成的损失(元)，也是杀死幼虫后获得的收入(元)。

3)开支S(元)的构成是诱捕强度的费用，如一个诱捕器的投入成本，设单位诱捕强度的费用为c(元)。

4)那么利润也就是收入T和支出S则为:

式中α=SEFR¯，则利润R为:

在稳定条件x=x0下，把(6)代入(13):

由微分法求出R'ER( )=0，R″ER( )＜0，所以ER是R E()的最大值，即ER是使得利润R E()最大的相应的诱捕强度。

将ER代入(6)式可得最大利润下的田间稳定虫量xR及单位时间的持续诱捕量hR为:

将(15)—(17)式与产量模型的(9)—(11)式相比较。可以看出当pαN＞c时，在考虑投入与产出比最小，即最大经济效益原则下，诱捕强度与持续诱捕量均有所减少，而田间虫量有所增加，显然和实际情况吻合。此时也是化学农业控制关键时期，少量化学农药即达到防治效果。

2.2 确定经济阈值

上面的效益模型是以控制害虫数量的诱捕(或称封闭式诱捕)为基础的，达不到应用性信息素诱杀害虫使田间虫量下降的目的。为达到使田间虫量下降到危害水平之下，构建大量诱捕模型，即利润与投入相同时的情况。

式(14)给出了利润与诱捕强度的关系R E()，令R E()=0的解为Es可得:

当E＜Es时，R(E)＞0，田间管理应当加强诱捕强度E，使田间虫量下降;当E＞Es时，R(E)＜0，田间管理投入过大，应当降低诱捕强度E，保证投入与产出之比。所以Es是在大量诱捕下的一个经济限阈。

图2以E为横坐标描绘了T(E)曲线图，可以看出当诱捕强度E大于时，收入出现负值。也就是说利用性信息素诱捕时，诱捕强度应小于。E也s可以由图解法得到，图3描绘了T(E)，S(E)曲线，它们的交点就是Es，其中为T(E)的最大值点，显然E*＞E^。

容易知道Es存在的必要条件是:

即售价大于(相对于总量而言)成本。并且由(18)式可知，成本越低，售价越高，则Es越大。将(18)代入(6)式得到大量诱捕下的田间稳定虫量为xs:

图2 T(E)曲线图Fig．2 T(E)curve图中E是诱捕强度，T(E)是诱捕强度下的收入，r是种群固有增长率

对于某种特定的昆虫，xs完全由成本与价格比决定，随着价格的上升和成本的下降，xs将迅速减少，出现诱捕过度，田间虫量减小，达到防治目的。

比较式(15)和(18)可知，当式(19)成立时，Es＞ER，即大量诱捕强度比最大效益下诱捕强度大。从式(18)可以得到，当，如图3中Es2，成为经济阈值;当p＞2时点Es＞E*，如图3中Es1，成为生态阈值。

3 性信息素诱捕梨小食心虫的实例

2011年4月28日—9月19日在山西省太谷县王诲庄村 (E:37°29'57.85″;N:112°37'32.80″;H:795m)的桃园中，设3种诱捕强度的不同处理，每667m2分别设5、9、13个诱捕器用于监测成虫发生。从6月27日开始调查虫果，3种不同性信息素诱捕强度下，成虫的增长量曲线与构建的Logistic曲线基本吻合，见图4。

用Origin pro 8拟合梨小食心虫Logistic增长模型，对田间调查的诱捕量进行Logistic曲线拟合，并获得梨小食心虫自然增长率r，结果为0.064(R2=0.9979)、0.065(R2=0.9982)、0.061(R2=0.9982)。应用性信息素下的经济阈值模型确定梨小食心虫的经济阈值。梨小食心虫相关生命参数已有报道［17-18］，结合测定的种群增长率，以及3种性信息素诱捕强度下的虫果率分别为16.73%、15.02%、12.44%。以2011年投入和收益市场价格为例:由于防治设施的投入及农业产品的产出单位诱捕强度的费用为c，即诱捕器的投入成本，诱捕器成本为4元/个，性诱芯为1元/个，1个世代要求换1次性诱芯，1年共换4次，费用c为40.00、72.00、104.00元。桃子价格为P，设1kg为2元，每kg有12—16个桃子，平均14个。则不同处理下的桃园中害虫造成的损失 p，结果为 186.86、323.14、237.86 元。

根据经济阈值模型，求解诱捕强度E，结果见表1。

图3 诱捕强度与经济阈值Fig．3 Trapping intensity and economic threshold图中E是诱捕强度，Es1为生态限阈，Es2为经济限阈，E^最大诱捕强度，E*最大持续诱捕量诱捕强度，r是种群固有增长率T(E)是诱捕强度下的收入，S(E)是诱捕强度下的开支，p获得的收入，a田间幼虫存在比率，N是田间容许的最大虫量，c是单位诱捕强度的费用

图4 3种诱捕强度的梨小食心虫虫量的动态Fig．4 Population of OFM under 3 trapping intensities

各处理持续诱捕量可以看出，不同诱捕强度下，其达到经济阈值时的诱捕量随诱捕器数增加而减少，13个/667m2时达到最低，5个诱捕器时最高。反映诱捕强度也经济阈值密切相关，当诱捕器量达到hd时，即为防治经济阈值，当诱捕量大于hd时则可以有效的减少田间害虫的数量，有效减少害虫虫量，达到防治的目的。

3 讨论

生态学数学模型是对种群发生和动态真实的反映，通过对害虫的种群变动规律进行研究，实现对未来害虫的发生发展动态进行预测，通过构建数学模型可以实现害虫的预测预报［19］。通过捕获害虫的数量可间接反映实际害虫发生量，是监测害虫发生的一种重要手段［20］，解决诱捕种群问题可借鉴的数学模型有经典的捕鱼模型，但和本模型相比捕获的种群明显不同，性信息素只诱捕雄虫，以较小的诱捕数量实现对种群的有效监测。性信息素监测直接反映害虫的发生动态，但传统性信息素监测害虫发生测报中，对发生期、发生量多使用经验推断。如:美国在苹果蠹蛾(Cydia pomonella)防治中，根据信息素诱捕器的诱捕数制订出经济阈值。在纽约州每20.25hm2设置一个诱捕器，其经济阈值为14头雄蛾·星期-1·诱捕器-1;而密执安州的采用每4.05 hm2设置2个苹果蠢蛾信息素诱捕器，其经济阈值为5—7头雄蛾·星期-1·诱捕器-1，这些结果都是诱捕数和危害程度资料长期积累而得出的经验值，缺乏对其它害虫实际的普遍指导意义［21-22］。基于实时、敏感、有效的性信息素监测数据，结合性信息素下害虫种群Logistic模型进行分析，及时、准确地实现对害虫危害高峰期、危害程度的测报。

表1 梨小食心虫3个诱捕强度下的E值Table 1 E value of OFM of 3 trapping intensities

表2 3种诱捕强度下达到经济阈值的持续诱捕量h RTable 2 h R value at economic threshold trapped of OFM in 3 trapping intensities

此外，性信息素诱捕以较小的诱捕强度，实现对害虫的有效的预测和控制，应用本模型不仅可确定诱捕强度的大小，精准的控制诱捕器在田间的设置数量，而且实现科学、经济的进行防控资金投入，通过大量诱捕保证害虫的防控效果，可确定防治害虫的经济阈值，达到最佳经济效益。本例中拟合梨小食心虫性信息素诱捕下的3种诱捕器强度，发现梨小食心虫诱捕量符合Logistic模型，而且同时获得性信息素诱捕下的经济阈值，使用经济阈值模型求解得到3种诱捕强度下达到经济阈值的诱捕器持续诱捕量和最佳诱捕器设置。本模型可有效的指导应用性信息素进行测报和大量诱捕防治，同时兼顾生态平衡。此模型隶属于昆虫生态学的研究，结合害虫实际发生，对性信息素进行测报有一定的理论指导意义，同时可为建立计算机预测模型和专家系统奠定基础。但在实际生产中不同昆虫有特定的特殊性，本文所拟合的梨小也仅有一年的数据为例，仍需进一步改进和修正，才能更准确有效地进行测报和大量诱捕。

致谢:感谢康乐院士对本研究的帮助，感谢山西农业大学郭玉明教授对数学模型的修正，以及李生才教授对经济阈值算法的建议。

［1］ Liu L F.Advance in research of ecological mathematical models.Chinese Journal of Ecology，1991，10(2):41-44.

［2］ Ma F，Xu X F，Zhang X L，Cheng X N.A prediction model integrating phase space reconstruction and artificial neural network and its application in pest forecasting.Acta Ecologica Sinica，2002，22(8):1297-1301.

［3］ Wang X，LüJ K，Hu X M，Xie D T.Intelligent prediction model for rice pests and its application.Transactions of the Chinese Society of Agricultural Engineering，2008，24(7):141-145.

［4］ Gao Y P，Yu H，Cui X Z，Jiang G X，Wang M N.Prediction model for rice stem borer based on L-M optimized algorithm and its preliminary application.Transactions of the Chinese Society of Agricultural Engineering，2007，23(7):162-165.

［5］ Liu SS，Meng X D.The change pattern of development rates under constant and variable temperatures in Myzus Persicae and Lipaphis Erysimi.Acta Ecologica Sinica，1989，9(2):182-190.

［6］ Shen Z R.Logistic equation revised to describe density dynamics of an Aphid population on Chinese cabbage.Journal of China Agricultural University，1985，11(3):297-304.

［7］ You M S，Pang X F.A computer simulation model of population dynamics of Brown Planthopper，Nilaparvata Lugens Stal.Entomologia Sinica，1995，2(2):163-178.

［8］ Cheng SH，Xu C S，Li M，Xin Z S，Shu H R，Wang Y A.Mathematical model of chemical control of crop pest.Transactions of the Chinese Society of Agricultural Engineering，2008，24(S2):32-35.

［9］ Byers J A.Active space of pheromone plume and its relationship to effective attraction radius in applied models.Journal of Chemical Ecology，2008，34(9):1134-1145.

［10］ Yao ST，Wu JX，Zheng Y L，Jin Z H，Lu Z J，Hu JJ，Du Y J.Application of sex pheromone of the rice leaf folder，Cnaphalocrocis medinalis(Lepidoptera:Pyralidae)in monitoring its population.Acta Entomologica Sinica，2011，54(4):490-494.

［11］ Li X，Li X W，Zhao ZG，Li J，Ma R Y，Nie L Y.Approach to improvement of using the sex pheromone lure of Carposina niponensis(Lepidotera:Carposinidae).Journal of Shanxi Agricultural University:Natural Science Edition，2011，31(3):213-216.

［12］ Lu J，Teng Z W，Tan Z J，Chen JJ.Computation and simulation of intensity distribution of black light lamp.Transactions of the Chinese Society of Agricultural Engineering，2011，27(8):247-251.

［13］ He L，Qin Y C，Zhu PX.Trapping effect of the mixture of sugar-acetic acid-ethanol to Oriental fruit moth(Grapholitha molesta)and smaller apple leaf roller(Adoxophyes orana).Chinese Bulletin of Entomology，2009，46(5):736-739.

［14］ Xue Y H，Ma R Y，Li X W，Li L，Li J.Research and application on the sex pheromone of Carposina sasakii Matsumura(Lepidoptera:Carposinidae).Chinese Journal of Biological Control，2010，26(2):211-216.

［15］ Du J，Guo JT，Zhang Y S，Wu J X.Effect of temperature on development and reproduction of Grapholitha Molesta(Busck)(Lepidoptera:Tortricidae).Acta Agriculturae Boreali-Occidentalis Sinica，2009，18(6):314-318.

［16］ Ding Y Q.Mathematical Ecology of Insects.Beijing:Science Press，1994:210-210.

［17］ Zhang X Z.A preliminary report on the study of oriental Fruit Moth(1970—1978).Journal of Plant Protection，1980，(4):254-256.

［18］ Zhang D M，Sun Y S.Linear regression equation forecast for Oriental Fruit Moth.Journal of Shandong Forestry Science and Technology，1986，(2):22-26.

［19］ Ju R H，Shen Z R.Review on insect population dynamics simulation models.Acta Ecologica Sinica，2005，25(10):2709-2716.

［20］ Johnson D T，Lewis B A，McCraw B D，Carroll B，Jervis B，Striegler K，Boozer B，Mulder P，Foshee W G，McVay J，Mizell R F III.Development and implementation of a peach Integrated Pest Management program in the Southern USA.Proceedings of the 5th International Peach Symposium，2002，592(1＆2):681-688.

［21］ Du J W.Review on the application of forecasing the insect by sex pheromone.Forecast of Disease and Pest，1990，1(1):33-38.

参考文献:

［1］刘来福.生态学数学模型的研究进展.生态学杂志，1991，10(2):41-44.

［2］马飞，许晓风，张夕林，程遐年.相空间重构与神经网络融合预测模型及其在害虫测报中的应用.生态学报，2002，22(8):1297-1301.

［3］汪璇，吕家恪，胡小梅，谢德体.水稻虫害智能预测模型及其应用.农业工程学报，2008，24(7):141-145.

［4］高艳萍，于红，崔新忠，姜国兴，王美妮.基于L-M优化算法的水稻螟虫预测模型及其初步应用.农业工程学报，2007，23(7):162-165.

［5］刘树生，孟学多.桃蚜、萝卜蚜发育速率在恒温和变温下的变化规律研究.生态学报，1989，9(2):182-190.

［6］沈佐锐.Logistic修正方程及其对菜蚜种群密度动态的描述.北京农业大学学报，1985，11(3):297-304.

［7］尤民生，庞雄飞.褐飞虱种群动态的模拟模型(英文).中国昆虫科学，1995，2(2):163-178.

［8］程述汉，徐臣善，李明，辛泽山，束怀瑞，王衍安.作物害虫化学防治的数学模型.农业工程学报，2008，24(S2):32-35.

［10］姚士桐，吴降星，郑永利，金周浩，陆志杰，胡加君，杜永均.稻纵卷叶螟性信息素在其种群监测上的应用.昆虫学报，2011，54(4):490-494.

［11］李霞，李先伟，赵志国，李捷，马瑞燕，聂磊云.桃小食心虫性诱芯合理有效使用方法的研究.山西农业大学学报:自然科学版，2011，31(3):213-216.