不同烧结温度对PMN基铁电陶瓷B位有序度的影响

2013-09-15刘敬松张敏芳游美容

无机化学学报 2013年10期

杨超刘敬松张敏芳游美容

(西南科技大学四川省非金属复合与功能材料重点实验室-省部共建国家重点实验室培育基地，绵阳621010)

铌镁酸铅Pb(Mg1/3Nb2/3)O3(PMN)是典型的弛豫铁电材料，也是非常重要的功能材料，在多层陶瓷电容器(MLCC)、高储能密度脉冲电容器、电光器件、微位移驱动器和位移器、铁电薄膜存储器等领域有着广泛的应用前景[1-4]。PMN能与钛酸铅PT(PbTiO3)固溶形成新的弛豫铁电体(1-x)PMN-x PT，它的弛豫行为直到在准同型相界附近(x=35%)才消失[5]。PMNPT因具有多变的介电和压电性能而受到广泛关注。

弛豫铁电体与正常铁电体相比，具有两个典型的特征：弥散相变和频率色散。针对弛豫铁电体的弛豫特性，国内外学者先后提出了一系列理论和模型来解释它，其中比较成熟的主要有：成分起伏理论[6]、有序-无序理论[7]、超顺电理论[8]、微畴-宏畴转变模型[9]等。其中，有序-无序理论更受青睐。

Cross[8]等较早研究了有序无序结构与介电弛豫的关系，通过改变退火条件观察Pb(Sc1/2Ta1/2)O3材料的B晶位上的有序程度与弥散相变的关系，得出结论，弥散相变与B位离子有序无序排列密切相关，无序态对应明显的弥散相变现象。一般认为，在两种离子占据 B 位的 A(B′1/3B″2/3)O3系统中，如果 B′与B″的化合价不等，则B′与B″在B位的分布应是无序的，因为要对应着电荷的平衡。但陈捷[7]等在Pb(Mg1/3Nb2/3)O3中发现了有序畴，在这些畴中，Mg2+和Nb5+以1∶1做有序排列，形成晶格周期比普通晶胞大一倍的超结构，这些超结构与基体的化学配比完全不同，因为基体材料中1∶2，而有序微区nMg∶nNb=1∶1，这就导致了电荷不平衡区的存在。而随着有序微区的增长，空间电荷产生的库仑力会阻碍有序微区的继续扩大，通过理论计算得到纯PMN的有序畴区尺寸应为6 nm左右，这与实验得出的有序畴尺寸相符合，这种纯∶1 有序结构亦被称为PMN空间电荷模型。另外，Akbas[10]等提出PMN中B位有序微区的结构是混合1∶1的，即有序微区的 B 位离子是混合有序 n(B′2/3B″1/3)1/2∶nB″1/2=1∶1，而非纯1∶1有序结构，这种有序结构在＜111＞方向上每一层的(B′2/3B″1/3)1/2亚结构中 B′和 B″是随机分布的，简言之，混合1∶1有序结构中存在随机分布的亚结构，有序中包含有无序。两种模型为解决不同的现象而存在。

研究发现，对PMN进行施主或受主掺杂可以有效弥补或加剧电荷的不平衡，从而改变材料的有序度。姚文龙[5]等分别用Li+和Yb3+对PMN-10PT进行掺杂，得出Li+能增大B位离子有序度，频率色散和弥散程度都减小；Yb3+导致B位离子有序度减小，频率色散和弥散程度都增大。Fu[11]等用La3+对PMN进行掺杂，得出La3+也能增大B位离子有序度。

CuO是很多陶瓷材料的助烧剂，如KNN-BT压电陶瓷[12]、ZnTa2O6[13]和 PMNT[14]电介质陶瓷等，都有明显地助烧效果。Wang[15]等用CuO作添加剂，使0．25PMN-0．40PT-0．35PZ 压电陶瓷的烧结温度从1 260℃降低到950℃。可是Cu离子的存在有两种形式，即Cu+和Cu2+，不同的烧结温度是否会产生不同的离子取代结果。本文使用Swartz等[16]的铌铁矿法制备PMN基铁电陶瓷，采用拉曼光谱研究不同烧结温度对 CuO 添加 0．94PMN-0．06PT(PMN-6PT)陶瓷的B位离子有序度的影响。

1 实验部分

以分析纯的 PbO、Nb2O5、MgO、TiO2、CuO 为原料，材料的基本组成可表示为：PMN-6PT-x CuO，其中 CuO 的添加量分别是 0、0．015、0．03 和 0．06 mol，采用铌铁矿法制备PMN-6PT-x CuO粉体。制备工艺如下：MgO和Nb2O5按计量比在1 100℃下反应6 h制得 MgNb5O6(MN)备用；再用 MN前驱体、PbO、PT在 850℃下煅烧 2 h制得 0．94PMN-0．06PT陶瓷粉料，合成的PMN-6PT与CuO混磨，干燥后在650℃下保温1 h。最后，加入PVA造粒，在120 MPa下压制成Ф30 mm的圆片，用双坩埚密封法，将其埋于锆酸铅粉末中，在不同烧结温度下保温4 h烧成。烧成的陶瓷片经打磨抛光，涂覆银浆，550℃烧银。

采用日本理学Rigaku D/max-RB型X射线衍射仪 (XRD)对样品的组成及结构进行分析，使用Renishaw InVia型激光Raman光谱仪 (激发波长514．5 nm，极化模式XZZY)对样品进行拉曼光谱分析，再使用Agilent 4284精密LCR仪对部分样品做介温分析(1 kHz)。

2 结果与讨论

2.1 物相分析

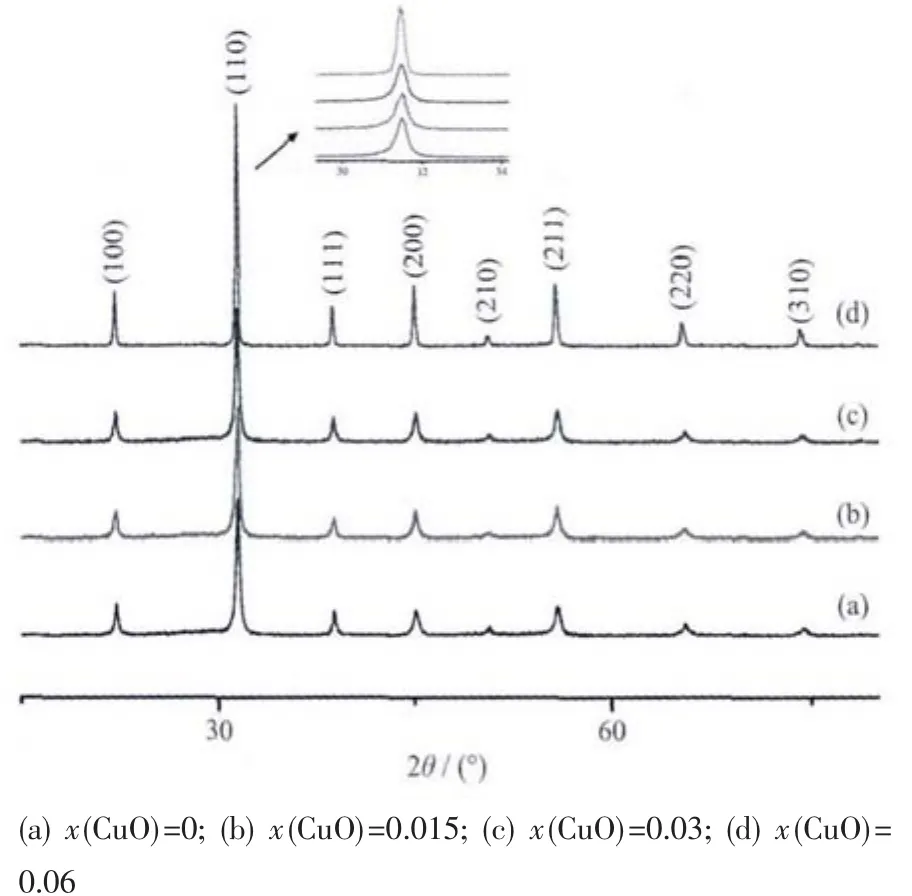
图1 烧结温度950℃下各样品的XRD图Fig．1 XRD patterns of samples sintered at 950 ℃

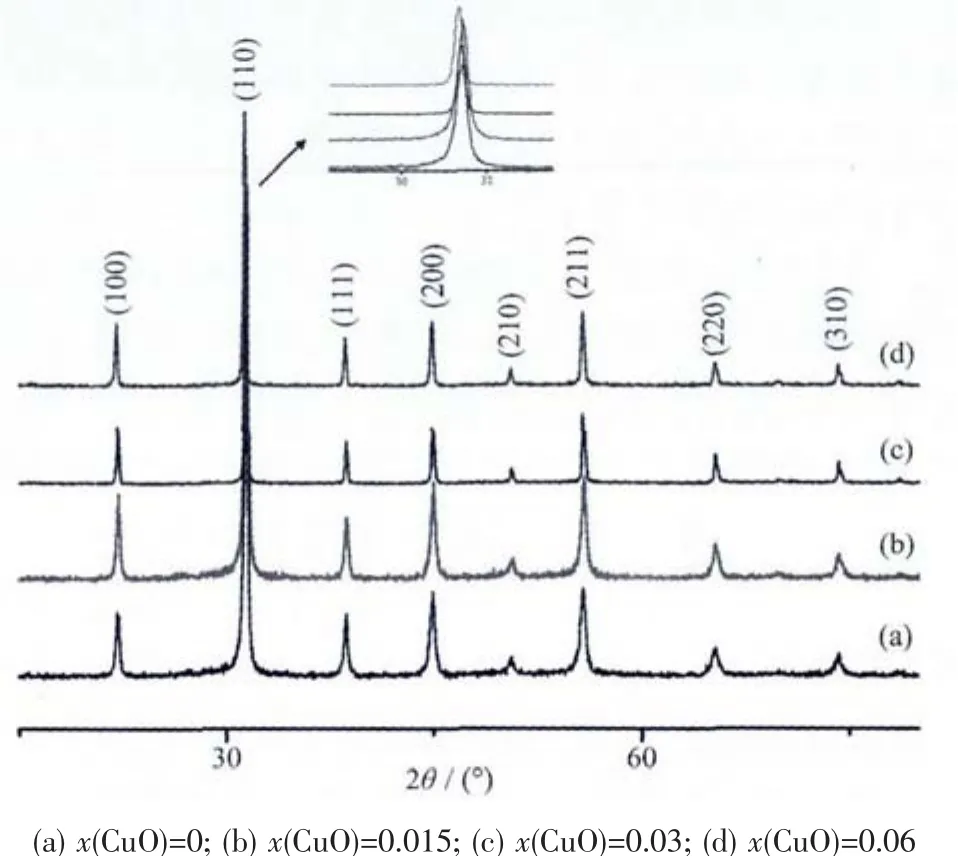
图2 烧结温度1 080℃下各样品的XRD图Fig．2 XRD patterns of samples sintered at 1 080 ℃

图1 和图2是不同烧结温度下各样品陶瓷粉末的XRD图。与标准XRD卡片对比发现：合成的样品都是单一的钙钛矿相，没有焦绿石相出现。用XRD数据计算样品的晶格参数和晶胞体积发现，掺入不同含量的CuO和采用不同的烧结温度后，晶格都发生了畸变，说明部分Cu离子进入晶格并产生了影响。根据洪特规则，全满时能量最低，Cu+(3s23p63d10)比Cu2+(3s23p63d9)更加稳定，由热力学数据计算，当温度超过1 273 K时，CuO就会分解生成Cu2O，关于CuO的高温分解已有报道[17]。根据晶体化学置换的原则，金属阳离子更容易取代电价和离子半径相近的离子，那么掺入CuO后，晶格常数变化，认为是950℃下，主要是Cu2+(半径为0．073 nm)进入晶格，而1 080℃下，主要是Cu+(半径为0．077 nm)进入晶格，它们都取代 Mg2+(半径为 0．072 nm)离子。

2.2 拉曼光谱

图3和图4为不同烧结温度所得陶瓷样品的室温拉曼光谱图。Husson[18]总结了PMN的拉曼光谱表征如下：频率260、500～600和780附近对应的分别是O-B-O弯曲振动模、Nb-O-Nb伸缩振动模和Nb-O-Mg弯曲振动模(A1g模)，也就是图中的 A、B、C峰。当极化模式为XZZY、温度范围在77～347℃时，Nb-O-Nb伸缩模对应的B峰不分裂；当温度低于77℃，B 峰分裂成 2 个峰 B1、B2(在 500～600 cm-1)[19]。表1列出了不同烧结温度下各样品的拉曼特征峰。可以看到，不同的烧结温度，3个特征峰对应的形状和频率都不一样，这也暗示了Cu离子进入晶格的形式不同。

图3 烧结温度950℃下各样品的拉曼图谱Fig．3 Raman spectra of samples sintered at 950 ℃

图4 烧结温度1 080℃下各样品的拉曼图谱Fig．4 Raman spectra of samples sintered at 1 080 ℃

表1 各样品在室温测得的3个特征峰频率变化Table 1 Frequency shift of the three characteristic peaks of samples at room temperature

其中的C峰(在780 cm-1附近)由Nb-O-Mg弯曲模所引起，对应A1g活性模式。该模类似于一个自由氧八面体振动模式，与空间群为Fm3m的纳米有序微区有关，可作为B位化学有序度的有效探针[5,11]，该模式直接反应了钙钛矿结构中氧八面体的微小变化。图5所示为不同烧结温度下各样品的A1g模频率变化。从图中可以明显看到，烧结温度不同，A1g模的频率变化也不同。当烧结温度为1 080℃时，对应A1g模的频率先减小后增大；而烧结温度为950℃时，对应A1g模的频率则保持不变。A1g模的频率变化暗示，高温下，Cu1+的存在对B位化学有序度产生影响。

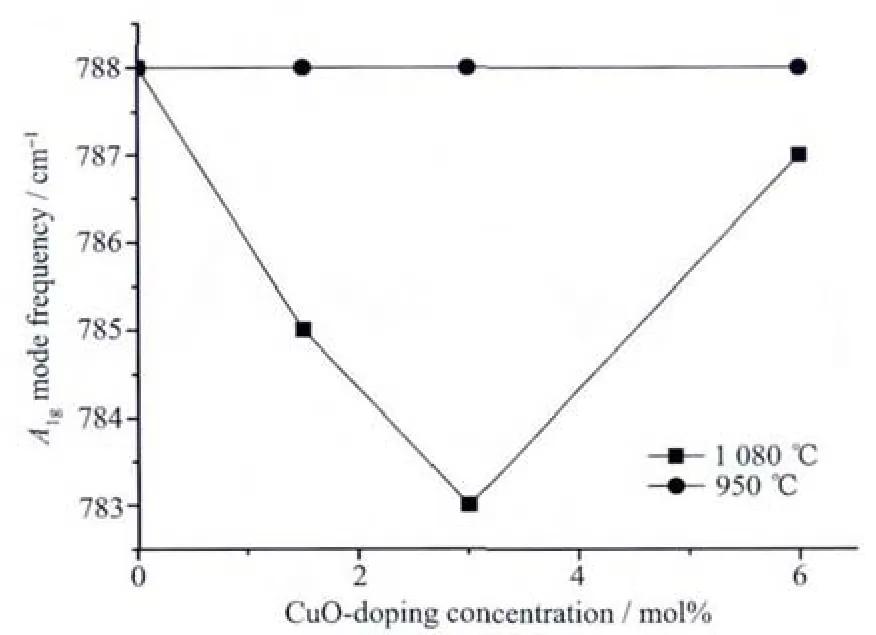
图5 不同烧结温度下对应的A1g模频率变化Fig．5 Frequency shift of the A1g mode under different sintering temperature

实验表明，化学掺杂[20]和退火热处理[21]可以改变PMN的B位离子有序度，本文使用的是化学掺杂方法。Fu等总结出用A1g模的半高宽(FWHM)来表征B位离子的有序度[5]，即A1g模的半高宽变窄对应着B位有序度的变大，其结果与HREM的分析相符合。从图3和图4中对该峰半高宽的计算后发现，950℃时，半高宽没有变化，B位有序度不发生变化；而1 080℃时，半高宽发生了变化，相应的变化值已列于表2中，那么B位化学有序度先增大后减小。可以解释为Cu2+离子进入晶格等价取代Mg2+离子，不产生电荷补偿或消弱，因而对有序度无影响；Cu+离子进入晶格不等价取代Mg2+离子，会使1∶1有序区电荷不平衡效应改变，从而改变有序度。

表2 1 080℃各样品A1g模的半高宽Table 2 Full width at half maximum of A1g mode of samples sintered at 1 080℃

有序结构的形成与弛豫铁电体的弛豫特性有很大关系，实验证明，无序态对应明显的弥散相变现象[8,22-23]。而实验中发现PMN掺La的弥散相变(DPT)的强弱难于与B位有序微区的大小简单相联系，其原因可能是A位掺杂的PMN不同于纯PST或纯PMN，前者不但有B位离子的有序问题，而且还有A位离子(可能还有掺La引起的铅空位)的有序问题，它其实是A、B位离子的有序无序结构的协同作用[24]。Cu离子进入晶格只引发B位离子有序无序结构的改变，因此，可以运用有序无序模型来解释弥散程度与有序度的关系。那么，对1 080℃的样品弥散度(δ)进行计算，计算方程[25]如下：

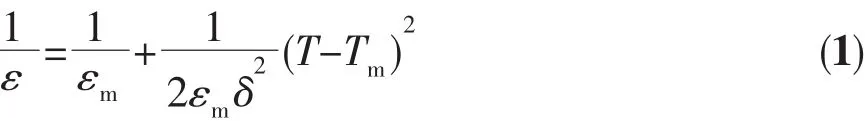
图6 1 080℃样品的介电温谱Fig．6 Temperature dependence of dielectric constant of samples sintered at 1 080℃

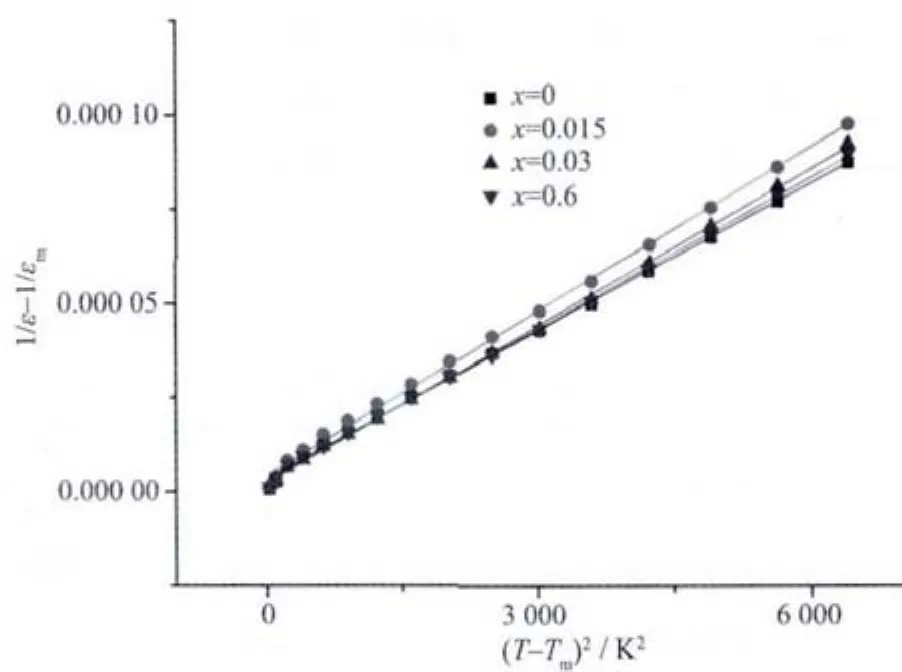
图 7 陶瓷样品的(1/ε-1/εm)～(T-T m)2线性拟合图Fig．7 Linear fitting graph of(1/ε-1/εm)～(T-T m)2

式中：ε和εm为相对介电常数及其最大值，T和Tm为ε和εm对应的温度，δ是弥散度。图6是样品烧结温度1 080℃的介电温谱。在T＞Tm的条件下，对(1/ε-1/εm)～(T-Tm)2进行线性拟合，图 7 为拟合图。由直线斜率计算得到的弥散度δ已呈现在图8中。根据有序无序模型，从图8中可以看出随着CuO掺杂量的增加弥散程度先减小后增加，表明Cu+离子的引入，使B位离子有序度先增加后减小，与拉曼光谱分析结果一致。

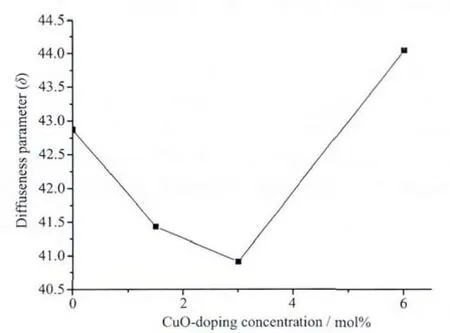
图8 各样品的弥散度Fig．8 Diffuseness parameterδof samples

3 结论

本文采用传统固相法制备铅基铁电陶瓷，研究了不同烧结温度下，添加CuO对PMN-6PT弛豫铁电陶瓷B位化学有序度的影响。拉曼和XRD分析结果表明，不同的烧结温度下，离子取代不同，对B位有序度的影响不同。烧结温度在950℃时，主要是Cu2+进入晶格，不影响化学有序度；烧结温度在1 080℃时，CuO分解为Cu2O，主要是Cu+进入晶格，有序度改变。介温测试所表现出来的弛豫特性与拉曼分析有序度的结果相一致。

[1]CHEN Xue-Feng(陈学锋),LI Hua-Mei(李华梅),LI Dong-Jie(李东杰),et al．Acta Phy.Sin.(Wuli Xuebao),2008,57(11):7298-7303

[2]Haertling G H．J.Am.Ceram.Soc.,1999,82(4):797-818

[3]Swartz SL,Shrout T R,Schulze W A,et al．J.Am.Ceram.Soc．,1984,67(5):311-314

[4]Uchino K．Am.Ceram.Soc.Bull.,1986,65:647-652

[5]YAO Wen-Long(姚文龙),FENGChu-De(冯楚德),YANG Yi(杨毅),et al．J.Inorg.Mater.(Wuji Cailiao Xuebao),2002,17(6):1181-1186

[6]Smolensky G A,Isupon V A,Agranaovska A I,et al．Soc.Phys.Solid.State．,1961,2(11):2584-2594

[7]Chen J,Chan H M,Harmer M P．J.Am.Ceram.Soc.,1989,72(4):593-598

[8]Cross L E．Ferroelectrics,1987,76(1):241-267

[9]Yao X,Chen ZL,Cross L E．J.Appl.Phys.,1983,54(6):3399-3403

[10]Akbas M A,Davis P K．J.Am.Ceram.Soc.,1997,80(11):2933-2936

[11]Fu M J,Kojima S,Zhao C,et al．Appl.Phys.Lett.,2001,79:3938-3940

[12]Lin D,Kwok K W,Chan H L W．J.Appl.Phys.,2007,90:232903