潜艇湿表面抗冲覆盖层压缩特性及抗冲击性能研究

肖 锋，华宏星，谌 勇，黄修长，朱大巍

(上海交通大学 机械系统与振动国家重点实验室，上海 200240)

潜艇关系国家安全，不仅是重要核常威慑与反击力量，亦是敌防范及打击的重点目标。潜艇由于水下作战环境恶劣，一旦发生冲击损伤极难修复，易导致灾难性后果，因此要求其具有较一般水面舰艇更高的抗冲击能力。对于潜艇尤其核潜艇而言，保存自己是第一要务。即要求潜艇在执行任务过程中具有隐蔽性、安全性、可靠性以及较好的防护与恢复能力。而防护核心在于提高潜艇的抗水下爆炸冲击能力，使其在鱼雷、水雷、深水炸弹等反潜武器攻击下仍能保持完成任务能力。提高潜艇抗冲击能力有助于其受攻击后保持原有的隐蔽性及可靠性，降低次生灾害与受二次攻击概率［1］。

在舰船湿表面敷设弹性材料防护覆盖层是提高水下非接触性抗爆性能的有效方法。研究表明，覆盖层的抗冲击性能主要取决于其内部空腔及材料。在空腔不被压实情况下，空腔越大，覆盖层抗冲击性能越好。与水面舰船不同，潜艇在水下需承受较大静水压力。虽已有消声瓦、去耦瓦声学覆盖层敷设在艇体湿表面，但抗冲效果并不理想。而目前的抗冲覆盖层均为针对水面舰船设计，国内潜艇抗冲覆盖层研究尚未展开。覆盖层抗冲击重要机理为空腔变形吸能，若将舰船抗冲覆盖层直接用于潜艇，覆盖层中空腔在强度较大静水压作用后必会发生较大压缩变形，会严重影响覆盖层的抗冲击性能［2－8］。

为解决潜艇湿表面覆盖层承压与抗冲间之矛盾，本文对六边形蜂窝抗冲覆盖层进行改进，使整个覆盖层能承受一定静水压力，当冲击波载荷作用后，覆盖层会较快发生变形吸能。为此，本文对潜艇湿表面抗冲覆盖层的准静态压缩特性及爆炸载荷作用下抗冲击性能进行研究［9－12］。讨论钢片厚度及偏距对承压特性与抗冲击性能影响。分析结果将对潜艇湿表面抗冲覆盖层设计与研究提供参考。

1 模型及材料

承压抗冲覆盖层整个单胞模型由六边形蜂窝结构与两薄钢片组成，见图1。图2为两支撑钢片。蜂窝结构材料采用邵氏硬度65氯丁胶。图3为氯丁胶单向拉压材料试验数据。钢材料弹性模量2.1E+11 Pa，泊松比0.3，密度7850 kg/m3;单胞模型长50 mm，宽5 mm，高50 mm。为讨论钢片厚度及偏距(薄片中部离Y向距离)对承压特性与抗冲击性能影响，分别取7种厚度、5 种偏距。厚度分别为 0.5 mm、0.6 mm、0.7 mm、0.8 mm、0.9 mm、1 mm、1.1 mm。偏距1 为0.554 mm，偏距2为0.754 mm，偏距3为 1.153 mm，偏距4为1.353 mm，偏距5 为1.553 mm。

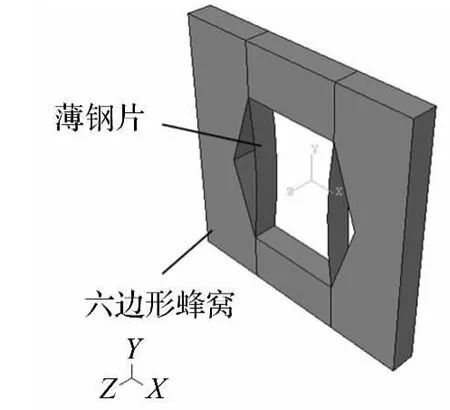
图1 覆盖层模型Fig.1 The model of the cladding

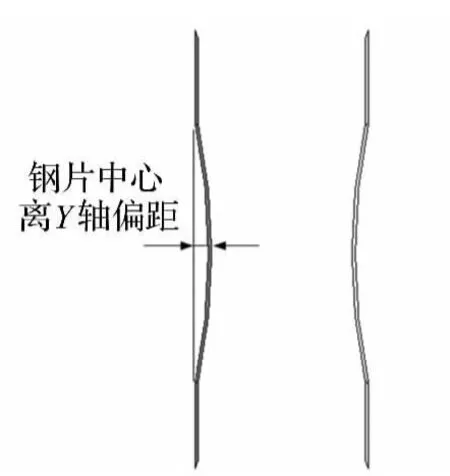
图2 支撑钢片Fig.2 Steel sheet

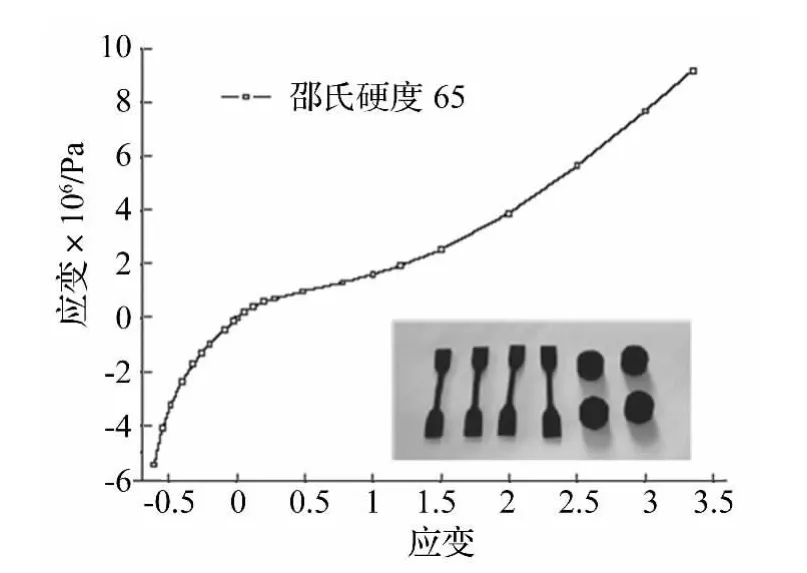
图3 邵氏硬度65氯丁胶材料试验数据Fig.3 Rubber material test data of neoprene with shore hardness number 65

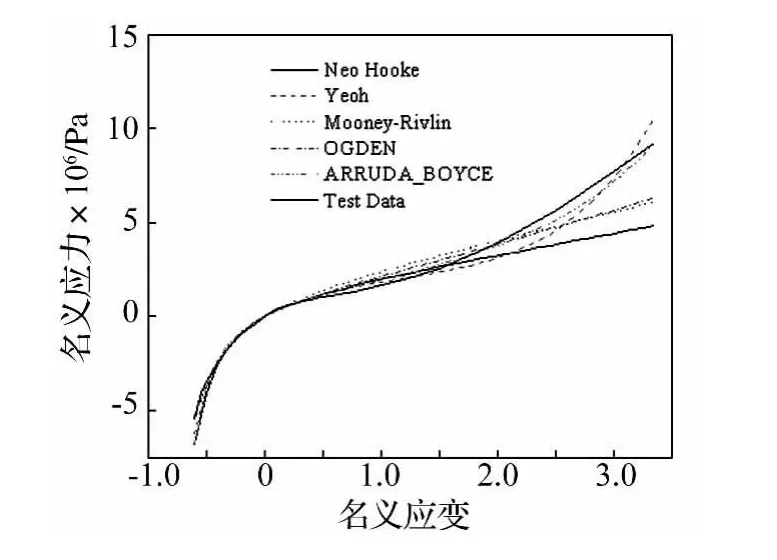
图4 拟合数据与试验数据比较曲线Fig.4 The comparison curves of fitted data and test data

基于相同测试数据，Abaqus中不同超弹性本构模型适用于不同橡胶材料、应变区间、试验方法。为此，本文选择5种常用模型对试验数据进行拟合［13］，见图4。由拟合结果看出，Mooney-Rivlin模型拟合曲线在小应变时较精确，而在中等应变及大应变时曲线趋势同试验数据差别较大。Neo-Hookean模型在预测30%～40%的中等应变单轴拉伸时拟合较好，但在预报大变形时与试验数据相差最大。两种模型因其各自应变能密度均为不变量的线性函数，故不能表示应力－应变曲线大应变部分的陡升行为。Yeoh模型在中等变形时出现软化，而在大变形情况下材料又变硬。曲线趋势较以上两种模型有所改进，但与试验数据差别仍较大。Arruda-Boyce模型在中等变形及大应变区较Yeoh模型吻合性更好，其曲线形式与试验数据拟合最好，可适用全应变范围条件。Ogden模型在中应变区较Mooney-Rivlin模型精度略高，但在大应变区优势不明显。因此，在应变不太大时Mooney-Rivlin与Ogden模型精度略高。中变形区其它3种模型精度略高，大变形区选用Arruda-Boyce模型较合理。因此，计算中均采用该模型。拟合常数MU=963 456.497，MU_0=1039813.22、LAMBDA_M=2.9193、D=3.849 4E －9，单位 Pa。

2 覆盖层准静态压缩下性能分析

因艇体重量较大，且刚度较橡胶大的多，故将覆盖层下表面固定。在蜂窝结构左右两外侧边界施加周期性对称边界条件模拟覆盖层周期性，同时限制所有面外位移。蜂窝结构用C3D8R单元划分，钢片用S4R单元划分。网格尺寸均取0.8 mm。在覆盖层上表面以均布恒速单向下压方式加载。0.1 m/s压缩下计算结果与0.01 m/s下相同，故选0.1 m/s压缩速度。为考察覆盖层压缩变形初期力学性能，总压缩量取10 mm，占覆盖层高度的20%。有无片覆盖层压缩变形瞬态图见图5。由图5看出，有片覆盖层的变形除蜂窝边向内凹外，两钢片分别向存在偏距的一侧弯曲。

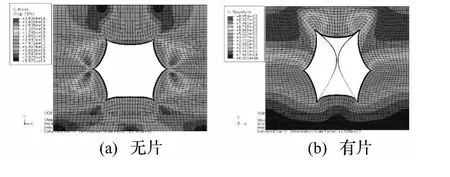
图5 覆盖层压缩变形瞬态图Fig.5 The transient deformation of the claddings

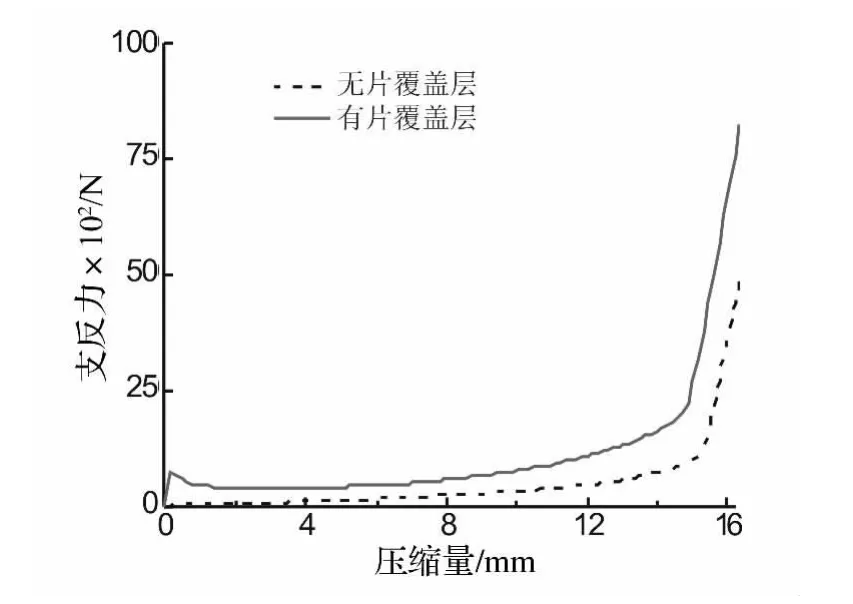
图6 覆盖层支反力－压缩量变化曲线Fig.6 The reaction force-displacement curves

2.1 覆盖层支反力－压缩量曲线分析

通过取覆盖层底端下表面所有节点在Y向支反力合力间接获得作用于艇体钢板上的力。

图6为无片支撑覆盖层与有片支撑覆盖层(片厚0.001 1 m，偏距1)支反力－压缩量变化曲线。无片覆盖层经历压缩过程两个阶段，而有片覆盖层经历压缩过程三个阶段。当压缩量约15 mm时，压缩正式进入密实化阶段。

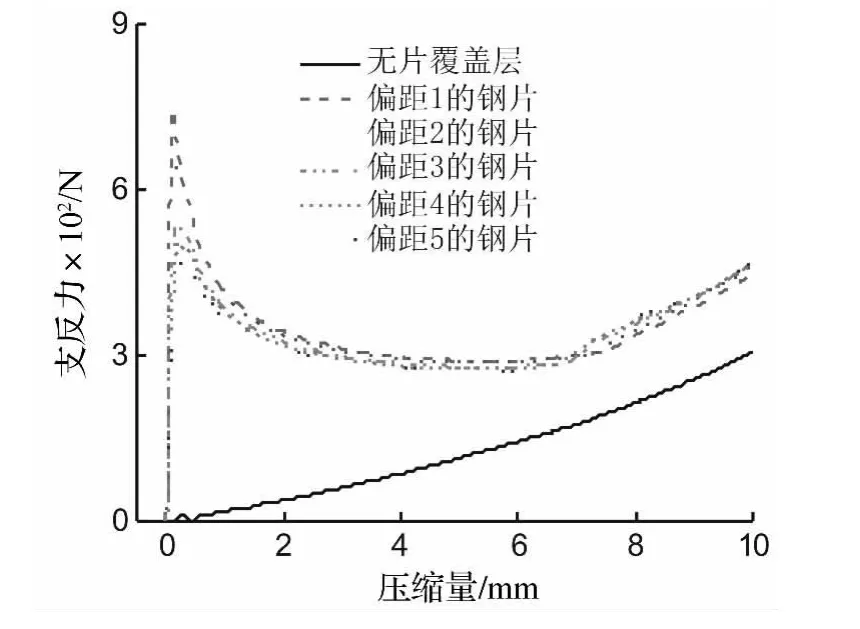
图7 钢片支反力－压缩量变化曲线Fig.7 The reaction force-displacement curves

图7为无片覆盖层及1.1mm厚度不同偏距钢片的支反力－压缩量变化曲线。由图7看出，10 mm压缩范围内，钢片支反力－压缩量曲线可分为3个阶段，即压缩初期峰值阶段、钢片弯曲与屈曲阶段、左右两钢片相互接触后挤压阶段。压缩初期初始峰值可保证模型小的初始静变形量。钢片弯曲及屈曲阶段，支反力迅速减小，钢片出现软化，表现出负刚度特性，此可提高抗冲击性能。钢片负刚度特性随偏距增大而变得不明显。钢片具有较大静承载能力的同时，又有较宽位移范围内较低动刚度。而无片支撑覆盖层支反力曲线在压缩初期呈线性增加，并无支反力初始峰值及平台。当压缩量达到7 mm左右时，无片支撑覆盖层与有钢片曲线趋势相似。整个压缩过程中，无片覆盖层支反力小于钢片支反力，说明无片覆盖层抗压能力较有片覆盖层弱，支反力相同时，无片覆盖层更易发生压缩变形。无片覆盖层支反力达到有片覆盖层相同支反力初始峰值需较大压缩量，而空腔大小会随压缩量的增加而减少，甚至空腔原形状改变，导致覆盖层力学性能降低。

图8为1 mm钢片覆盖层在不同偏距下支反力－压缩量变化曲线，由图8看出，有片覆盖层支反力曲线为无片覆盖层与钢片支反力曲线的叠加。偏距较小的覆盖层在压缩初始阶段支反力峰值明显，偏距越小，峰值越大，上升越快，且峰值时间有所提前。支反力初始峰值的出现与片厚度及偏距有关。偏距为3～5时无明显支反力峰值;偏距为1～2时出现突跃的支反力峰值。支反力初始峰值随偏距的减小而增大。峰值从大到小顺序依次为:偏距1、偏距2、偏距3、偏距4、偏距5。

图9为偏距3覆盖层不同钢片厚度下支反力－压缩量变化曲线。由图9看出，同一偏距下，随片厚度的增加，支反力初始峰值增加，且在压缩量范围内，片厚度越大，覆盖层支反力曲线越高，支反力平台长度也更长。

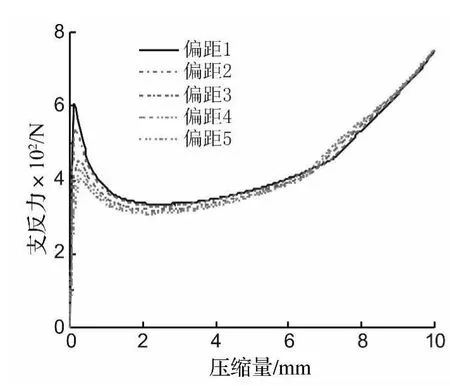
图8 覆盖层支反力－压缩量变化曲线Fig.8 The reaction force-displacement curves

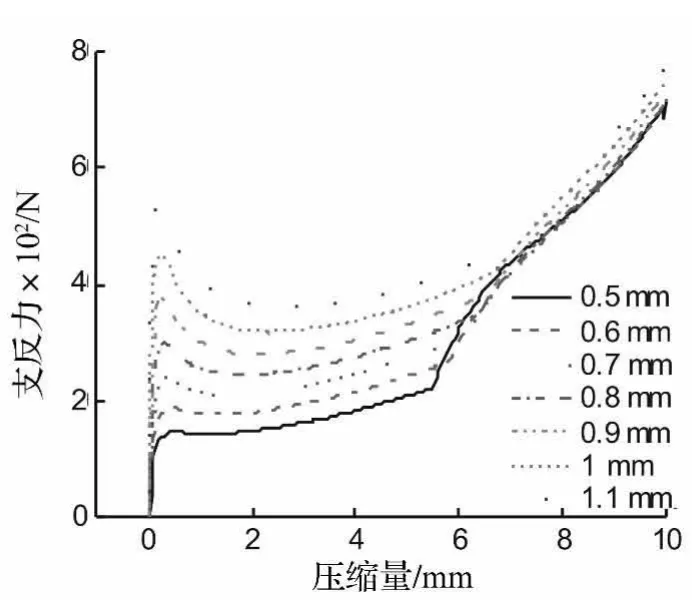
图9 钢片支反力－压缩量变化曲线Fig.9 The reaction force-displacement curves

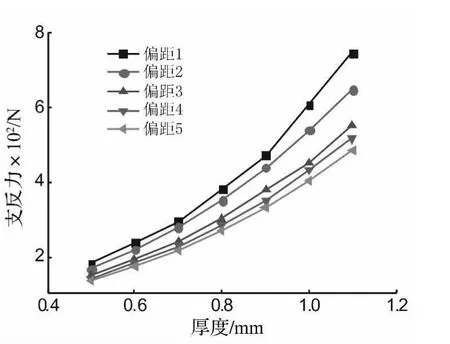
图10 支反力初始峰值曲线Fig.10 The curves of reaction force peak

2.2 支反力初始峰值及水深、压缩量、吸能量

图10为不同片厚度及偏距覆盖层的支反力初始峰值曲线。由于覆盖层能承受的静水压力与水深均与支反力初始峰值有关，因此其曲线趋势与支反力初始峰值曲线趋势一致，仅幅值不同。在同一偏距下，随片厚度的增加，支反力初始峰值、静水压力、水深逐渐上升，且片厚度越大，上升幅度越大，上升速度亦越快。而在同一片厚度下，随偏距的增加，峰值下降幅度越大。片厚度较小时，各偏距下峰值间相差较小。增加片厚度，各偏距的峰值间相差增大。在各片厚度下，不同偏距峰值大小顺序具有一致性，从大到小顺序依次为:偏距1、偏距 2、偏距3、偏距 4、偏距5。

初始峰值对应的水深见表1。片厚度0.5 mm，偏距5的覆盖层支反力初始峰值最小为134.38 N，静水压力最小为537 544 Pa，水深最小为54.85 m。片厚度为1.1 mm，偏距为1的覆盖层支反力初始峰值最大为747.98 N，静水压力峰值最大为2 991 948 Pa，水深峰值最大为305 m。

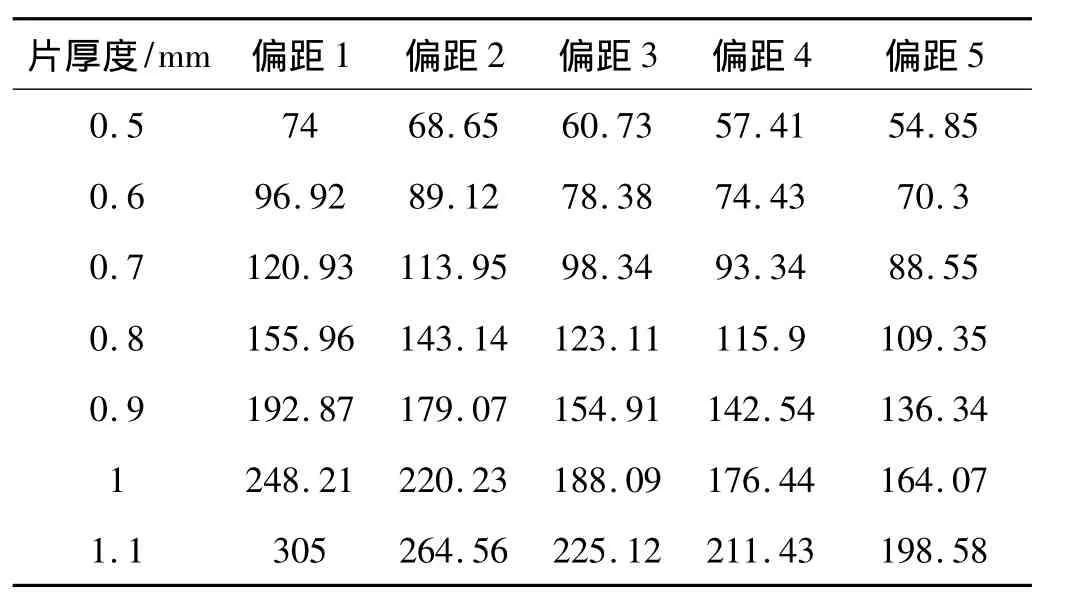
表1 水深单位(m)Tab.1 Water depth unit(m)

图11为不同片厚度及偏距下覆盖层支反力初始峰值对应的压缩量曲线。由图11看出，随片厚度的增加，各偏距下压缩量总体呈下降趋势。覆盖层偏距越大，压缩量下降幅度越大，下降速度亦越快。当厚度较小时，偏距1及偏距5对应的压缩量之间相差明显。覆盖层偏距越小，在不同厚度下支反力初始峰值对应的压缩量越小，越难压缩。由同一偏距下不同片厚度压缩量变化趋势看出，偏距为1时，随片厚度的增加，支反力初始峰值对应的压缩量先增大，后减小，再增大，再减小。偏距为2、3、4、5时，随片厚度的增加，压缩量总体趋势均减小，仅减小程度不同。由同片厚度下不同偏距压缩量变化趋势看出，随偏距的增加，压缩量逐渐增大。0.5 mm片厚度下偏距4、5的覆盖层压缩量最大，为6.500 05 mm。1 mm、1.1 mm 片厚度下偏距1的覆盖层压缩量最小，为1.000 12 mm。

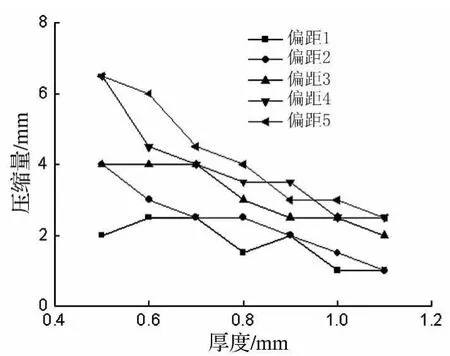
图11 压缩量曲线Fig.11 The curves of compression amount

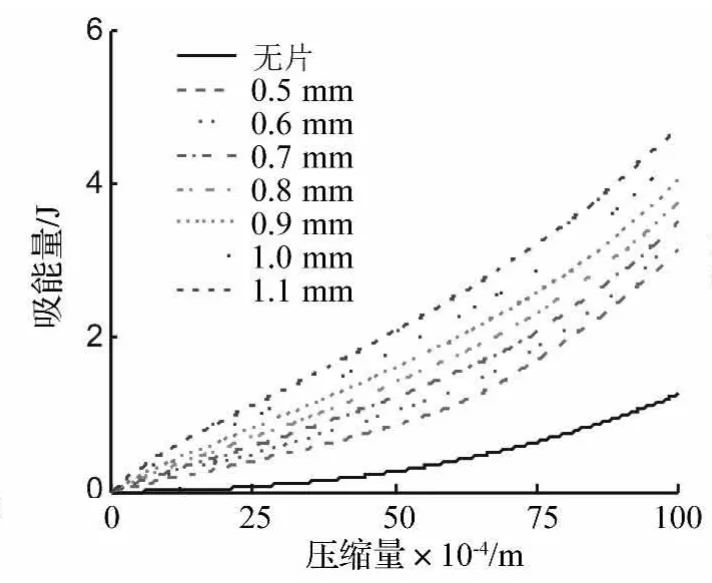
图12 吸能－压缩量变化曲线Fig.12 The absorbed energy-displacement curves

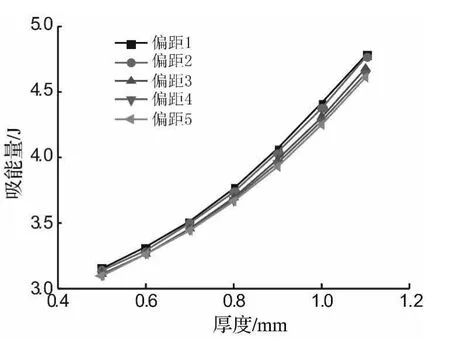
图13 吸能量曲线Fig.13 The curves of absorbed energy

压缩过程中覆盖层的变形能与动能占总能量的绝大部分，故用两者之和考察吸能量。不同片厚度下吸能－压缩量变化曲线具有相似性，图12为偏距1覆盖层不同片厚度下吸能－压缩量化曲线。由图12看出，不同片厚度下覆盖层的吸能量随压缩量的增加总体呈上降趋势，且片厚度越大覆盖层吸能量越大。当覆盖层承载时，施加其上的作用力会做功。支反力－压缩量之下的面积即为变形所需的功。正是支反力曲线上长的平台，使覆盖层出现大的能量吸收，该平台来自空穴屈曲、钢片弯曲而产生的坍塌。与支反力－压缩量变化曲线相对应，支反力－压缩量之下面积越大覆盖层吸能量也越大，而无片覆盖层支反力－压缩量曲线包围的面积最小，吸能亦最小。相同压缩量下，覆盖层吸能量越多，表明其可耗散更多的爆炸冲击能量，能承受更大强度的爆炸冲击载荷。相同吸能量，结构抗压能力越弱压缩量越大。

图13为压缩量达0.01 m时不同片厚度及偏距下覆盖层吸能量曲线。由图13看出，随片厚度的增加，不同偏距下覆盖层的吸能量总体呈上升趋势。覆盖层偏距越小，吸能越多，且随片厚度的增加，各偏距下支反力－压缩量曲线包围的面积显著增加，吸能量上升幅度更大，上降速度也越快。厚度较小时，偏距1、5对应吸能量间相差较小;厚度较大时，各偏距下吸能量间相差增大。因此，厚度对不同偏距下覆盖层的吸能影响较大。

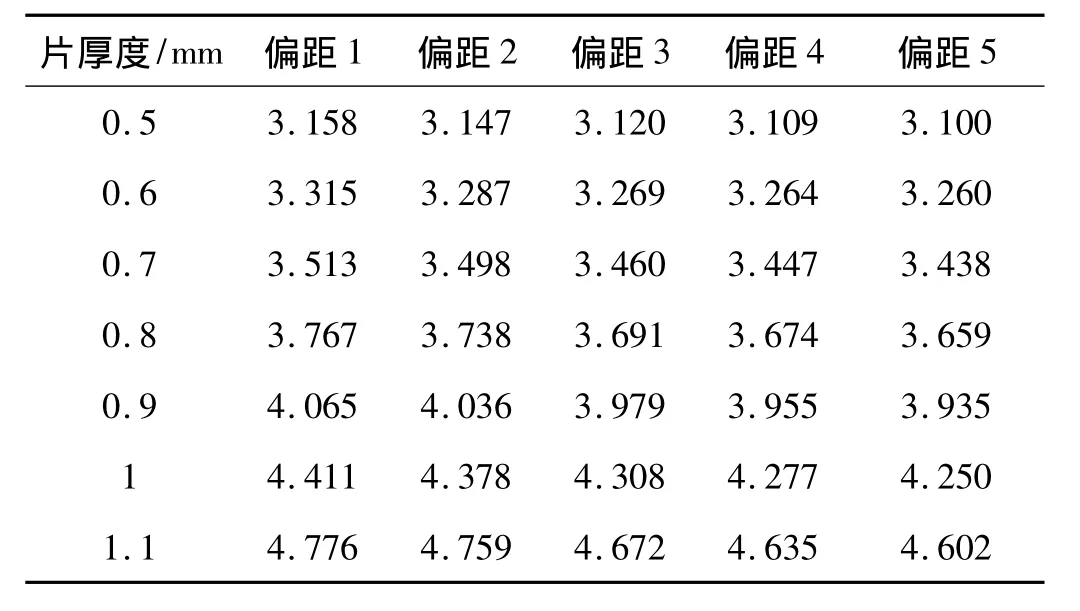
表2 覆盖层的吸能量单位(J)Tab.2 The absorbed energy of the cladding unit(J)

表2为压缩量达0.01 m时不同钢片厚度及偏距下覆盖层对应的吸能量。由表2看出，在不同钢片厚度下，随偏距的增加，吸能量逐渐减小。偏距1吸能最大，偏距5吸能较少。随片厚度的增加，吸能量间相差增大。无片覆盖层吸能量为1.267 J，远小于有片覆盖层吸能量。0.5 mm钢片及偏距5的覆盖层压缩量最大，但吸能量最小，为3.10041 J。1.1 mm钢片及偏距1的覆盖层压缩量最小，但吸能量最大，为4.77651 J。由此看出，压缩量非覆盖层支反力初始峰值对应吸能的决定因素，片厚度与偏距影响较大，片厚的与偏距小的吸能会更大。

3 爆炸冲击波载荷作用覆盖层抗冲击性能分析

覆盖层抗冲击性能主要取决于结构自身的抗冲击性能。研究表明，覆盖层变形吸能对抗冲击性能影响远大于流体及覆盖层相互作用影响。考虑到水下爆炸的复杂性，同时为更清楚了解覆盖层本身的抗冲击性能，暂不考虑流体与覆盖层的相互作用，只研究覆盖层结构自身的抗冲击性能。为探究钢片厚度、偏距与覆盖层抗冲击性能间内在关联，研究30 MPa压力幅值的水下爆炸冲击波载荷。由于气泡脉动对艇上设备产生的加速度影响较冲击波载荷小的多，故外加载荷只考虑冲击波载荷。沿用库尔经验公式，30 MPa压力峰值水下爆炸冲击波载荷－时间曲线［14］见图14。两种材料、覆盖层模型网格划分及边界条件与准静态压缩下一致。由于冲击载荷下橡胶覆盖层变形不大，且橡胶体对应变速率依赖性不强［12］，材料应变率取500 1/s［4］。钢片用Cowper-Symomds应变率强化模型，材料参数D=40，q=5。在覆盖层上表面施加爆炸冲击载荷。总爆炸响应计算时间取0.003 s。

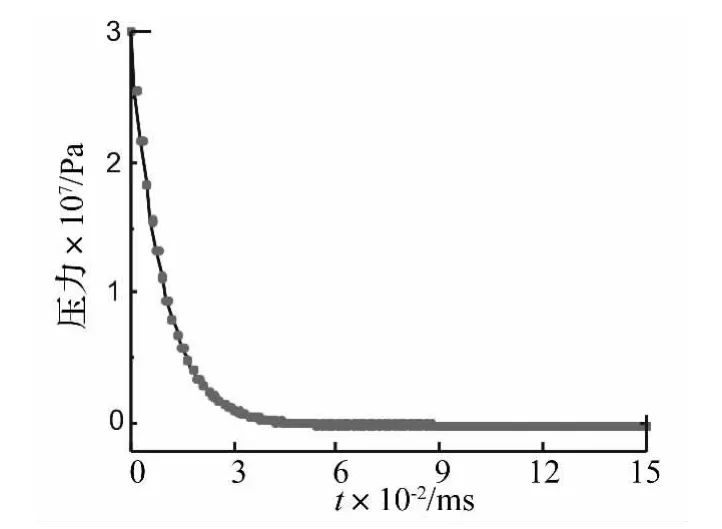
图14 爆炸冲击波载荷－时间曲线Fig.14 Blast shock wave pressure-time curve

图15为有无片覆盖层在爆炸冲击作用下的瞬态变形图。可以看出，与准静态压缩相比，覆盖层变形不匀称，主要发生在覆盖层顶部区域;两钢片分别向存在偏距的一侧弯曲。无片覆盖层顶端中间局部变形较大，有钢片覆盖层顶部中间由于钢片支撑其变形趋于总体变形。

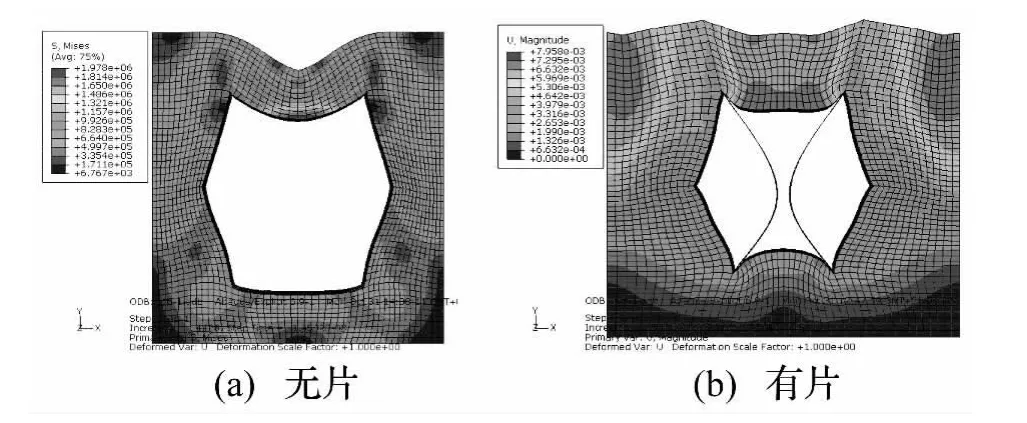
图15 覆盖层瞬态变形图Fig.15 The transient deformation of the claddings

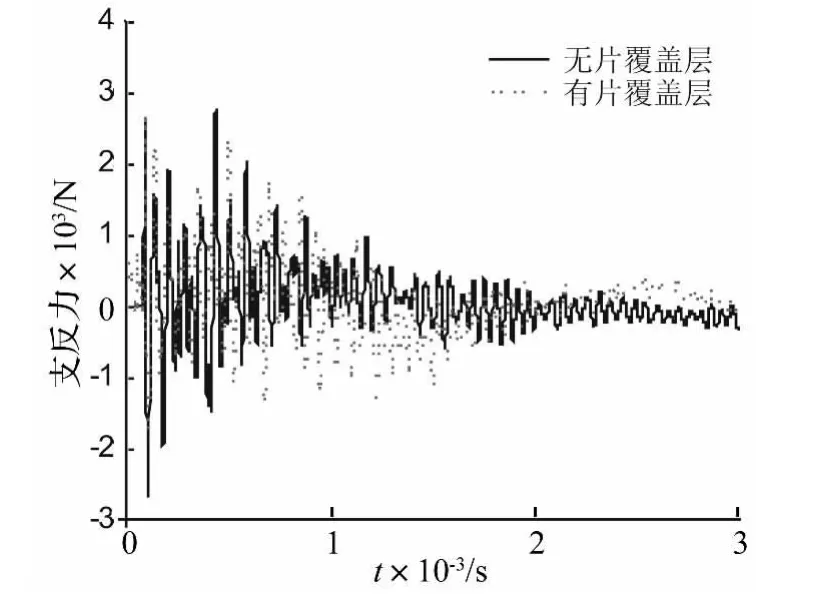
图16 覆盖层支反力时间响应比较曲线Fig.16 The reaction force curves

图16为有无片覆盖层在爆炸冲击作用下支反力时间响应比较曲线。可以看出，两者支反力曲线趋势相近，均先有一较大初始峰值，之后来回振荡衰减，后期衰减较快，区别在于两者支反力初始峰值大小有所改变。

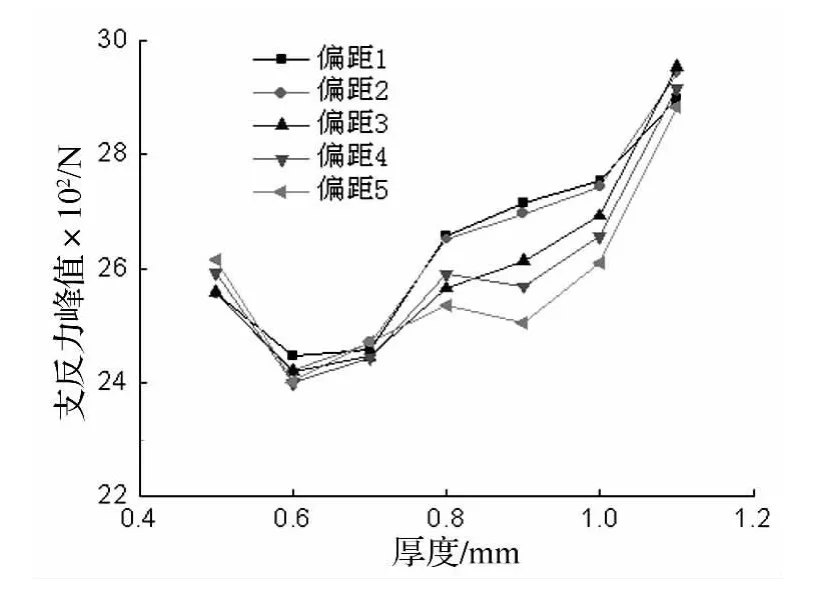
图17 支反力峰值曲线Fig.17 The curves of reaction force peak

图17为不同片厚度及偏距下覆盖层的支反力峰值曲线。由图17看出，不同偏距下覆盖层支反力峰值曲线总体变化趋势较一致，峰值均有先减小后增大现象。由于支撑钢片由三段组成，因此覆盖层抗冲击性能为其共同作用结果。此变化规律并非简单的线性关系:片厚度从0.5 mm变化到0.8 mm时，各偏距下支反力峰值先减小后增大;片厚度从0.8 mm变化到1.1 mm时，偏距4、5下峰值均先减少后增大;而偏距1、2、3的峰值均逐渐上升。片厚度 0.5 mm、0.6 mm、0.7 mm及1.1 mm时，各偏距下峰值接近。片厚度0.8 mm、0.9 mm、1.0 mm 时，各偏距下峰值相差明显，且片厚度为0.9 mm时，各偏距下峰值相差最明显。

表3为不同片厚度及偏距下覆盖层支反力峰值。片厚度0.5 mm时，偏距2的支反力峰值最小，偏距5的支反力峰值最大;片厚度0.6 mm时，偏距4的支反力峰值最小，偏距1的峰值最大;片厚度0.7 mm时，偏距4的峰值最小，偏距5的峰值最大;片厚度0.8 mm时，偏距5的峰值最小，偏距1的峰值最大;片厚度0.9 mm时，偏距5的峰值最小，偏距1的峰值最大;片厚度1 mm时，偏距5的峰值最小，偏距1的峰值最大;片厚度1.1 mm时，偏距5的峰值最小，偏距3的峰值最大。由此，随着厚度的增加，偏距大的支反力峰值较小。无片覆盖层支反力峰值为2 635.3 N。有片支撑覆盖层除厚度 0.8 mm、0.9 mm 下偏距1、2 的覆盖层，1 mm 下偏距1、2、3、4的覆盖层及1.1 mm下各偏距的覆盖层，其支反力峰值均较小。

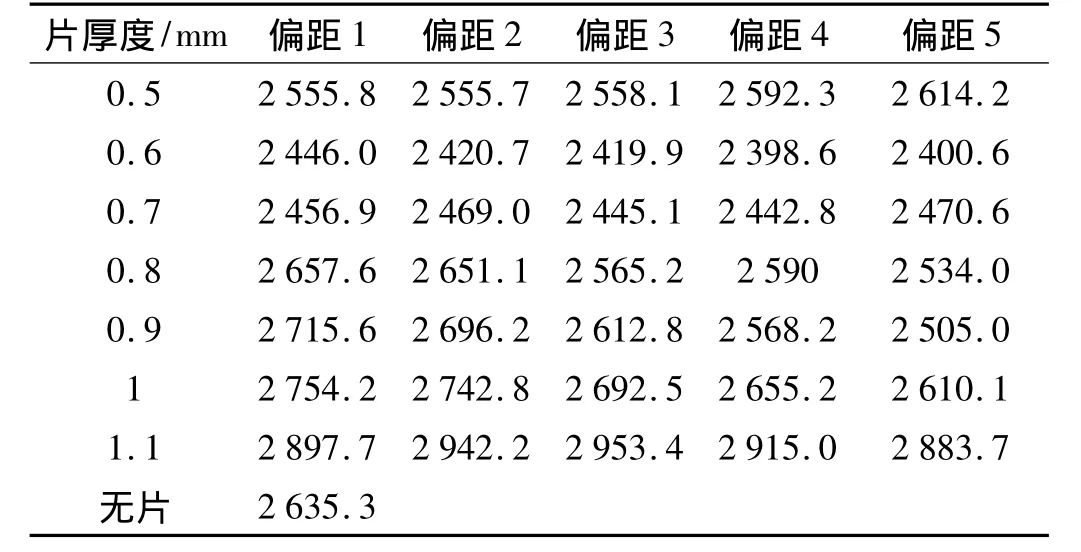
表3 支反力峰值单位(N)Tab.3 Reaction force peak unit(N)

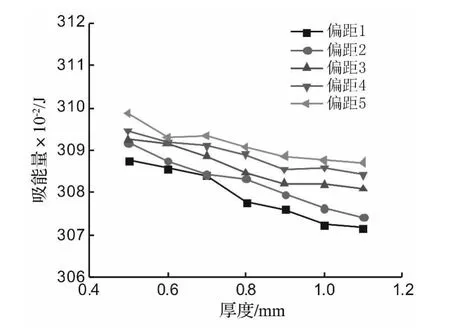
图18 吸能量曲线Fig.18 The curves of absorbed energy

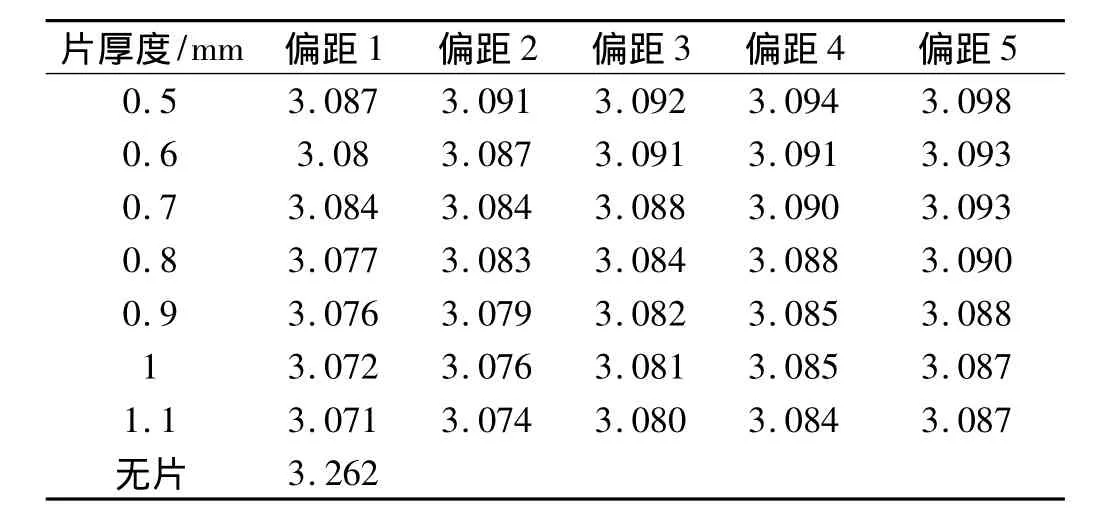
表4 吸能量单位(J)Tab.4 Absorbed energy unit(J)

图18为不同片厚度及偏距下覆盖层支反力峰值对应的吸能曲线。由图18看出，随片厚度的增加，各偏距下覆盖层的吸能量不断减小，吸能量间相差逐渐增多。对各片厚度的覆盖层，随偏距的增加，吸能量逐渐增大。各片厚度下覆盖层的吸能量从大到小顺序依次为:偏距5、偏距4、偏距3、偏距2、偏距1。

表4为不同片厚度及偏距下覆盖层支反力峰值对应的吸能量。无片覆盖层吸能量为3.262 J。有片支撑的覆盖层支反力峰值对应的吸能量均较无片支撑覆盖层小。从片厚度对同一偏距下覆盖层吸能量影响角度看，对偏距1、2、3的覆盖层，随片厚度的增加，支反力峰值对应的吸能量不断减小。对偏距4、5，随片厚度的增加，吸能量先减小后增大再减小。从偏距对同一片厚度下覆盖层吸能量影响角度看，随偏距的增加，吸能量逐渐增大。

4 结论

(1)纵观准静态压缩下覆盖层力学特性，无片支撑覆盖层支反力曲线在压缩初期支反力呈线性增加，并无支反力初始峰值及支反力平台，不利于深水下承受高静水压力。在覆盖层空腔中加入钢片支撑后，支反力曲线出现明显支反力初始峰值与支反力平台，使整个覆盖层的吸能量增多，会提高覆盖层的承压性能。片厚度越小且偏距越大，覆盖层所能承受的水深越浅，且支反力初始峰值对应的压缩量越大。在同一偏距下，随钢片厚度的增加，支反力初始峰值、静水压力、水深逐渐上升，且钢片厚度越大，上升越高，上升速度越快。厚度较小时，各偏距下峰值间相差较小。在同一钢片厚度下，随偏距的增加，峰值下降越大。随钢片厚度的增加，各偏距下峰值间相差增大。在整个压缩量范围内，同一偏距下各覆盖层的吸能量随压缩量的增加总体呈上降趋势而增加，且钢片厚度越大覆盖层吸能量越大。同一钢片厚度下，随偏距的增加，吸能量先减小后增大，再减小。

(2)观察冲击载荷作用下覆盖层的抗冲性能，有片支撑覆盖层中片厚度越厚且偏距越小，其支反力峰值越会大于无片支撑覆盖层峰值。而有片支撑的覆盖层支反力峰值对应的吸能量均较无片支撑覆盖层小。支反力峰值出现在偏距大的覆盖层中。0.6 mm厚度、偏距4的覆盖层峰值最小，其能承受的水深为74.43 m，换算到静水压力为729 452 Pa。1.1 mm厚度、偏距3的覆盖层峰值最大，其能承受的水深为225.12 m，换算到静水压力为2 206 136 Pa。

［1］汪 玉.实船水下爆炸冲击试验及防护技术［M］.北京:国防工业出版社，2010.

［2］姚熊亮，于秀波，庞福振，等.敷设声学覆盖层的板架结构抗冲击性能数值计算研究［J］.工程力学，2007，24(11):164－171.YAO Xiong-liang， YU Xiu-bo， PANG Fu-zhen，etal.Numerical research on the anti-shock capability of plate-frame structure coated with acoustic covering layer ［J］.Engineering Mechanics，2007，24(11):164 －171.

［3］庞福振，姚熊亮.声学覆盖层对潜艇抗水下爆炸能力的影响研究［J］.振动与冲击，2011，30(4):103－108.PANG Fu-zhen，YAO Xiong-liang.Influence of acoustic tiles on anti-underwater explosion capability of a submarine［J］.Journal of Vibration and Shock，2011，30(4):103 －108.

［4］Chen Y，Zhang Z Y，Wang Y，et al.Crush dynamics of squarehoneycomb thin rubber wall［J］. Thin-Wall Structures，2009，47(12):1447 －1456.

［5］Chen Y， ZhangZ Y， WangY， etal. Attenuating performance of a polymer layer coated onto floating structures subjected to water blasts［J］.European Journal of Mechanics A/Solids，2009，28(3):591 －598.

［6］谌 勇，华宏星，汪 玉，等.超弹性夹芯覆盖层的水下爆炸防护性能［J］.爆炸与冲击，2009，29(4):395 －400.CHEN Yong，HUA Hong-xing，WANG Yu，et al.Protective effects of hyper elastic sandwiches coated onto metal boxes subjected to underwater explosion［J］.Explosion and Shock Waves，2009，29(4):395 －400.

［7］Deshpande V S，Fleck N A.One-dimensional response of sandwich plates to underwater shock loading［J］.Journal of the Mechanics and Physics of Solids，2005，53(11):2347－2383.

［8］Chien C.Computational studies of pleurae coated steel plate under loads［C］.9th US National Congress on Computational Mechanics，San Francisco，CA，2007.

［9］Park S T，Luu T T.Techniques for optimizing parameters of negative stiffness［J］.Journal of Mechanical Engineering Science，2007，221(5):505－511.

［10］纪 晗，熊世树，袁 涌，等.基于负刚度原理的结构减震效果理论分析［J］.振动与冲击，2010，29(3):91 －94.JI Han，XIONG Shi-shu，YUAN Yong，et al. Influence analysis of the structural seismic reduction effect based on negative stiffness principle［J］.Journal of Vibration and Shock，2010，29(3):91－94.

［11］胡光军，周生通，李鸿光.一种非线性隔振器的静力分析与实验研究［J］.噪声与振动控制，2011，6:69－73.HU Guang-jun，ZHOU Sheng-tong，LI Hong-guang.Static analysis and experiment of a nonlinear vibration isolator［J］.Noise and Vibration Control，2011，6:69 －73.

［12］Gibson L J，Ashby M F.Cellular solids:structure and properties(2nd ed)［M］.Cambridge:Cambridge University Press，1997.

［13］庄 茁，由小川，廖剑晖，等.ABAQUS的有限元分析和应用［M］.北京:清华大学出版社，2009.

［14］库尔P，著.罗耀杰，韩润泽，官 信，译.水下爆炸［M］.北京:国防工业出版社，1960.