利用微分算子增强EMD算法频带分解能力

刘海波，玄志武

(91550部队94分队，辽宁 大连 116023)

Hilbert-Huang变换［1］为对非平稳、非线性信号进行分析的有效方法，且具有自适应特点，能揭示非平稳信号的局部特性，已广泛应用于机械故障检测［2-3］、结构识别［4］、外弹道去噪［5］等领域。但由于 EMD 分解由实践中总结而来，理论基础尚不完善。实际应用中难以避免出现模态混叠现象，即一个IMF分量中包含不同时间尺度组分情况，削弱了EMD算法的频带分解能力，导致分解出的本征模态函数失去原有物理意义。

Li等［6］用小波对信号进行预处理，滤除高频间断事件，一定程度上改善了分解结果，但小波基的选择需人工干预，削弱了EMD最突出的自适应性特点。Ryan等［7］在EMD分解前加入掩膜信号，对区分频率较接近的频带有一定效果，但选取掩膜信号需信号的先验信息，影响EMD算法的自适应性。

本文提出改进的EMD算法，先将提高原始信号频带分解能力的微分信号进行EMD分解，再将所得IMFs进行积分处理获得原始信号有效IMFs。仿真计算与实际工程应用表明，该方法优于传统的EMD算法，可有效分离频率较接近的本征模态函数，增强EMD方法的频带分解能力。

1 EMD方法频带分解能力

Rilling等［8］对EMD算法的信号频带分解能力给出初步解答。Feldman［9］从理论层面进行深入研究得出，假设两不同频带信号为s1，s2，其振幅与频率分别为A1，A2与f1，f2，以频率比f2/f1为横坐标，振幅比A2/A1为纵坐标，得EMD算法频带分解能力见图1。图1中，1区表示A2/A1≤(f2/f1)-2，或f2/f1≤1.5无法用EMD算法进行分解;2 区表示(f2/f1)-2≤A2/A1≤2.4(f2/f1)-1.75，需几次平移迭代才能将信号分解;3区表示A2/A1≥2.4(f2/f1)-1.75，一次迭代即能将信号分解。

由上述得，EMD算法的频带分解能力与信号振幅比A2/A1及频率比f2/f1有关。若能提高信号的振幅比，使其从1区进入2区或3区，则可用EMD进行频带分解。

图1 EMD算法频带分解能力Fig.1 Frequency decomposition ability of EMD

2 利用微分算子增强EMD频带分解能力

设输入信号x(t)由两种模态构成，即:

其中:f2＞f1，A2＜A1。信号振幅比y1可表示为:

对式(1)两边进行一阶微分得:

其振幅比为:

由于f2＞f1故y2＞y1，即通过微分增大信号振幅比，可将1区部分信号“提升”到2区或3区(如图1中箭头所示)，增强应用EMD算法进行频带分解能力，图1演化为图2。

图2 经微分算子处理的EMD频带分解能力Fig.2 Frequency decomposition ability of EMD after differentiation

图2中，① 区表示A2/A1≤(f2/f1)-3，或f2/f1≤1.5无法用微分算子处理后EMD算法将其分解;② 区表示(f2/f1)-3≤A2/A1≤2.4(f2/f1)-2.75，需几次平移迭代，才能用微分算子处理后的EMD将信号分解;③区表示A2/A1≥2.4(f2/f1)-2.75，一次迭代即能用微分算子处理后EMD算法将信号分解。

图2与图1相比，①区部分显著变小，说明EMD分解的盲区减小，即EMD的频带分解能力得以增强。

3 频带分解能力判定指标

为定量分析EMD算法的频带分解能力，引入指标Error，表示原始信号成分与分解结果间在时域上的误差:

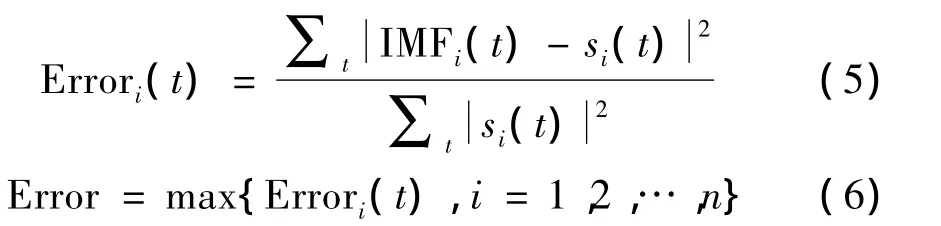
其中:IMFi(t)表示第i阶固有模态函数，n为EMD分解阶数。

对同一待分解信号，采用不同分解模式，当Error趋于0时，说明本征函数IMFi(t)与信号si(t)较接近，频带分解正确。

4 改进的EMD算法

实际工程应用中，可用差分方法代替微分过程，用累积求和方法代替积分过程。再次用EMD方法提取出累积求和后信号的高频部分作为新的IMF，避免由替代方法所致误差，而使累积求和后信号包络均值不为零的情况发生。

图3 算法流程图Fig.3 Algorithm flowchart

5 仿真分析

正弦合成信号为:

采样个数 210，图 4(a)为s(t)高频部分 0.2 sin(4πt)，图4(b)为s(t)低频部分 sin(2πt)。s(t)振幅比A2/A1=0.2，频率比f2/f1=2，因此A2/A1≤(f2/f1)-2，即图1中信号s(t)处于1区，无法用EMD算法分离频带，已由图 5结果得以证实，此时 Error为24.88。

对s(t)微分得:

工程应用中，信号往往含噪声信息，直接进行微分处理会扩大噪声，影响信号分解效果。当信噪比WS-NR为8.12时，信号s(t)经微分再经EMD分解的结果见图8。对图8各频带积分结果见图9。图8第三、四频带与图6相似;图9第三、四频带与图7相似但存差异，说明信号s(t)中加入噪声会对改进的EMD分解算法产生影响。

为进一步考察叠加噪声的强度对算法影响，在合成信号s(t)中叠加不同强度白噪声，利用本文改进的EMD算法进行处理。结果见表1，其中 WSNR表示s(t)叠加白噪声后的信噪比。信噪比由13.64降到2.89低4/5，而 Error只增加2.4倍，说明该算法对噪声适应性较好。

表1 叠加不同强度噪声对算法结果影响Tab.1 Different noise strength influence on result

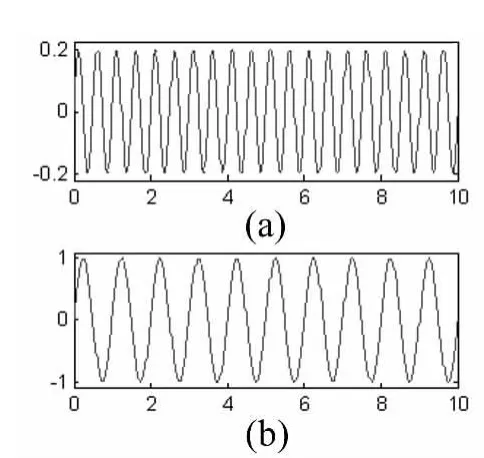
图4 信号高低频部分Fig.4 High and low frequency of the signal

图5 直接EMD分解Fig.5 EMD decomposition directly

图6 EMD微分后Fig.6 EMD decomposition after differentiation

图7 积分Fig.7 Integration

图8 加入噪声的信号经微分再经EMD分解Fig.8 EMD after noising signal differentiation

图9 图8频带积分Fig.9 Frequencies Integration on figure

6 工程应用

由于受日、月等天体影响，地球自转不规律导致地球定向参数存在多种短、长周期变化。以分析地球定向参数测量数据［10］频带周期性规律为例，检验本文算法的有效性。

图10 日长变化数据前4 096点Fig.10 First 4 096 points of LOD data

地球定向参数space2000_midnight.eop中的 LOD(length of day:日长变化)数据，记录了从1976年9月28日至2001年1月6日共8 867个数据点。取前4 096点(图10)进行EMD分解，结果见图11。IFM1～IFM7每阶固有模态函数均有不同振荡周期，代表岁差、章动、极移等因素对LOD影响。

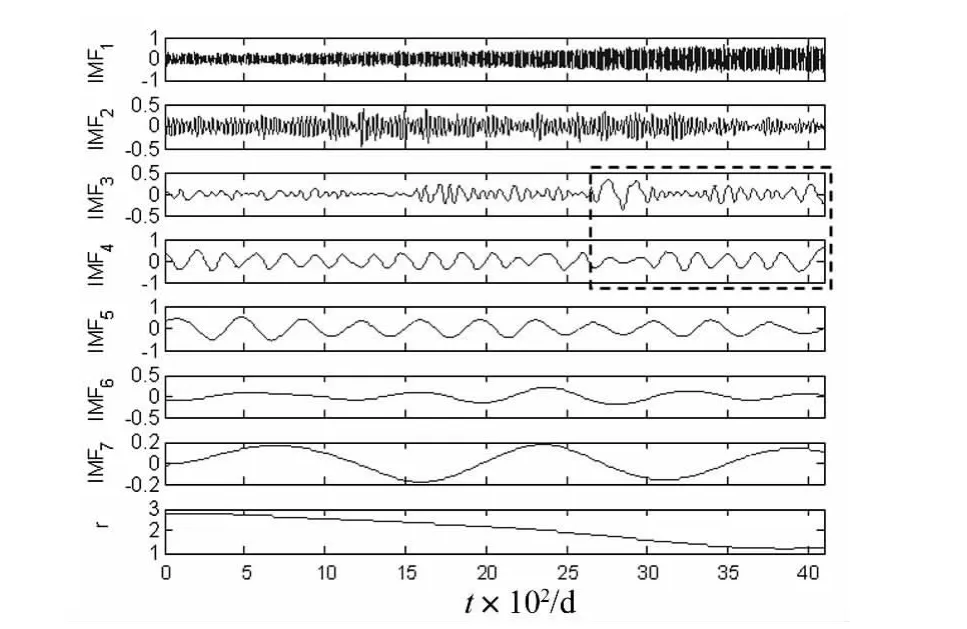
图11 LOD数据EMD分解结果Fig.11 EMD Result of LOD data

图12 用本文算法重新分解LOD数据Fig.12 Decomposition again using new method

由图11虚线方框看出，IFM5中至少包含两种尺度分量，并出现模态混叠现象，使IFM4亦受到影响。用本文改进的EMD算法重新对LOD数据进行分解，结果见图12。与图11虚线框内对比看出，该算法将原混叠模态成功分离，使各阶IMF周期规律更明显:IFM1为半月周期，IFM2为整月周期，IFM3为季度周期，IFM4为半年周期，IFM5为整年周期等。

7 结论

由仿真分析与实际工程应用得出，本文所提算法可增强EMD频带分解能力。当满足(f2/f1)-3≤A2/A1，且f2/f1＞1.5条件时，可成功对混叠模态进行频带分解。

［1］ Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proceedings of the Royal Society of London，1998，454(1971):903-995.

［2］沈 路，杨富春，周晓军，等.基于改进 EMD与形态滤波的齿轮故障特征提取［J］.振动与冲击，2010，29(3):154-157.

SHEN Lu，YANG Fu-chun，ZHOU Xiao-jun，et al.Gear faultfeature extraction based on improved EMD and morphological filter［J］.Journal of Vibration and Shock，2010，29(3):154-157.

［3］李 慧，刘小峰，夏雨峰.基于谐波小波包变换的齿轮箱包络解调分析［J］.振动与冲击，2012，31(12):129-134.

LI Hui，LIU Xiao-feng，XIA Yu-feng.A method of modal parameters identification using ambient vibration measurements for a large-scale bridge［J］. Journal of Vibration and Shock，2012，31(12):129-134.

［4］付 春，姜绍飞，杜 权.基于改进EMD的结构模态参数识别方法［J］.武汉理工大学学报，2010，32(9):280-285.

FU Chun，JIANG Shao-fei，DU Quan.Structural modal parameters identification method based on improved EMD［J］.Journal of Wuhan University of Technology，2010，32(9):280-285.

［5］郭小红，徐小辉，赵树强.基于经验模态分解的外弹道降噪方法及应用［J］.宇航学报，2008，29(4):1272-1275.

GUO Xiao-hong，XU Xiao-hui，ZHAO Shu-qiang.Noising reduction algorithm based on empirical mode decomposition(EMD)and applicationsin calculating trajectoriesof spacecraft［J］.Journal of Astronautics，2008，29(4):1272-1275.

［6］Li H，Yang L，Huang D.The study of the intermittency test filtering character of Hilbert-Huang transform ［J］.Mathematics and Computers in Simulation，2005，70:22-32.

［7］ Deering R，Kaiser J F.The use of a masking signal to improve empirical mode decomposition［C］.Philadelphia，PA，USA:Proc. of IEEE International Conference on Acoustics，Speech，and Signal Processing，2005.

［8］ Rilling G，Flandrin P.One or two frequency the empirical mode decomposition answers［J］.IEEE Transaction on Signal Processing，2008，56(1):85-95.

［9］Feldman M.Analytical basis of the EMD:two harmonics decomposition［J］. Mechanical Systems and Signals Processing，2009，23(7):2059-2071.

［10］ Gross R S.Combinations of earth orientation measurements:SPACE2000，COMB2000，and POLE2000［M］.California:JPL Publication，2001.