复合材料薄壁加筋板的压缩后屈曲研究

郑亚雄，陈 静，赵小全

(1.中国直升机设计研究所，江西景德镇 333001;2.陆航驻景德镇地区军事代表室，江西 景德镇 333001)

0 引言

复合材料加筋板壳结构大量应用于飞行器中。对大多数的实际结构，在受载时会进入非线性弯曲变形阶段，可能出现极值型屈曲和相继的后屈曲变形，因此具有可观的后屈曲承载能力［1］。目前国内外的设计准则大都规定，对于主承力结构在设计载荷下不允许发生总体和局部失稳，对于次承力结构在设计载荷下不允许发生总体失稳，在使用载荷下不允许发生局部失稳［2，3］。这一设计原则偏于保守，因此国外的航空航天研究机构开展了相关的研究工作，试图提高复合材料结构稳定性的许用值［3］。

在设计中要利用后屈曲强度特性来提高板的承载能力，就需要进行极限强度分析。对于后屈曲问题的求解方法可分为解析法和数值法两大类。解析法大都基于Koiter的初始后屈曲理论［4］，即对分支点附近的邻域根据势能驻值原理和稳定性的能量准则确定结构的分支点附近平衡状态的渐近解。这类方法作为渐近理论只能分析分支点附近的平衡状态，而不能分析大范围的后屈曲行为和较大的初始缺陷影响。因此近年来，国内外对后屈曲的相关分析多数基于非线性有限元分析进行，采用的工具包括 ANSYS、ABAQUS 和 MSC.Marc等。Chai等［5］应用ANSYS分析了层合板的后屈曲行为并利用子模型技术分析了细节应力。Orifici等［6］应用 MSC.Marc首先进行结构后屈曲分析，然后对节线和反节线建立局部模型分析加筋板的失效形式。Oh等［7］应用ABAQUS对加筋圆柱壳的后屈曲进行了分析，对不同分析方法、单元和失效准则进行了比较。刘从玉、孔斌等人［8，9］应用 ABAQUS中的界面单元模拟了筋条与面板之间的脱粘失效，结果表明考虑脱粘计算得到的极限强度更接近试验值，而不考虑脱粘得到的极限强度偏低。这些试验和模拟工作都针对壁板和筋条较厚的情况，而当壁板和筋条较薄时，由于试件的制造缺陷、边界条件与有限元模型不严格符合，以及轴压载荷分布不均匀等因素，导致试验与分析得到的变形路径差别较大［10］。付新卫等［11］对剪切稳定性试验中夹具的影响作了分析，结果表明在有限元模型中考虑夹具的影响后屈曲载荷与试验更为接近，但没有分析压缩的情况，对后屈曲也没有作进一步分析。

在直升机结构当中，复合材料大多为铺层数少的薄壁结构，对这些结构后屈曲分析的结果与试验有很大差别。并且在工程设计中，对各种结构都建立包含各种失效形式的细节模型进行分析的做法不现实。针对这一问题，本文在借鉴国内外有关研究成果的基础上，结合相关试验，采用非线性有限元方法对复合材料薄壁加筋板的轴压屈曲和后屈曲过程进行了模拟，并考虑了不同分析参数的影响，以确定对薄壁加筋板后屈曲较为合理且相对简化的分析方法。

1 压缩试验设计与初始屈曲载荷分析

1.1 压缩试验设计

试验件结构如图1所示。试件大小260mm×400mm，筋条长度为300mm，底部粘结区宽度为40mm，高度为 20mm，间距为 100mm，试验区为240mm×310mm，上下预留40mm为加强段。筋条端部按45°角切削。试件面板的铺层为［(±45°)/s，筋条铺层为［( ± 45°)/0°/加强段铺层为［(± 45°)/(0°，90°)/其中(± 45°)和(0°，90°)铺层为双向布，0°铺层为单向带。

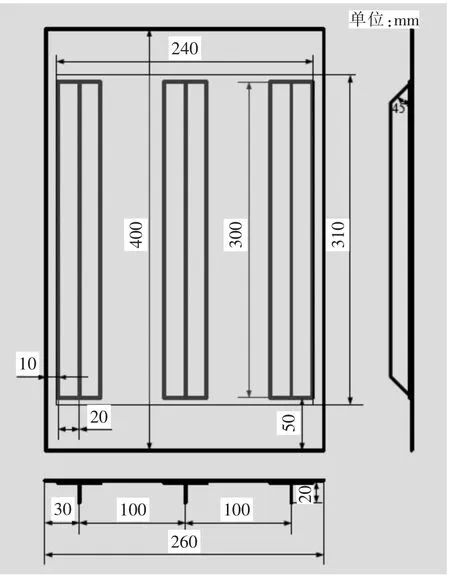
图1 压缩试验件结构尺寸图

1.2 初始屈曲载荷分析

为确定试验的加载载荷，需要对试验件的初始屈曲载荷进行分析。在实际结构设计中，作为一种保守的做法，复合材料加筋板通常按照屈曲设计。即使是按后屈曲板设计，也需要按不同的载荷组合和边界条件精确地计算出屈曲载荷。

计算初始屈曲载荷时，通常把加筋板简化成理想边界条件的正交各向异性平板，再按理论公式计算;或通过有限元模型计算。这些方法对结构都有着不同的简化。为评估这些简化对薄壁加筋板的合理性，本文对不同的方法计算得到的屈曲载荷进行比较，以确定初步设计时的简化计算原则。

使用理论计算确定加筋板的初始屈曲载荷时，需要对总体失稳载荷和局部失稳载荷分别进行计算。由于试验加载边的边界条件实际介于简支和固支之间，因此分别对两种加载边界条件进行计算，以确定初始屈曲载荷的范围。

选择不同的边界条件，计算得到加筋板的总体屈曲载荷如表1所示。

表1 总体屈曲载荷的理论计算

在计算局部局曲载荷时，腹板的等效宽度有取筋条中心间距和筋条净间距(即筋条中心间距减去筋条宽度)的不同处理方法。根据理论公式［13］，选择不同腹板等效宽度和边界条件，计算得到加筋板的初始屈曲载荷如表2所示。

表2 初始局部屈曲载荷的理论计算

计算结果表明，腹板等效宽度取筋条中心间距和筋条净间距得到的计算结果有明显差别，实际结构的屈曲载荷应处于两者之间。

同时，屈曲问题一般可以转化为数学上标准的特征值问题求解，因此可以使用有限元方法计算。用与理论计算相比，有限元计算可以更精确地模拟实际的结构和边界条件，从而可以求解比较复杂的问题。

对屈曲问题的有限元计算分为线性屈曲和非线性屈曲两类。为比较线性屈曲和非线性屈曲的结果，使用非线性有限元软件MSC.Marc进行计算。采用四节点减缩积分层合厚壳元建立有限元模型。边界条件为试验区四边以及试验件两端约束法向位移;试验件底部约束纵向位移;试验件顶部通过均布载荷加载，如图2所示，计算结构的初始屈曲载荷。对筋条与面板粘接处单元分别按加以偏置处理和无偏置进行计算。

计算得到的初始屈曲载荷如表3所示。计算得到的非线性屈曲载荷明显小于线性屈曲载荷;单元偏置对非线性屈曲载荷有明显的影响，而对线性屈曲载荷的影响相对较小。

计算得到的变形和初始屈曲模态如图3所示。由图中可见在线性模式和非线性模式下计算得到的屈曲模态有明显不同。通过屈曲模态和屈曲载荷与理论计算值的比较可以发现，使用理论公式计算局部屈曲载荷时，腹板等效宽度取为筋条净间距时，计算得到的屈曲载荷与线性屈曲载荷较为接近，但由于实际筋条的铺层数较少，不能为腹板的屈曲提供足够的支撑，因此理论计算得到的屈曲载荷高于有限元线性屈曲载荷计算值;而腹板等效宽度取为筋条中心间距时，计算得到的屈曲载荷与非线性屈曲载荷较为接近。

图2 有限元分析模型

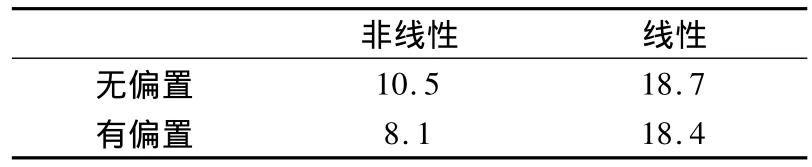
表3 初始屈曲载荷的有限元计算(单位:kN)

线性屈曲理论对于结构的稳定性分析基于小挠度、线弹性的假设，没有考虑受载后的变形对平衡状态的影响，适用于比较刚性的结构。而结构受压的加筋板结构实际上是在变形后的位置上处于平衡状态的，从加载一开始就具有几何非线性的特点。对于受压的薄壁加筋板，非线性屈曲载荷明显低于线性屈曲载荷。在对这一类结构进行稳定性设计的时候，要考虑几何非线性的影响。

2 试验结果分析

为进一步修正和确认屈曲、后屈曲分析方法，在初始屈曲载荷分析的基础上进行了复合材料加筋板的压缩试验。试验在CSS-10试验机上完成，加载为纵向加载，加载速度为0.3mm/s。加载时试验区两侧通过立柱和前后挡板约束，上下通过夹具约束，如图4a所示。试验件正反面各布置12枚应变片，位置及编号如图4b所示。同时，在试件反面采用云纹影像观察离面位移。

图3 有限元计算得到的变形和初始屈曲模态

图4 压缩试验图

对6件试验件的试验结果表明，5件试验件破坏时3根筋条端部均脱粘，且左、右两筋内侧脱粘区域较大;1件试验件中筋和右筋端部脱粘，且右筋内侧脱粘区域较大。试验件平均破坏载荷为12.29kN，平均破坏位移为1.21mm。通过云纹影像观察可见，随着载荷的增加，面板出现不同的变形模态。

测点1正反两面的应变-载荷曲线如图5所示(试验值为选取一件典型试验件的结果，下同)。正反两面的应变曲线有明显的反向分离，说明发生了局部屈曲。

通过与初始屈曲载荷的计算值进行比较，结构的线性屈曲载荷高于试验中的结构破坏载荷，表明按照线性屈曲分析，结构发生破坏前不会发生屈曲;而非线性屈曲载荷低于结构破坏载荷，表明按照非线性屈曲分析，在结构发生破坏前腹板就会发生局部屈曲。

图5 测点1正反两面应变-载荷曲线

由云纹影像观测到的位移结果可见在加载过程中腹板会呈现如图3c所示的变形模式，并且根据图5应变曲线的分离，说明发生了局部屈曲。因此，非线性下的初始屈曲载荷和模态与试验相符合，进一步证明了在对受压的薄壁加筋板进行稳定性设计的时候，必须考虑几何非线性的影响，如果按照线性屈曲载荷设计会偏于危险。另一方面，结构在发生局部屈曲后，仍具有一定的继续承载能力，为分析其极限承载能力，需要进行后屈曲分析。

3 加筋板压缩的后屈曲分析

3.1 初始有限元模型

针对本试验观察到的结构后屈曲特性，使用MSC.Marc进行数值模拟，并使用不同的分析参数与试验结果进行比较。

在图2的有限元模型的基础上建立后屈曲分析模型，为更精确地模拟试验加载情况，顶部由均布载荷加载改为通过刚性面接触加载。材料的失效模型为基于Tsai-Wu准则的渐进失效模型，并添加前五阶屈曲模态作为初始几何扰动进行后屈曲分析。

计算得到的载荷-位移曲线与试验值比较如图6所示。结果表明数值模拟与试验之间存在较大差异，主要包括以下几个方面:计算得到的结构总体刚度远高于试验值;计算得到的结构最大载荷和对应位移也远高于试验值;计算结果中结构具有明显的软化现象，而在试验结果中没有表现。因此初始模型无法正确模拟试验件的力学行为，必须对模型和分析参数进行调整。

3.2 引入胶层单元的后屈曲分析

在面板和筋条粘接区的界面上引入0.1mm厚度的三维实体元模拟胶层进行计算。计算得到载荷-位移曲线如图7所示。计算结果表明，胶层的引入使结构总体刚度进一步增加;由于胶层的失效使得结构的总体破坏位移计算值减小;筋条与面板脱胶以后结构总体仍有一定的承载能力。

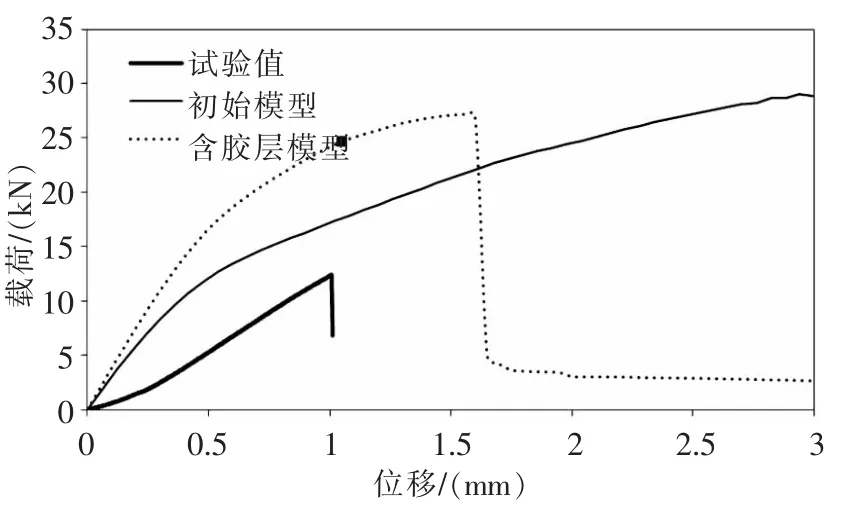
图7 初始模型和含胶层模型的载荷-位移曲线比较(图中的标记点为初始脱胶点)

含胶层模型计算得到的最大载荷和对应位移与试验值相比仍有较大差异，即使是初始脱胶载荷也远高于试验得到的结构破坏载荷。因此单纯在模型中引入胶层不能有效减少和试验值的误差，需要更改铺层的失效参数。

3.3 铺层失效模型的影响

在渐进失效模型中，使用刚度折减系数r表征材料的失效。即在每一个增量步结束时，如果失效系数F大于1，则按公式Δr=-(1-e1-F)计算刚度折减系数。在下一增量步计算时按E=rE0对材料的弹性模量、剪切模量和泊松比等参数进行折减。

而根据试验结果，结构并没有表现出明显的软化现象，因此可以认为复合材料的塑性效应不明显，当结构发生局部屈曲后，可能随时发生分层、纤维断裂和基体开裂等破坏形式，并且一旦发生，会使截面上的某些稳定区域产生应力集中，从而加速结构的破坏。

因此，在复合材料薄壁结构的后屈曲分析中，并不适合用渐进失效模型表征材料失效后的行为，而应采用立即失效模型(即当失效系数F大于1的时候立即将材料的刚度折减到0)。采用渐进失效模型和立即失效模型计算得到的载荷-位移曲线如图8所示。由图中可见，计算得到的结构最大载荷和对应位移与试验值较为接近。在模型中引入胶层时，由于胶层的失效使得结构的总体破坏位移计算值减小，但由于胶层增加了整个结构的刚度，计算得到的总体破坏载荷反而有增大。

三种模型计算得到的失效分布如图9所示。由图中可见渐进失效模型计算得到的失效位置位于筋条端部外侧，与试验情况不符;立即失效模型计算得到的失效位置位于中间筋条端部和两侧筋条端部内侧，并且两侧筋条端部内侧有较大面积失效，与试验情况接近。

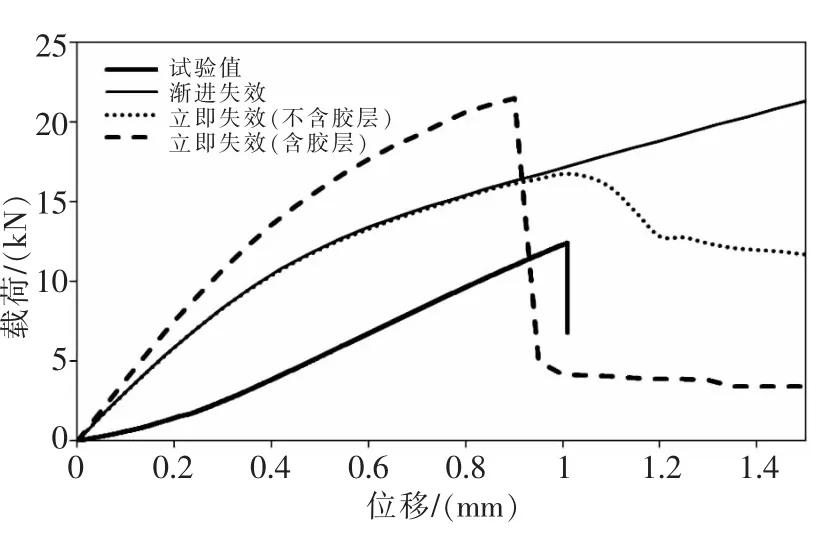
图8 渐进失效模型和立即失效模型的载荷-位移曲线比较

3.4 模拟与试验的应变对比

有限元模拟与试验得到的应变数据曲线如图10所示。可以看出，在结构失稳之前，应变随载荷的变化近似呈线性关系;失稳后，筋条上的应变增大，且壁板正反面的应变开始分离，说明壁板的一部分轴向位移向面外位移转化，并且载荷向筋条转移。在加载过程中，中间面板和筋条端部的连接胶结界面首先发生破坏导致应变的下降，并使得筋条中部的承载进一步增加，最终导致结构的破坏。含胶层单元的模型与不含胶层单元的模型相比，由于结构刚度的增加，计算得到的应变值偏低，应变分离载荷偏高，与试验值相比偏差较大。

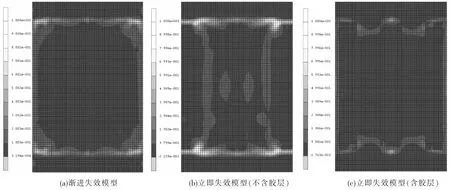
图9 渐进失效模型和立即失效模型的失效分布

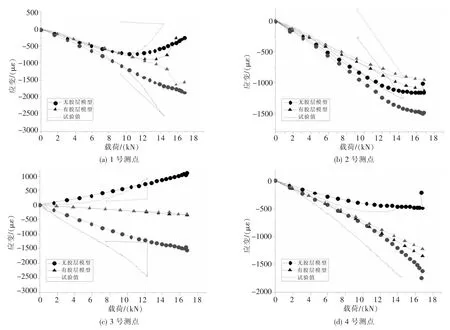
图10 各测点的试验和有限元应变值比较

总体来说，对于复合材料薄壁加筋板结构，由于试件的制造缺陷和边界条件对结构的力学行为具有较大影响，试验值和模拟值仍存在一定偏差。不含胶层单元的模型模拟结果与试验值较为接近，因此在实际设计过程中可以用不含胶层单元的模型预测结构的破坏载荷和失效模式。

4 结论

本文研究的复合材料薄壁加筋板在轴压载荷下，首先面板发生局部失稳，载荷向筋条转移，随后面板和筋条端部的连接胶结界面发生损伤，筋条中部的承载进一步增加，最后，损伤扩展导致结构的破坏。因此，在进行复合材料加筋板设计时要加强筋条端部与面板之间的细节设计，防止面板失稳引起界面的损伤。

加筋板受压时，从加载一开始就具有几何非线性的特点。在计算结构的屈曲载荷时应考虑这一特点，否则会使计算结果偏于危险。使用有限元计算时，应开启几何非线性的选项;使用理论计算时，对腹板等效宽度和边界条件的选择需要注意。

对于薄壁结构，当结构发生局部屈曲后，仍具有一定的承载能力，但复合材料屈曲后可能随时发生破坏，因此在复合材料薄壁结构的后屈曲分析中，使用立即失效模型表征材料的失效行为更符合实际情况。计算模型中引入胶层单元会使结构刚度偏高，在实际设计过程中，可以用不含胶层单元的模型预测结构的破坏载荷和失效模式。

［1］朱菊芬，杨海平，汪 海，等.复合材料加筋板壳结构的后屈曲强度及破坏分析程序系统［J］.计算结构力学及其应用，1996，13(4):489-493.

［2］杨乃宾，章怡宁.复合材料飞机结构设计［M］.北京:航空工业出版社，2002.

［3］Degenhardt R，Wilckens D，Rohwer K，et al.Improved material exploitation of composite airframe structures by accurate simulation of collapse–The COCOMAT project.2nd Int.Conference on Buckling and Postbuckling Behaviour of Composite Laminated Shell Structures，3-5 September 2008［C］，Braunschweig，Germany.

［4］Koiter W T.On the stability of elastic equilibrium(in Dutch with English Summary)［D］，Delft，H.J.Paris，Amsterdam，1945.English Translation issued as NASA TTF-10，p.833，1967.

［5］Chai G B，Chou S M，Ho C L.Stress analysis of postbuklied laminated composite plate［J］.Struct Eng Mech，1999，7(4):377-386

［6］Orifici A C，Thomson R S，Herszberg I，et al.An analysis methodology for failure in postbuckling skin-stiffener interfaces［J］.Compos Struct，2008，86(1-3):186-193.

［7］Oh S H，Kim K S，Kim C G.An efficient postbuckling analysis technique for composite stiffened curved panels［J］.Compos Struct，2006，74:361-369.

［8］刘从玉.复合材料加筋板的屈曲和后屈曲分析及承载能力研究［D］.南京:南京航空航天大学，2010.

［9］孔 斌.复合材料整体加筋板的轴压后屈曲问题研究［D］.南京:南京航空航天大学，2010.

［10］中国航空研究院.复合材料结构稳定性分析指南［M］.北京:航空工业出版社.2002.

［11］付新卫，刘瑞同，戴 瑛.夹具对复合材料加筋板剪切试验屈曲载荷的影响［J］.力学季刊，2011，32(4):563-569.

［12］Singer J，Arbocz J，Weller T.Buckling Experiments:Experimental Methods in Buckling of Thin-Walled Structures［M］.Chichester:John Wiley＆ Sons，1998.

［13］(荷)卡萨波格罗，著，颜万亿，译.飞机复合材料结构设计与分析［M］.上海:上海交通大学出版社.2011.