WC－Co硬质合金微观结构的参数化模型

王 东，赵 军，李安海，王泽明

（山东大学 机械工程学院 高效洁净机械制造教育部重点实验室，济南 250061）

随着计算数学、统计力学和计算机技术的迅猛发展，利用数值计算和计算机仿真，通过各种算法设计实现材料的微观结构参数化，对现阶段材料的性能预报和微观结构优化有着重要的现实意义［1－5］。

为了避免浪费时间和过度使用实验仪器，有限元分析被用于研究 WC－Co硬质合金的性能［6－10］。但是这些研究都有一定的局限性。XU Z.H.等［6］在使用有限元模型研究 WC－Co硬质合金的硬度时，未考虑材料的微观结构，这与实际不符；SADOWSKI T.等［9］在研究WC－Co硬质合金局部力学性能时使用的模型从真实微观结构图中提取出来，这一方面加大了工作量，另一方面没有考虑微观结构的随机性。因而本工作提出了一种基于“随机法”构建的模型来更好地弥补这个不足。

目前国内外已有学者在研究其他材料性能时使用了考虑微观结构的模型［11－14］，但在 WC－Co硬质合金方面的研究较少。PARK S.等［11］构建了随机的二维WC－Co微观结构模型用来预测刀具在加工过程中的失效；CHUZHOY L.等［12］研究球墨铸铁的加工过程时使用了基于蒙特卡洛法生成的二维微观结构模型；司良英等［13］开发了基于Voronoi图的二维多晶体材料微观结构的模型；李俊琛等［14］应用Voronoi晶粒设计构造了三维异质体材料微观结构模型。

本工作首先分析了 WC－Co硬质合金的微观结构，研究其基本参数的分布规律；其次，提出了 WC－Co硬质合金微观结构参数化建模的方法；最后，通过对比模型的设计参数和实际参数以及分析模型基本参数的统计结果，验证了建模方法的可行性和模型的可靠性。

1 WC－Co硬质合金微观结构的参数分析

使用扫描电镜（SEM）观察各种 WC－Co硬质合金的微观结构。图1所示是测得晶粒平均粒径为1μm，Co相体积分数为15%的合金微观结构SEM照片。WC－Co硬质合金的微观结构基本参数包括 WC晶粒的平均粒径、形心位置、取向角和Co相体积分数。

图1 WC－Co硬质合金微观结构SEM照片Fig.1 SEM micrograph of the WC－Co cemented carbides

从图1可以看出，WC晶粒外形近似为多边形，它一般有四到八条边，镶嵌在黏结相Co中。在微观结构的测量系统中定义了 WC晶粒的形心，长径（A）和短径（B），以及取向角（θ）。晶粒取向角测量的是长轴和水平方向之间的夹角，见图2。多边形勾绘出了晶粒的外形，（×）为晶粒形心，A和B分别代表晶粒长径和短径，θ为晶粒取向角，浅色区域代表 WC晶粒，深色区域代表黏结相Co。

图2 WC－Co硬质合金微观结构的测量参数Fig.2 Measurement of microstructure parameters of WC－Co cemented carbides

通过分析WC－Co硬质合金微观结构参数的统计结果可以发现，其晶粒形心坐标是随机分布的，一定程度上趋于均匀分布，WC晶粒取向角是0～180o之间的随机分布，也趋于均匀分布，而长径（A）和短径（B）是分别服从均值和标准差为（μA，σA）与（μB，σB）的正态分布。表1列出了多种常见WC－Co材料的基本参数［15］。

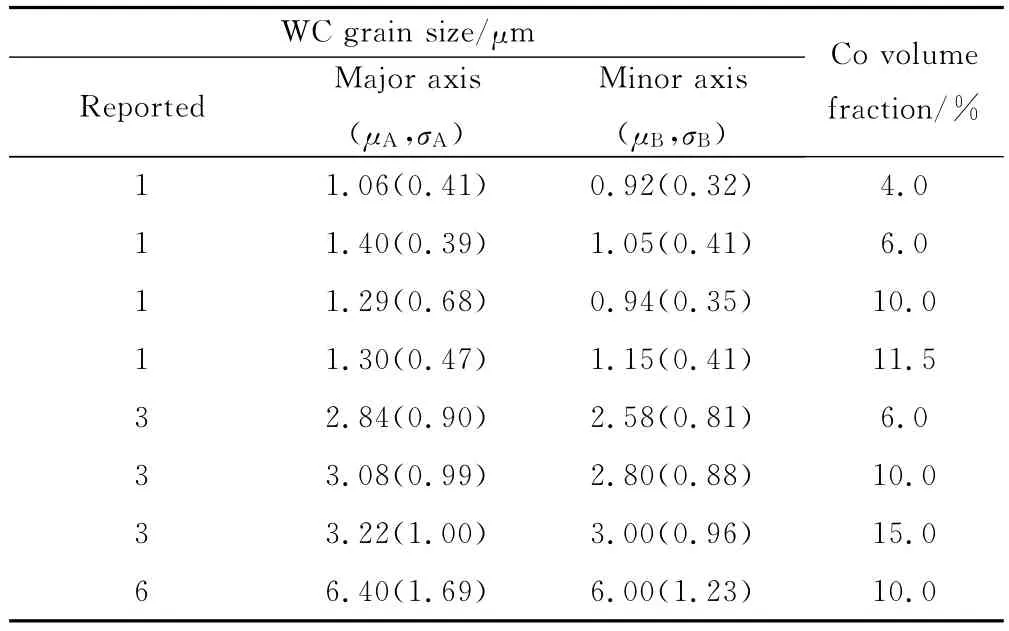
表1 WC－Co硬质合金的常见参数Table 1 Common parameters of WC－Co cemented carbides

2 WC－Co硬质合金微观结构建模

建模的第一步是构建WC晶粒。首先以随机生成的长径（A）和短径（B）为边长创建长方形，A和B分别服从均值和标准差为（μA，σA）与（μB，σB）的正态分布。然后使长方形的四个顶点在以各自位置为圆心，以0.1～0.4倍A的长度为半径的圆上任意改变。最后将生成的四边形绕形心在0～180°之间随机旋转θ角度。至此，单个WC晶粒就构建完成。具体步骤见图3。

图3 WC晶粒模拟步骤Fig.3 Schematic illustration of simulating for WC grains

创建好单个WC晶粒后，在选定的体积代表单元为20μm×20μm的区域里随机投放多边形，这个选定的空区域代表黏结相Co。随着多边形的投放，Co黏结相面积逐渐减小，WC硬质相面积不断增加。在投放过程中不可避免地会产生多边形之间的重叠，采用算法去除重叠部分，从而生成新的多边形，这些新生的多边形就用来代表材料中实际的WC晶粒。去除重叠部分的过程见图4。

图4 重叠部分处理步骤Fig.4 Schematic illustration of processing for overlapped areas

在投放多边形的同时，不断处理重叠部分，然后计算已投放多边形的总面积，剩余空白区域的面积即为黏结相Co的面积，当黏结相Co面积与所选区域面积的比值达到目标值时停止投放，输出模型。这里的目标值为WC－Co硬质合金的Co相体积分数的设计值。程序流程图见图5。

3 建模结果分析

通过上述的建模过程，可以控制WC晶粒的平均粒径分布、长径和短径尺寸分布、形心分布、取向角分布和Co相体积分数等微观结构特征参数。改变输入参数可以得到不同的微观结构模型，这样就可以方便地研究微观结构与宏观性能的关系以及进行性能预报等。使用Matlab，C＋＋和Python语言的汇合编程实现了微观结构的可视化，也得到了可直接导入有限元分析的模型。

图5 建模流程图Fig.5 Flowsheet of modeling

分别以晶粒平均粒径3μm和1.4μm，Co相体积分数15%为设计参数，经过上述的步骤，构建的微观结构模型见图6。

图6 典型微观结构模型 （a）WC平均粒径3μm，Co相体积分数15%；（b）WC平均粒径1.4μm，Co相体积分数15%Fig.6 Typical model examples of microstructure （a）WC average grain diameter 3μm，Co volume fraction 15%；（b）WC average grain diameter 1.4μm，Co volume fraction 15%

为了验证建模方法的可行性与模型的可靠性，对设计出来的模型参数进行统计，并计算其与设计值之间的误差，误差及统计结果分别见表2和图7。

分析表2的数据，可以发现模型的设计参数与实际参数间的误差在可以接受的范围内。尤其晶粒平均粒径的设计值为3μm和6μm时所设计模型比较准确。WC晶粒平均粒径设计值为1μm时，结果不是很理想，这是因为在建模过程中，晶粒尺寸越小，代表体积单元中晶粒就越多，晶粒间发生重叠的几率就越高，从而使得晶粒尺寸比较分散，因此需要进一步完善建模的算法。但总体来讲，本工作所提出的建模方法是可行的。

表2 模型设计参数与实际参数之间的误差Table 2 Error between designed parameters and measured parameters of the model

图7 微观结构模型参数统计结果 （a）形心X 坐标；（b）形心Y 坐标；（c）WC晶粒取向角；（d）长轴；（e）短轴；（f）WC晶粒平均粒径Fig.7 Statistic observation results of microstructure parameters of model （a）Xcoordinate of centroids；（b）Ycoordinate of centroids；（c）orientation of the WC grains；（d）major axis；（e）minor axis；（f）WC average grain diameter

观察图7（a），（b）所示的晶粒形心X和Y坐标的统计结果，可以得出晶粒形心坐标的分布近似为均匀分布，图7（c）所示的晶粒取向角分布的统计结果，也近似为均匀分布，图7（d），（e）所示的晶粒长径和短径尺寸分布的统计结果，可以发现其近似为正态分布，图7（f）所示的晶粒平均粒径分布的统计结果，也近似为正态分布。将这些参数分布与实际材料微观结构参数分布的统计结果进行对比，发现其统计结果符合实际材料微观结构参数的分布规律，从而证明了模型的可靠性。

4 结论

（1）提出构建 WC－Co硬质合金二维微观结构模型的方法，并通过对比模型设计参数与实际参数之间的误差以及分析模型基本参数的统计结果，证明了建模方法的可行性和模型的可靠性。

（2）建立了控制 WC晶粒的平均粒径分布、长径和短径尺寸分布、形心分布、取向角分布和Co相体积分数等微观结构的参数化模型，初步实现了硬质合金微观结构的有限元分析模型的建立。

（3）WC－Co硬质合金微观结构模型的构建，为后续材料性能预报和微观结构优化奠定了基础。

［1］任淮辉，李旭东.二维材料微结构设计与数值模拟软件系统［J］.计算机辅助设计与图形学学报，2009，21（6）：861－868.

［2］赵金龙，邓建新，宋文龙.MoS2软涂层刀具的基体材料优选及涂层制备［J］.材料工程，2007，（12）：30－34.

［3］马宁，张宗华，胡平，等.热成形金属复合材料的微观结构及力学行为研究［J］.材料工程，2011，（5）：88－92.

［4］张海泉，张彦华，赵海燕，等.镍基高温合金电子束焊缝形貌预测模型及其验证［J］.航空材料学报，2004，24（5）：21－25.

［5］KIM C S，MASSA T R，ROHRER G S.Modeling the relationship between microstructural features and the strength of WC－Co composites［J］.International Journal of Refractory Metals ＆ Hard Materials，2006，24（1－2）：89－100.

［6］XU Z H，AGREN J.A modified hardness model for WC－Co cemented carbides［J］.Materials Science and Engineering A，2004，386（1－2）：262－268.

［7］HONLE S，SCHMAUDER S.Micromechanical simulation of crack growth in WC／Co using embedded unit cells［J］.Computational Materials Science，1998，13（1－3）：56－60.

［8］VEPREK R G，PARKS D M.Non－linear finite element constitutive modeling of mechanical properties of hard and superhard materials studied by indentation［J］.Materials Science and Engineering A，2006，422（1－2）：205－217.

［9］SADOWSKI T，NOWICKI T.Numerical investigation of local mechanical properties of WC－Co composite［J］.Computational Materials Science，2008，43（1）：235－241.

［10］RONALD W A.The hardness and strength properties of WC－Co composites［J］.Materials，2011，4（7）：1287－1308.

［11］PARK S，KAPOOR S G，DEVOR R E.Microstructure－level model for the prediction of tool failure in WC－Co cutting tool materials［J］.Journal of Manufacturing Science and Engineering，2006，128（3）：739－748.

［12］CHUZHOY L，DEVOR R E，KAPOOR S G.Microstructurelevel modeling of ductile iron machining［J］.Journal of Manufacturing Science and Engineering，2002，124（2）：162－169.

［13］司良英，邓关宇，吕程.基于Voronoi图的晶体塑性有限元多晶几何建模［J］.材料与冶金学报，2009，8（3）：193－197.

［14］李俊琛，李旭东，盛捷.异质体材料三维微观组织结构的可视化仿真［J］.吉林大学学报：工学版，2010，40（1）：92－97.

［15］SUNGHYUK P.Development of a microstructure－level finite element model for the prediction of tool failure by chipping in WCCo systems［D］.Illinois：The University of Illinois at Urbana－Champaign，2007.