擒纵式逃生器的动力学分析与运动仿真

黄佳军，项辉宇，冷崇杰，韩宝安，周小庄

（北京工商大学 材料与机械工程学院，北京 100048）

0 引言

随着建筑高度的增加和日趋紧密，其安全隐患也越来越多。当人们在遭遇到火灾或者其他危害时，由于时间、空间等诸多因素的限制，被困人员自救逃生就变成了一个亟待解决的问题[1,2]。为了提高逃生时的成活率，人们发明了各种各样的逃生器，目前国内外的高楼逃生器主要有以下几种形式：①包角加手控式[3]。此类专利设法增加钢丝绳与轮之间的包角，使得钢丝绳与钢丝轮之间的摩擦力增加。另外，再利用手控装置，进一步调节下降速度的快慢；②间歇冲击式[4]。间歇冲击式是通过间歇撞击能来消耗能量，它要求主动件与从动件之间压力角和摩擦力尽量大，但不能自锁；③液体流动阻尼式[5]。液体流动阻尼式是利用液体流动阻尼把人体势能转化成液体热能，以达到降低速度的目的。

通过对上述几种逃生器的分析，笔者认为逃生器应侧重结构紧凑，工艺简单，安全可靠、使用方便、平稳快速、成本低廉等特点。基于此，提出了利用擒纵式的高楼逃生器。此设计由于小巧便捷，成本低，特别适宜家庭备用于紧急脱险。

1 工作原理

擒纵式逃生器的总体结构如图1所示。它由7个主要的零件组成：3 大转轮、7 棘轮、4 第一级齿轮、5 第二级齿轮、6 第三级齿轮、37 擒纵叉、架子，其中棘轮和擒纵叉决定了该系统的频率。

逃生时，将大转轮上的绳子末端与人固定，随着人的下降，绳子带动转轮旋转。由于与同一轴连接，第一级齿轮与转轮以相同的转速运动。通过齿轮啮合，运动被传递至第二级齿轮、第三级齿轮及棘轮。棘轮特殊的几何形状使它与擒纵叉在每个周期内发生数次碰撞，它们的碰撞消耗了通过齿轮系传递来的能量，实现了加速和减速交替的间歇性运动，同时达到了控制轮系的转速的目的。

纵叉往复振动的周期与擒纵叉转动惯量的平方根成正比，与棘轮给擒纵叉的转矩大小的平方根成反比，因擒纵叉的转动惯量为常数，故只要棘轮给擒纵叉的力矩大小基本稳定时，就能使棘轮做平均转速基本恒定的间歇运动。

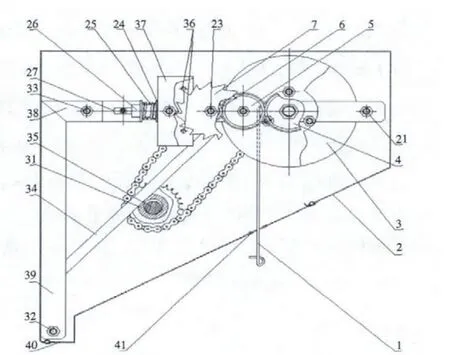
图1 擒纵式逃生器简图Fig.1 Escapement escape device diagram

2 运动学分析

采用分段方法研究平衡摆振动周期的计算方法将平衡摆的振动周期T 分为四个阶段，即T=t1+t2+t3+t4，式中t1和t2 分别为棘轮给进销和出销传冲的时间；t3 和t4 分别是出销和进销作用于棘轮上使棘轮后退的时间。还认为t3和t4 可忽略，因而有：T=t1+t2，建立平衡摆运动方程：

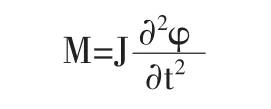
式中：M—传递给平衡摆的力矩；J—平稳摆的转动惯量；φ—平衡摆转角。将M 视为常数，对上式积分：

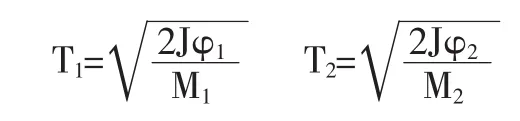
式中：φ1，φ2—沿进销和出销传递冲量时平衡摆的转角；M1、M2—在进销和出销上平衡摆所受的力矩。平衡摆总的振动周期为：

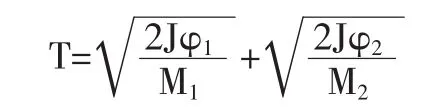
对擒纵机构实际计算后指出，在进销和出销上的传冲时间t1和t2 是不相等的。如果认为进销和出销上的传冲特性相同，则有：，上式若以擒纵轮力矩Mx表示则有[6]：

式中rp，rw分别为销钉半径和擒纵轮半径。又得擒纵轮上的等效力矩公式[7]：

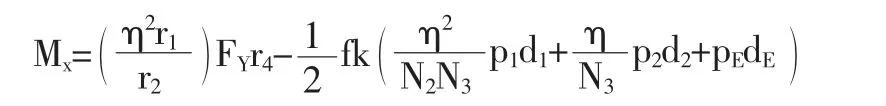
式中：η—传动效率；N2、N3—第一过渡轮与第二过渡轮轴、第二过渡轮与擒纵轮轴间的传动比；FY—人的重力；f—摩擦系数；r1—大转轮半径；r2—第一级齿轮半径；r4—第三级齿轮半径；k—过载系数；p1，p2，pE—第一过渡轮部件、第二过渡轮部件、擒纵轮部件动量；d1，d2，dE—第一过渡轮轴、第二过渡轮轴、擒纵轮轴直径。做初步计算可以假设该系统没有摩擦，则将）看做为0；则：

又因为擒纵叉每转动一个周期，棘轮转动一个齿数，得：

式中：w—棘轮转动的角速度；n—棘轮的齿数；T—擒纵叉的周期。 将式（1）带入式（3）得：

再将式（2）带入式（4）中得：

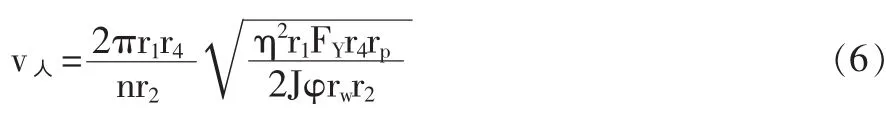
由此可得，当擒纵式逃生器系统整体参数不变的情况下，人下降的速度只与人的重量有关，并且与其开平方成正比。

3 三维虚拟实体建模

（1）基于特征的参数化虚拟实体建模。建立模型是仿真工作的第一步，也是十分重要的一步，对仿真结果的准确性有很大的影响。采用建立虚拟实体模型的方法对擒纵式逃生器进行研究。

虚拟实体模型是指在计算机上利用建模软件Siemens NX8.0，把现实世界中实体的形体结构参数特性完全再现出来，成为一种虚拟的实体模型。

（2）建立零件模型。这一步建模过程类似于车间中通过各种机械加工方法加工零件的过程。建立零件模型就是把要塑造的几何形状添加到模型中，或者使用工具将不需要的部分按一定几何形状切除掉。在Siemens nx8.0中，这些几何形状就是要创建的模型特征。

（3）建立部件模型。这一步建模工作相当于车间中的装配过程。部件是由下级零部件装配而成的，既可以由单独的零件组合而成，也可以由子部件组成。Siemens nx8.0 利用装配约束关系，将这些单独的零件和子部件组合成具有一定装配层次的部件。

擒纵式逃生器的虚拟模型如图2所示，根据零件模型装配得到部件模型，再总装在一起，得到擒纵式逃生器的虚拟总模型。

图2 擒纵式逃生器虚拟模型Fig.2 Escapement escape device virtual model

4 运动仿真

（1）仿真模型。擒纵式逃生器虚拟模型，如图2所示。在第一轴上加绕转轴的等效力FY。在第一轴上加了个齿轮齿条机构，由于力矩带动齿轮齿条的齿轮旋转，从而带动齿条的平行移动，齿条的速度等与第一轴的角速度乘以齿轮的半径，从而可以由齿条的速度，推断出人下落时的速度v人。 关系式如下[8]：

（2）仿真结果。对该擒纵式逃生器虚拟模型进行运动仿真， 分别取FY的值为20、40、50、60、80、100kg的时候，根据Siemens nx8.0 自带的测量功能得出的齿条速度图， 图3、4所示FY为40、100kg时的速度图。

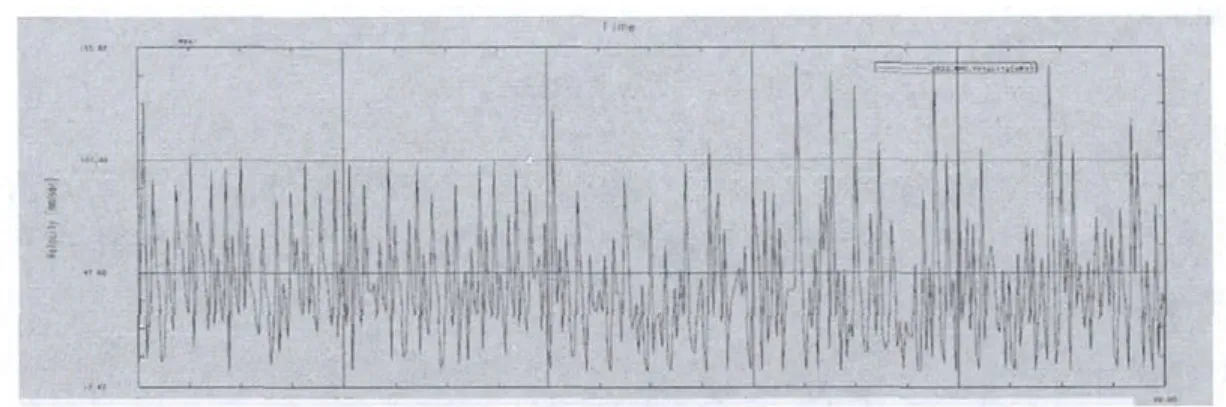
图3 FY=40kg时齿条速度图Fig.3 FY=40kg,rack speed figure

图4 FY=100kg时齿条速度图Fig.4 FY=100kg,rack speed figure

将所得齿条速度的平均值代入式（7）中，得不同质量的人在利用该逃生器的时候下降的速度粗值。

当 FY=20kg时，v 人≈0.1390； 当 FY=40kg时，v人≈0.1980；当 FY=50kg时，v 人≈0.2205；当 FY=60kg时，v人≈0.2430；当 FY=80kg时，v 人≈0.2790；当 FY=100kg时，v人≈0.3150。

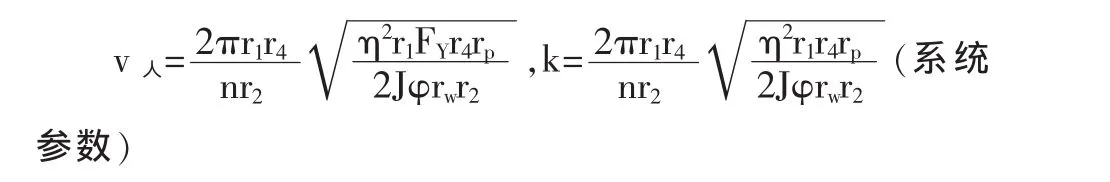
由FY=20kg 得，，推出k≈0.0098

由FY=40kg 得，，推出k≈0.0099

由FY=50kg 得，，推出k≈0.0098

由FY=60kg 得，，推出k≈0.0099

由FY=80kg 得，，推出k≈0.0099

由FY=100kg 得，，推出k≈0.0099

得出K 值基本相同，所以可以确定下降的速度只与人的重量的开平方成正比这一关系。并且正比系数K 约为0.0099， 即

5 结论

以擒纵式逃生器为研究对象，采用振动周期的简单算法，建立了动力学模型，得出结论人下降的速度与人的重量的开平方成正比。又以Siemens nx8.0 模拟了该逃生器的模型，并对其进行了运动仿真，揭示了该逃生器的动力学特性。从数据得出人下降的速度与人的重量的开平方成正比。综合数学模型与运动仿真的结论，得出该逃生器的虚拟模型在描述和预测动力学问题上具有较高的精度。

[1]王春彦，岳大鑫.基于弹簧的新型高楼逃生器[J].机械，2007，6.

[2]尹凌鹏.摩擦片式高楼缓降逃生器[J].机械，2012，6.

[3]白阳光.高楼逃生安全控制器 [P].中国专利：89103555.9，1990/2/19.

[4]曾景霖.高楼救生高楼逃生器 [P].中国专利：93239887.1，1994/08/24.

[5]叶强.液体流动阻尼式高楼逃生器的创新与设计[J].消防设备研究，2005，2.

[6]魏亚果，等（译）.定时器及其元件[M].国防工业出版社，1985.

[7]尚雅玲,马宝华.销钉式无返回力矩钟表机构振动周期的研究[J].探测与控制学报，1999，4.

[8]茅健,傅裕.机械手表擒纵机构动力学分析与仿真[J].机械科学与技术，2011，9.