关于矩阵方程求解的讨论

谢世伟， 张明虎

（石家庄职业技术学院a.管理系；b.信息工程系，河北 石家庄 050081）

现行的高等院校教材《高等代数学》［1］《高等代数》［2］《线 性 代 数 》［3］《工 程 数 学 》［4］中，均 有 形 如AX＝B，XA＝B，AXC＝B（A为可逆矩阵）的矩阵方程，但给出解题方法的并不多，特别是对XA＝B和AXC＝B两种方程均未给出解法，这便存在一个在教学中如何为学生解答的问题.我们从适应高职高专数学教学要求的角度出发，来探讨这些形式的矩阵方程的解法，特别是只用初等变换（简称行变换）的求解方法，以便于学生理解和掌握.

1 矩阵方程AX＝B的解X＝A－1 B的求法

方法1：先求出矩阵A的逆矩阵A－1，由即可求得A－1（E 为单位矩阵），然后计算矩阵乘法A－1B，得出结果X＝A－1B.

2 矩阵方程XA＝B的解X＝BA－1的求法

方法1：先求出A－1，然后计算BA－1，得出结果X＝BA－1.

例1 解矩阵方程

解以上矩阵方程为XA＝B的形式，用方法2解答，解题过程如下：

在解题过程中的具体列变换过程如下：（1）做C1－2C2，然后做C3＋C2；（2）做C1＊1／3，然后做C2－C3；（3）做C2＋C1；（4）做C1与C2位置互换，再做C2与C3位置互换.其中，C1，C2，C3分别代表矩阵的第一列、第二列和第三列.

方法3（行变换法）：这种方法的基本原理是，X＝BA－1，则XT＝［A－1］TBT＝［AT］－1BT，据此可先求出XT，再写出X＝［XT］T＝BA－1，即由［AT｜BT］得到XT＝［A－1］TBT，进而得到结果X＝BA－1.

用方法3解例1矩阵方程的过程如下：

3 方程AXC＝B的解X＝A－1 BC－1的求解方法

方法1：先分别求出A－1，C－1，然后得到 X＝A－1BC－1.

例2 解矩阵方程：

解用方法3的求解过程如下：

视方程为AXC＝B，

在解题过程中，每一步具体行变换为：（1）做r2－2r1，再做r3－3r1；（2）做r2－r3；（3）做r1－2r2，再做r3＋4r2；（4）做r1－r3.其中，r1，r2，r3分别代表矩阵的第一行、第二行和第三行.

4 分析与说明

（1）求解矩阵方程AX＝B，可看作是同时对线性方程组AX＝b1，AX＝b2，…，AX＝bn求解，B＝［b1，b2，…，bn］，bi为列矩阵（i＝1，2，…，n，下略），A为可逆矩阵.反之，一个线性方程组AX＝bi可以看作矩阵方程AX＝B中B＝bi的特例.

（2）由（1）决定了用初等行变换求解AX＝bi与AX＝B在原理上的同一和解法上的类似.

原理：①A－1［A＋E］＝A－1A＋A－1E＝E＋A－1，

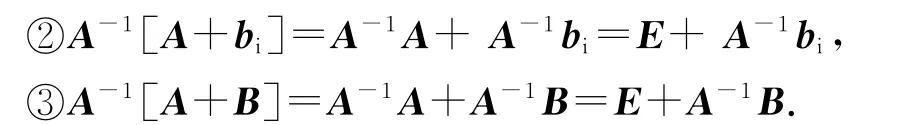
据原理①，先求A－1，然后求X＝A－1bi或X＝A－1B；

（3）我们使用的教材大都略去了原理②及做法，因为AX＝bi可以看作B＝bi的特例.但从认识规律（从个别到一般）以及AX＝bi与AX＝B的关系上说，原理②及作法应保留且先给出.另外，¯A＝［A｜bi］的使用是讨论非齐次线性方程组AX＝b的解的预演，是AX＝b只有唯一解的特殊情形.

（4）矩阵方程AX＝B可以看作XTAT＝BT，亦即XA＝B形态的方程.反之，XA＝B也可以看作ATXT＝BT，亦即AX＝B形态的方程.这是用行变换求解形如XA＝B方程的根本原理.由此可知，上述的用行变换求解XA＝B的方法的实质是用行变换求出ATXT＝BT的解XT，进而得到原题的解X.

以上所谈解题方法及例题的解答过程（要求）是否合理，是否符合高职高专教学实际，是否存在观点和科学性错误，还需要相关专家的指导和在教学实践中加以验证.

［1］姚慕生.高等代数学 ［M］.上海：复旦大学出版社，2003：73.

［2］北京大学数学系几何与代数教研室代数小组.高等代数 ［M］.北京：高等教育出版社，2005：202.

［3］石有印，胡长春.线性代数 ［M］.北京：冶金工业出版社，2010：52.

［4］石宁，高惠，王敏.工程数学 ［M］.北京：中国水利水电出版社，2010：31－32.