基于Copula函数的风速相关性建模及概率最优潮流分析
2013-09-13徐玉琴张林浩
徐玉琴,张林浩
(华北电力大学 电气与电子工程学院,河北 保定 071003)
0 引言
针对日趋严重的环境问题与能源危机,风电产业的开发利用受到了国家的高度重视,成为发展速度最快的新能源发电方式[1]。风能具有随机性、间歇性的特点,同时由于风力资源的地域分布特征,风电场往往以集群方式接入电网,这些特性对电力系统的稳定运行与经济调度产生了一定影响。
在现有的最优潮流分析方法中,一般假定各风电场之间的风速是相互独立的[2],事实上,风电场都选址在风能资源充裕的地区,地理位置比较接近,其风速具有较强的相关性,从而各风电的出力也存在较强的相关性[3]。因此,在分析最优潮流的过程中,应该考虑到风速相关性因素。由于多采用威布尔(Weibull)概率分布函数来描述风速的分布特性,研究风速相关性问题的关键在于正确处理非正态相关变量之间的相关性。文献[4]采用了三阶多项式正态变换技术来产生具有指定边际概率分布及相关性的多变量随机数,并应用于概率最优潮流分析。文献[5]采用Nataf逆变换技术建立不同风电场之间具有相关性的风速分布样本空间,进而得到具有相关性的风电场出力。在最近的研究中,Copula函数逐渐应用于随机变量相关性问题的处理。文献[6]基于多个实测负荷水平的相关性,采用Copula函数建立了具有相关性的负荷需求样本。文献[7]介绍了基于Copula函数构建电力系统随机变量之间的联合概率计算方法,并利用正态Copula函数描述离岸风电场与近岸风电场出力之间的相关性。与其他方法相比,利用Copula函数描述随机变量相关性的优点主要有两点:第一点是边缘分布的选择不受限制,即便是服从不同分布的随机变量,其相关性也可以用Copula函数刻画;第二点是Copula函数可以描述随机变量之间的非线性相关性,并且对变量进行非线性单调增变换时,由Copula函数导出的相关性测度不会发生改变。
本文利用Copula函数构建多风电场的风速相关性模型,针对风电的不确定性,采用基于机会约束规划(Chance Constrained Programming,CCP)的电力系统概率最优潮流(Probabilistically Optimal Power Flow,P-OPF)模型,利用一种基于随机模拟技术的粒子群优化(Particle Swarm Optimization,PSO)算法对上述模型进行求解。最后,以实际风电场的历史风速数据和IEEE-30节点测试系统为算例,验证本文所提方法的合理性与有效性。
1 基于Copula函数的风电场相关风速建模
1.1 Copula函数的概念
Copula是一个定义在N维[0,1]空间内的多元同一分布函数[8],其实际意义是一类将联合分布函数与它们各自的边缘分布函数连接在一起的函数,因此也称为连接函数,其理论基础是Sklar定理。
Sklar定理:令 F(·,…,·)为具有边缘分布F1(·),F2(·),…,FN(·) 的联合分布函数,那么存在一个Copula函数C(·,…,·),满足:

若 F1(·),F2(·),…,FN(·) 连续,则 C(·,…,·)唯一确定;反之,若 F1(·),F2(·),…,FN(·) 为一元分布,C(·,…,·)为相应的 Copula函数,那么由式(1)定义的函数F(·,…,·)是具有边缘分布F1(·),F2(·),…,FN(·) 的联合分布函数。
可以看出,Copula函数建立了边缘分布到联合分布的映射关系,利用Copula函数,可以将边缘分布与变量之间的相关结构分离,从而减小含非正态相关变量模型分析的难度。
1.2 Copula函数的分类
常用的Copula函数分为正态Copula,t-Copula和阿基米德 Copula,其中阿基米德 Copula包括Gumbel-Copula,Clayton-Copula 以及 Frank-Copula,下面主要介绍阿基米德Copula函数的相关概念和特性。
阿基米德Copula(Archimedean Copula)分布函数的表达式为

式中:φ(·)称为阿基米德Copula函数的生成元(generator),由表达式可知,阿基米德Copula函数由其生成元唯一确定,三种常见阿基米德Copula函数的生成元如表1所示,其中t∈[0,1],表示Copula函数所描述的边缘分布函数;θ代表生成元相关参数,与随机变量的相关性程度有关。对应于建立风电场风速联合概率分布而言,t即为各风电场风速的边缘分布;θ表征各风电场风速的相关性程度。

表1 阿基米德函数的生成元Tab.1 Archimedean Copulas generators
其中,Gumbel-Copula的密度函数图像呈“J”字形,上尾高,下尾低,对变量在分布的上尾部的变化比较敏感;Clayton-Copula的密度函数图像呈“L”字形,下尾高,上尾低,能够捕捉到下尾相关的变化;Frank-Copula具有对称性,尾部相关系数为0,适用于描述具有对称相关结构的随机变量。
1.3 Copula函数的选取
选取适当的Copula来描述多风电场风速的相关结构,是得到相关性风速样本空间的首要步骤。有多种Copula函数的选取方法,本文采用基于经验Copula(Empirical Copula,EMC)和理论Copula(Theoretical Copula,THC)的最短欧氏距离法[8]来对Copula函数进行选取。
设N个风电场的风速向量为V=(V1,V2,…,VN),其中 Vi(i=1,2,…,N) 的概率密度函数fi(vi)以及累积分布函数Fi(vi)已知,风速向量的EMC可由下式求得:
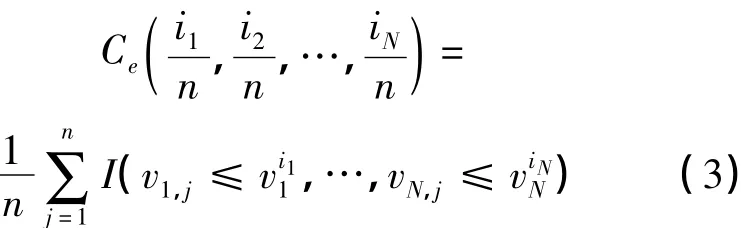
式中:I(·)为示性函数,括号中的条件满足时,I=1,反之为0;{(v1,j,v2,j,…,vN,j),j=1,2,…,n}为容量为n的风速观测样本;为顺序统计量,1≤ i1,…,iN≤ n 。
得到EMC后,可由下式计算EMC与THC之间的欧式距离:

得到计算结果后,选取欧式距离最小的Copula函数作为描述风电场间风速相关性的连接函数。
1.4 基于Copula函数的相关性风速
利用选取的Copula函数并结合式 (1),可以得到各风电场风速的联合概率分布函数:

例如:选取Gumbel-Copula作为描述风速相关性的最佳函数,将边缘分布函数Fi(vi)代入Gumbel-Copula的生成元,可以得到具体的风速联合概率分布函数:

式中:参数θ可用最大似然法进行估计。
利用上述Copula函数相关理论,计算具有相关性的风电场风速样本空间和出力,算法流程如图1所示。
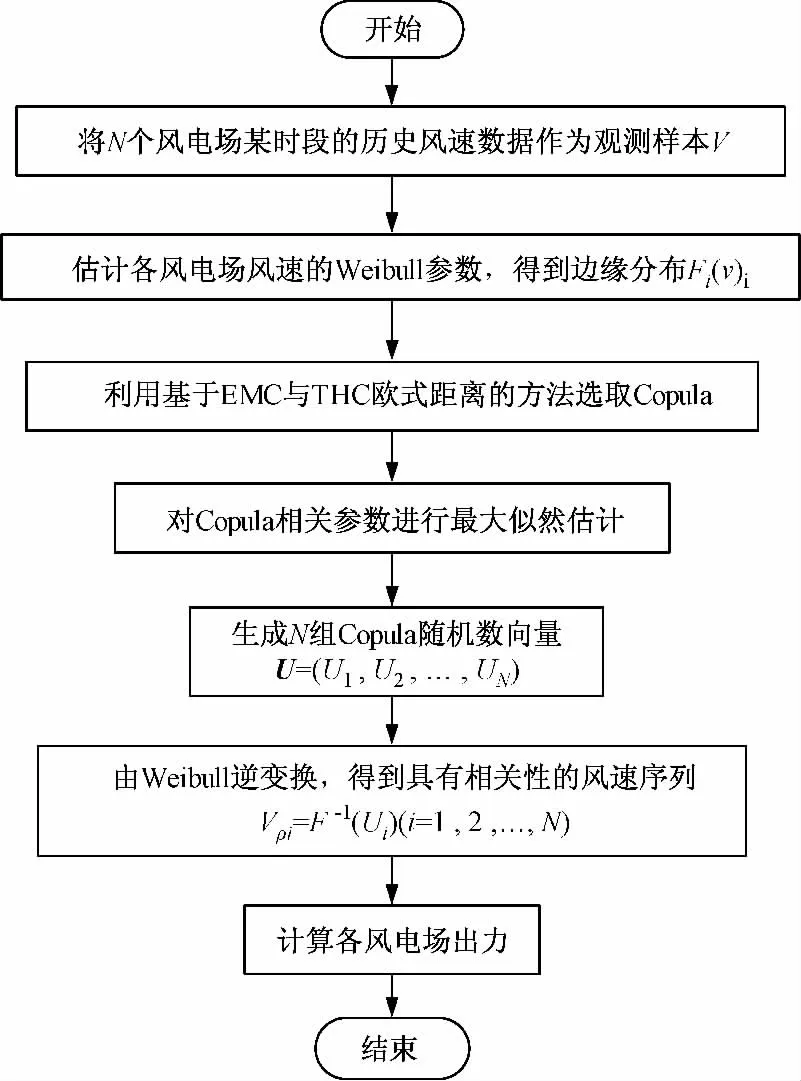
图1 基于Copula函数的风速和出力计算框图Fig.1 Calculation diagram of wind speed and output power based on Copula function
2 基于机会约束规划的最优潮流模型
风电场的出力具有随机性,此时宜引入机会约束规划理论,以解决约束条件中含有随机变量,且必须在观察到随机变量的实现前做出决策的情况。考虑到所做决策在不利情况下可能使约束条件不满足,而采取一种原则:即允许所做决策在一定程度上不满足约束条件,但该决策应使约束条件成立的概率不小于某一置信水平[9]。本文建立了风速相关情况下基于机会约束规划的含风电场电力系统概率最优潮流模型。
2.1 目标函数
模型以常规机组的发电成本最低作为优化目标,表达式如下:
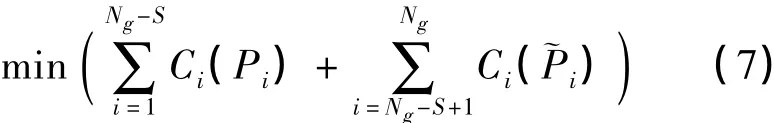
式中:Ng为常规机组数;S为其中平衡机组数;C(P)=αcP2+βcP+γc,为常规机组的发电成本函数,αc,βc,γc为相应系数;Pi为非平衡机组有功出力;为平衡机组有功出力。
由于风电出力的不确定性,平衡机组为了配合风电场的运行,其发电功率也是随机量。对于n个随机风速样本,可计算出n个风电场出力,忽略系统损耗,用负荷减去风电场的发电功率和非平衡机组的发电功率,即可得到n个平衡机组出力,从而计算出n个目标函数值,取其平均值作为对目标函数的估计。
2.2 等式约束
等式约束为系统功率平衡约束,表达式如下:
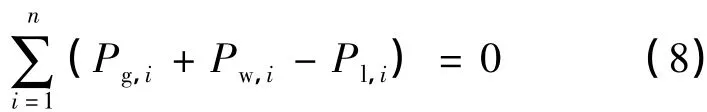
式中:n 为系统总节点数;Pg,i,Pw,i,Pl,i分别为节点i上的常规机组发电功率、风电场发电功率以及负荷需求。
2.3 不等式约束
模型中的控制变量为常规机组的发电功率,其不等式约束为

本文考虑的状态变量有节点电压幅值、常规机组无功出力、线路传输功率以及系统的旋转备用。由于风电出力的不确定性,潮流计算后得到的状态变量也都是随机变量,利用机会约束规划,将不等式约束条件的表达式表述为概率形式,使之在一定的置信水平上成立,具体如下:

式中:Pr{·}为 {·}中事件成立的概率;上标max和min分别表示相应状态变量的上、下限;Ui为节点i的电压幅值;Qg,i为机组i的无功出力;Pli为支路i的传输功率;SPQ为PQ节点集合,Sl为支路集合;Psr为系统的旋转备用,可取系统总负荷的5%;β1~β4分别为相应不等式约束的置信水平。
3 基于随机模拟的粒子群优化算法
3.1 随机模拟技术
随机模拟技术以大量试验作为基础,对计算结果进行概率形式的验证,为处理机会约束规划问题提供了一条有效途径,具体实现的方法如下。
考虑机会约束:

首先,设置N1=0,根据ξ的概率分布Φ(ξ)生成N个随机变量,将控制变量x与生成的随机变量代入式 (11),若满足不等式g(x,ξ)≤0,则N1=N1+1,根据大数定律,当N足够大时,可以用N1/N的数值来估计不等式成立的概率,若N1/N≥β,则机会约束成立,否则不成立。
3.2 基于随机模拟的PSO算法
PSO算法由Eberhart和Kennedy提出,源于对鸟群觅食行为的研究。PSO算法的特点和优势体现在简单易实现,能够记忆个体最优和全局最优信息,并没有太多的参数需要调整,非常适用于工程应用。
本文将随机模拟技术与粒子群算法结合,用以求解含机会约束规划的概率最优潮流问题,具体算法流程如下:
(1)读取系统信息,输入风电场容量、风电机组运行参数及用以建立相关性风速模型的Copula函数的参数;
(2)输入基于随机模拟的粒子群算法参数、约束条件的置信水平以及迭代的终止条件;
(3)随机生成粒子的初始位置,即常规可调机组的有功出力,生成具有相关性的随机风速并计算相应的风电场出力,计算系统潮流,利用随机模拟技术检验粒子的可行性,即不等式约束条件是否达到指定的置信水平,直至生成满足粒子规模n的n个可行初始粒子群位置及速度;
(4)计算各粒子的目标函数值;
(5)获取粒子的个体极值、个体最优位置以及全局极值、全局最优位置;
(6)更新粒子的位置与速度;
(7)计算系统潮流,利用随机模拟技术检验更新后粒子的可行性,若不可行,则重新生成粒子的速度继而更新其位置,直至满足约束条件,如果重复更新的次数超过某一规定的数值,则用原来可行的粒子代替;
(8)重复 (4)至 (7),直至符合终止条件;
(9)输出最优粒子位置及所对应的最优解。
4 算例分析
本文算例分为两部分,第一部分以云南某地区两个风电场2011年1至12月的实际历史风速数据作为样本,选取Copula函数并估计其相关参数,用以生成具有相关性的风速样本;第二部分将两风电场接入IEEE30标准测试系统,应用基于随机模拟技术的粒子群优化算法计算第2节所述的最优潮流问题,并对结果进行分析。
首先对历史风速数据进行处理,利用最大似然估计法估计出两风电场风速的威布尔分布参数如表2所示。
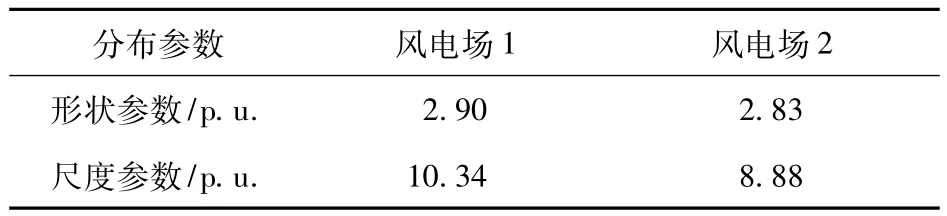
表2 两风电场风速的威布尔分布参数Tab.2 Weibull distribution parameters of the two wind farms wind speed
利用威布尔分布参数可得到两个风电场风速的边缘分布,为便于观察,图2绘制出了两个边缘分布的二元频率直方图。

图2 边缘分布的二元频率直方图Fig.2 Frequency histogram for two marginal distributions
从图2可以看出,频率直方图的上尾高,下尾低,也就是说两个风电场风速的联合密度函数具有在上尾部比较集中的特点,因此可以选取Gumbel-Copula函数描述原始数据的相关结构。
上述分析较为直观,为了得到更客观的评价,利用5种Copula函数分别构建两风电场风速的联合概率分布,通过最大似然估计法估计相关参数,并利用基于EMC与THC的最短欧氏距离法计算5种模型的欧氏距离,结果如表3所示。

表3 两风电场Copula函数参数估计和欧氏距离Tab.3 Parameter estimation and Euclidean distance of Copula function for two wind farms
可以看出,Gumbel-Copula具有最小的欧式距离,能更好地描述两风电场风速的相关性,与利用频率直方图得到的结论是一致的。
下面以IEEE30节点测试系统[10]作为算例,验证上述基于Gumbel-Copula的相关性风速模型、考虑机会约束规划的最优潮流模型以及基于随机模拟技术的粒子群算法的可行性与有效性。该系统有6台常规发电机组和41条支路,假设6号机组不参与优化,其发电功率保持不变,其他机组参与优化,1号机组为平衡机组,配合风电场的运行,可调机组对应于发电成本函数的经济参数及出力上下限如表4所示,系统总负荷为283.4 MW。风电场1,2分别接入节点19和节点20,额定装机容量分别为18 MW和9 MW,风电机组的型号相同,切入风速为3.5 m/s,额定风速为15 m/s,切出风速为25 m/s。

表4 常规发电机组经济、技术参数Tab.4 Economic and technical parameters for conventional units
在置信水平为0.98的条件下,考虑风速具有相关性和风速独立这两种情况,分别进行10次最优潮流计算,计算结果如图3所示。

图3 可调常规机组发电总成本Fig.3 Total fuel cost of adjustable generators
由图3可以看出,当考虑风速相关性时,可调常规机组的发电成本均值要比不考虑风速相关性时略高。分析可知,当风电场间风速相关性较强时,风速同时增大与减小的概率较大,导致风电场出力波动变大,为了配合风电场的运行,常规机组需要更大幅度地调节其出力,从而使发电成本增加;反之,当风速相对独立时,风电场之间的风速呈现出一定的互补性,降低了出力的变化率,较之前一种情况,相对减轻了常规机组的调节负担,发电成本也就随之降低。
在上述模型的基础上设置不同机会约束的置信水平,进行多次最优潮流计算后取平均值可得结果如表5所示。

表5 不同置信水平下的优化结果Tab.5 Optimization results for different confidential levels
由表5可以看出,在相同的置信水平条件下,考虑风速相关性时常规机组发电成本比独立时大,与上述分析一致。观察置信水平对结果的影响,可以看出常规机组发电成本随置信水平的减小而减小,其原因是允许某些违反约束条件的系统状态发生的概率变大,使最优潮流结果不致过于保守;同理,提高置信水平,系统的发电成本随之增大。
5 结论
本文采用Copula函数理论构建了风电场间的相关性风速模型,并生成了相应的风速样本空间;将相关性风速应用于含风电场电力系统概率最优潮流模型,以IEEE30节点测试系统作为算例,通过对计算结果的分析,可得出如下结论:
(1)Copula函数可以有效地描述风速相关性并生成具有指定相关系数的多风电场风速序列,适用于含风电场的电力系统仿真运行分析。
(2)风速相关性的大小会影响到系统发电成本的高低,在制定发电计划或对系统进行安全性评估时,应考虑风速相关性带来的影响。
(3)机会约束规划成立的置信水平越高时,系统发电成本越高,反之越低,因此在实际运行中,可以根据经验或具体情况调整置信水平,在保证安全性的前提下使发电成本最低。
[1]李国清.考虑风电综合利用指标约束的输电规划模型[J].华北电力大学学报,2011,38(2):32-36.
[2]陈金富,陈海焱,段献忠.含大型风电场的电力系统多时段动态优化潮流 [J].中国电机工程学报,2006,26(3):31-35.
[3]肖创英,汪宁渤,陟晶,等.甘肃酒泉风电出力特性分析[J].电力系统自动化,2010,(17):64-67.
[4]杨欢,邹斌.含相关性随机变量的概率最优潮流问题的蒙特卡罗模拟方法 [J].电力系统保护与控制,2012,(19):110-115.
[5]潘雄,周明,孔晓民,等.风速相关性对最优潮流的影响 [J].电力系统自动化,2013,(6):37-41.
[6]Alicja Lojowska,Dorota Kurowicka,George Papaefthymiou,et al.Stochastic modeling of power demand due to EVs using Copula [J].IEEE Trans on Power Systems,2012,27(4):1960-1968.
[7]George Papaefthymiou,Dorota Kurowicka.Using Copulas for modeling stochastic dependence in power system uncertainty analysis [J].IEEE Trans on Power Systems,2009,24(1):40 -49.
[8]Cherubini U,Luciano E,Vecchiato W.Copula methods in finance [M].England:John Wiley Sons,2004:1-30.
[9]刘宝碇,赵瑞清.随机规划与模糊规划 [M].北京:清华大学出版社,1998.74-94.
[10]Zimmerman R D,Murillo-Sanchez C,Deqing G.Matpower:a MATLAB power system simulation package[EB/OL].[2011-11-14].http://www.pserc.cornell.edu/matpower/.
