基于四皇后问题的回溯法求解及算法实现

聂 华

（陕西职业技术学院,陕西 西安,710100）

0 引言

回溯法是一种非常有效，适用范围相当广泛的算法设计思想。许多复杂的问题，规模较大的问题都可以使用回溯法求解，因此回溯法又有“通用解题方法”的美称。本文将利用四皇后问题作为实例，讨论回溯法的求解过程。

1 基本思想

回溯法解决皇后问题的基本思想是：在包含问题的所有解的解空间树中，按照深度优先搜索的策略，从根节点出发深度探索解空间树。当探索到某一节点时，要先判断该结点是否包含问题的解，如果包含，就从该结点出发继续探索下去；如果该结点不包含问题的解，那就说明以该结点为根结点的子树一定不包含问题的最终解，因此要跳过对以该结点为根的子树的系统探索，逐层向其祖先结点回溯。这个过程叫做解空间树的“剪枝”操作。

如果应用回溯法求解问题的所有解，要回溯到解空间树的树根，这样根结点的所有子树被探索到才结束。如果只要求解问题的一个解，那么在探索解空间树时，只要搜索到问题的一个解就可以结束了。

2 四皇后问题的求解过程

许多复杂的问题都可以用回溯法的思想来求解，例如经典的N皇后问题。

N皇后问题的描述为：求解如何在一个N×N的棋盘上无冲突的摆放N个皇后棋子。在国际象棋里，皇后的移动方式为横竖交叉的，因此在任意一个皇后所在位置的水平、竖直，以及45°斜线上都不能出现皇后棋子

N皇后问题的解法很多，可以用回溯法解决N皇后问题。以四皇后问题为例，可以构建出一棵解空间树，通过探索这棵解空间树，可以得到四皇后问题的一种解。这样的解空间树有4棵。如图1所示为皇后问题的一种解空间树。

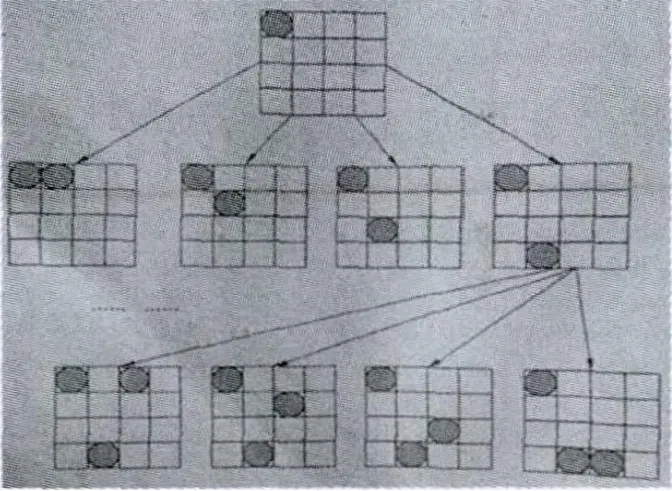
图1 四皇后问题的一种解空间树

由于版面的限制，该解空间树并不完整。该解空间树的根结点为第一个皇后的一种摆法，它还有另外3种摆法，因此一共可以构造出4棵解空间树。通过探索上述这棵解空间树，可以搜索出由根结点这种棋面所产生的所有四皇后的解（如果有解）。

如图1所示，根结点派生出4个子结点。每个结点都示意出前两个皇后可能摆放的位置。每个子结点又可派生出4个子结点，每个结点都示意出前3个皇后可能摆放的位置……整个解空间树为一棵四叉的满树，包含85个结点。

应用回溯法求解四皇后问题，从根结点出发，深度优先搜索整个解空间树。当访问到根结点的第一个孩子时，发现该结点不包含问题的解。也就是说，该结点所示的皇后的摆法不符合四皇后问题的要求，于是停止向下探索，回溯到根结点，以尽快找到问题的答案。实践证明，如图1所示的解空间树中不包含四皇后问题的解。于是需要探索第二棵解空间树，如图2所示。

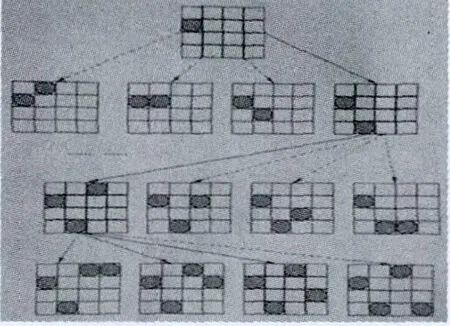
图2 四皇后问题的另一种解空间树

按照上述的探索过程深度优先搜索如图2所示的解空间树，最终可以搜索出四皇后问题的一个解，它的搜索路径在图中用粗体表示，叶结点为四皇后问题的一种解。图中用虚线描绘的结点之间的连线表示在此执行剪枝操作。

3 四皇后问题的算法实现

上一节已经详细介绍了回溯法解决四皇后问题的基本过程。在这里将给出具体的算法描述和程序清单。

其实在解决四皇后问题时，并不一定要真的构建出这样的一棵解空间树，它完全可以通过一个递归回溯来模拟。所以解空间树只是一个逻辑上的抽象。当然也可以用树结构真实地创建出一棵解空间树，不过那样会比较浪费空间资源。

解决四皇后问题的算法描述如下：

在该算法中，用一个二维数组Q[4][4]存放棋盘布局。[i][j]=0表示不放置皇后，Q[i][j]=1表示放置皇后。在这里采用了递归回溯的方法深度优先搜索解空间树，可以将四皇后问题全部解找到并输出。函数Queen()包括两个参数，参数j为放置的皇后所在棋盘的列数，最开始调用Queen()时，j的初始值为0，由它课派生出第一棵解空间树。j的取值范围是0～3，对应着4棵解空间树。当j的值等于4时，表明已得到一个四皇后的解，程序返回。参数(*Q)[4]为指向二维数组每一行的指针。

在该算法中调用了子函数isCorrect(i,j,Q),它的功能是判断棋盘中Q[i][j]的位置是否可以放置一个皇后。它的算法描述如下：

该算法的设计思想是，以Q[i][j]为中心，分别判断二维数组Q的行、列、左上方、右下方、右上方、左下方的状态。如果存在1（有皇后棋子），则表明Q[i][j]的位置不能放置皇后，返回0：否则可以放置皇后，返回1。

4 结束语

综上所述，用回溯法求解四皇后问题时简单易懂，特别适用于求解那些涉及到寻求一组解的问题或者求满足某些约束条件的最优解的问题。本文中很好的诠释了回溯法解四皇后问题的算法设计思想。不仅四皇后问题，例如八皇后问题、子集和数问题、图的着色问题、哈密顿环问题和0/ 1 背包问题等许多复杂的问题，规模较大的问题都可以使用回溯法求解。该方法这对于今后其他问题的研究会有很大帮助。

[1][美]Adam Dro zdek.数据结构与算法( Java 语言版)[M].周翔,王建芬,黄小青,等译.北京:机械工业出版社,2003.139～ 143.

[2]黄建民、罗杰.八皇后问题的非递归算法设计[J]计算机与现代化,2004（5）

[3]卢开澄.组合数学(第2版)[M].北京:清华大学出版社,1991.