一种新型S曲线加减速算法在LED粘片机中的应用

刘 静，武美萍

(江南大学机械工程学院，江苏无锡 214122)

一种新型S曲线加减速算法在LED粘片机中的应用

刘 静，武美萍

(江南大学机械工程学院，江苏无锡 214122)

传统的直线加减速和指数加减速算法在运动过程中的柔性冲击比较大，不能满足如LED粘片机这类设备高速、高效、高精度的要求。针对这种情况，提出了五次多项式拟合的新型S曲线加减速算法，结合LED粘片机的实际应用，给出了位移、速度、加速度及加加速度的函数表达式，并在归一化的基础上，给出了估算最大值的准确表达式，为LED粘片机的加减速控制及电机的合理选型提供了更可靠的参考。

高速高精度;多项式;加减速;LED粘片机

近年来，随着LED市场需求不断扩大，人们对LED装备要求也不断提高，LED粘片机是LED生产过程中的重要设备，它集成了光、电、气等多种科技。LED粘片机主要工作过程为固晶臂将晶圆芯片准确地从蓝膜上取下，并在高速旋转运动后将芯片精确地放到引线框架(或者水平框架)的料碗中［1］。影响LED粘片机性能的主要因素之一是对往复旋转运动的固晶臂的精密控制［2－3］方法。LED晶片的边长从0.15mm到1.00mm不等，而现在市场上的LED粘片机最快固晶速度可达6～8次/s，即固晶臂每秒钟要往复旋转6～8次，高效地实现精确的吸片、粘片。

1 传统加减速曲线分析

要研究固晶臂的加减速特性，首先要了解其运动过程。固晶臂的运动过程如图1所示。

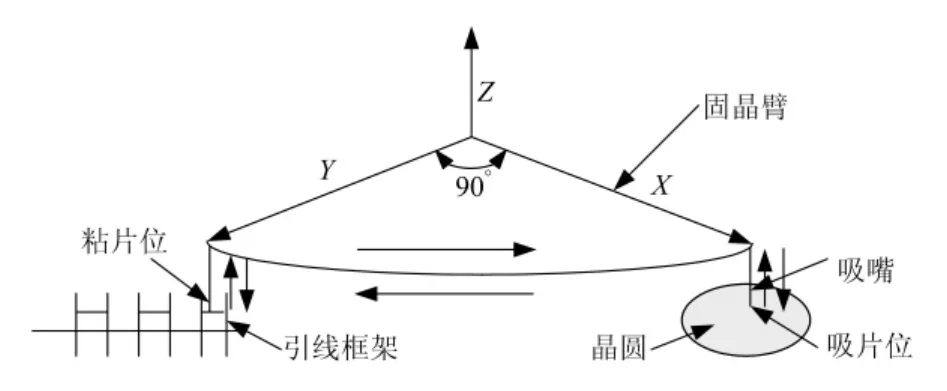
图1 固晶臂运动过程示意图

由图1可见，固晶臂有2个自由度:一个是沿Z向的往复直线运动，实现吸片、粘片过程;另一个是绕Z轴的往复旋转运动，实现晶片的点位转移。在此过程中对固晶臂末端的振动抑制十分必要，除了在结构上采取一定的措施外，还需在运动控制方面采取措施，以设法降低运动过程中的冲击。

系统的加加速度从根本上反映了系统运行的柔性程度，固晶臂往复旋转是粘片过程的主要运动。这种运动速度快、点位精度要求高，为降低运动过程中的冲击，必然要有一种可行的运动控制算法。传统的控制算法是在应用梯形曲线的基础上进行的。传统加减速位移、速度、加速度、加加速度曲线如图2所示。

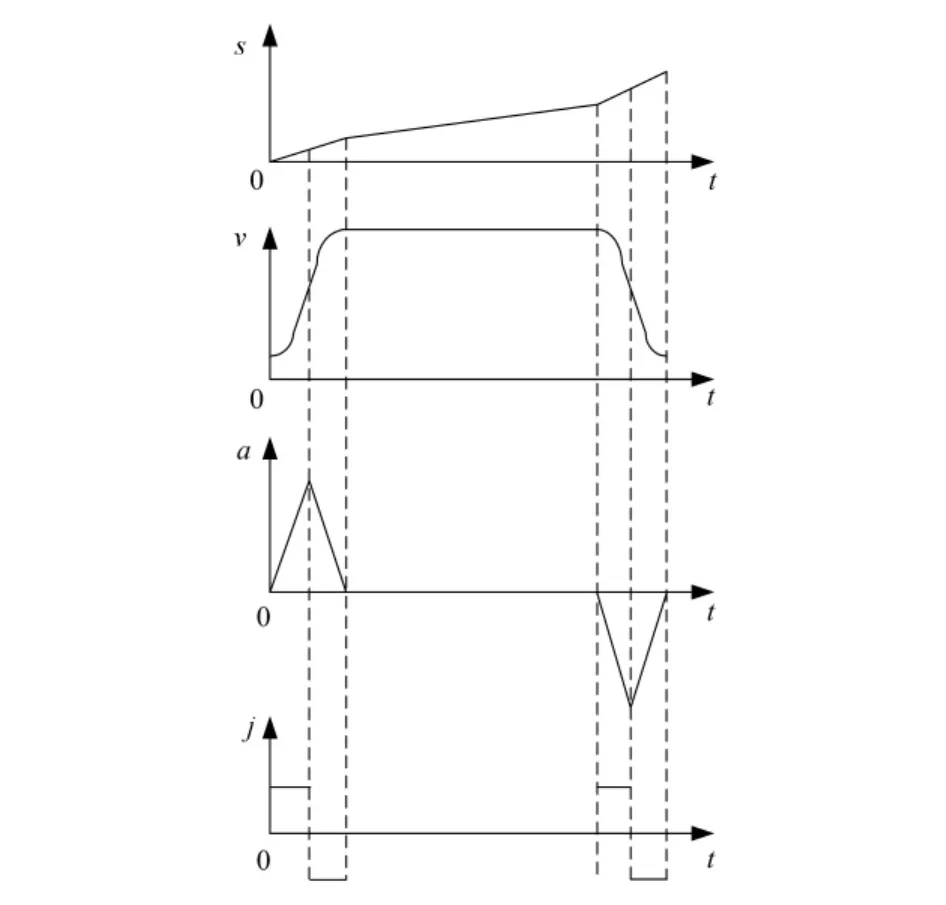
图2 传统加减速位移、速度、加速度、加速度曲线

这种算法的特点是，在运动的初始阶段加加速度从零突变到一个正值，在运动的结束阶段加加速度又突变为零［4］。由此必然会给运动系统带来一定的冲击，给固晶臂在旋转运动的初始及结束阶段带来冲击振动，而不能满足LED粘片机高速、高精度、高效的工作要求。也有人采用分段控制的方法，在运动初始阶段给予系统一个很小的加加速度，实现加加速度的平稳过渡，但是这种算法所涉及的参数很多，系统的复杂程度加大，给控制带来了一定难度［5］。

2 五次多项式加减速控制模型

由高等数学的理论可以知道，任何函数都可以展开成多项式的形式［6］，多项式的阶次越高，越逼近原函数，因此本文提出了基于多项式拟合的五阶多项式加减速控制算法。

为满足LED粘片机的高速、高精度的运动要求，所构造的加减速曲线必须满足速度变化平稳，加速度连续。为保证系统高度柔性，采用五次多项式拟合的方法，这样加速度二阶连续，加加速度一阶连续。构造函数如下:

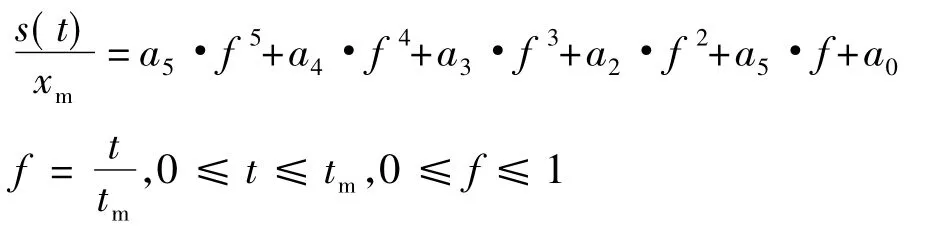
式中:xm为系统规定的位移(包括直线位移及角位移);t为系统运行时间;tm为系统规定的加减速运行时间;a0～a5为参数。

由运动学知识可知:

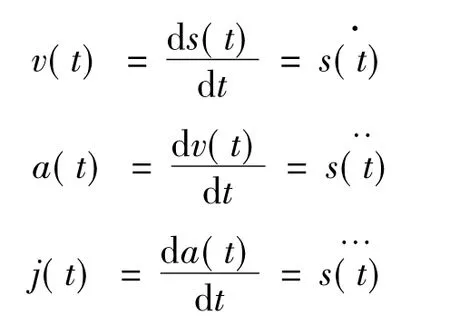
式中:v(t)为速度函数;a(t)为加速度函数;j(t)为加加速度函数。

根据位移与速度、加速度、加加速度的关系得出如下函数关系式:

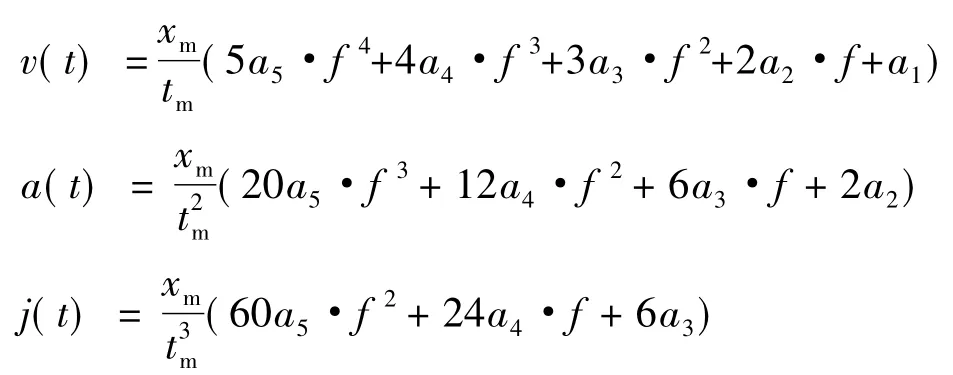
LED粘片机系统在运动初始及结束时有如下边界条件:

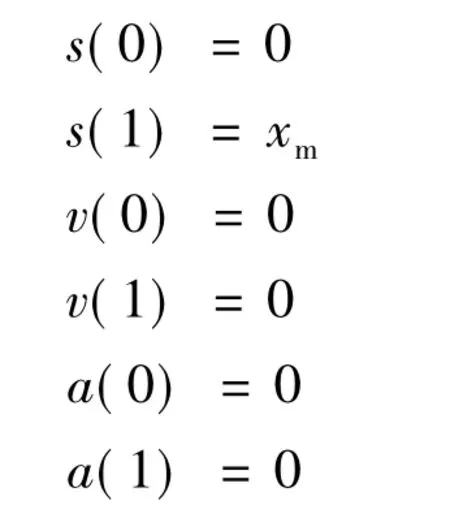
将边界条件代入位移函数、速度函数、加速度函数、加加速度函数即可得出各个参数及最终表达式:

优化后的曲线如图3～图6所示。

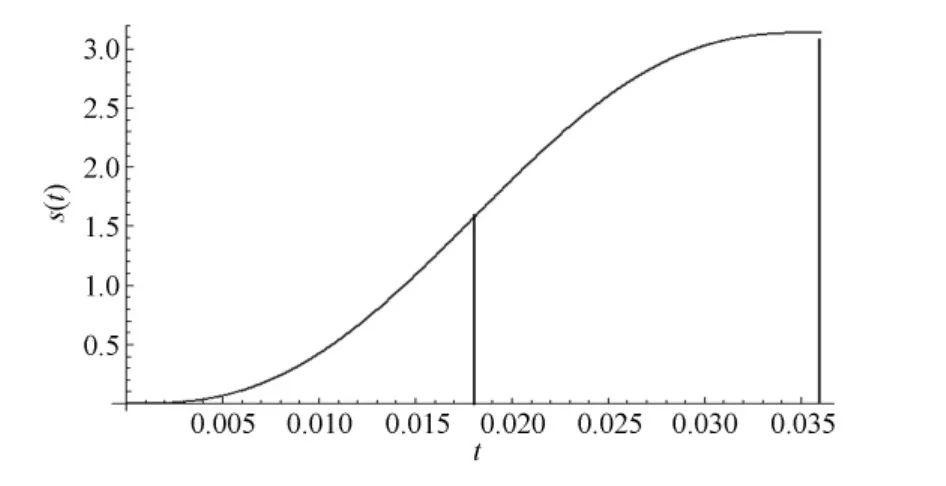
图3 优化后的位移曲线图

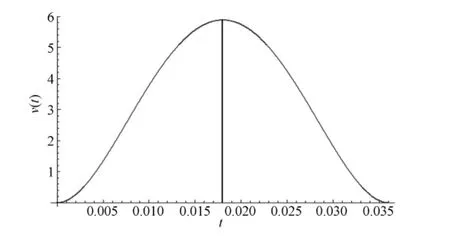
图4 优化后的速度曲线图

图5 优化后的加速度曲线图

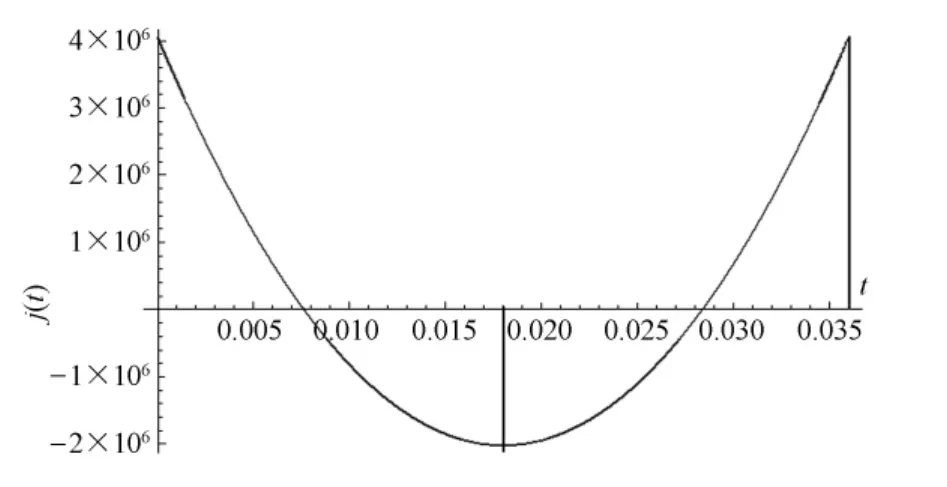
图6 优化后的加加速度曲线图

根据定义域可以计算出各函数的极值，即最大值:

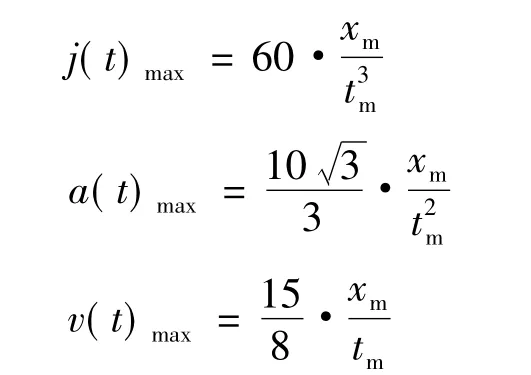
加速度与电机总力矩的关系式为:

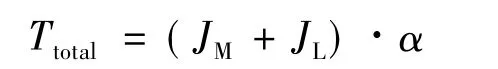
由速度、加速度、加加速度极值表达式可以看出，他们都是关于系统规定运行时间及位移的关系式，只要确定了系统的运行时间和位移，即可求出各自的最大值，为运动系统的控制提供方便。

另外，由加速度与电机总力矩的关系式可知，在电机惯量及负载惯量确定的情况下，只要确定加速度的值即可算出电机所需提供的转矩。与传统方法不同的是，这种方法算出来的加速度更加准确，更能满足设备柔性启停的要求。

3 分析对比

为检验优化后的加减速曲线对固晶臂末端位移响应的改善情况，本文通过ANSYS中瞬态动力学模块对两条曲线(传统的三角形加减速曲线和优化后的加减速曲线)加载情况进行了对比。

3.1 用传统的加减速曲线进行计算分析

由梯形或者三角形加减速曲线可知，固晶臂要在36ms内完成180°的旋转运动，其加速度计算如下:

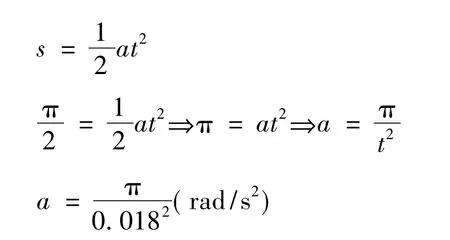
上述推导过程算出了前一半时间内加速度的值，此过程中固晶臂的角速度从零恒定地加速到最大速度。后一半时间内速度要从最大速度降为零，因此加速度方向与前一半时间的减速度的方向相反，大小不变。

驱动力矩T=ja，固晶臂的加速度为j=2×10－4kg·m2，因此传统加减速曲线力矩关于时间的表达式为:

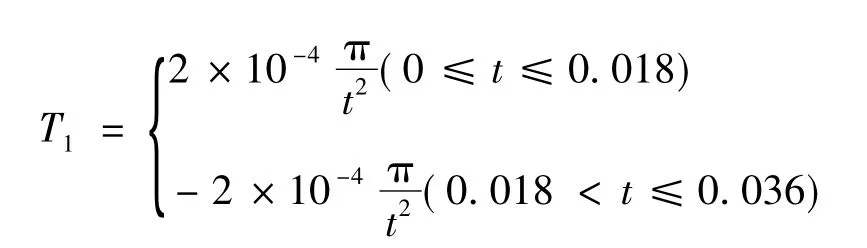
利用ANSYS瞬态动力学分析模块对固晶臂进行动力学瞬态分析，结果如图7所示。

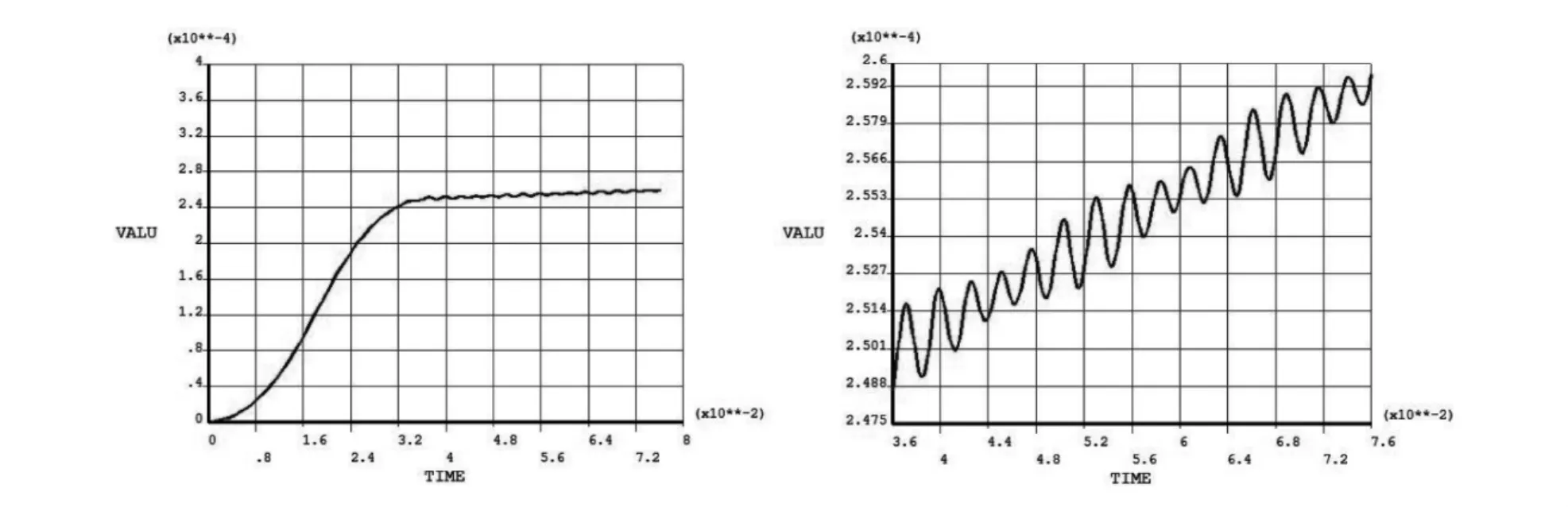
图7 采用传统加减速曲线加载时固晶臂末端位移响应情况

由图7可知从整体情况来看加载结束后固晶臂末端的位移已经没有大的变化，但是仍然可以看出，位移响应有上升的趋势。如果把时间轴细化到36ms到76ms这一段，则明显可以看出，固晶臂末端振动没有趋稳，还在呈现明显的上升趋势。

3.2 用优化后的加减速曲线进行计算分析

根据优化后的加减速曲线很容易得出驱动力矩关于时间的函数:

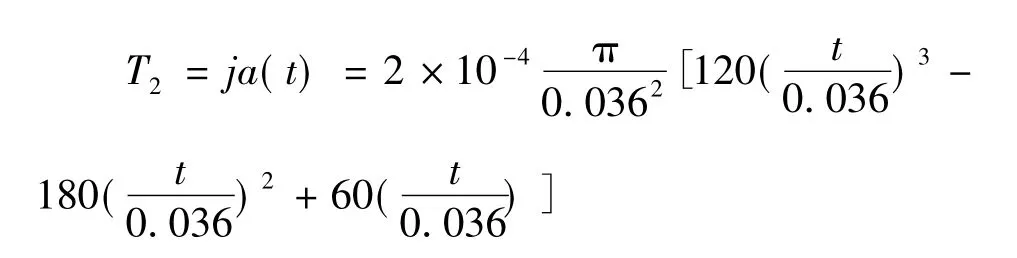
同样利用ANSYS瞬态分析模块对固晶臂进行瞬态动力学分析，结果如图8所示。

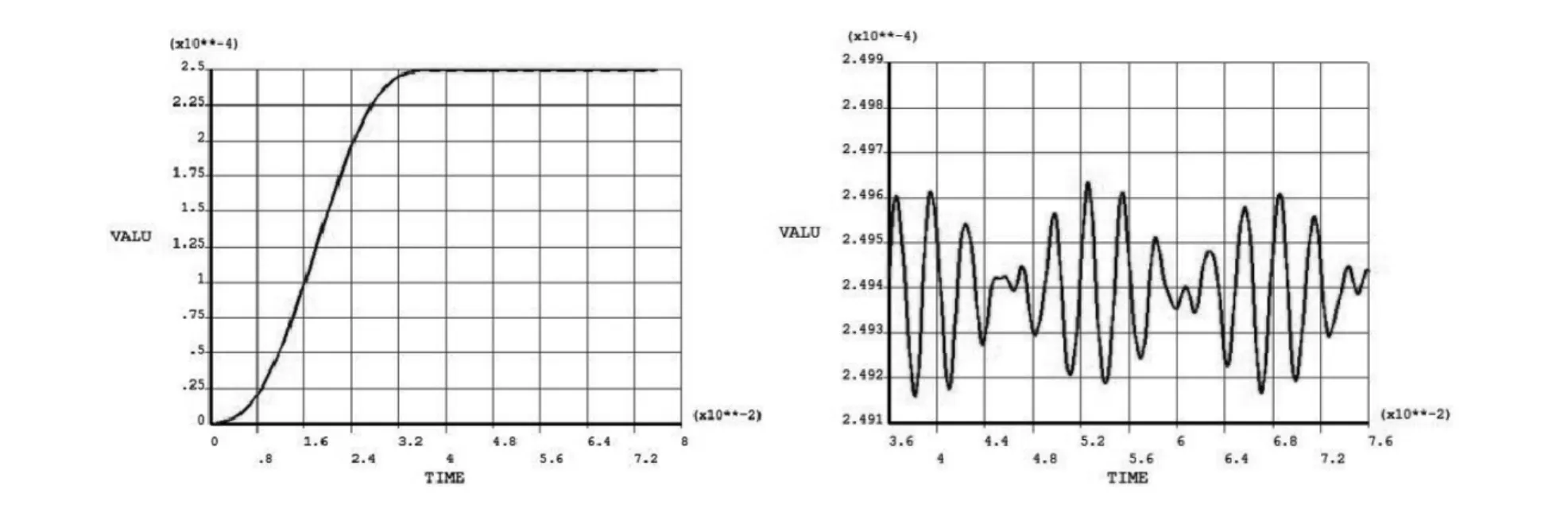
图8 采用优化后的加减速曲线加载时固晶臂末端位移响应情况

由图8可以看出整个计算分析时间内(0ms到76ms)，固晶臂的位移响应基本稳定，再将时间轴细化到36ms到76ms这一段，可以看出固晶臂的位移只在很小的范围内变化，已经基本趋稳。

通过对比分析可知，与传统的梯形或者三角形加速曲线相比，优化后的加速曲线对固晶臂末端位移响应有明显的改善，其趋稳时间大幅度缩短。

4 结束语

本文应用多项式拟合的方法构造出了五阶多项式的S曲线轨迹算法。在前人的基础上提出了更高阶的函数表达式、更准确的多项式，并结合LED粘片机的应用给出具体的函数表达式及函数图像，克服了传统梯形曲线的柔性不足问题，也避免了分段型S曲线给系统带来的复杂性问题，为LED粘片机等高速、高效、高精度设备的运行控制提供了新的更准确的S曲线控制算法。

［1］林晓新，吴小洪，曹占伦，等.S曲线在加减速控制在LED粘片机中的应用［J］.机械制造，2008，46(5):21 －23.

［2］郎平，郭东.COSMOS在LED粘片机拾取臂振动分析中的应用［J］.封装与测试，2011，40(5):21 －24.

［3］袁喜林，吴晓红，温颖.基于COSMOSworks的LED粘片机焊头机架优化设计［J］.制造业信息化，2008(9):106－107.

［4］陈友东，王田苗，魏洪兴，等.数控系统的直线和S曲线［J］.中国机械工程，2006，17(15):1600 －1603.

［5］李晓辉，邬义杰，冷洪滨.S形加减速控制方法的研究［J］.组合机床与自动化加工技术，2007(10):49－53.

［6］李丹.多项式拟合柔性加减速算法的研究［J］.制造业自动化，2010，33(3):158 －160.

A New S－curve Acceleration and Deceleration Algorithm Applied on LED Die－bonder

LIU Jing，WU Meiping
(Jiangnan University，Jiangsu Wuxi，214122，China)

The traditional acceleration/deceleration algorithm based on liner method and exponential method is not suitable for equipments of high－speed＆ high－precision，such as LED die－bonder because of the vibration caused by acceleration discontinuity affects.In order to solve this problem，it puts forward a new control method of fifth－degree polynomial acceleration/deceleration algorithm.Aiming at the LED die－bonder，it shows the function of displacement，speed，acceleration and jerk，introduces also the normalization form of the functions including the expression of maximum value of the functions.This algorithm supplies a reliable reference for acceleration/deceleration controlling and motor selection.

High－speed＆High－precision;Polynomial;Acceleration/deceleration;LED－bonder

TH113.2+2

A

2095－509X(2013)03－0078－04

10.3969/j.issn.2095－509X.2013.03.018

2012－11－08

刘静(1986—)，男，江苏泰州人，江南大学硕士研究生，主要研究方向为CAD/CAM。

DOI:10.3969/j.issn.2095－509X.2013.03.019