气动钉枪橡胶缓冲垫的动力学仿真分析

陈中哲，章巧芳，彭 伟

(特种装备制造与先进加工技术教育部/浙江省重点实验室(浙江工业大学)，浙江杭州 310014)

气动钉枪橡胶缓冲垫的动力学仿真分析

陈中哲，章巧芳，彭 伟

(特种装备制造与先进加工技术教育部/浙江省重点实验室(浙江工业大学)，浙江杭州 310014)

为得到气动钉枪橡胶缓冲垫的动态应力等响应，以气动钉枪实测的压力作为边界条件，利用非线性动力学分析软件LS－DYNA对橡胶缓冲垫承受枪针组件冲击的动态过程进行了数值模拟研究。仿真结果得到的最大应力出现部位与缓冲垫实际破坏位置有较好的一致性。还进行了高速摄像实验，实验结果与仿真结果的对比验证了仿真的可靠性。

气动钉枪;橡胶缓冲垫;动力仿真;高速摄像

气动钉枪作为一种典型的手持式气动工具，已被广泛应用于建筑装潢、制造包装等行业。工作过程中枪体底部的橡胶缓冲垫承受枪针组件的冲击，起缓冲的作用。由于承受连续的冲击载荷，使橡胶缓冲垫成为气动钉枪的易损零件。目前，国内钉枪企业所用的橡胶缓冲垫寿命较短，因而直接影响了气动钉枪整枪的寿命。

本文采用动力学数值模拟方法，利用LS－DYNA软件，对气动钉枪橡胶缓冲垫承受活塞冲击的动态过程进行了研究，为后续的结构改进和提高缓冲垫寿命提供理论指导。

1 气动钉枪的冲击系统

气动钉枪是一种以高压气体为动力源的气动工具，其结构如图1所示。活塞和枪针通过螺纹配合构成枪针组件。当扣动扳机时，高压气体快速进入活塞上端气缸，将压力作用在活塞上表面，此时活塞下端流场气体压力与大气相同。由于活塞上端的作用力p1大于下端作用力p2，在二者的压力差的驱动下枪针组件高速运动［1］。随着活塞的下移，气缸下部流场空间减小，气体压力增大。当活塞到达下端时，缓冲垫对其起到缓冲作用。在活塞的作用力下，缓冲垫被压缩产生径向变形，而缓冲垫的径向变形将受到气缸的约束作用。

在活塞撞击缓冲垫的过程中，涉及到活塞对缓冲垫的动态冲击、橡胶材料的非线性、各零件之间的接触非线性等问题，很难用解析的方法对橡胶缓冲垫的受冲击特性进行分析，同时缓冲垫位于枪体内部，用实验的方法对其进行分析较为困难。因此采用动态非线性有限元软件LS－DYNA对其进行数值模拟分析。

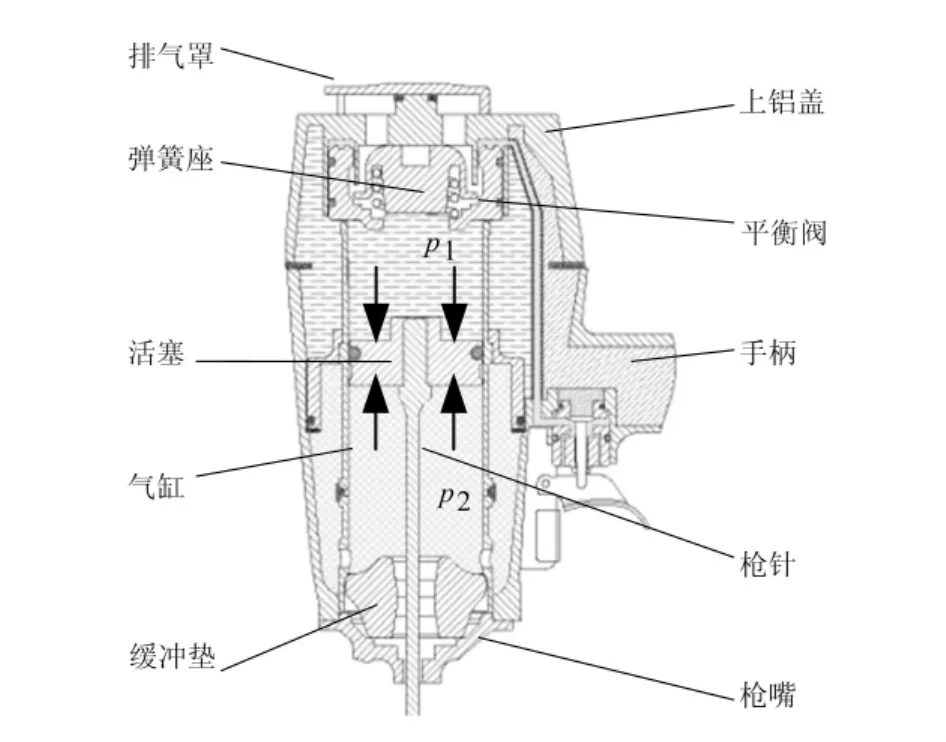
图1 气动钉枪结构示意图

2 模型的建立与网格划分

橡胶缓冲垫与其他零件的装配关系如下:缓冲垫底部紧贴在枪嘴上表面，顶部在工作状态下承受来自枪针组件的冲击力，侧面与气缸接触。由于缓冲垫在工作过程中只与枪嘴、枪针组件及气缸有直接关系，因此分析中只建立这些零件的装配体，然后对该装配体进行分析，并在不影响计算结果的条件下，对枪嘴、枪针组件和气缸中不与缓冲垫接触的部分做几何简化处理，同时在三维造型软件Pro/E中建立几何模型。

将建立好的几何模型导入软件Hypermesh中进行网格划分，划分好的六面体网格模型如图2所示。

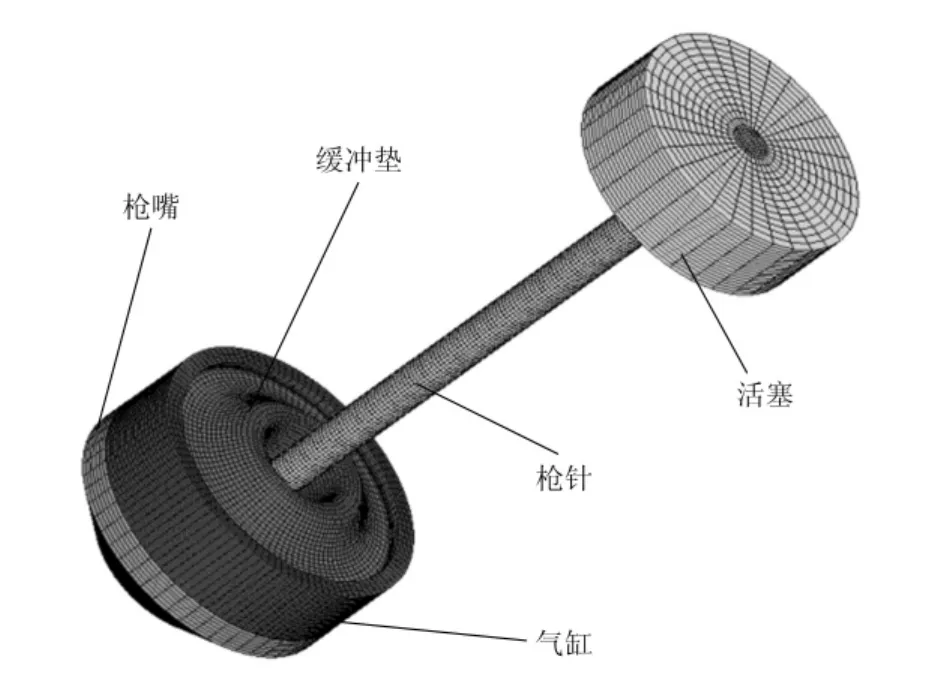
图2 仿真分析网格模型

3 材料模型

橡胶材料属高分子聚合物材料，是一种各向同性的体积近似不可压缩材料。研究表明，橡胶材料的力学行为主要表现为准静态超弹性(非线性弹性)与动态粘弹特性(应变率相关性)［2］。描述超弹性材料特性的理论之一是基于应变能密度函数的大弹性变形本构理论，目前得到广泛承认并在工程中大量应用的主要是广义Mooney－Rivlin应变能密度函数［3］。橡胶不仅具有高弹特性，而且其力学行为是与应变率相关的，即具有粘弹性［4］。Yang L M和Shim等［5］对高应变率下橡胶的本构响应进行了理论和实验研究。由于活塞撞击缓冲垫的载荷为冲击载荷，需考虑应变率的影响。综合考虑求解需要和实验条件，最终选取考虑简单应变率效应的橡胶粘超弹性材料模型来模拟橡胶材料，即LS－DYNA中的77号材料模型*MAT_HYPERELASTIC_RUBBER。该模型用2参数Mooney－Rivlin模型来表征橡胶的超弹性部分，通过对标准试件的单轴压缩实验来获取该橡胶材料压缩的应力应变曲线(如图3所示)，然后将该曲线输入到关键字文件中。对于橡胶的粘弹性部分，该材料模型考虑简单的速率效应，通过实验获取所需的应力松弛曲线，并输入到关键字文件中，应力松弛曲线如图4所示。

对于枪嘴、气缸、枪针组件，由于其材料为刚性材料且变形量小，而且是非主要关心区域，因此将其处理为刚体，以便简化计算。

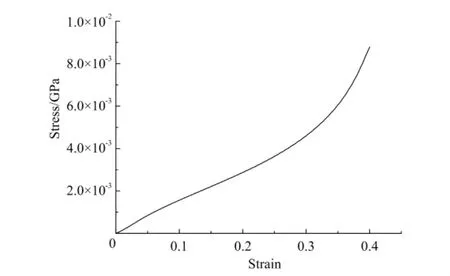
图3 压缩应力－应变曲线

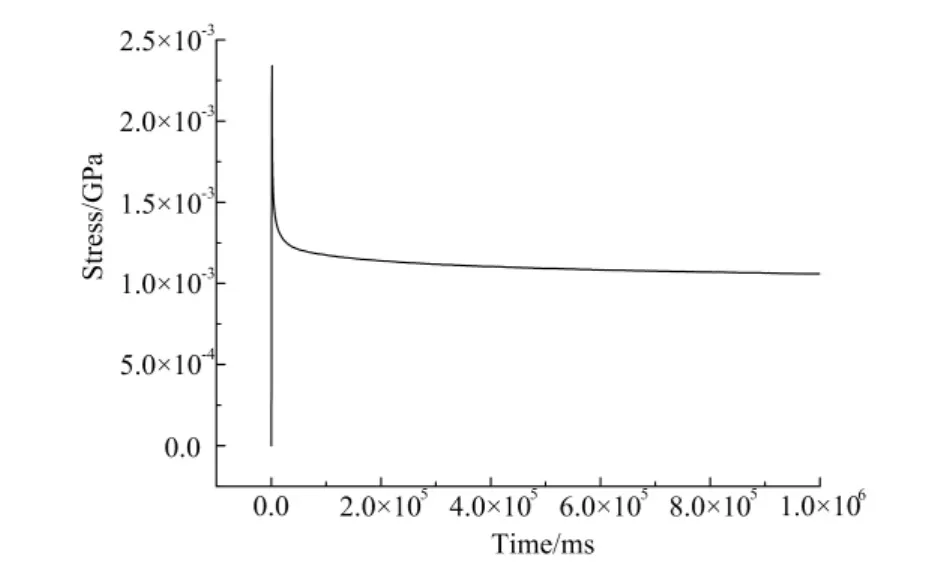
图4 应力松弛曲线

4 边界条件

气动钉枪工作时，实际的工况为活塞在上下端气体压力差的作用下撞击缓冲垫，因此如果要模拟实际的工况，需知在整个撞击过程中活塞上下端气体压力随时间变化的曲线。通过在枪体上进行相应的位置开孔，并安装PCB动态压力传感器。通过实验测得活塞上端气体压力随时间变化的曲线如图5所示，活塞下端气体压力随时间变化的曲线如图6所示。将实测压力曲线作为边界条件施加于活塞的有限元模型。由于枪嘴和气缸相对于活塞静止，故将枪嘴和气缸作为固定边界条件处理。

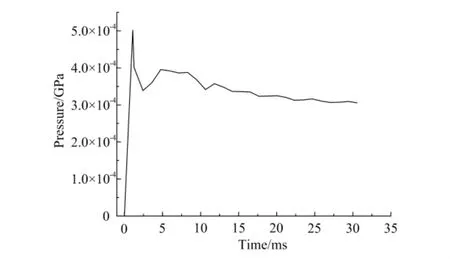
图5 活塞上端气体压力随时间变化曲线

缓冲垫工作状态下与气缸、枪嘴、枪针组件发生接触，因此分别创建缓冲垫与气缸、缓冲垫与枪嘴、缓冲垫与枪针组件这3对接触边界条件。

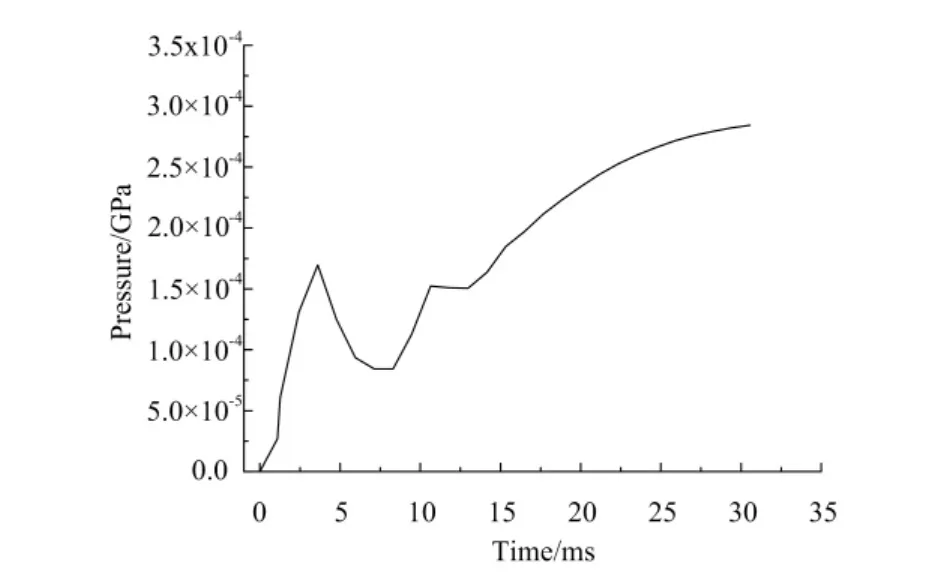
图6 活塞下端气体压力随时间变化曲线

5 仿真结果与分析

对相关求解参数进行控制，利用LS－DYNA求解器对有限元模型进行求解。图7所示为活塞位移随时间的变化曲线。由图7可以看出，活塞的位移经历了3个波峰最后趋于平衡。第一个波峰值最大，第二、第三个波峰值依次减小。由气动钉枪的工作原理可知，活塞与缓冲垫经若干次碰撞后将紧贴在缓冲垫上。通过测量气动钉枪几何模型，得到活塞从初始位置至刚接触缓冲垫而没有发生挤压变形时的行程为117mm，即为图中位移曲线趋于平衡的位置。之前有3个波峰均大于117mm，由此可知，活塞对缓冲垫总共碰撞挤压了3次，第一个波峰即为第一次碰撞压缩的最大压缩量，波峰值125mm减去平衡位置117mm即为缓冲垫的最大压缩量8mm，发生在活塞运动进程t=8.0ms时刻。经过第一次碰撞，在橡胶缓冲垫弹力的作用下活塞被弹回，离开缓冲垫，但此时活塞上下表面仍有压力差的作用，在压力的作用下活塞向后回弹的速度快速衰减为0，并向缓冲垫发起第二次撞击。第二次碰撞缓冲垫的最大压缩量为3.5mm，发生在15.9ms时刻。依次类推将有第三次撞击，缓冲垫被压缩了1mm，发生在23.7ms时刻。由于活塞上下表面的压力逐渐趋于相等，所以活塞经过3次碰撞后将趋于平衡，紧贴在缓冲垫上表面不再运动，此时气动钉枪进入缓冲阶段的尾声。

活塞第一次撞击缓冲垫的碰撞压缩能量最大，因此较大的应力也都集中在第一次压缩过程中。由于缓冲垫结构、受载和边界的对称性，应力分布也是轴对称的。可用过中心轴的二维平面观察缓冲垫的应力分布。图8所示为缓冲垫第一次压缩过程中3个时刻的等效应力云图。

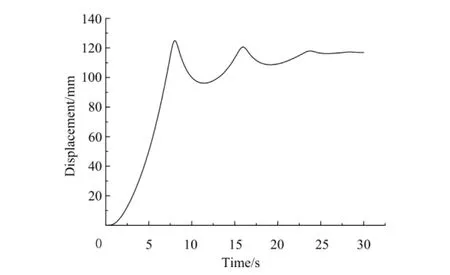
图7 活塞位移随时间变化曲线

图8(a)、(b)、(c)分别为活塞运动进程中3个不同时刻缓冲垫的等效应力分布云图。图8(c)为最大等效应力出现时刻缓冲垫等效应力的分布，最大等效应力为19.17MPa，发生在活塞运动进程t=8.0ms时刻，发生的位置为缓冲垫内侧中部偏上位置。最大等效应力出现的时刻与缓冲垫达到最大压缩量的时刻恰好相同。最大应力出现的位置可以视为橡胶缓冲垫的危险位置。图9(a)为碰撞过程中缓冲垫达到最大等效应力时刻应力分布的三维图，通过把最大等效应力出现的位置与图9(b)中实物橡胶缓冲垫的实际破坏位置进行对比，发现最大应力出现的位置与缓冲垫实际破坏位置两者有较好的一致性。

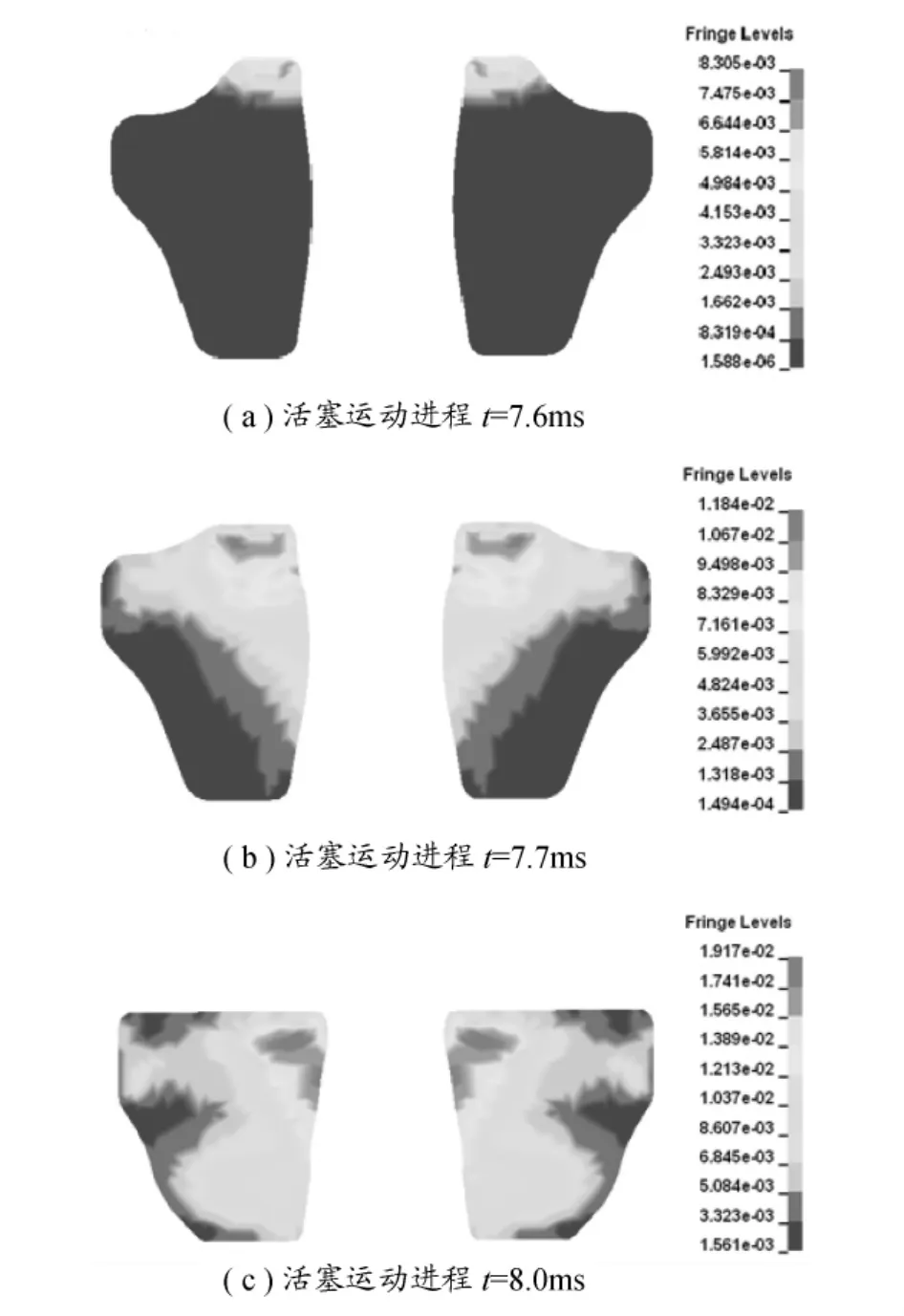
图8 3个不同时刻缓冲垫的等效应力云图

图9 缓冲垫最大等效应力出现位置与实际破坏位置对比图

6 实验验证与分析

为了验证仿真结果的可靠性，设计实验方案，通过高速摄像实验可获得实际枪针组件(活塞)位移随时间变化的曲线，并将由实验得到的活塞位移随时间变化曲线与由仿真得到的活塞位移随时间变化曲线进行对比。

采用切除枪嘴头部和加长枪针的处理方法，使得枪针在初始位置时就已露出枪嘴，因此枪针组件的整个运动过程都能被高速摄像仪捕捉到。搭建好的实验平台实物图如图10所示。

图10实验平台实物图

通过将高速摄像实验拍摄到的视频文件进行后处理，可得到活塞位移随时间变化的曲线，再将该曲线与仿真得到的活塞位移随时间变化曲线进行对比(如图11所示)。

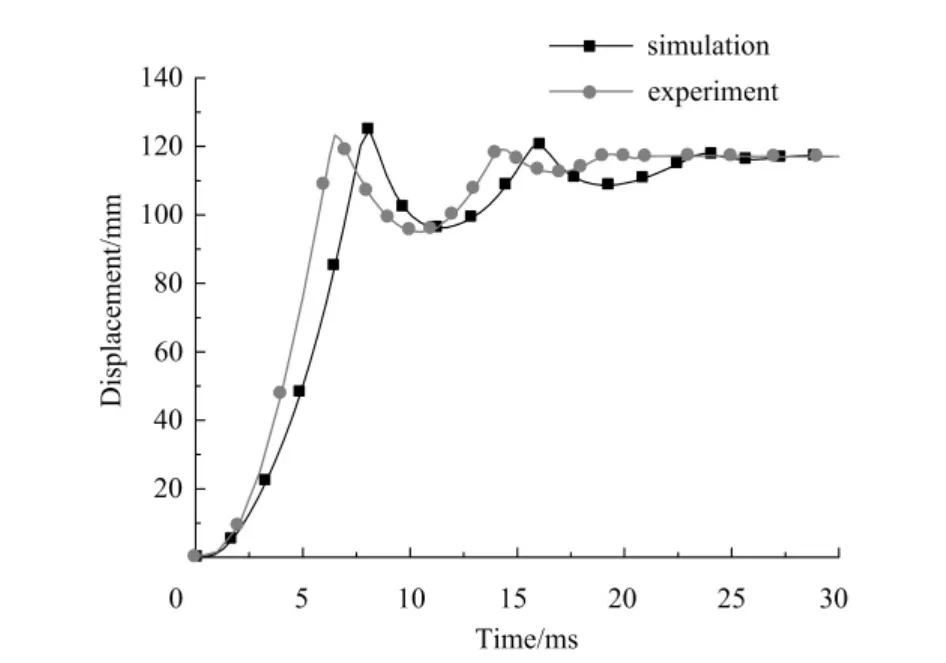
图11 活塞位移随时间变化仿真与实验对比图

通过实验得到的活塞位移曲线也是经历了3个波峰后趋于平衡，与仿真分析的结果在形状趋势上有较好的一致性，从而验证了仿真分析的可靠性。

而实验曲线与仿真曲线两者也存在着差异。首先，通过实验得到的曲线的3个峰值均小于仿真曲线，实验中缓冲垫最大压缩量为6.23mm，小于仿真的最大压缩量8mm。由于选择的橡胶材料模型只考虑简单的应变率效应，所以无法精确模拟材料在高应变率下的行为，这很可能是导致由仿真得到的缓冲垫最大压缩量在数值上大于由实验得到的缓冲垫最大压缩量的主要原因。仿真与实验的另一个差异表现为，仿真得到的位移曲线在时间上滞后于实验获得的曲线。由于在获取仿真需要的压力边界条件时，施加在活塞上的压力为气缸内部的压力，而气缸内部的压力是通过1根圆管引出测得，当气体到达传感器位置时必然存在损耗和延时，这使得加在仿真模型上的压力边界条件与真实情况仍然存在着差异，这种差异很可能就是导致2条曲线在时间上存在一个滞后量的原因。

7 结束语

本文利用动态压力传感器测得了活塞上下端的压力随时间变化的曲线，并将其作为边界条件。运用非线性动力学有限元软件LS－DYNA对橡胶缓冲垫承受枪针组件冲击的动态过程进行了仿真分析，得到了整个冲击过程中橡胶缓冲垫的最大压缩量和缓冲垫的动态应力等响应，并得到了最大应力出现时刻的应力分布云图，其中最大应力出现部位与缓冲垫实际破坏位置有较好的一致性。通过高速摄像实验对仿真结果的可靠性进行了验证，为后续缓冲垫结构的优化提供了理论依据。

［1］毕向秋.气动钉枪流场数值模拟及气动性能分析研究［D］.杭州:浙江工业大学，2007.

［2］周相荣，王强，王宝珍.一种基于Yeoh函数的非线性粘超弹本构模型及其在冲击仿真中的应用［J］.振动与冲击，2007，26(5):33－37.

［3］Charlton D J，Yang J，Teh K K.A review of methods to characterize rubber elastic behavior for use in finite element analysis［J］.Rubber Chemical and Technology，1994，67(3):481 －503.

［4］Johnson A R，Quigley C J.A viscohyperelastic Maxwell model for rubber viscoelasticity［J］.Rubber Chemistry and Technology，1992，65(1):137－153.

［5］Yang L M，Shim V P W，Lim C T.Visco－hyperelastic approach to modeling the constitutive behaviour of rubber［J］.International Journal of Impact Engineering，2000，24(6):545－560.

The Dynamic Simulation Analysis of Pneumatic Nail Gun's Rubber Buffer

CHEN Zhongzhe，ZHANG Qiaofang，PENG Wei
(Zhejiang University of Technology，Zhejiang Hangzhou，310014，China)

In order to obtain the information about the dynamic stress of the nail gun＇s rubber buffer，it uses the measured pressure of pneumatic nail gun as the boundary condition，realizes a numerical simulation of the dynamic process based on the non－linear dynamic software LS－DYNA.The simulation result shows the actual failure position of the rubber buffer.Furthermore，it designs the high－speed vedio experiment.The comparison between the experimental results and simulation results verify the reliability of the simulation.

Pneumatic Nail Gun;Rubber Buffer;Dynamic Simulation;High－speed Vedio

TP29

A

2095－509X(2013)03－0018－04

10.3969/j.issn.2095－509X.2013.03.004

2012－08－29

陈中哲(1988—)，男，浙江金华人，浙江工业大学硕士研究生，主要研究方向为有限元仿真。