基于双寡头竞争回收的多级再制造逆向供应链定价策略研究

周占峰

(西北工业大学机电学院，陕西西安 710072)

基于双寡头竞争回收的多级再制造逆向供应链定价策略研究

周占峰

(西北工业大学机电学院，陕西西安 710072)

针对双寡头回收商、单一制造商、单一零售商所构成的多级逆向供应链，运用博弈论研究了再制造逆向供应链的定价问题。考虑双寡头回收商之间的不同竞争模式，分别建立了博弈模型，并给出了相应的最优定价策略。依据最优定价策略对不同竞争模式下回收商、制造商、零售商以及逆向供应链的最大利润进行求解并进行了比较。结果表明:当双寡头回收商结成回收联盟时，回收商的利润增加，但制造商、零售商以及整个逆向供应链的利润都会减少。

再制造;逆向供应链;博弈论;定价

1 问题描述及假设条件

再制造产品回收模式主要有3种:制造商负责回收、零售商负责回收、制造商委托第三方负责回收［11］，本文选择专业的第三方负责回收模式，建立两个回收商、单一制造商、单一零售商的逆向供应链，考虑逆向供应链不同节点间的非合作博弈Stackelberg模型。其决策过程如下:制造商根据市场调查和需求分析制定废旧产品回收计划，然后确定从回收商处回收废旧产品的价格，以最大化自己的利润，回收商在观测到制造商的决策后制定从顾客手中回收废旧产品的回收价格，以最大化自己的利润。零售商在观测到这些信息后确定批发价格以最大化自己的利润。文中所使用的相关符号及说明如下:分别为非合作与合作回收下第i个回收商从顾客手中回收废旧产品的价格，为回收商的决策变量;Cr为回收商的单位废旧产品回收成本，包括运输成本、检测成本等;w1，分别为非合作与合作回收下制造商从回收商处回收废旧产品的价格，为制造商的决策变量;分别为非合作与合作回收下制造商销售给零售商的再制造产品批发价格，为制造商的决策变量;Cm为制造商的单位废旧产品的再制造成本;Cs为零售商的单件再制造产品的销售成本;P为销售商出售给客户的再制造产品的销售价格，为确定常量。分别为第i个回收商废旧产品的回收量;pri，分别为非合作与合作回收下第i个回收商的利润;分别为非合作与合作回收下制造商的利润;分别为非合作与合作回收下零售商的利润;分别为非合作与合作回收下逆向供应链的总利润。

为了便于模型求解，做出基本假设如下:(1)回收商、制造商和销售商都是在信息完全对称、风险中性的条件下做出决策，回收商、制造商和零售商都是完全理性的，决策的目标是使其各自的利润最大化;(2)所有回收产品回收成本相同且都可以用于再制造，所有再制造产品都可以销售;(3)两个回收商的边际回收成本相同，都为Cr;(4)回收商通过回收必须获利，即w1－Pri－Cr＞0;(5)制造商通过再制造必须获利，即w2－w1－Cm＞0;(6)零售商通过回收必须获利，即P－w2－Cs＞0;(7)回收商的回收量除了和自己的回收价格有关以外，还和竞争对手的回收价格有关，且是自己回收价格的线性增函数、是竞争对手回收价格的线性减函数，可表示如下:

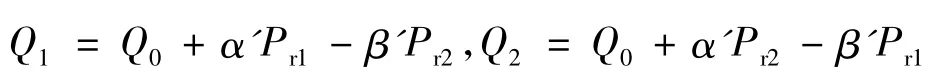
其中:Q0为不依赖价格的基本回收量，反映顾客的环保意识，Q0＞0;α为价格弹性系数，为确定常量;β为回收替代系数，是确定常量，反映顾客对价格比较的敏感性程度，α＞β＞0。

根据上述假设，两个回收商、制造商以及零售商的利润可以表示如下:

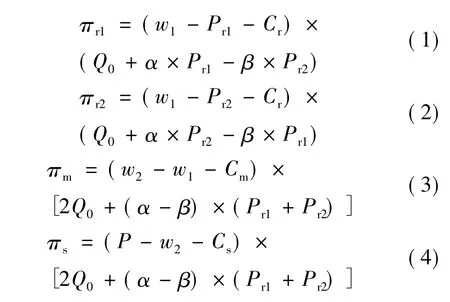
2 回收商分散决策下的定价策略

在两个回收商进行分散决策的情况下，逆向供应链的博弈分为两个部分:逆向供应链各个节点(回收商、制造商、零售商)为完全信息下的动态博弈，选择建立Stackelberg博弈模型;两个回收商之间为完全信息下的非合作静态博弈，选择建立伯川德双寡头垄断竞争模型。该博弈的具体过程为:首先制造商确定从回收商处回收的废旧产品的价格，两个回收商在得到制造商的信息后同时确定从顾客手中回收废旧产品的价格，零售商在获取制造商和回收商的决策信息后制定再制造产品的批发价格。在这些决策制定以后，制造商和零售商分别按既定的回收价格回收废旧产品。为求得Stackelberg均衡解，首先要求出该博弈的第二阶段反应函数，即回收商得知Pm以后，确定Pri以最大化自己的利润。在式(1)中对Pr1求偏导，在式(2)中对Pr2求偏导，结果如下:

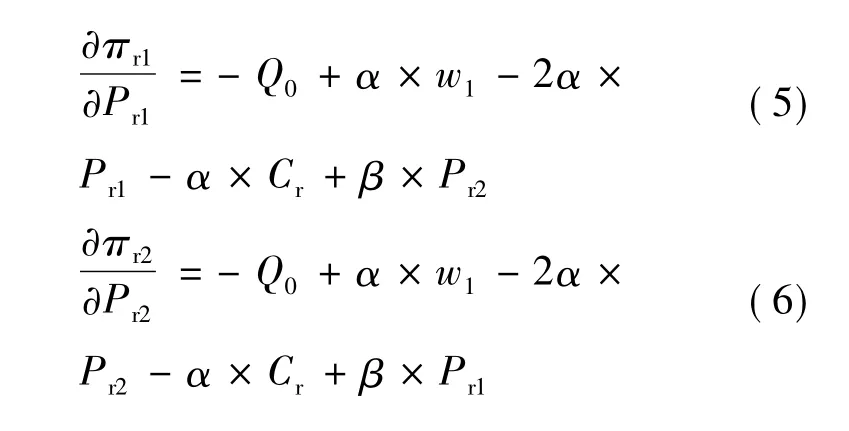
将式(10)、(11)、(12)分别代入式(1)、(2)、(3)、(4)，得到回收商、制造商、零售商以及逆向供应链系统的最大利润分别为:

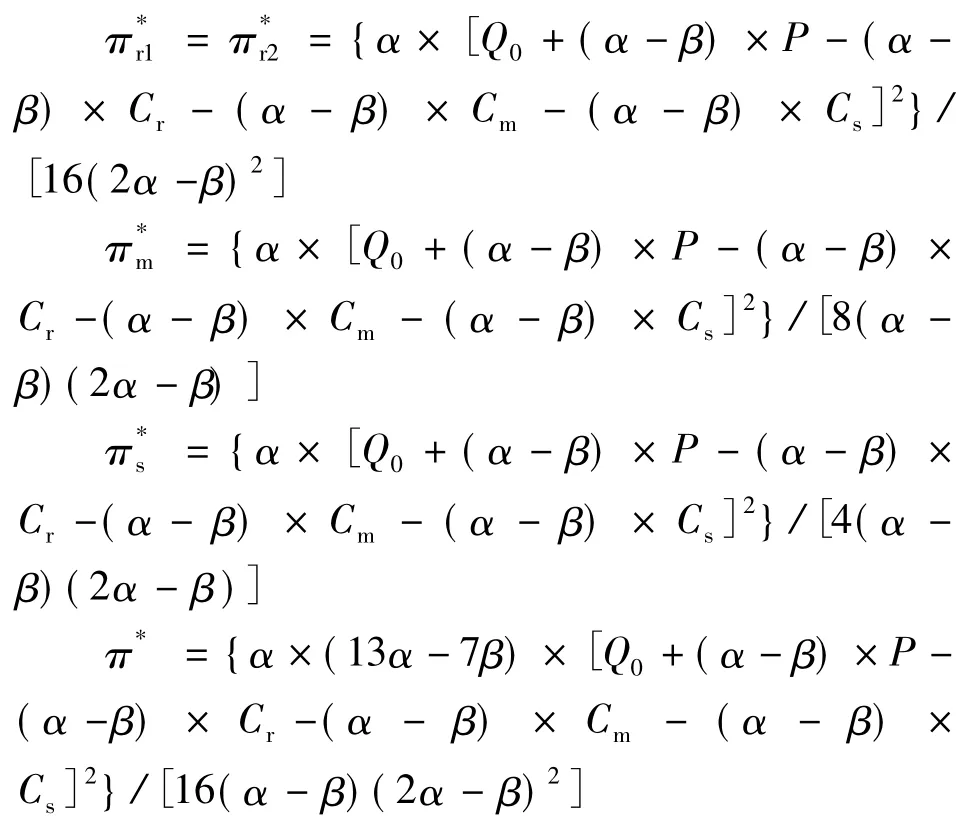
3 回收商联盟下的定价策略

在回收商联盟下，两个回收商建立联盟对废旧产品进行回收，逆向供应链的博弈仍然分为两个部分，所不同的是在逆向供应链博弈的第二阶段，两个回收商之间的竞争属于完全信息下的合作博弈，即回收商在获取制造商的价格信息后，统一对回收价格进行决策，其目标是使回收联盟的总利润最大，回收联盟的总利润可以表示如下:

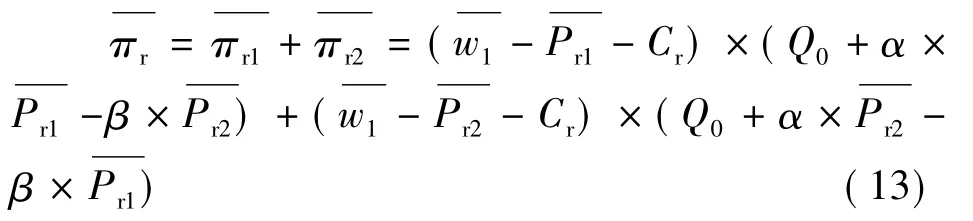
最优定价和最大利润的求解过程与分散回收决策一致，不再详述。得到回收商联盟下的最优定价为:

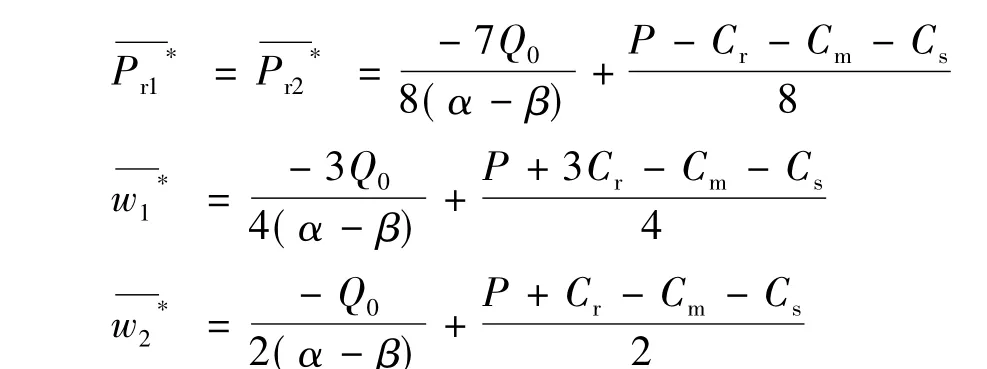
此时，回收商、制造商、零售商的最大利润以及逆向供应链最大总利润分别为:

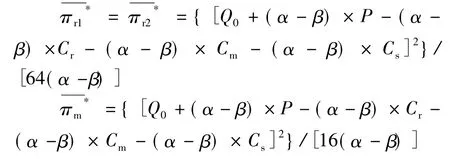
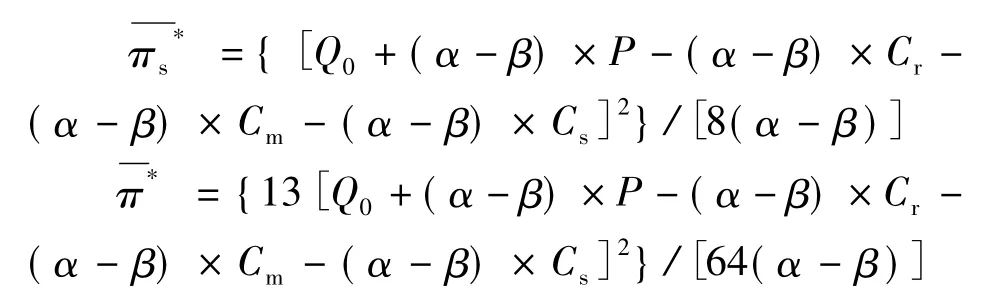
4 不同回收决策下的定价策略比较

通过比较分散回收决策与回收商联盟下的定价策略得出以下结论。

结论1:回收商联盟下，回收商会合谋降低从顾客手中回收废旧产品的价格。

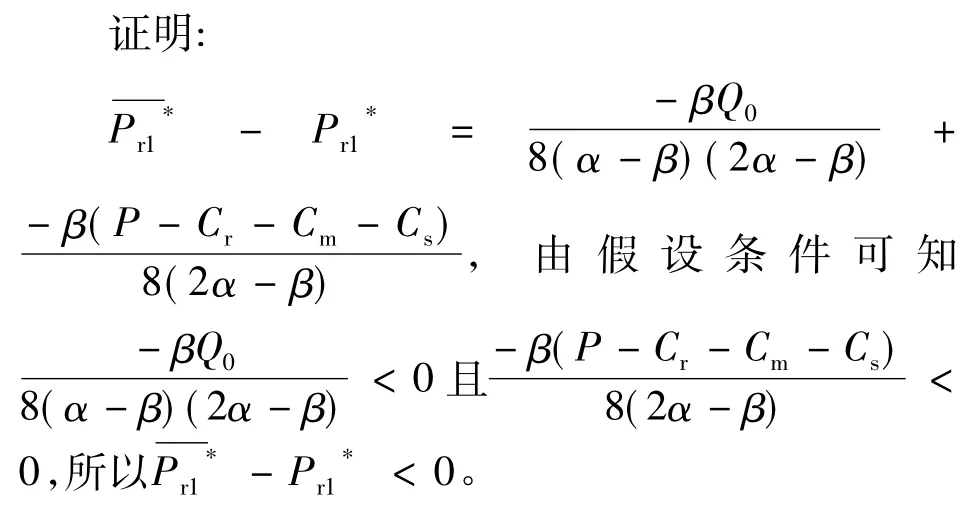
结论2:回收商联盟下两个回收商的利润增加，制造商、销售商以及系统总利润减少。

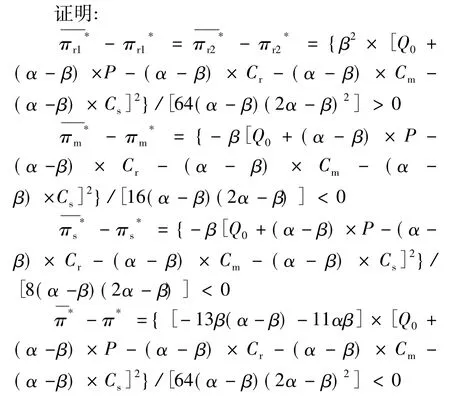
由上述结论可知，当双寡头回收商结成回收联盟时，回收商的利润提高，但制造商、零售商以及整个逆向供应链的利润都会降低，因此在以制造商为主导的逆向供应链中要避免多个回收商结成垄断联盟，同时为了不影响回收商的利益，要运用一定的协调策略对整个逆向供应链的利润进行协调分配。

5 结束语

产品回收是再制造逆向供应链中非常重要的一个环节，逆向供应链中各个阶段的合理定价将直接影响各个企业的利益，决定整个再制造逆向供应链能否顺利实施。由双寡头回收商负责回收的逆向供应链中，回收商之间通常会建立回收联盟来降低废旧产品回收价格，进而提高其利润，而制造商和销售商的利润会降低，逆向供应链也不可避免地存在着效率损失。实践中，多回收商回收的逆向供应链较为普遍，本文的研究可以为解决多回收商竞争回收的逆向供应链定价和协调问题提供理论上的指导，促进再制造逆向供应链的建立、运行和发展。但是，本文所研究的多级逆向供应链仅仅考虑到双寡头竞争回收的情况，对于多回收商、多零售商所组成的复杂逆向供应链的定价以及利益协调策略将是下一步研究的方向。

［1］李婷.博弈论在逆向供应链系统定价中的应用［J］.物流技术，2007，26(5):80 －83.

［2］徐滨士.再制造工程及其关键技术［J］.内燃机与配件，2009(4):3－8.

［3］罗海波，李帮义，刘元元.基于博弈的逆向供应链定价及利益分配研究［J］.价值工程，2009(4):4－7.

［4］高举红，金晨赫.废旧产品回收再制造逆向供应链的定价策略研究［J］.物流工程与管理，2010，32(11):76 －79.

［5］顾巧论，季建华.基于模糊回收价格的逆向供应链定价策略研究［J］.信息与控制，2006，35(4):417 －422.

［6］孙多青，马晓英.基于博弈论的多零售商参与下逆向供应链定价策略及利润分配［J］.计算机集成制造系统，2012，18(4):867－874.

［7］肖忠东，查仲鹏，徐琛.寡头垄断模式下废旧产品回收定价的比较研究［J］.科技进步与对策，2011，28(3):113 －116.

［8］李响，李勇建，蔡小强.随机产率和随机需求下再制造系统的回收定价决策［J］.系统工程理论与实践，2009，29(8):19－27.

［9］张克勇，周国华.基于博弈论的闭环供应链差别定价协调问题［J］.经济问题，2008(9):13－15.

［10］王文宾，达庆利.零售商与第三方回收下闭环供应链回收与定价研究［J］.管理工程学报，2010，24(2):130 －134.

［11］魏洁，李军.EPR下的逆向物流回收模式选择研究［J］.中国管理科学，2005(6):18－22.

Research on Pricing Strategy of Multi-level Remanufacturing Reverse Supply Chain Based on Duopoly Recovery Competition

ZHOU Zhanfeng
(Northwestern Polytechnical University，Shaanxi Xi＇an，710072，China)

By using the game theory，it studies the pricing problem in multi－ level remanufacturing reverse supply consisted of duopoly recycler，single manufacturer and single retailer.Considering the different competitive mode between the duopoly recyclers，it establishes the game model respectively and proposes the corresponding optimal pricing strategy.According to the optimal pricing strategy，the profit of recycler，manufacturer，retailer and reverse supply chain in different competitive mode are solved and compared.The results show that recycler＇s profit is raised，but the profit of manufacturer，retailer and reverse supply chain is reduced when duopoly recyclers form a recycling coalition.

Remanufacturing;Reverse Supply Chain;Game Theory;Pricing

F252

A

2095－509X(2013)03－0026－04

10.3969/j.issn.2095－509X.2013.03.006

传统的正向供应链是包括从原材料供应商、制造商到零售商的供需链，逆向供应链是从消费者手中回收废旧物品进行分类、检测、拆解，直到最终被处置的一系列过程［1］。为了解决日益严重的资源短缺、环境污染问题，各个国家纷纷采取发展循环经济、实现可持续发展的策略。逆向供应链通过废旧资源的回收利用可以提高资源的利用率，降低污染，因此受到各个国家的重视。再制造是逆向供应链的一种较为复杂的类型，是指以产品全寿命周期设计和管理理论为指导，以实现废旧物品性能提升为目标，以优质、高效、节能、节材、环保为准则，以先进技术和产业化生产为手段，进行修复、改造废旧产品的一系列技术措施或工程活动的总称，也被称为“绿色再制造”［2］。通过再制造不仅可以降低企业生产成本，提高经济效益，还可以有效减少废物排放，提高资源利用率，更好地保护生态环境。

逆向供应链各个环节中的定价问题不仅影响到各个企业的利润，也直接决定了整个供应链的效益，因此引起了众多学者的广泛关注。罗海波应用博弈理论，研究了单一制造商和两个零售商组成的逆向供应链系统，给出了合作与不合作博弈下的最优定价策略［3］。高举红在构建单一制造商和两个零售商的逆向供应链基础上，考虑了回收努力水平对定价的影响，给出了相应的定价策略［4］。顾巧论针对单一制造商和单一零售商的逆向供应链系统，将回收价格看作三角模糊数，应用模糊理论和博弈理论对回收价格浮动的基准点进行决策，给出了合作与非合作博弈下的均衡解［5］。李婷基于单一制造商和单一零售商构成的逆向供应链系统，应用博弈论对废旧产品回收的定价策略进行研究，分别得出了非合作博弈和合作博弈的均衡解［1］。孙多青运用Stackelberg博弈理论研究了多个零售商参与的逆向供应链的定价问题，求出了非合作与合作博弈下的最优定价策略，并利用改进的K－S解法对合作博弈下的供应链总利润进行了分配［6］。肖忠东以Mukhopadhyay模型为基础，在博弈和合谋两种不同条件下构建了定价模型，分析了回收定价决策中的各种影响因素，比较了博弈和合谋下的收益［7］。李响针对再制造逆向物流系统，考虑了随机产率和随机需求，建立废旧产品回收的最优定价模型［8］。张克勇运用博弈论对一个制造商和一个零售商组成的闭环供应链差别定价协调问题进行了研究［9］。王文宾基于市场细分建立了零售商回收与第三方回收废旧产品情形的闭环供应链决策模型，通过对两种情形决策变量的求解与比较，讨论了回收努力程度和产品定价的区别，分析了制造商与零售商的利润随消费者偏好系数的变化规律［10］。关于再制造逆向供应链的定价策略问题，不同学者从不同角度综合运用博弈论、经济理论、优化理论进行了研究，但目前研究的对象主要是针对单一制造商、单一零售商所组成的二级逆向供应链，供应链结构简单，缺乏实际应用性。文献［10］虽然考虑了三级逆向供应链，但针对的是单一回收商，没有考虑到回收商之间的竞争关系对于逆向供应链定价的影响。本文在相关文献研究的基础上，针对双寡头回收商、单一制造商、单一零售商所组成的三级逆向供应链，研究回收商之间不同竞争模式下逆向供应链的最优定价策略以及最大利润问题。

2012－08－30

陕西省教育厅科研专项基金资助项目(09JK124)

周占峰(1980—)，男，安徽蚌埠人，西北工业大学博士研究生，西安工业大学讲师，主要研究方向为供应链管理、管理信息化。