一类Dirichlet边值问题多解的存在性
2013-09-12买阿丽卢永红孙国伟
买阿丽,卢永红,孙国伟
(1.运城学院应用数学系,山西 运城 044000;
2.山西大同大学数学与计算机科学学院,山西 大同 037009)
一类Dirichlet边值问题多解的存在性
买阿丽1,卢永红2,孙国伟1
(1.运城学院应用数学系,山西 运城 044000;
2.山西大同大学数学与计算机科学学院,山西 大同 037009)
利用上下解方法结合变分法得到了一类Dirichlet边值问题四解存在的充分条件。关键词:临界点;上下解;多解;Dirichlet边值问题

其中Lu=(p(x)u′)′-q(x)u是Sturm-liouville算子,p,q∈C1[0,1],p,q>0,f(x,u)在[0,1]×R上是连续的且关于u是Lipschitz连续的,对所有的x∈[0,1]。我们可以得到问题(1)的四个解的存在性并给出了解存在的具体范围。
近几年Dirichlet边值问题解的存在性是学者们研究的热点课题[1-7],其主要研究方法包括:临界点理论,不动点理论,拓扑度理论,三临界点理论等方法。
将研究如下的一类Dirichlet边值问题
1 预备知识
设空间H=H′[0,1]是Sobolev空间,定义H的内积如下

由内积导出的范数
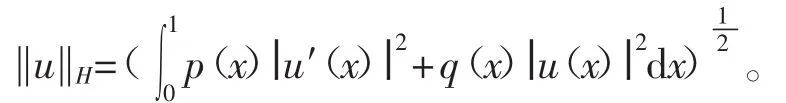
定义空间X=C1[0,1],范数为
‖u‖X=max{maxx∈[0,1]|u(x)|,maxx∈[0,1]|u′(x)|},显然X稠密嵌入H。
定义泛函Φ:H→R如下


由文献[8],问题(1)的解等价于泛函Φ的临界点,即〈Φ′(u),v〉=0,v∈H,其中
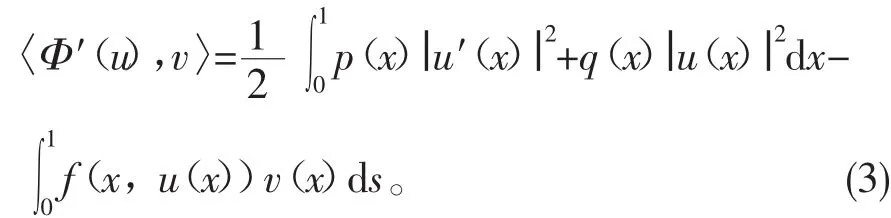
设G(x,s)[9]是以下问题的格林函数

格林函数的性质见文献[1]。
定义1泛函Ø:[0,1]→R是(1)的下解是指如果Ø∈C1[0,1],pØ′∈C1[0,1]使得
-LØ≤f(x,Ø),
Ø(0)≥0,Ø(1)≤0。
定义2泛函ψ:[0,1]→R[0,1]是(1)的上解是指,如果ψ∈C1[0,1],pψ′∈C1[0,1]使得
-Lψ≥f(x,ψ),
ψ(0)≤0,ψ(1)≥0。
2 主要结果
引理1[10]设H是Hibert空间且X是Bancch空间使得X嵌入H。设Φ是定义在H上的C2-0泛函。假设
(1)Φ′(u)=u-Au且Φ′(u)是X到X上的Lips-
(2)K={u∈H:Φ′(u)=0}⊂X。
(3)Φ在H上满足(PS)-条件。
(4)存在X中的两个开凸集D1和D2,D1∩D2≠Ø,A(∂xD1)⊂D1和A(∂xD2)⊂D2。
如果存在一路径h:[0,1]→X使得
h(0)∈D1\D2,h(1)∈D2\D1,
和

其中∂xD和D—X分别是D关于X的边界和闭包。
引理2[1]函数u∈H是泛函Φ的临界点,当且仅当u∈X是方程

引理3 gradΦ(u)=u-Au,其中
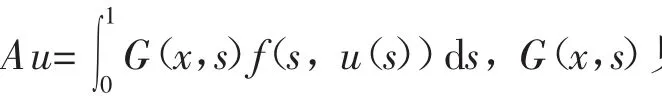
证明对任意的h∈H,。
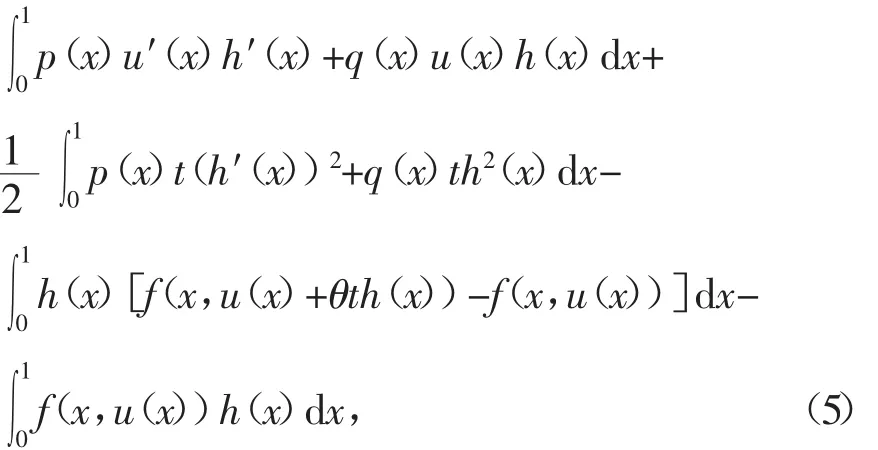
其中0<θ<1。
对任意的h∈H,利用分部积分和格林函数的性质可得,

于是由上式和(5)可得定义线性特征值问题

定义线性特征值问题

(6)有一列特征值(λ1):0<λ1≤λ2≤…≤λj≤…。对应的特征函数是φ1,φ2,…。且‖φ‖iH=1,i=1,2,…,构成H的正交基。
引理4假设(H1)成立,则泛函Φ满足(PS)-条件。
(H1)存在数a,b且λk<a<b<λk+1,k≥2使得
a≤f(′tx,t)≤b,∀x∈[0,1],|t|≥R1。
证明类似于文献[1]中的引理,只需要做如下修改:n

定理1 假设(H1)成立,再假设
(H2)(1)有下解Ø∈C[20,1]和上解ψ∈C[20,1],Ø≤ψ;
(H3)u≤v有(f x,u)≤(f x,v)。
则问题(1)至少四个解。
证明利用引理1证明此定理,下面验证满足引理的条件即可。
设D1={u∈X:u>Ø,x∈[0,1]}和D2={u∈X:u<ψ,x∈[0,1]}。显然D1和D2是X中的开凸集且D1∩D1≠Ø。
若u∈∂xD1且v=Au,则由(H3)得

所以Au≥AØ。
设ω=AØ,下证AØ≥Ø。
事实上,由定义得
-Lω+LØ=-LAØ+LØ≥0,
并由格林函数的性质

同理得ω(1)-Ø(1)≥0。
由引理4,ω≥Ø。故AØ≥Ø。
因此Au≥AØ≥Ø。从而A(∂xD1⊂D1),类似的可证A(∂xD2)⊂D2。
假设(H1)中的k=2,选取路径为


下证Φ(h(rs))→-∞,r→+∞,s∈[0,1]。
注意到(φi,φ)j=0,i≠j,由内积定义易得,

且‖φi‖H=1,i=1,2,…。
因此存在常数C1,C2>0使得

由(H1),存在常数C3,C4>0满足

所以

(6)两边同乘以φ,注意到边界条件,得
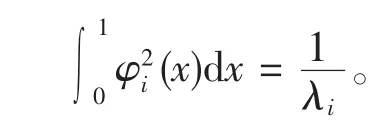
于是(8)变为
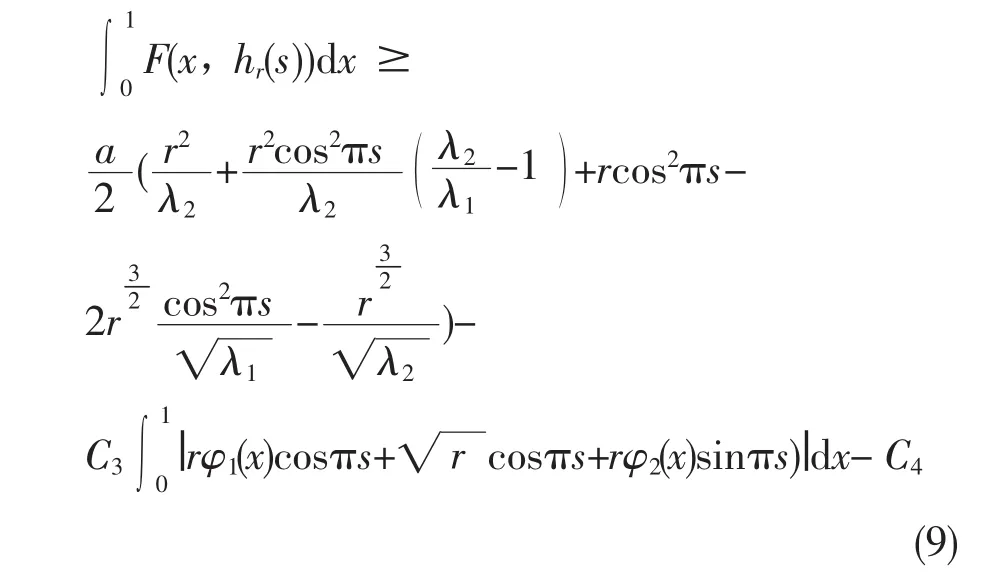
由(7)和(9)得

当r→∞,s∈[0,1]。所以r充分大,

由引理4并应用引理1,问题(1)至少存在四个解,分别为:
[1]Tian Y,Ge W.Multiple solution of Sturm-Liouville boundary value problem via lower an upper solution and variationalmethods [J].Nonliear Anal,2011(74):6733-6744.
[2]BaiZ.Teupperand lowersolutionmethod for some fourth orderboundary valueproblem[J].NonliearAnal,2007,67(15):1704-1709.
[3]Averna D,BonannoG.A tree criticalpoints theorem and itsapplications to theordinary Dirichletproblem[J].TopolMethods Nonliear Anal,2003(22):93-104.
[4]Lin X,Jiang D.Multiple positive solution of Dirichlet boundary value problems for second order impulsive differential equations [J].Jmath Anal Appl,2006(321):,501-514.
[5]Mawhin J,Willem M.Critical Point Theory and Hamiltonian Systems[M].Springer-VerLag:Berlin,1989.
[6]Agarwal R.P,Hong Huei-Lin,Yeh Cheh-Chih.The existence of positive solutions for the Sturm-Liouville boundary value problem[J].ComputMath Appl.1998,35(9):89-96.
[7]卢永红,刘宏英.橄榄树距离和及平均距离的求解[J].山西大同大学学报:自然科学版,2010,26(2):15-17.
[8]Tian Y,GeW.Applications of variationalmethods to boundary value problem for impulsive differential equations[J].Proc.Edinb.Math.Soc,2008(51):509-527.
[9]郭大均,孙经先,刘兆理.非线性常微分方程泛函方法[M].济南:山东科学技术出版社,1995.
[10]Liu Z L,Sun JX.Invariant sets of descending flow in critical point theory with applications to nonlinear differential equations[J].J.Differential Equations,2001(172):257-299.
Multip le S olutions to Dirichlet Boundary Value Problem
MAIA-li1,LU Yong-hong2,SUN Guo-wei1
(1.Department of Applied Mathematics,Yuncheng University,Yuncheng Shanxi,044000;2.School of Mathematics and Computer Science,Datong University,Datong Shanxi,037009)
In this paper,by using lower and upper solutions and variationalmethods,we obtain a sufficient condition of four solutions for a class of Dirichletboundary value peoblem.
c ritical point;l ower and upper solutions;multiple solutions;d irichletboundary value peoblem
1674-0874(2013)01-0006-04
O175.7
A
2012-10-10
运城学院基础研究项目[J C-2009024]
买阿丽(1981-),女,山西河津人,博士,讲师,研究方向:常微分方程及其应用。chitz连续。
〔责任编辑 高 海〕
