生物组织弹性的测量与成像：基于振动的超声检测方法综述

李添捷 郑永平 汪源源

1 复旦大学 (上海 200433)

2 香港理工大学 (香港)

1. 研究背景

生物组织成分与结构的不同很大程度上造成 了其力学特性的差异。例如正常肝脏组织的剪切模量在1KPa的数量级[1,2]。但在炎症反应中，由胶原纤维构成的疤痕组织将取代死亡的肝细胞，随着纤维化进程的发展，胶原纤维将连结肝脏中的管状结构，逐步增加组织硬度，使肝硬化的剪切模量上升到10KPa的数量级。超声技术可以非侵入地检测生物组织对力作用的响应，结合物理模型和信号处理技术，实现生物力学特性的测量和估计。

现实的问题是选用怎样的物理模型，来简化生物组织对力作用的响应。假设施加的激励只在短时间内起作用，即生物组织的力学状态仅取决于现时的负载，那么就可以忽略组织的粘性，而将其视为弹性体[3]。理论上，可以用一个9×9的劲度参数矩阵表征理想的弹性材料，当然测量所有81个参数并不现实。如果进一步将生物组织视为匀质的各项同性材料，那么只需用两个拉梅常数(Lamé Constants)，或由其导出的杨氏模量(Young’s Modulus)和泊松比(Poisson’s ratio)就可以完全表征该生物组织。

目前的超声弹性测量和成像方法大都只专注于组织的弹性，然而实际的测量和成像过程并不像假设的那么理想，生物组织的粘性并非总能忽略[4-6]。理论研究表明，在振动激励源的作用下，生物组织中可以观察到剪切波，随着振动频率的增加，组织的粘性特性逐步体现，表现为剪切波传播速度的增加。Oestreicher等人的研究初略地给出了人体组织的剪切模量和粘度值，分别为2.5KPa和15Pa·s，当振动频率升至25Hz，波速从剪切模量主导转换为粘度主导[7]。Zhang等人探讨了80～220Hz振动激励下牛肝中剪切波的传播，估算的波速为1.5m/s，剪切模量2.2KPa，粘度2Pa·s，振动频率175Hz时，波速从剪切模量主导转换为粘度主导[8]，该数据与Klatt等人利用磁共振弹性成像得到的人体肝脏组织的相关数据吻合[9]。更多研究结果表明，在目前超声弹性成像系统使用的振动频率下，生物组织的劲度参数和粘度都与频率无关，两者均提供了重要的诊断信息[10]。

近二十年来，国际上的一些研究小组深入探讨了生物组织中振动的传播机制，提出了一系列超声检测组织力学特性的方法。这些方法既可以根据激励的时间特性划分为低频连续激励和瞬时激励两类[11]，也可以根据激励的空间特性划分为外部激励源和内部激励源两类[12]。

Parker等人提出的声弹性成像 (Sonoelastography)采用外部振动单元对生物组织施加连续的低频简谐振动，利用多普勒技术得到相应区域组织的振幅和相位信息，考察非正常的生物组织对检测结果的影响[13-15]。Fink等人提出的瞬时弹性成像(Transient Elastography, TE) 则采用外部振动单元在生物组织表面施加一低频脉冲振动，结合互相关运算检测组织的位移，测量横波振动轴向的传播速度[16-20]。

除了外部振动单元，也可采用在生物组织感兴趣区域施加内部激励的方式成像。内部的振动激励可由生物组织自发产生，用于心脏和血管的弹性成像[21,22]，也可借助声辐射力 (Acoustic Radiation Force) 实现[23]。生物组织的共振频率与其力学特性相关，Greenleaf等人提出的振动声成像 (Ultrasound-stimulated Vibro-Acoustic Spectrography, USAE) 采用两束频率相近的超声波束在生物组织内部产生连续的低频振动，继而用水听器观测相关区域的共振现象，成像生物组织的力学特性[24]。在此基础上，Konofagou等人则改用诊断超声探头观测组织共振，结合互相关运算跟踪生物组织在辐射力作用下的位移，提出了谐波运动成像 (Harmonic Motion Imaging,HMI)[25]。内部的振动激励也可以是瞬时脉冲信号，Nightingale等人提出的辐射力脉冲成像 (Acoustic Radiation Force Impulse, ARFI) 既可以测量组织内部横波振动的传播速度，也可以得到生物组织中剪切模量的分布[26-29]。与之类似，Fink等人运用声辐射力激励生物组织特定区域，使激励源以超音速移动从而形成平面波波阵面，结合互相关运算检测组织位移，跟踪音爆现象(Sonic Boom)中马赫锥(Mach Cone)的传播，得到组织剪切模量，这种方法称为超音速剪切成像 (Supersonic Shear Imaging, SSI)[30,31]。

本文的主要目的是对现阶段各种基于振动激励源的超声测量和成像方法进行综述。在接下来的部分中，将首先介绍相关的物理基础，诠释不同方法的内在联系，并在此基础上，介绍各种典型方法的实现原理和技术关键，最后探讨现阶段研究中的不足，对该领域未来的研究方向进行展望。

2. 物理基础

物理学研究的成果为组织弹性超声检测方法的设计提供了理论依据，具有非常重要的指导意义。本节将抛开这些方法研究中繁杂的设计过程和技术细节，着重揭示不同方法背后共同的物理本质。

2.1 生物组织力学特性的表征

如果将生物组织视为各向同性的匀质弹性体，则可用两个拉梅常数，或其导出的杨氏模量和泊松比完全表征其力学特性。一阶拉梅常数λ表示组织的压缩性，二阶拉梅常数µ表示组织的剪切模量。拉梅常数与杨氏模量E和泊松比υ的转换关系为[32]：

通常认为生物组织不可压缩，将υ近似为0.5[10,14]，可由式(2)得E与µ的简化关系：

现有的基于振动的超声弹性测量和成像技术，归根到底是探知生物组织的力学参数µ或E。通常可以借助组织应变的测量，结合力学参数与应变的关系加以实现。

2.2 力作用下的组织应变

力作用下均匀介质中质点的位移矢量方程既可以描述准静态力作用下的组织应变，也可以描述激励源为振动时的组织应变，是各种弹性测量和成像方法共同的物理基础。

理论上，若忽略体力(如重力)的影响，位移矢量方程表述为如下形式[33]：

其中ρ为质点处的介质密度，u表示质点位移。结合生物组织模型和振动激励的形式，可以确定方程的边界和初始条件，进而求解生物组织对力作用的响应。准静态情况下，施加的外力缓慢作用于生物组织，应变的测量总是在质点运动停止之后，因此ü为零；若将振动施加到生物组织，应变始终会随时间变化，因此ü不为零。

进一步假设生物组织不可压缩，则有 。准静态力作用下方程(4)简化为：

仅考虑轴向的应力和应变，方程的解对应于应变(位移的导数)为常数的情况，这就构成了传统准静态压缩弹性成像(Elastography)[34-36]的物理基础。

当激励源为振动时，方程(4)右侧不为零，情况会复杂一些。方程左侧第一项为压缩波(Compressional Waves)对质点位移的贡献，第二项为剪切波(Shear Waves)的贡献。根据生物组织不可压缩的假设，第一项为零，压缩波的作用被忽略，方程化简为：

2.3 剪切波与压缩波

图1. 生物组织中机械波的传播形式 (a) 生物组织中的振动激励源；(b) 压缩波的传播；(c) 横向传播的剪切波；(d) 轴向传播的剪切波

剪切波和压缩波是生物组织中重要的机械波传播形式。前者仅与组织的剪切模量有关，反映了不改变传播媒介密度的剪切运动；后者与两个拉梅常数都有关，反映了传播过程中引起传播密度变化的运动。图1显示了振动激励下生物组织中机械波的三种传播形式，分别是压缩波、横向传播的剪切波和纵向传播的剪切波。

压缩波沿质点振动方向传播，改变了媒介密度。横向剪切波不改变组织密度，但会使媒介中质点发生旋转，传播方向与振动方向垂直。剪切波还可以像压缩波一样沿轴向传播，此时质点并不发生旋转，由于组织的不可压缩性，媒介沿振动方向的压缩和伸展将同时造成其横向的伸展和压缩，从而形成轴向剪切波。值得注意的是横向和轴向的剪切波具有相同的传播速度，两者往往同时存在，将组织中的振动传播开去[10]。

进一步讨论压缩波和剪切波的传播速度，首先考虑压缩波引起的位移。已知矢量恒等式，压缩波情况下有 ，因此可以将式(4)简化为：

其中压缩波波速cp为：

继而考虑剪切波引起的位移。由于轴向和横向传播的剪切波均不改变媒介密度，因此 ，式(4)简化为：

其中剪切波波速cs表示为：

中国是世界上崩塌灾害最为严重的地区之一[1]，特别是自20世纪80年代以来，随着我国工程建设的高速发展，崩塌灾害在我国呈逐年加重趋势。崩塌在我国的各个区域基本上均有分布，但主要集中分布在地形变化大、地质构造作用强烈的地区，尤其是以环青藏高原第一阶梯的四川、云南、贵州、重庆、甘肃、青海等省最为严重，给人民群众的生命财产造成了极大损失，严重影响铁路、公路、水电站等基础设施的安全。

生物组织中压缩波波速大于剪切波波速若干数量级，可在弹性测量和成像中忽略其对组织位移的影响，即可假设组织中仅存在不改变媒介密度的剪切波，因而有 。这与生物组织不可压缩的假设是一致的。此外，式(10)所示的波速公式表明生物组织的剪切模量决定了其中剪切波的传播速度，构成了基于剪切波波速的弹性测量和成像方法的物理基础。

2.4 声辐射力

生物组织中的剪切波只能在距离波源几个波长的有限区域中传播，基于剪切波的弹性成像技术只能测量振动激励附近组织的弹性参数[10]。由于超声波会在其传播路径上对媒介产生辐射力，因而利用该现象可以将振动激励施加到生物组织内部感兴趣区域，扩大超声弹性和成像方法的应用范围，在振动声成像USAE[24]、谐波运动成像HMI[25]、辐射力脉冲成像 ARFI[26-28]和超音速剪切成像 SSI[30]中得到了广泛的应用。

当超声垂直入射到具有吸收和散射特性的目标介质时，辐射力的方向与传播路径一致，大小由下式给出[23]：

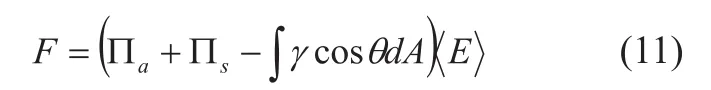
其中Πa和Πs分别为目标介质的吸收和散射功率，γ和θ分别为散射强度和散射角，dA为目标介质轴面上投影的面积微元，〈E〉为平均声能量密度。

生物组织可以假设为众多直径远小于一个波长的瑞利散射子(Rayleigh Scatterer)的集合，声波传播产生的总辐射力等于其在每一散射子上辐射力的总和。对于单一的瑞利散射子，入射声波将均匀地向四面八方散射，式(11)中的积分项为0，辐射力化简为：

生物组织中吸收作用主导声波的衰减，可以进一步忽略散射项，将总辐射力简化为：

理论研究表明平面波条件下生物组织中的辐射力可以表述为[23,28]：

其中声辐射力F是一种体力，c为介质中的声速，α为组织的吸收系数，I为声强，也可以称为平均声能量流密度。

3. 典型方法

基于振动可实现生物组织力学参数的测量和成像，其本质在于应变的检测，并构建其与生物组织力学参数的关系。在一系列典型的成像方法中，振动源可以是连续的，也可以是瞬时的；激励可以由外部振动单元产生，也可以利用声辐射力施加到内部感兴趣区域。本节将具体介绍目前流行的六种超声弹性成像技术的实现原理。

3.1 声弹性成像 (Sonoelasticity)

Parker等人提出的声弹性成像采用外部振动单元，在生物组织表面施加连续的低频简谐振动，利用多普勒技术，得到相关区域组织的振幅信息[13-15]。Sato等人则采用了类似的实验装置，提出了基于相位的声弹性成像[39]。

假设被测的健康组织具有均一的剪切模量µ，相关区域将以本征模式(Eigenmode)响应外部的振动激励，表现为振动幅度一致，相位变化均匀。非正常组织的出现使得方程(6)中µ随位置改变，引起组织应变幅度和相位的改变[13]。

假设介质中散射子的振幅ξ0、角频率ωb、相位φb，振动方程表示为：

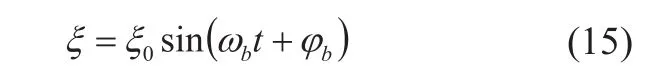
结合多普勒频偏公式，可以得到超声回波信号：

其中s0为回波信号幅度，φ为传播造成的相移，调制指数mf与多普勒现象相关，定义为：

其中c为超声波声速，生物组织中通常为1540m/s。采用正交解调电路可得到与组织运动相关的两个多普勒信号：

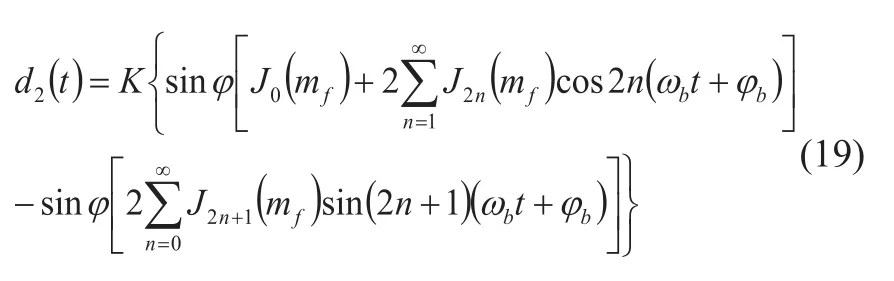
其中Ji(x)为第i阶贝塞尔函数(Bessel Function)。从中可以看出解调后的多普勒超声信号具有直流分量和倍频频谱，分析d1(t)和d2(t)的频谱，可查阅贝塞尔函数表确定mf，进而得到所求的散射子振幅ξ0；也可分析d1(t)或d2(t)的基波分量得到相位φb。

3.2 瞬时弹性成像TE

Fink等人提出的瞬时弹性成像则采用外部振动单元在生物组织表面施加低频脉冲振动，通过跟踪剪切波的传播速度评估生物组织的弹性[16]。

图2为瞬时弹性成像早期的结构原理图。实验采用透射(Transmission)模式检测剪切波的传播，即将激励与检测单元放置于仿体对侧，因此接收到的回波实际上是超声探头与振动单元连线上组织随时间变化的RF信号。对该信号作互相关分析，即得到不同深度组织随时间变化的应变图。随着时间的推移，仿体的应变从振动源位置起沿轴线传播到超声探头后，又反射回去。通过测量应变传播的斜率，即可估算出反应剪切模量的剪切波传播速度。

图2. 瞬时弹性成像的结构原理图

透射模式在临床的应用中存在困难，之后提出的反射(Reflection)模式的瞬时弹性成像很好地解决了这个问题[20]。该方法将振动单元集成到超声探头上，但需要选择合适的参考平面，用以补偿探头振动带来的应变测量的误差。

与瞬时弹性成像相关的另一技术上的变形是Zheng等人提出的测量剪切波横向传播速度的方法[40]。该方法在振源附近一定横向距离的位置设置两条超声观察线，通过检测剪切波经过时的时间差异，估计剪切波波速，可用于肌肉弹性的研究[41]。此外，该研究小组的研究表明结合B型超声图像引导，可以提高瞬时弹性成像测量的精度，在肝组织纤维化的评估中有重要的临床应用价值[42,43]。

3.3 振动声成像USAE和组织谐波运动成像HMI

声辐射力的运用丰富了生物组织超声弹性测量和成像的研究。Greenleaf等人提出的振动声成像将连续低频振动施加到组织内部感兴趣区域，并采用水听器观测相关区域的共振[24]，图3为USAE系统的结构原理图。根据式(14)，声辐射力的大小正比于声强I。该方法利用这一关系，将两束频率相近的超声信号聚焦到生物组织感兴趣区域。拍现象使得聚焦区域的声强随时间周期性变化，因而辐射力也做相应的周期变化，聚焦处的生物组织以差频∆f振动。由于生物组织的力学特性决定了共振频率，共振频率的不同又会造成组织响应振动幅度和相位的差异，因此可以用水听器探测这些差异，借以表征力学特性。

USAE系统的结构使其在临床的应用中存在困难，针对这一缺点，Konofagou等人改用诊断超声探头观测组织共振，将振动的激励和检测单元置于待检生物组织的一侧，提出了谐波运动成像HMI。图4为HMI系统的结构原理图[25]。该方法同样采用拍现象在组织内施加连续的低频振动，区别在于采用了超声探头检测组织的共振响应。运用互相关运算分析采集到的RF信号，便可以得到检测线上生物组织随时间的应变图。

3.4 声辐射力脉冲成像ARFI

图3. 振动声成像的结构原理图

除了连续低频振动的方式，声辐射力也可短暂地作用于生物组织内部，其中一个经典的方法是Nightingale等人提出的辐射力脉冲成像ARFI[26-28]。事实上，该方法并不仅限于采用振动激励源来成像，也可在特定的感兴趣区域生成准静态的力作用，得到组织的应变分布[28]。本文讨论的重点是振动激励源条件下生物组织弹性的测量与成像。

当采用该方法检测波速时，需要首先选择一个感兴趣的测量区域；然后将可聚焦的超声探头转为激励模式，在测量区域附近施加一个短暂的振动；再将探头转为检测模式扫描测量区域，结合互相关分析即可得到应变图像，并由振动传播到测量区域的时间推算剪切波波速。式(6)表明由组织的位移可以计算剪切模量。根据这一关系，该研究小组进一步实现了剪切模量的二维成像[26]。事实上，无论是剪切波波速的测量，还是剪切模量成像的实现，关键都在于激励序列和检测序列的设计，以及组织应变的估计。

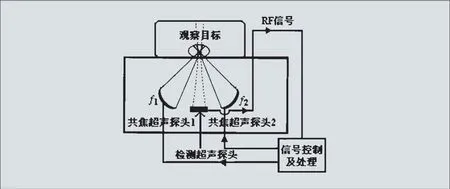
图4. 组织谐波运动成像原理图

3.5 超音剪切成像SSI

质点在超音速振动时会产生音爆，Fink等人提出的超音剪切成像SSI利用声辐射力激励特定区域，使对应生物组织内的激励源以超音速移动以形成一个简单的波阵面，结合高帧率(5000帧/s[19])二维超声成像系统，跟踪马赫锥的传播，估计剪切模量。

图5. 超音剪切成像原理图

图5为SSI系统的实现原理。与二维的ARFI系统类似，该方法采用了可聚焦的超声探头激励组织产生振动，继而检测组织对振动的响应。整个成像过程中超声探头在激励模式和检测模式间转换，区别在于该方法采用了不同的二维应变估计和剪切波波速测量方法。前者包括波束成形(Beamforming)、二维斑点跟踪(Speckle Tracking)、以及剪切模量估计三个关键步骤，后者则通过跟踪二维应变图中马赫锥的传播实现。

图5中的数据处理部分描述了二维应变图的计算流程。在每一检测时刻，超声探头从两个不同角度采集到左右两组RF回波信号。假设检测时超声信号垂直发射到生物组织，两组回波信号的接收角度关于发射信号对称，分别为α0和α1，且有α0=-α1。分别对前后时刻两组数据进行互相关分析，可以得到两组同一时刻组织运动引起的回波信号的时间偏移tα0和tα1，由式 (20)和 (21)计算x和z方向上生物组织的应变，即可生成二维应变图[37]。

在二维应变图的基础上可估计剪切模量µ。SSI法仅考虑了组织在xz平面中的应变，因而剪切模量µ的频域表达式为[30]：

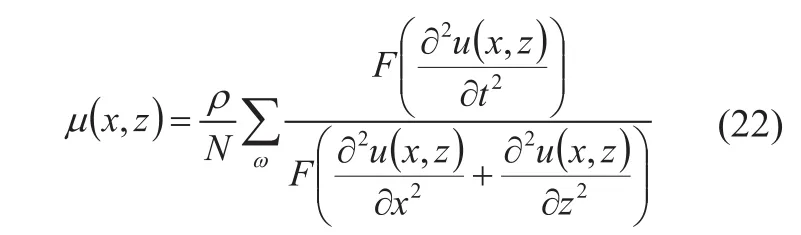
其中F表示傅里叶变换，N则为估计中频谱线的个数。

4. 展望未来

生物组织力学特性的超声测量和成像是医学超声学研究的前沿课题。近二十年来，一些研究小组在该领域进行了广泛的研究，提出许多别具特色的方法。本文介绍了不同超声弹性测量和成像方法背后的物理本质，并对现阶段各种基于振动激励源的方法进行了综述。这些方法在一定程度上量化了组织的力学特性，与传统的超声成像技术相互补充，在生物医学的科学研究和临床应用中具有广泛前景。尤其是基于声辐射力和剪切波的声辐射力脉冲成像ARFI和超音剪切成像SSI，由于其检测过程无需操作者对目标组织施加力作用，可重复性高；测量结果受组织整体状态影响较小，局域性好，值得关注。

然而这些方法从提出到实际应用，仍有很多理论和实际的问题需要解决。例如，ARFI在肝纤维化评估[44,45]和肿瘤良恶性鉴别[46,47]中具有重要的应用价值，但在脾脏和移植肾等人体组织的应用中，多次测量的结果缺乏一致性[48]。其原因可能在于现有的研究忽略了生物组织结构参数的复杂性，未考虑超声传播过程中的衰减，夸大了聚焦区域的力作用。另一方面，人体的呼吸运动、胃肠蠕动以及血液循环都会对被测组织造成额外的力作用，影响组织力学特性的测量。因此，如何在成像中完善辐射力的估计，探讨人体运动对生物组织力学特性测量的影响，可能是今后弹性测量和成像技术研究的重要方向。

此外，生物组织的病理状态可以表现为多种力学参数的改变，目前的弹性测量和成像技术大都忽视了生物组织的粘性，仅用剪切模量评估组织的力学特性。有学者探讨了ARFI中组织的位移峰值、到达峰值的时间、恢复时间和组织密度与杨氏模量的关系[49]，但未涉及这些参数的成像，及其在疾病甄别中的价值。因此，如何进一步研究生物组织的力学特性参数，量化这些参数在疾病甄别中的价值，对弹性测量和成像技术的发展和应用至关重要。

致谢：

感谢国家自然科学基金(11228411)和香港理工大学基金(G-U803)对本研究的资助。

[1]Catheline S, Gennisson JL, Fink M. Measurement of elastic nonlinearity of soft solid with transient elastography. The Journal of the Acoustical Society of America, 114(6): 3087-3091, 2003.

[2]Abraham Cohn N, Kim BS, Erkamp RQ, Mooney DJ, Emelianov SY, Skovoroda AR, O'Donnell M. High-resolution elasticity imaging for tissue engineering. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 47(4): 956-966, 2000.

[3]Ophir J, Alam SK, Garra B, Kallel F, Konofagou E, Krouskop T, Varghese T. Elastography: ultrasonic estimation and imaging of the elastic properties of tissues. Proceedings of the Institution of Mechanical Engineers, 1999. vol. 213, part H, pp. 203-233.

[4]Catheline S, Gennisson JL, Delon G, Fink M, Sinkus R, Abouelkaram S, Culioli J. Measurement of viscoelastic properties of homogeneous soft solid using transient elastography: an inverse problem approach. The Journal of the Acoustical Society of America, 116(6): 3734-3741, 2004.

[5]Bercoff J, Tanter M, Muller M, Fink M. The role of viscosity in the impulse diffraction f i eld of elastic waves induced by the acoustic radiation force. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 51(11): 1523-1536, 2004.

[6]Deff i eux T, Montaldo G, Tanter M, Fink M. Shear wave spectroscopy for in vivo quantif i cation of human soft tissues viscoelasticity. IEEE Transactions on Medical Imaging, 28(3): 313-322, 2009.

[7]Oestreicher HL. Field and impedance of an oscillating sphere in a viscoelastic medium with an application to biophysics. The Journal of the Acoustical Society of America, 23(6): 707-714, 1951.

[8]Zhang M, Castaneda B, Wu Z, Nigwekar P, Joseph JV, Rubens DJ, Parker KJ. Congruence of imaging estimators and mechanical measurements of viscoelastic properties of soft tissues. Ultrasound in Medicine and Biology, 33(10): 1617-1631, 2007.

[9]Klatt D, Asbach P, Rump J, Papazoglou S, Somasundaram R, Modrow J, Braun J, Sack I. In vivo determination of hepatic stiffness using steady-state free precession magnetic resonance elastography. Investigative Radiology, 41(12): 841-848, 2006.

[10]Carstensen EL, Parker KJ, Lerner RM. Elastography in the management of liver disease. Ultrasound in Medicine and Biology,34(10): 1535-46, 2008.

[11]Taylor LS, Porter BC, Rubens DJ, Parker KJ. Three-dimensional sonoelastography: principles and practices. Physics in Medicine and Biology, 45(6): 1477-1494, 2000.

[12]Greenleaf JF, Fatemi M, Insana M. Selected methods for imaging elastic properties of biological tissues. Annual Review of Biomedical Engineering, 5: 57-78, 2003.

[13]Gao L, Parker K, Alam S, Lerner R. Sonoelasticity imaging: theory and experimental verif i cation. Journal of The Acoustical Society of America, 97(6): 3875-3886, 1995.

[14]Parker K, Huang S, Musulin R, Lerner R. Tissue response to mechanical vibrations for "sonoelasticity imaging". Ultrasound in Medicine and Biology, 16(3): 241-246, 1990.

[15]Lerner RM, Huang S, Parker KJ. “Sonoelasticity” images derived from ultrasound signals in mechanically vibrated tissues.Ultrasound in Medicine and Biology, 16(3): 231-239, 1990.

[16]Catheline S, Wu F, Fink M. A solution to diffraction biases in sonoelasticity: the acoustic impulse technique. Journal of the Acoustical Society of America, 105(5): 2941-2950, 1999.

[17]Montaldo G, Tanter M, Bercoff J, Benech N, Fink M. Coherent plane-wave compounding for very high frame rate ultrasonography and transient elastography. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 56(3):489-506, 2009.

[18]Bercoff J, Chaffai S, Tanter M, Sandrin L, Catheline S, Fink M, Gennisson JL, Meunier M. In vivo breast tumor detection using transient elastography. Ultrasound in Medicine and Biology, 29(10): 1387-1396, 2003.

[19]Sandrin L, Tanter M, Catheline S, Fink M. Shear modulus imaging with 2-D transient elastography. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 49(4): 426-435, 2002.

[20]Sandrin L, Tanter M, Gennisson JL, Catheline S, Fink M. Shear elasticity probe for soft tissues with 1-D transient elastography.Ultrasonics, Ferroelectrics and Frequency Control, IEEE Transactions on, 49(4): 436-446, 2002.

[21]Konofagou EE, D'Hooge J, Ophir J. Myocardial elastography: a feasibility study in vivo. Ultrasound in Medicine and Biology,28(4): 475-482, 2002.

[22]Mai JJ, Insana MF. Strain imaging of internal deformation. Ultrasound in Medicine and Biology, 28(11): 1475-1484, 2002.

[23]Torr G. The acoustic radiation force. American Journal of Physics, 52(5): 402-408, 1984.

[24]Fatemi M, Greenleaf JF. Ultrasound-stimulated vibro-acoustic spectrography. Science, 280(5360): 82-85, 1998.

[25]Konofagou EE, Hynynen K. Localized harmonic motion imaging: theory, simulations and experiments. Ultrasound in Medicine and Biology, 29(10): 1405-1413, 2003.

[26]Nightingale K, McAleavey S, Trahey G. Shear-wave generation using acoustic radiation force: In vivo and ex vivo results.Ultrasound In Medicine and Biology, 29(12): 1715-1723, 2003.

[27]Nightingale K, Soo MS, Nightingale R, Trahey G. Acoustic radiation force impulse imaging: in vivo demonstration of clinical feasibility. Ultrasound in Medicine and Biology, 28(2): 227-235, 2002.

[28]Nightingale KR, Palmeri ML, Nightingale RW, Trahey GE. On the feasibility of remote palpation using acoustic radiation force.Journal of the Acoustical Society of America, 110(1): 625-634, 2001.

[29]Palmeri ML, McAleavey SA, Trahey GE, Nightingale KR. Ultrasonic tracking of acoustic radiation force-induced displacements in homogeneous media. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 53(7): 1300-1313, 2006.

[30]Bercoff J, Tanter M, Fink M. Supersonic shear imaging: a new technique for soft tissue elasticity mapping. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 51(4): 396-409, 2004.

[31]Bercoff J, Tanter M, Fink M. Sonic boom in soft materials: the elastic Cerenkov effect. Applied Physics Letters, 84(12): 2202-2204, 2004.

[32]徐芝纶. 弹性力学(上册) (第4版 Edition). 高等教育出版社, 北京, 2006.

[33]Parker KJ, Doyley MM, Rubens DJ. Imaging the elastic properties of tissue: the 20 year perspective. Physics in Medicine and Biology, 56(2): 513-513, 2011.

[34]Garra BS, Cespedes EI, Ophir J, Spratt SR, Zuurbier RA, Magnant CM, Pennanen MF. Elastography of breast lesions: initial clinical results. Radiology, 202(1): 79-86, 1997.

[35]Cespedes I, Ophir J, Ponnekanti H, Maklad N. elastography: elasticity imaging using ultrasound with application to muscle and breast in-vivo. Ultrasonic Imaging, 15(2): 73-88, 1993.

[36]Ophir J, Cespedes I, Ponnekanti H, Yazdi Y, Li X. Elastography: a quantitative method for imaging the elasticity of biological tissues. Ultrasonic Imaging, 13(2): 111-134, 1991.

[37]Tanter M, Bercoff J, Sandrin L, Fink M. Ultrafast compound imaging for 2-D motion vector estimation: application to transient elastography. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 49(10): 1363-1374, 2002.

[38]Catheline S, Thomas JL, Wu F, Fink MA. Diffraction field of a low frequency vibrator in soft tissues using transient elastography. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 46(4): 1013-1019, 1999.

[39]Yamakoshi Y, Sato J, Sato T. Ultrasonic imaging of internal vibration of soft tissue under forced vibration. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 37(2): 45-53, 1990.

[40]Wang CZ, Guo JY, Zheng YP. Muscle elasticity measurement using ultrasound at isometric step contraction. World Congress of Biomechanics, Singapore, 2010. IFMBE Proceedings, 31:965-968.

[41]Wang CZ, Zheng YP. Development of a vibro-ultrasound method for skeletal muscle stiffness assessment under high-levels of isometric contraction. International Tissue Elasticity Conference (ITEC), Arlington, Texas, USA, Oct 12-15, 2011. ITEC Proceedings, p95.

[42]Zheng YP, Mak TM, Huang ZM, Cheung CWJ, Zhou YJ, He JF. Liver f i brosis assessment using transient elastography guided with real-time B-mode ultrasound imaging. World Congress of Biomechanics, Singapore, 2010. IFMBE Proceedings, 31:1036-1039.

[43]郑永平, 麦德民, 黄铮铭, 张忠伟, 周永进, 何俊峰. 实时B超引导下的瞬时弹性肝纤维化评估. 中国医疗设备, 26(1):34-37, 2011.

[44]Takahashi H, Ono N, Eguchi Y, Eguchi T, Kitajima Y, Kawaguchi Y, Nakashita S, Ozaki I, Mizuta T, Toda S, Kudo S, Miyoshi A, Miyazaki K, Fujimoto K. Evaluation of acoustic radiation force impulse elastography for f i brosis staging of chronic liver disease: a pilot study. Liver International, 30(4): 538-545, 2010.

[45]Bavu E, Gennisson JL, Couade M, Bercoff J, Mallet V, Fink M, Badel A, Vallet-Pichard A, Nalpas B, Tanter M, Pol S.Noninvasive in vivo liver f i brosis evaluation using supersonic shear imaging: a clinical study on 113 Hepatitis C virus patients.Ultrasound in Medicine and Biology, 37(9): 1361-1373, 2011.

[46]Friedrich-Rust M, Romenski O, Meyer G, Dauth N, Holzer K, Grünwald F, Kriener S, Herrmann E, Zeuzem S, Bojunga J.Acoustic radiation force impulse-imaging for the evaluation of the thyroid gland: a limited patient feasibility study. Ultrasonics,52(1): 69-74, 2012.

[47]Athanasiou A, Tardivon A, Tanter M, Sigal-Zafrani B, Bercoff J, Eux TD, Gennisson JL, Fink M, Neuenschwander S. Breast lesions: quantitative elastography with supersonic shear imaging-preliminary results. Radiology, 256(1): 297-303, 2010.

[48]Goertz RS, Amann K, Heide R, Bernatik T, Neurath MF, Strobel D. An abdominal and thyroid status with acoustic radiation force impulse elastometry-a feasibility study acoustic radiation force impulse elastometry of human organs. European Journal of Radiology, 80(3): E226-E230, 2011.

[49]Palmeri ML, McAleavey SA, Fong KL, Trahey GE, Nightingale KR. Dynamic mechanical response of elastic spherical inclusions to impulsive acoustic radiation force excitation. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 53(11): 2065-2079, 2006.