CRTS-Ⅱ型板式无砟轨道线路路基不均匀沉降限值研究

徐庆元，范浩，李斌，周小林

(中南大学 土木工程学院，湖南 长沙，410075)

路基不均匀沉降限值是高速铁路路基上板式无砟轨道线路的关键技术参数，对列车-板式无砟轨道-路基系统振动特性、板式无砟轨道各部件动应力特性、疲劳破坏特性及高速铁路造价都有很大影响。若路基不均匀沉降限值标准过高，则将大大增加高速铁路造价，若路基不均匀沉降限值技术标准过低，则不但列车高速运行时旅客的舒适性会受到很大影响，甚至会严重威胁到列车运行的安全。路基上板式无砟轨道线路路基不均匀沉降限值合理值是工程界十分关注的问题。目前，国内外对路基不均匀沉降荷载对路基上CRTS-Ⅱ型板式无砟轨道力学特性影响进行了相关研究，但大多将列车荷载取为一固定的无砟轨道设计动荷载，从静力角度[1-2]进行研究。实际上，列车荷载是随着无砟轨道线路路基不均匀沉降变化而变化的，其大小需要运用列车—无砟轨道—路基耦合动力学原理进行分析研究，统一用固定的无砟轨道设计动荷载对路基不均匀沉降下无砟轨道力学特性进行研究是不合理的。另外，无砟轨道各部件动力系数(如扣件压力和扣件拉力)并不是一个常数，静力计算不能很好地反映这一情况，与实际情况有较大差别。为此，本文作者在国内外列车－路基上无砟轨道耦合动力学理论[3-8]基础上，考虑无砟轨道各部件间及无砟轨道与路基间接触状态非线性，考虑CRTS-Ⅱ型板开裂的影响，建立列车-路基上 CRTS-Ⅱ型板式无砟轨道三维非线性有限元耦合动力学模型，在自重荷载、轨道中长波随机不平顺、轨道短波随机不平顺、路基不均匀沉降荷载、无砟轨道板温度梯度荷载共同作用下，对列车-路基上CRTS-Ⅱ型板式无砟轨道系统耦合振动特性进行研究。在此基础上，提出同时考虑旅客的舒适性和无砟轨道各部件承载力的路基上CRTS-Ⅱ型板式无砟轨道线路路基不均匀沉降限值合理取值。

1 耦合动力学模型

1.1 动车组

将动车组的动车和拖车均视为车体、转向架和轮对组成的多刚体系统，车体和转向架有沉浮、横移、侧滚、点头、摇头共5个自由度，轮对有沉浮、横移、侧滚、摇头4个自由度，有1节动车或拖车，模型共有31个自由度[9]，则高速动车组有31m个自由度(其中，m为动车组编组数)。

1.2 无砟轨道及路基

无砟轨道三维实体单元模型[8]能较好地反映无砟轨道复杂空间力学特性，对作用在无砟轨道上的各种荷载都能模拟。本文亦采用三维实体单元模型作为无砟轨道动力分析模型。

图1所示为路基上CRTS-Ⅱ型板式无砟轨道动力学模型。模型中，钢轨用空间梁单元模拟，轨道板、

底座以实体单元模拟，钢轨与轨道板之间的连接用弹簧单元模拟，轨道板与底座间连接、底座下路基用接触单元模拟。可以考虑在自重荷载、路基不均匀沉降荷载、无砟轨道板温度梯度荷载和列车荷载共同作用下，无砟轨道板和CA砂浆、底座和路基间可能脱空对无砟轨道动力特性的影响。

图1 路基上CRTS-Ⅱ型板式无砟轨道动力学模型Fig. 1 Dynamic mechanical model of CRTS II-type slab track on subgrade

路基上CRTS-Ⅱ型板式无砟轨道轨道板内钢筋在纵向是连续的，但混凝土是按开裂设计的。为了考虑无砟轨道混凝土开裂对列车-路基上 CRTS-Ⅱ板式无砟轨道耦合系统动力特性的影响，轨道板之间、底座之间设置纵向连接单元，纵向连接单元刚度取为无砟轨道混凝土开裂后裂缝处的刚度。

根据连续配筋无砟轨道结构的研究成果[1]，连续配筋无砟轨道结构裂缝间距不能过大，否则，裂缝宽度会过大，进而影响到无砟轨道结构的耐久性；裂缝间距也不能过小，否则，无砟轨道结构受力较不利。合理的裂缝间距为1.0～2.5 m，相当于2～4个扣件间距。由于以上原因，本文模拟连续配筋的路基上CRTS-Ⅱ型板式无砟轨道结构时，裂缝间距考虑2种工况，分别是2个扣件间距(1.3 m)和4个扣件间距(2.6 m)。

扣件尺寸对无砟轨道应力，特别是轨道板(道床板)横向应力有一定的影响。为了考虑扣件的尺寸效应，将每个钢轨节点与其对应扣件尺寸范围内的轨道板节点相连。

1.3 轮轨关系

轮轨垂向作用力由著名的赫兹非线性弹簧接触理论[9]确定：

式中：G为轮轨接触常数，m/N2/3；Zw(j，t)为t时刻第j位车轮的垂向位移，m；Zr(j，t)为t时刻第j位车轮下钢轨的垂向位移，m；Z0(t)为轮轨界面存在的垂向不平顺。

采用文献[10]中的横向轮轨关系模型模拟轮轨之间的横向作用力：

式中：KY为车辆重力刚度，为车辆轴重和轮轨间等效锥度之积；Yw(j，t) 为t时刻第j位车轮的横向位移, m；Yr(j，t)为t时刻第j位车轮下钢轨的横向位移, m；Y0(t)为轮轨界面存在的横向不平顺；CY与轮轨间蠕滑有关,其值为f22/v(其中，f22为轮轨间横向蠕滑系数，v为列车速度)。

1.4 荷载

1.4.1 中长波随机不平顺

由于我国还缺乏高速铁路无砟轨道谱，本文采用德国适用于时速 250 km/h以上的高速铁路低干扰功率谱密度对中长波(波长为1～80 m)随机不平顺进行模拟[9]。

不同样本的随机不平顺计算结果差别较大，而工程结构物的设计通常需要一定的安全富裕，为此，本文先采用较粗的网格尺寸，对50组不同样本随机不平顺下耦合系统进行动力分析，找出使耦合系统动力响应最大的随机不平顺样本，以此作为中长波随机不平顺样本供研究分析。

1.4.2 短波随机不平顺

无砟轨道线路上除了中长波随机不平顺外，还存在由于轮轨间不均匀磨耗等原因形成的对轮轨高频振动及噪声辐射有很大影响的短波随机不平顺。

Sato谱[11]是目前国内外进行轮轨高频振动及噪声辐射研究时广泛采用的谱模型，Sato谱的谱密度表达式为S(Ω)=A/Ω3(式中：Ω为空间频率；A为粗糙度常数，为 4.15×10-8～5.00×10-7m·rad)。

西南交通大学结合秦沈客运专线无砟轨道实测数据对 Sato谱进行了研究[12]，建议A取为 3.15×10-7m·rad，本文采用西南交通大学的研究成果进行短波随机不平顺模拟。

1.4.3 路基不均匀沉降荷载

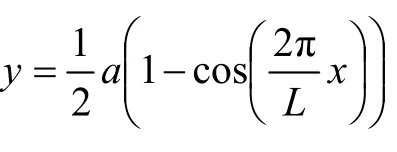
1.4.4 无砟轨道温度梯度荷载

根据文献[1]，无砟轨道板正温度梯度取为 95℃/m，负温度梯度取为 48 ℃/m，并考虑板厚修正系数，0.20 m厚板修正值为1.05。

1.4.5 自重荷载

由于自重荷载在无砟轨道各部件间形成的初始应力对无砟轨道各部件间及无砟轨道与路基间接触状态非线性有较大影响[2]，因此，在列车、无砟轨道各部件施加自重荷载，以反映自重荷载对耦合系统动力特性的影响。

1.5 耦合动力学系统初始条件

在列车、无砟轨道各部件施加自重荷载，在无砟轨道板上施加温度梯度荷载，在路基底面施加路基不均匀沉降荷载，在这些荷载作用下对列车-路基上板式无砟轨道系统静力进行计算，其结果作为动力分析的初始条件。

1.6 耦合动力学模型求解

由于采用实体单元模拟无砟轨道板，本文列车-路基上板式无砟轨道耦合动力学模型自由度较多(超过10万个)，耦合系统振动方程的快速求解十分重要。与大型稀疏矩阵的直接求解算法相比，预处理共轭梯度法(PCG法)具有一定的优势[13]。本文采用PCG法进行大型稀疏矩阵的快速求解，可以在普通微机上对列车-路基上板式无砟轨道耦合系统进行动力仿真研究。

2 路基不均匀沉降限值评价指标

分析中路基不均匀沉降限值评价指标包括以下几个。

(1) 车体垂向振动加速度容许值取为0.13g(1g=9.8 m/s2)。

(2) 最大轮轨垂向力容许值取为高速客运专线设计动荷载设计值300 kN。

(3) 钢轨最大应力容许值取为350 MPa。

(4) 扣件最大拉力(扣压力损失)容许值取为12 kN。

(5) CA砂浆压应力容许值取为3 MPa。

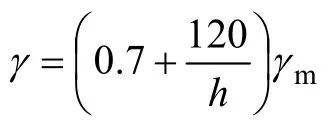
(7) 底座板拉应力容许值取其疲劳破坏容许值[σmax]，其值根据以下疲劳方程确定。

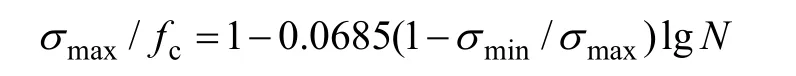
式中：σmax为混凝土最大应力；σmin为混凝土最小应力；fc为混凝土强度；N为荷载循环作用次数。

考虑无砟轨道服役期60 a，荷载循环作用次数1亿次，经计算，底座板疲劳强度允许值为弯拉强度允许值的0.45倍，即1.07 MPa。

(8) 路基允许压应力参考《铁道工务技术手册》取为0.15 MPa。

3 耦合动力学模型验证

由于缺乏路基上CRTS-Ⅱ型无砟轨道振动特性实测数据，而路基上CRTS-Ⅱ型无砟轨道与CRTS-I型无砟轨道具有相似的结构，都由轨道板、CA砂浆及混凝土底座构成，本文以 CRTS-I型无砟轨道振动特性实测结果及西南交通大学相应的理论计算对耦合动力学模型进行验证[14]。

车辆及线路参数见文献[6]。高速动车组行车速度为 200 km/h，用本文建立的列车-路基上板式无砟轨道耦合动力学模型对此工况进行计算，并与遂渝线实测结果[14]与西南交通大学理论计算结果[8]进行对比。

最大钢轨、轨道板、底座垂向振动加速度和垂向位移时程曲线结果见图 2～7；本文计算结果、遂渝线实测结果[14]及文献[6]的理论计算结果对比见表1。

从表1可以看出：本文计算结果与文献[6]中的计算结果及遂渝线实测结果[14]很接近，证明本文三维实体有限元耦合动力学模型是正确的。

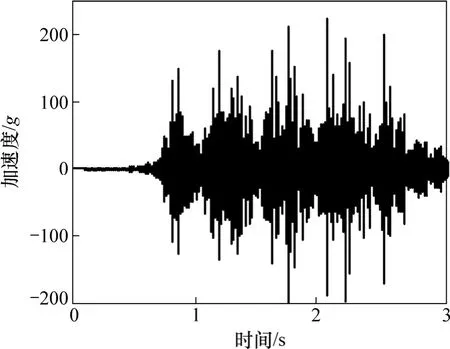
图2 最大钢轨垂向振动加速度时程曲线Fig. 2 Time history of the maximum vertical acceleration of rail

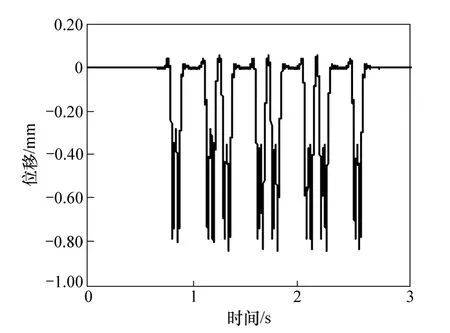
图3 最大钢轨垂向位移时程曲线Fig. 3 Time history of the maximum vertical displacement of rail

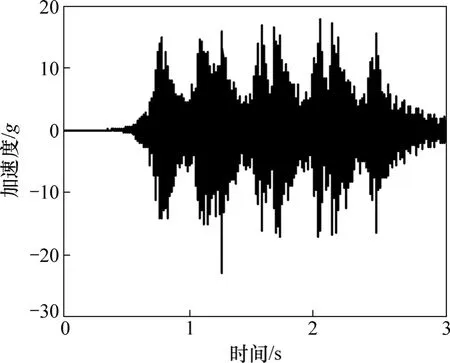
图4 最大轨道板垂向振动加速度时程曲线Fig. 4 Time history of the maximum vertical acceleration of slab

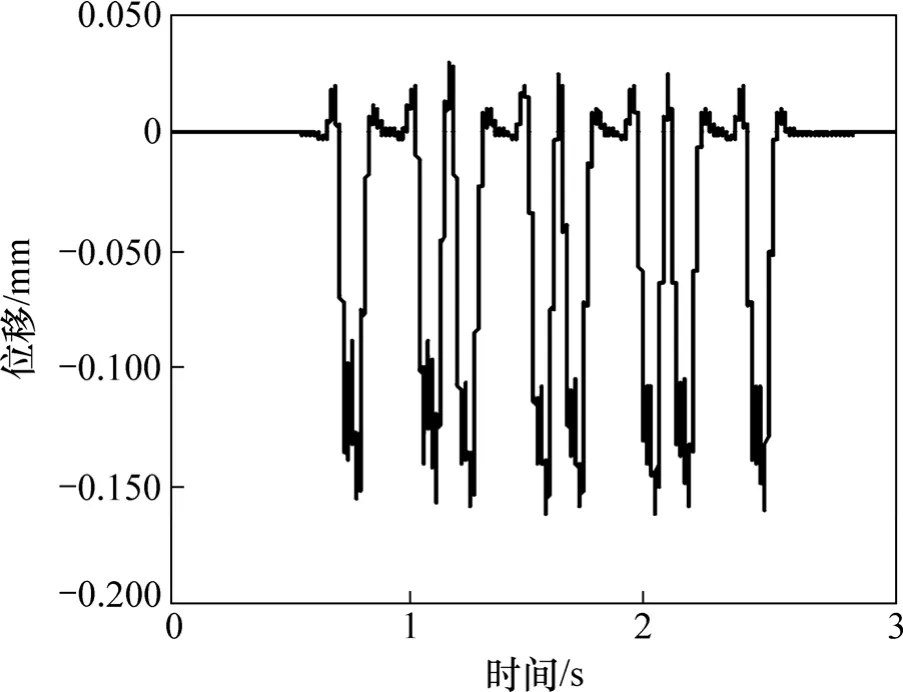
图5 最大轨道板垂向位移时程曲线Fig. 5 Time history of the maximum vertical displacement of slab

图6 最大底座板垂向振动加速度时程曲线Fig. 6 Time history of the maximum vertical acceleration of base plate

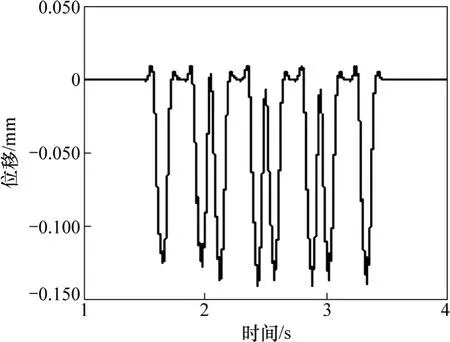
图7 最大底座板垂向位移时程曲线Fig. 7 Time history of the maximum vertical displacement of base plate

表1 计算结果比较Table 1 Comparison of calculated results

4 仿真研究

4.1 仿真计算方案

高速动车组以 350 km/h速度通过路基上CRTS-Ⅱ型板式无砟轨道线路。高速动力组参数见文献[9]，轨道主要计算参数见表2。

考虑自重荷载、轨道中长波随机不平顺、轨道短波随机不平顺、路基不均匀沉降荷载、无砟轨道板温度梯度荷载共同作用，对CRTS-Ⅱ型板式无砟轨道线路路基不均匀沉降限值理论进行研究，共16种工况，见表3。不同工况下仿真计算结果见表4。

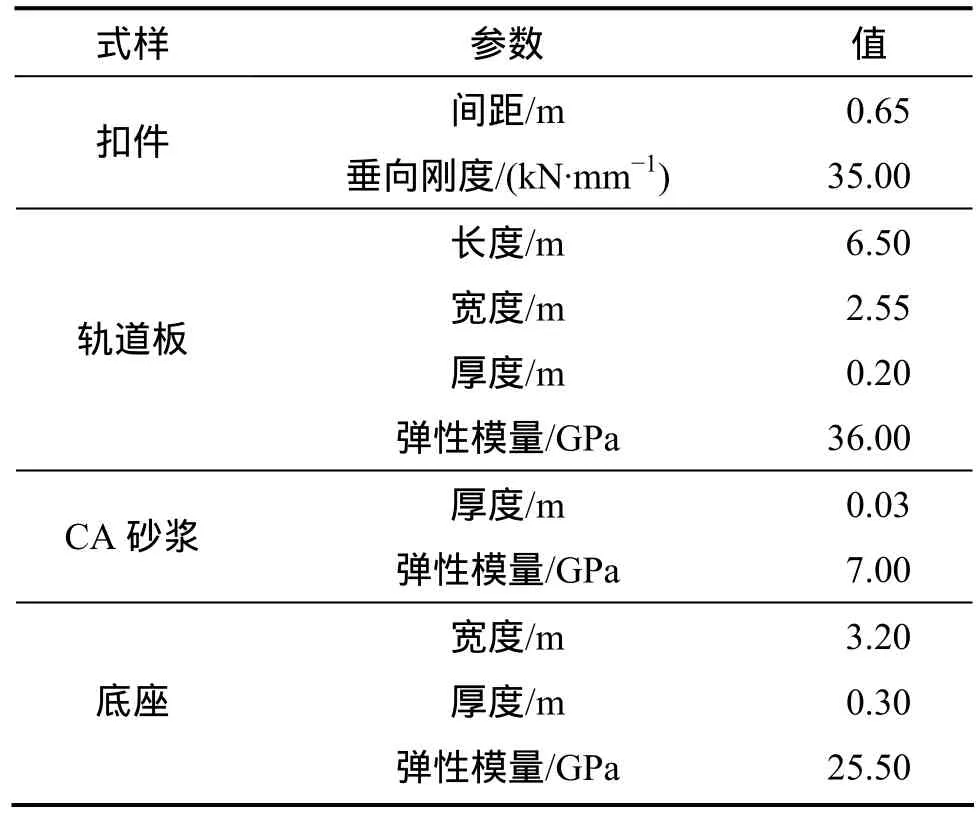
表2 路基上CRTS-Ⅱ型板式无砟轨道计算参数Table 2 Calculation parameters of CRTS-II type slab track on subgrade

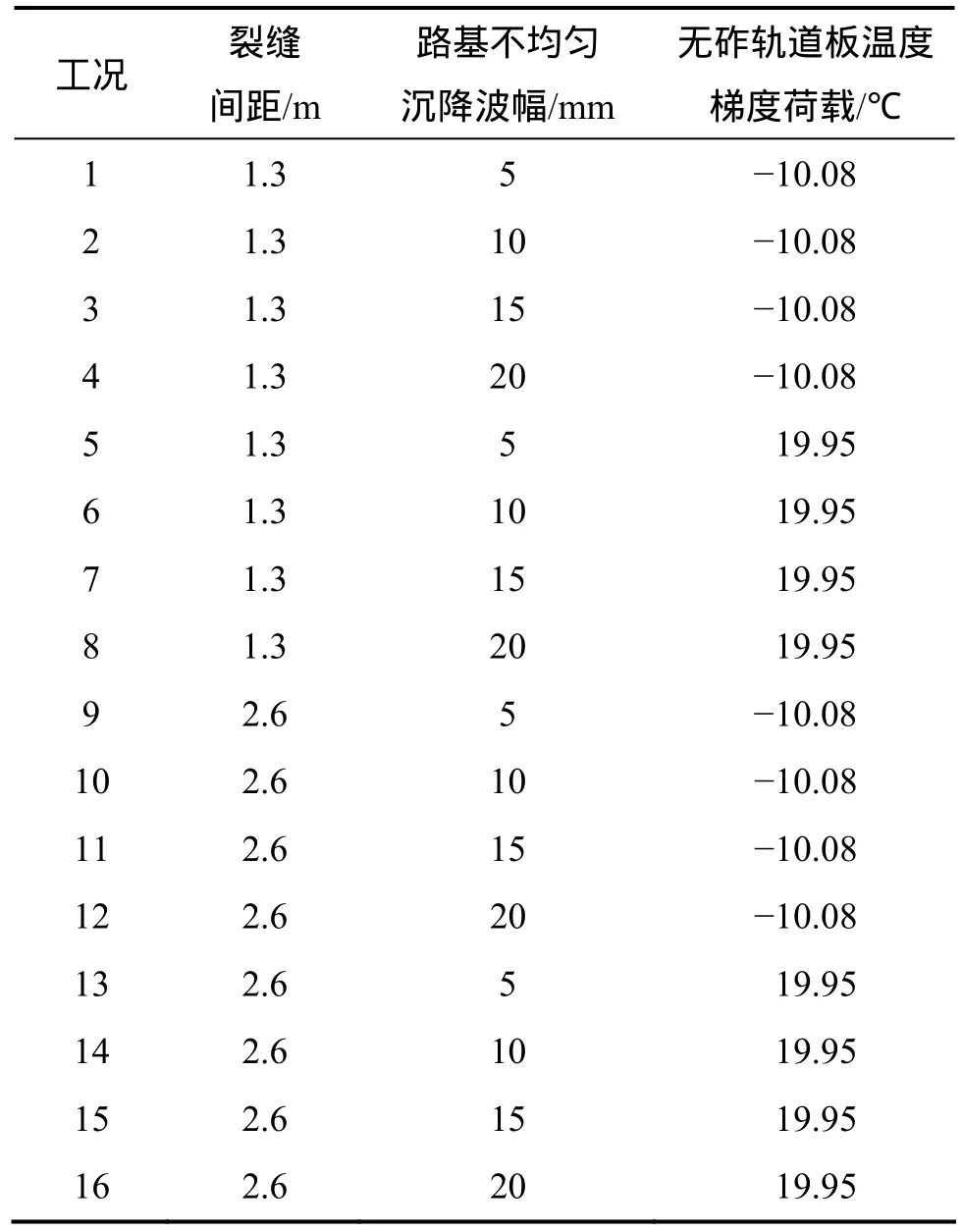
表3 仿真计算方案Table 3 Scheme and plans for simulation

4.2 计算结果及分析

从表4可以看出：

(1) 车体最大振动加速度随着路基不均匀沉降幅值增加而迅速增加，路基不均匀沉降幅值达到 13 mm/20 m(即不均匀沉降波长为13 mm，波幅为20 m)时，车体最大振动加速度达到舒适度限值0.13g。

(2) 最大轮轨力随着路基不均匀沉降幅值增加而有所增加，但其值小于轮轨最大值的允许值300 kN，最大轮轨力不是路基不均匀沉降限值控制因素。

(3) 钢轨最大正弯矩随着路基不均匀沉降幅值增加而有较大增加，但根据《铁路轨道设计规范》相关条文相关规定及附录的相关数据(钢轨横向水平力系数取为 1.25、无缝线路温度应力按 60 ℃钢轨温度变化幅度计算、制动附加力取10 MPa)，考虑路基不均匀沉降的影响，得到钢轨最大应力检算值为 314.4 MPa，仍小于钢轨应力允许值350 MPa，钢轨最大正弯矩不是路基不均匀沉降限值控制因素。

(4) 扣件最大拉力随着路基不均匀沉降幅值增加而大幅增加，且与无砟轨道温度梯度和无砟轨道裂缝间距有很密切的关系：当无砟轨道裂缝间距为 1.3 m时，扣件最大拉力较小，不是路基不均匀沉降限值的控制因素；当无砟轨道裂缝间距为2.6 m且无砟轨道温度梯度为正最大值，路基不均匀沉降幅值达到10 mm/20 m时，扣件最大拉力达到限值12 kN。

(5) 路基不均匀沉降幅值对轨道板纵、横向拉应力影响不大，轨道板纵、横向拉应力远小于其允许值4.42 MPa，不是路基不均匀沉降限值的控制因素。

(6) 当无砟轨道裂缝间距为1.3 m时，底座板纵、横向应力小于底座板疲劳允许应力，不是路基不均匀沉降限值的控制因素；当无砟轨道裂缝间距为 2.6 m且无砟轨道温度梯度为正最大值，路基不均匀沉降幅值达到18 mm/20 m时，底座板纵向应力达到底座板疲劳允许应力1.07 MPa。

(7) 路基不均匀沉降幅值对 CA砂浆、路基最大压应力影响不大，CA砂浆、路基最大压应力远小于各自允许值，不是路基不均匀沉降限值的控制因素。

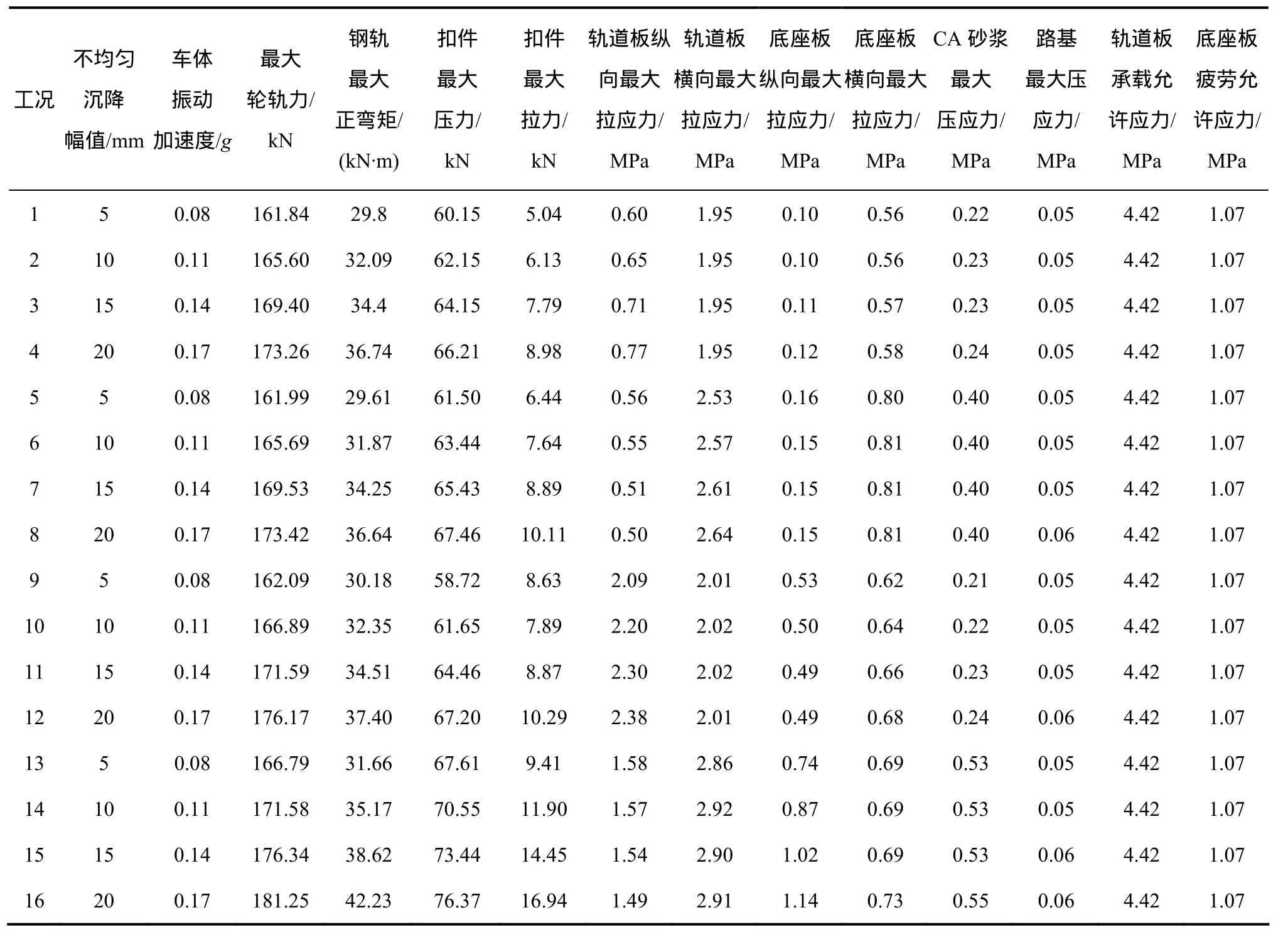
表4 参数计算结果Table 4 Calculation results of parameters

5 结论

(1) 无砟轨道温度梯度荷载对无砟轨道各部件受力均有比较明显的影响。在研究无砟轨道线路路基不均匀沉降限值时，有必要同时考虑无砟轨道温度梯度荷载的影响。

(2) 综合车体和Ⅱ型板式轨道结构动力计算结果，根据相关规范的规定，建议路基上CRTS-Ⅱ型板式无砟轨道线路路基的不均匀沉降限值取为 10 mm/20 m。

(3)无砟轨道线路路基不均匀沉降限值是一个很复杂的问题，本文仅从旅客舒适性及无砟轨道承载力研究CRTS-Ⅱ型板式无砟轨道线路路基不均匀沉降限值。下一步拟改进现有轨轨关系模型，考虑轮轨间多点接触、轮轨间蠕滑力非线性特性，同时考虑对列车横向振动有很大影响的风荷载的共同作用，从行车安全角度对路基不均匀沉降限值进行深入研究。

[1] 徐庆元. 高速铁路无砟轨道国产化理论研究[R]. 天津:铁道第三勘察设计集团有限公司博士后工作站, 2008: 25-41.

XU Qingyuan. Calculation theory for designing home-made ballastless track of high speed railway[D]. Tianjin: Post Doctoral Research Station of the Third Railway Survey and Design Group Corporation, 2008: 25-41.

[2] 陈鹏. 高速铁路无砟轨道结构力学特性的研究[D]. 北京: 北京交通大学土木工程学院, 2008: 66-73.

CHEN Peng. Research on mechanical characteristics of ballastless track in high-speed railway[D]. Beijing: Beijing Jiaotong University. School of Civil Engineering, 2008: 66-73.

[3] 蔡成标, 徐鹏. 高速铁路无砟轨道关键设计参数动力学研究[J]. 西南交通大学学报, 2010, 45(4): 493-497.

CAI Chengbiao, XU Peng. Dynamic analysis of key design parameters for ballastless track of high-speed railway[J]. Journal of Southwest Jiaotong University, 2010, 45(4): 493-497.

[4] 蔡成标, 翟婉明, 王开云. 遂渝线路基上板式轨道动力性能计算及评估分析[J]. 中国铁道科学, 2006, 27(4): 17-21.

CAI Chengbiao, ZHAI Wanming, WANG Kaiyun. Calculation and assessment analysis of the dynamic performance for slab track on Sui—Yu Railway[J]. China Railway Science, 2006,27(4): 17-21.

[5] Steenbergen M J M M, Metrikine A V, Esveld C. Assessment of design parameters of a slab track railway system from a dynamic viewpoint[J]. Journal of Sound and Vibration, 2007, 306(1):361-371.

[6] 赫丹, 向俊, 曾庆元. 一种无碴轨道动力学建模的新方法[J].中南大学学报: 自然科学版, 2007, 38(6): 1206-1211.

HE Dan, XIANG Jun, ZENG Qingyuan. A new method for dynamics modeling of ballastless track[J]. Journal of Central South University: Science and Technology, 2007, 38(6):1206-1211.

[7] 罗震. 高速铁路无砟轨道结构受力及轮轨动力作用分析[D].成都: 西南交通大学列车与线路研究所, 2008: 68-79.

LUO Zhen. Analysis of structure mechanics and wheel/rail dynamic interaction of ballastless track in high-speed railway[D].Chengdu: Southwest Jiaotong University. Train & Track Research Institute, 2008: 68-79.

[8] 石现峰, 宣言, 王澜. 土质路基上板式无砟轨道结构的动力学性能仿真研究[J]. 中国铁道科学, 2008, 29(4): 15-20.

SHI Xianfeng, XUAN Yan, WANG Lan. Simulation research on the dynamic characteristics of slab ballastless track structure on soil subgrade[J]. China Railway Science, 2008, 29(4): 15-20.

[9] 翟婉明. 车辆-轨道耦合动力学[M]. 2版. 北京: 中国铁道出版社, 2002: 146-147.

ZHAI Wanming. Vehicle-track coupling dynamics[M]. 2nd ed.Beijing: China Railway Press, 2002: 146-147.

[10] 陈泽深, 王成国. 铁道车辆动力学与控制[M]. 北京: 中国铁道出版社, 2004: 25-41.

CHEN Zeshen, WANG Chengguo. Railway vehicle dynamics and control[M]. Beijing: China Railway Press, 2004: 25-41.

[11] Sato Y. Study on high-frequency vibration in track operation with high-speed trains[J]. Quarterly Reports, 1977, 18(3):109-114.

[12] 徐志胜. 轨道交通轮轨噪声预测与控制的研究[D]. 成都: 西南交通大学牵引动力国家重点实验室, 2004: 42-56.

XU Zhisheng. Prediction and control of wheel/ rail noise for rail transit[D]. Chengdu: Southwest Jiaotong University. Traction Power State Key Laboratory, 2004: 42-56.

[13] 李秀梅, 吴锋, 黄哲华. PCG法的理论解释及在结构分析中的应用[J]. 广西大学学报: 自然科学版, 2009, 34(4): 463-468.

LI Xiumei, WU Feng, HUANG Zhehua. Theoretical explanation for PCG method and its application in structural analysis[J].Journal of Guangxi University: Natural Science and Technology,2009, 34(4): 463-468.

[14] 西南交通大学列车与线路研究所. 遂渝线路基地段无砟轨道动力性能测试研究报告[R]. 成都: 西南交通大学列车与线路研究所, 2007: 11-18.

Train & Track Research Institute of Southwest Jiaotong University. Experiment report of dynamic characteristic of ballastless on subgrade of Sui—Yu test section[R]. Chengdu:Southwest Jiaotong University. Train & Track Research Institute,2007: 11-18.