线性分布荷载作用下双模量简支梁的Kantorovich解
2013-09-12吴晓黄翀孙晋
吴晓,黄翀,孙晋
(湖南文理学院 土木建筑工程学院,湖南 常德,415000)
在工程实际中,石墨、增强复合材料、金属合金、陶瓷、玻璃、铸铁等许多材料都具有拉压弹性模量不同的双模量性质,所以,用双模量本构关系对这些材料制成的结构进行计算分析已备受关注[1-3]。对于拉压弹性模量不同的双模量材料,弹性系数不仅依赖于结构材料,而且与结构材料、形状、边界条件及外载荷有关[4-6]。在梁、弹性平面等问题的结构中,人们考虑了材料的双模量特性[7-10],并采用Kantorovich法研究了柱形杆的扭转问题,但未见采用Kantorovich法研究双模量简支梁的平面应力问题的报道。经典弹性理论研究线性分布荷载作用下简支梁的平面应力问题多采用半逆法或三角级数法,而采用半逆法时需要确定的待定常数较多,采用三角级数法时存在收敛慢且计算过程复杂繁琐等缺陷。为此,本文作者采用Kantorovich法研究在线性分布荷载作用下双模量简支梁的平面应力问题。
1 材料力学应力表达式
由于双模量梁在外荷载作用下弯曲时,会形成弹性模量不同的拉伸区和压缩区,由弹性理论可知双弹性模量梁弯曲时的应力和应变关系为:
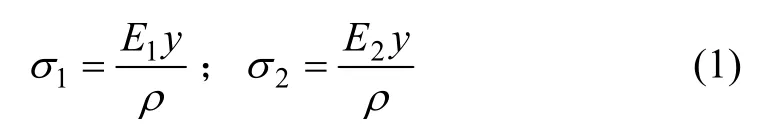
式中:σ1为拉伸区应力;σ2为压缩区应力;E1为拉伸区的弹性模量;E2为压缩区的弹性模量;y为计算点至中性轴的距离;ρ为中性层的曲率半径。
据弹性理论,双模量梁弯曲时横截面内力应满足以下关系:
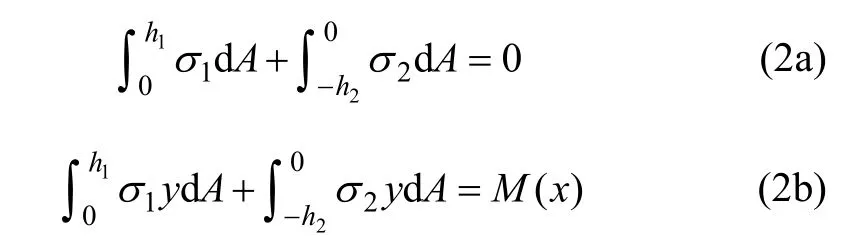
将式(1)代入(2)可得:
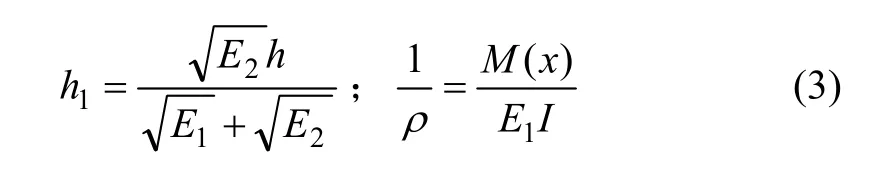
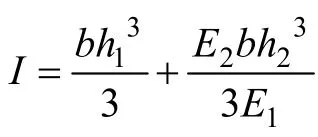
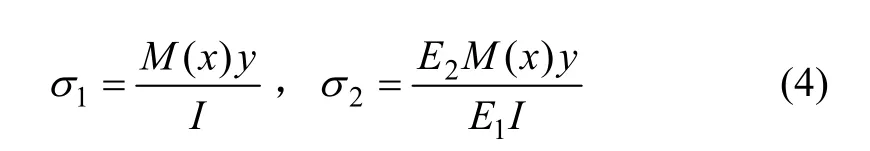
图1中,双模量简支梁中点处的弯矩为
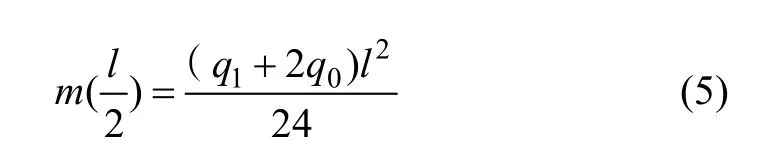
式中:q0为梁上线性分布载荷最小值;q1为梁上线性分布载荷最大值;l为梁的跨长。
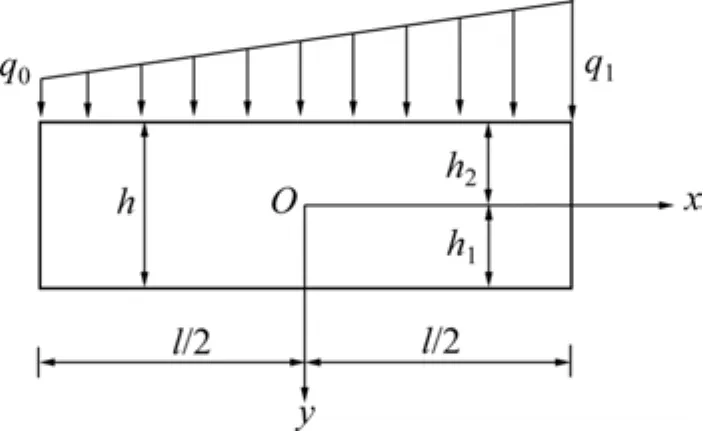
图1 双模量简支梁Fig.1 Bimodulous simply supported beam
因此,图1 中双模量简支梁中点处的最大拉应力σ1及最大压应力σ2分别为:
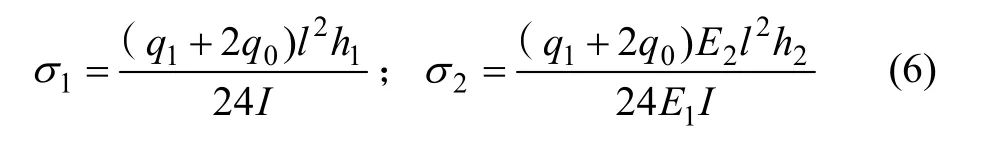
2 简支梁的Kantorovich解
对于图1所示线性分布荷载作用下的双模量简支梁,其线性分布荷载的集度表达式为
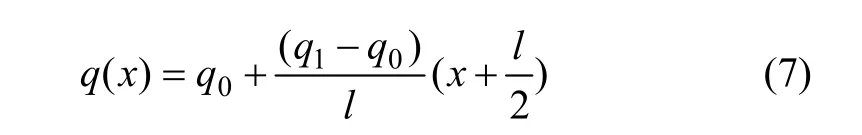
双模量简支梁上下面边界条件及中性轴上的应力条件分别为:
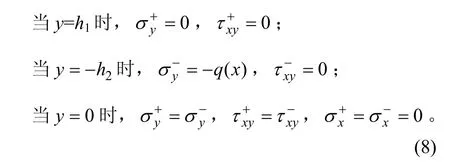
假设线性分布荷载作用下双模量简支梁受拉区应力函数φ1(x,y)和受压区应力函数φ2(x,y)分别为:

式中:Y1(y)为梁拉伸区变量y的贡献函数;Y2(y)为梁压缩区变量y的贡献函数。
则线性分布荷载作用下双模量简支梁的应力表达式为:
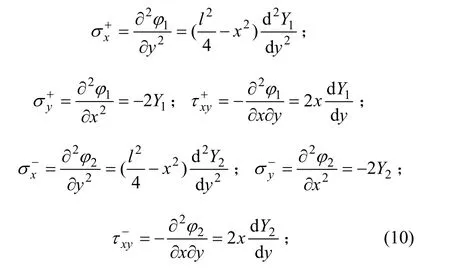
式中:“+”表示拉伸区;“-”表示压缩区。
对于平面应力问题,线性分布荷载作用下双模量简支梁的余能为
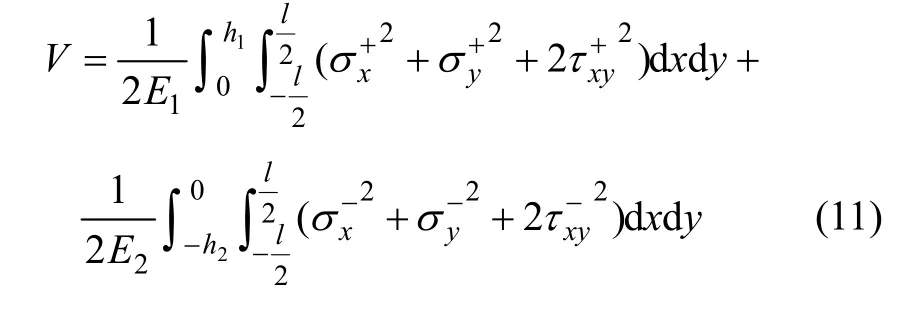
将式(10)代入式(11)可得:
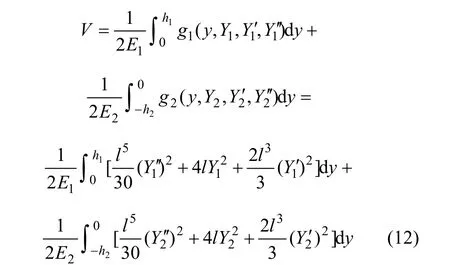
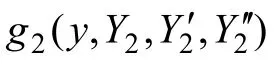
对式(12)进行一阶变分可得:
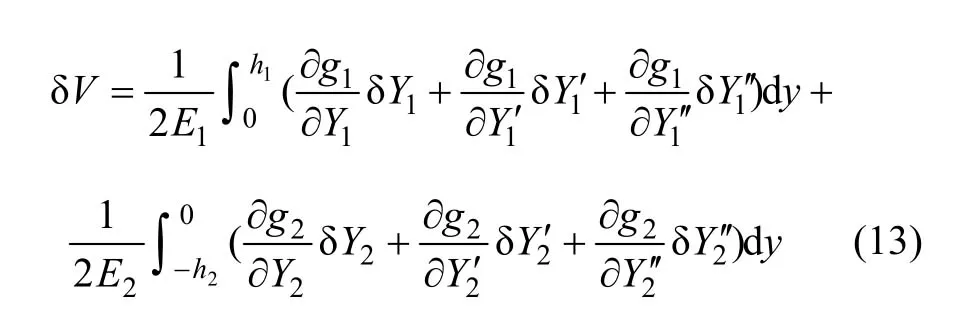
利用微分符号与变分符号可交换性及边界条件式(8)可得:
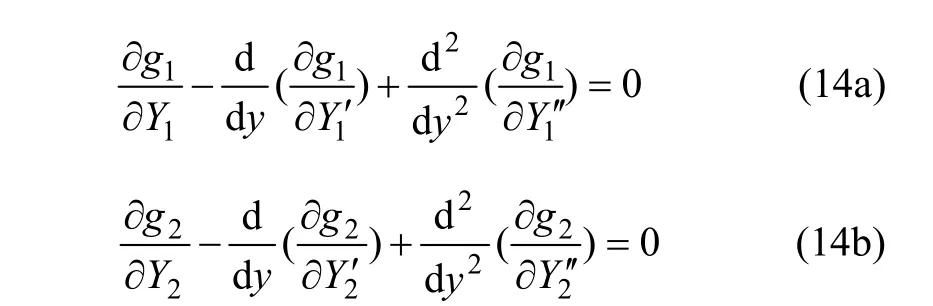
将函数g1(y,Y1,Y1′,Y1′′) 和g2(y,Y2,Y2′,′ )表达式代入式(8)得:
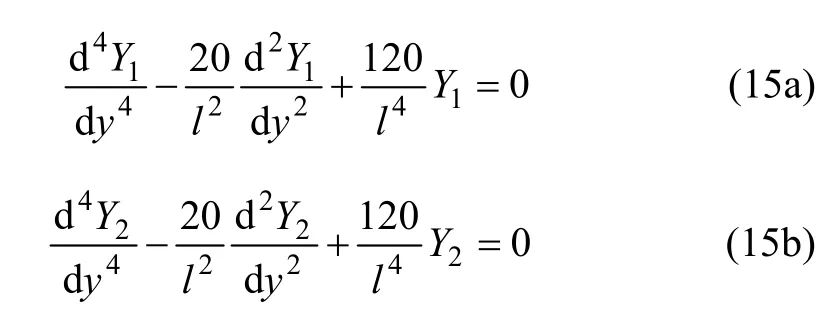
由式(15)可以求得Y1(y)和Y2(y)的表达式:
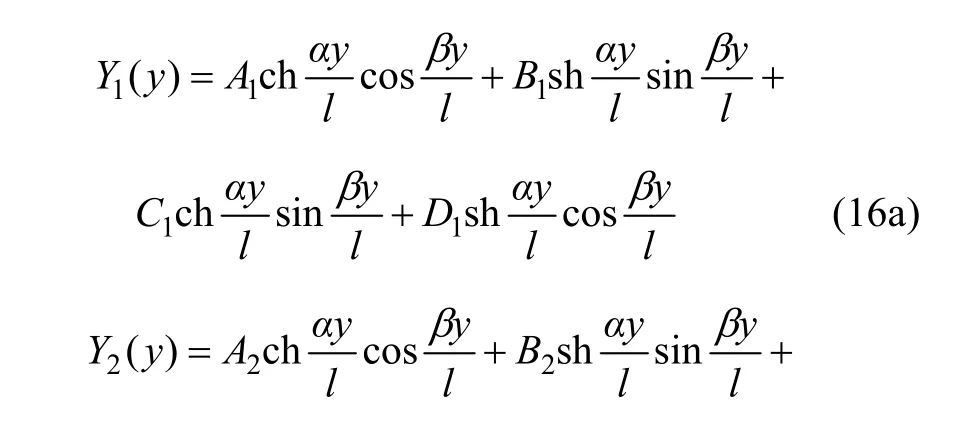
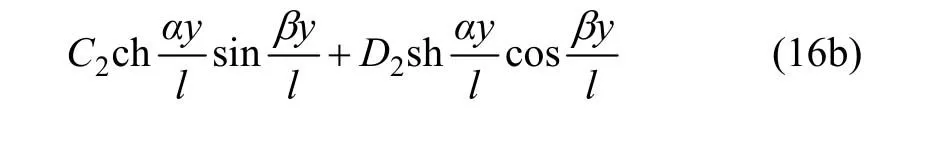
将式(16)代入式(10)可求得拉伸区及压缩区应力表达式为:
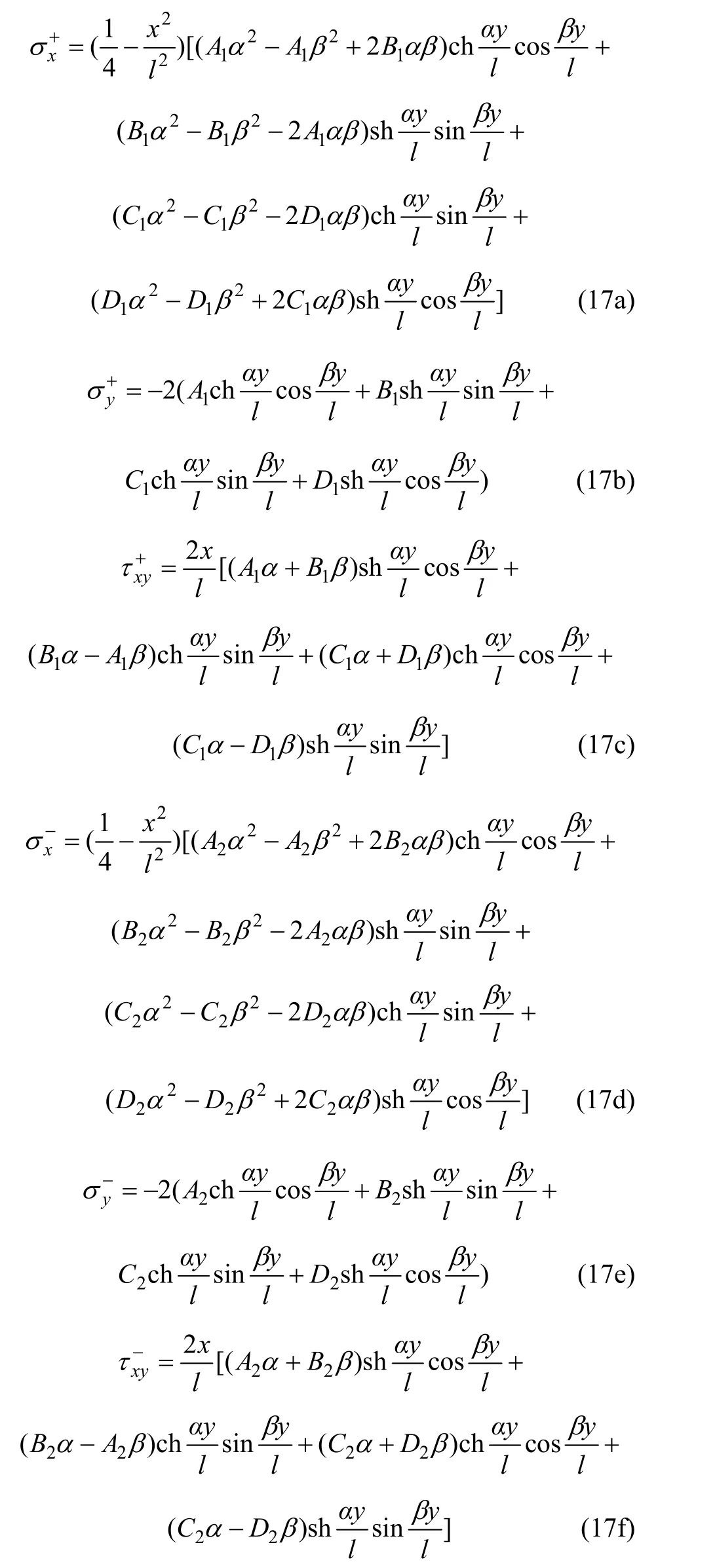
利用式(17)及边界条件式(8)可得:
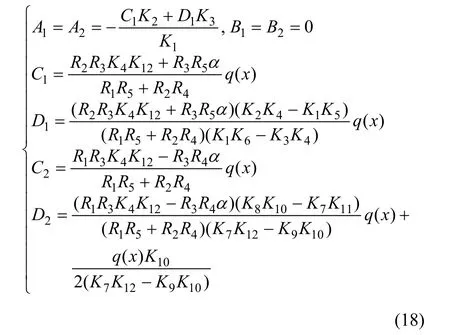
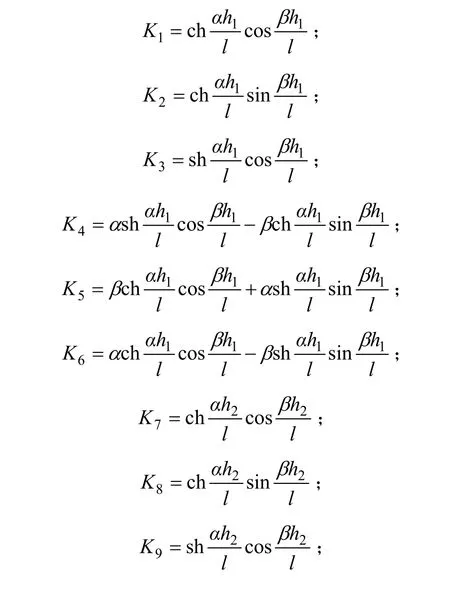
常数K1,K2,K3,K4,K5,K6,K7,K8,K9,K10,K11,K12,R1,R2,R3,R4和R5分别为:
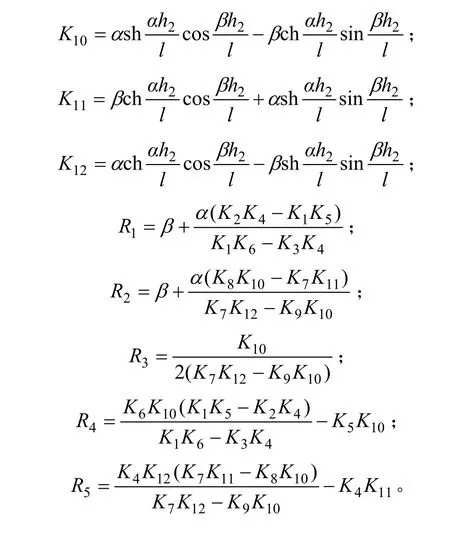
3 算例分析与讨论
首先采用有限元法检验本文 Kantorovich解的计算精度。假设某双模量简支梁的b=1,E1=93.2 GPa,E2=124.36 GPa,采用式(17)和(6)及有限元法计算双模量简支梁中点处的最大拉应力及最大压应力。其中:采用有限元建立双模量简支梁实体模型,模型由2层梁组成,梁高为100 mm,其中上层梁高46.4 mm,材料模型为mat1,E2=124.36 GPa;下层梁高为53.6 mm,材料模型为 mat2,E1=93.2 GPa。单元为 8节点SOLID185单元。具体的计算结果见表1~4。其中:q0和q1见图1;σ1为采用材料力学计算的最大拉应力;σ2为采用材料力学计算的最大压应力。
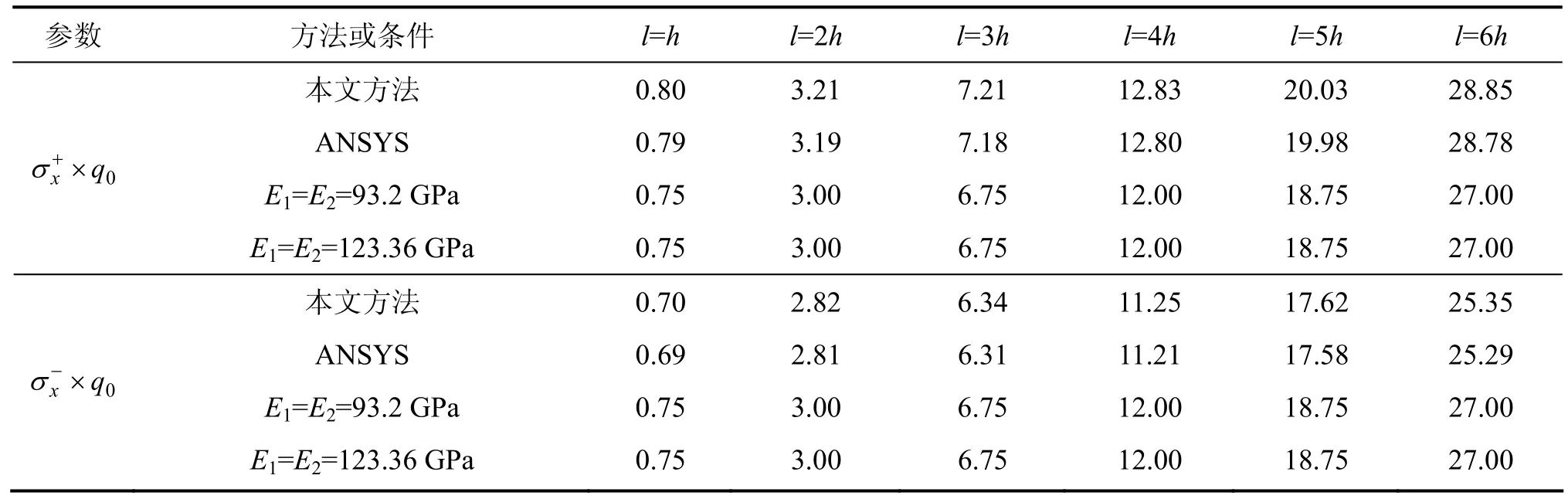
表1 q1=q0时采用本文方法所得双模量简支梁中点处弯曲应力Table 1 Bending stress of bimodulous simply supported beam at midpoint obtained by method in the paper at q1=q0 MPa
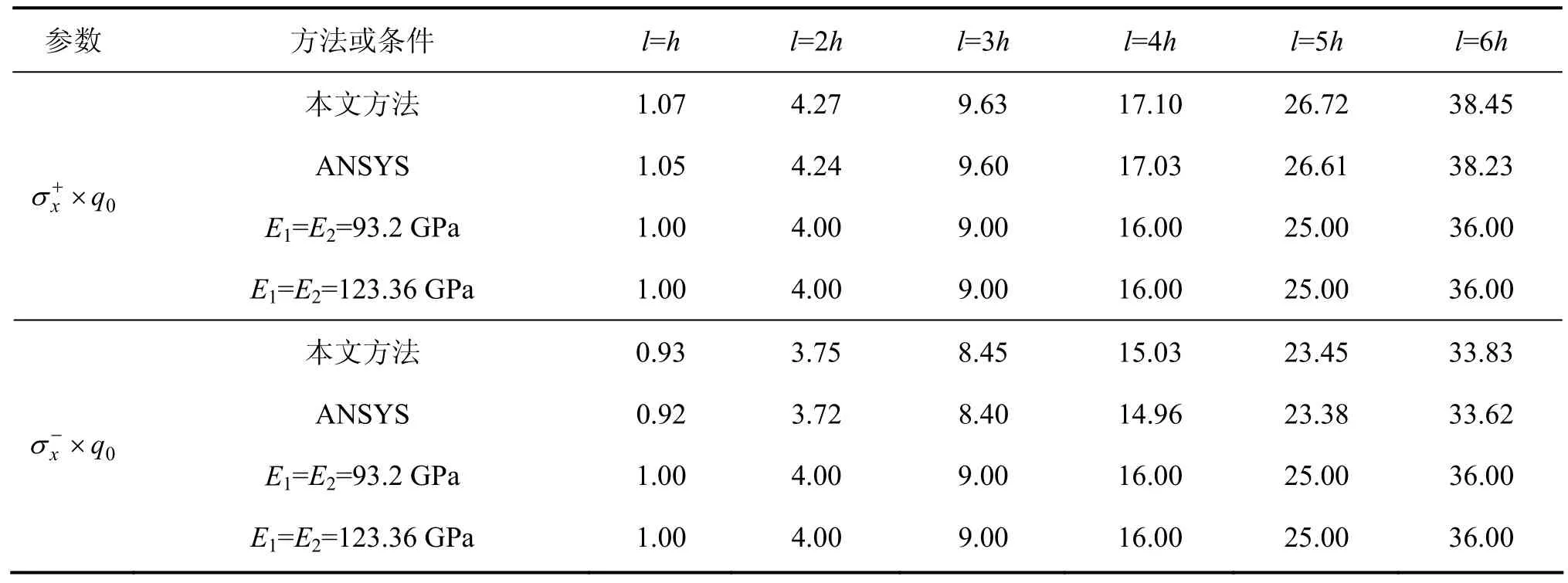
表2 q1=2q0时采用本文方法所得双模量简支梁中点处弯曲应力Table 2 Bending Stress of bimodulous simply supported beam at midpoint obtained by method in the paper at q1=2q0 MPa
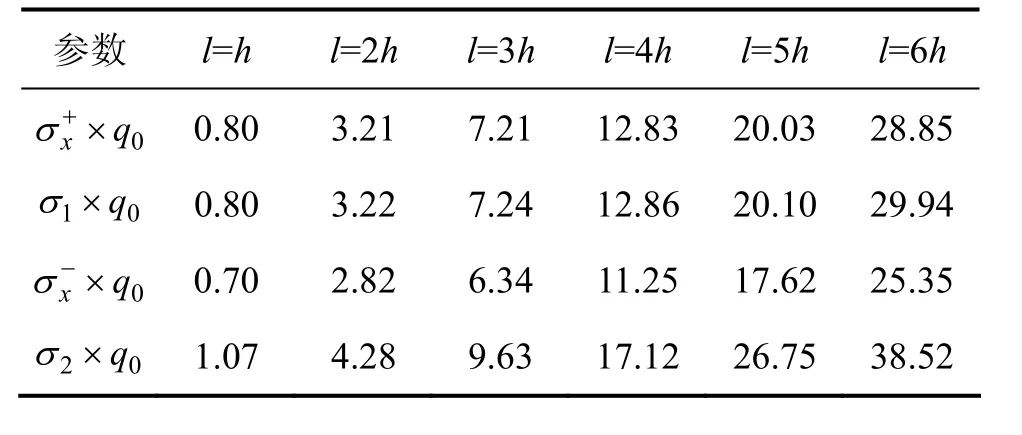
表3 q1=q0时采用材料力学方法所得双模量简支梁中点处弯曲应力Table 3 Bending Stress of bimodulous simply supported beam at midpoint obtained by method of material mechanics at q1=q0 MPa
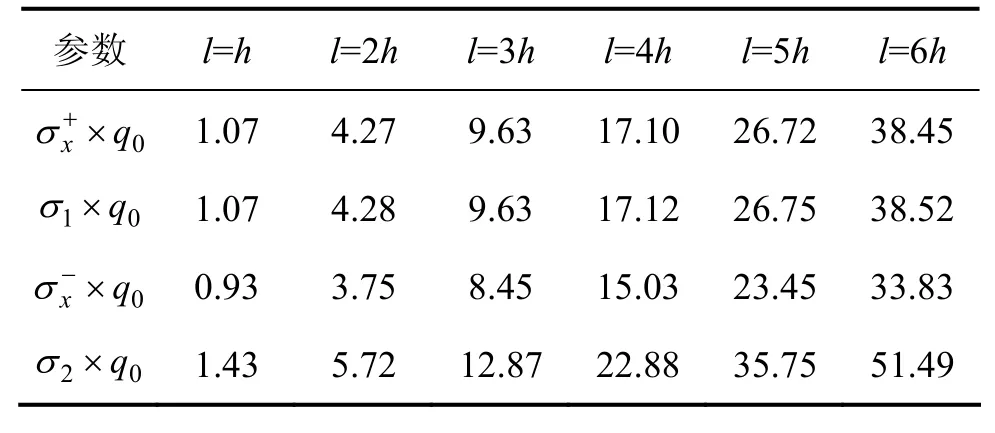
表4 q1=2q0时采用材料力学方法所得双模量简支梁中点处弯曲应力Table 4 Bending Stress of bimodulous simply supported beam at midpoint obtained by method of material mechanics at q1=2q0 MPa
由表1~2中本文方法与ANSYS计算结果的比较可知:采用Kantorovich法研究双模量简支梁中点处弯曲应力的计算结果与有限元法的计算结果很接近,这说明采用 Kantorovich法研究双模量简支梁弯曲应力的计算精度高,所得双模量简支梁的应力公式是可靠的。
由表1~2中采用相同弹性模量弹性理论计算结果与采用双模量弹性理论计算结果的比较可知:采用相同弹性模量弹性理论得到双模量简支梁中点处弯曲应力,与采用双模量弹性理论得到双模量简支梁中点处弯曲应力的误差均在 5%以上。采用相同弹性模量弹性理论研究双模量简支梁的弯曲应力,拉压区的弯曲应力绝对值相等。事实上,双模量简支梁的拉压区的弯曲应力绝对值不相等,随双模量简支梁拉压区的弹性模量变化而变化。在本文中,双模量简支梁的拉压区的弯曲应力相差均达10%以上,所以,对于双模量简支梁的平面应力问题,不宜采用相同弹性模量弹性理论求解,而应该采用双模量弹性理论求解。
由表1~2可知:在外载荷作用下,随着双模量简支梁长高比的增大,双模量简支梁的拉压区的弯曲应力也随着增大。因为随着双模量简支梁长高比的增大,将导致线性分布荷载对双模量简支梁产生的弯矩也相应增大。
比较表1与表2中的计算结果可知:在线性分布荷载(q1=2q0)作用下,双模量简支梁中点处的弯曲应力要大于在均布载荷(q1=q0)作用下双模量简支梁中点处的弯曲应力。这是因为线性分布荷载对双模量简支梁产生的弯矩大于均布载荷对双模量简支梁产生的弯矩。
本文方法计算结果与材料力学方法计算结果见表3和表4。从表3和表4可以看出:采用材料力学方法研究双模量简支梁的弯曲应力,得到的双模量简支梁拉伸区的弯曲应力与本文 Kantorovich法得到的双模量简支梁拉伸区的弯曲应力很接近;但是,采用材料力学方法得到的双模量简支梁的弯曲应力与本文Kantorovich法得到的双模量简支梁压缩区的弯曲应力相差很大,相对误差均在50%以上,并且有限元法的计算结果也证明了这一点。这说明采用材料力学方法研究双模量简支梁的弯曲应力有其局限性。
4 结论
(1) 采用Kantorovich法研究双模量简支梁弯曲应力的计算精度高,所得双模量简支梁的应力公式是可靠的。
(2) 采用材料力学方法研究双模量简支梁的弯曲应力有其局限性。对于双模量简支梁的平面应力问题,不宜采用相同弹性模量弹性理论求解,而应该采用双模量弹性理论求解。
(3) 在外载荷作用下,随着双模量简支梁长高比的增大,双模量简支梁的拉压区的弯曲应力也随着增大;在线性分布荷载作用下,双模量简支梁的弯曲应力大于在均布载荷作用下双模量简支梁的弯曲应力。
[1] Medri G. A nonlinear elastic model for isotropic materials with different behavior in tension and compression[J]. Transactions of the ASME, 1982, 104(1): 26-28.
[2] Bert C W, Reddy J N, Chao W C, et al. Vibration of thick rectangular plates of bimodulous composite material[J]. Journal of Applied Mechanics, 1981, 48(2): 371-376.
[3] Srinivasan R S, Ramachandra L S. Axisymmetric nonlinear dynamic response of bimodulous annular plates[J]. Journal of Vibration and Acoustics, 1990, 112(2): 202-205.
[4] 李战莉, 黄再兴. 双模量泡沫材料等效弹性模量的细观力学估算方法[J]. 南京航空航天大学学报, 2006, 38(4): 464-468.
LI Zhanli, HUANG Zaixing. Meso-mechanical method for estimating equivalent elastic modulus of foam-solid with double-modulus[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2006, 38(4): 464-468.
[5] 曾纪杰. 对中柔度压杆的双模量理论的修正[J]. 机械强度,2006, 28(3): 462-464.
ZENG Jijie. Revision of the formula with bimodulusim intermediate column[J]. Journal of Mechanical Strength, 2006,28(3): 462-464.
[6] 蔡来生, 俞焕然. 拉压模量不同弹性物质的本构[J]. 西安科技大学学报, 2009, 29(1): 17-21.
CAI Laisheng, YU Huanran. Constitutive relation of elastic materials with different elastic moduli in tension and compression[J]. Journal of Xi'an University of Science and Technology, 2009, 29(1): 17-21.
[7] 吴晓, 杨立军, 孙晋. 双模量圆板弯曲变形的计算分析[J]. 西安建筑科技大学学报: 自然科学版, 2009, 41(1): 88-92.
WU Xiao, YANG Lijun, SUN Jin. Bending deformation calculation of bimodulous circular plate[J]. Journal of Xi'an University of Architecture & Technology: Natural Science Edition, 2009, 41(1): 88-92.
[8] 罗战友, 夏建中, 龚晓南. 不同拉压模量及软化特性材料的柱形孔扩张问题的统一解[J]. 工程力学, 2008, 25(9): 79-84.
LUO Zhanyou, XIA Jianzhong, GONG Xiaonan. Unified solution for expansion of cylindrical cavity in strain-softening materials with different elastic moduli in tension and compression[J]. Engineering Mechanics, 2008, 25(9): 79-84.
[9] 阿巴尔楚米扬. 不同模量弹性理论[M]. 邬瑞锋, 张允真, 译.北京: 中国铁道出版社, 1986: 11-22.
Ambartsumyan S A. Elasticity theory of different modulus[M].WU Ruifeng, ZHANG Yunzhen, transl. Beijing: China Railway Press, 1986: 11-22.
[10] 高潮, 刘相斌, 吕显强. 用拉压不同模量理论分析弯曲板[J].计算力学学报, 1998, 15(4): 448-455.
GAO Chao, LIU Xiangbin, LÜ Xianqiang. Analysis for the plate with the theory of different extension compression elastic modulis[J]. Chinese Journal of Computaional Mechanics, 1998,15(4): 448-455.
