干湿交替作用下氯离子在开裂混凝土中的输运规律

延永东 ，金伟良，王海龙，陆春华

(1. 江苏大学 土木工程与力学学院，江苏 镇江，212013；2. 浙江大学 结构工程研究所，浙江 杭州，310058)

在氯盐侵蚀环境中，干湿交替区域对应有害介质侵蚀最为严重的结构部位，是混凝土结构耐久性设计的关键[1-2]，但是，国内外对此研究均是基于完好的混凝土结构进行的。而对于服役混凝土结构来说，各种原因造成的裂缝是不可避免的[3]。裂缝的存在加速了氯离子在附近混凝土内的传输，使部分区域的氯离子提前达到阈值，钢筋提前锈蚀，从而降低结构的使用寿命[4]，因此，有必要进行干湿交替作用下氯离子在开裂混凝土中的侵蚀研究。相对于完好混凝土结构来说，裂缝的存在为计算氯离子在混凝土内的传输增加了一定难度，而干湿循环传输机理的复杂性更增大了计算难度。双重孔隙介质模型是一种等效计算开裂物质的有效方法，在计算水分传输或有害物质的侵蚀时，既能简化分析过程，又能得到比较精确的结论。本研究根据干湿交替情况下水分在混凝土中的渗流机理，采用双重孔隙介质模型，建立在浓度梯度和孔隙液饱和度梯度耦合作用下的氯离子在混凝土和裂缝内的输运方程，然后利用有限单元法进行数值模拟分析，并设计相应的试验进行验证。

1 双重孔隙介质模型

双重孔隙介质模型最早由Barrenblatt于20世纪60年代提出[5]，此后在裂隙岩体渗流工程和油藏工程中得到了广泛应用[6-7]。由于岩体与混凝土均为多孔介质，具有相似的内部结构，且岩体裂缝与开裂混凝土内的宏观裂缝具有相同的尺度(10-2～100mm)，因此，本研究借鉴该模型分析氯离子在开裂混凝土中的传输。

在双重孔隙介质模型中，除混凝土及其自身固有的微裂缝为多孔介质外，宏观裂缝也被等效为多孔介质，只是其孔隙率要远大于混凝土，如图1所示。在计算氯离子在混凝土内的侵蚀时，需分别计算氯离子在混凝土和裂缝内的输运及其之间的相互影响。如在湿润过程中，氯离子在裂缝中的传输速度大于在混凝土内的传输速度，从而在相同深度处，裂缝与混凝土之间存在浓度差，部分氯离子会由裂缝向混凝土内迁移。而在干燥过程中，这一过程正好相反，部分区域的氯离子会随水分从混凝土向裂缝迁移。为了简化计算，进行如下假设：

图1 双重孔隙介质模型等效原理Fig.1 Schematic of dual porous medium model

(1) 不考虑水对混凝土孔隙和裂缝结构的影响；

(2) 不考虑混凝土裂缝的自愈合效应。

由于干湿循环作用下孔隙水在非饱和混凝土内的流动是氯离子输运的基础，因此，本研究首先建立水分在开裂混凝土内的输运模型，然后，在此基础上建立氯离子的输运方程。

2 水分在开裂混凝土内的输运模型

采用双重孔隙介质模型，可将水分在混凝土和宏观裂缝内的传输看作在多孔介质内的传输，只是渗透系数不同。由于氯离子在裂缝与混凝土内的扩散均与孔隙水饱和度有关，因此，为了方便计算，将水分在混凝土与裂缝内的渗流均表示为孔隙(裂缝)水饱和度的形式。

2.1 水分在混凝土内输运模型

非饱和状态下水分在混凝土内的运输机理非常复杂，涉及到扩散、毛细管效应和渗透效应，为了便于工程应用，本研究根据已有文献，采取1个统一的非线性水分运输模型来描述混凝土中水分的运输规律[8-10]。

式中：s为混凝土孔隙饱和度；D(s)为包含液态水分和水蒸气的水分扩散系数，是孔隙结构特征与饱和度的非线性函数，根据文献[11]，D(s)=K(s) ∂p/ ∂s。

2.2 水分在裂缝内的输运模型

不同压力梯度下水分在裂缝内的输运可用扩展的非线性达西定律表示[12]：

式中：ucr为裂缝处的水的渗流速度(m/s)；Kcr(s)为裂缝内的水分渗透系数(m/s)，是裂缝内饱和度的非线性函数；p为压力，一般用压力水头表示。式(2)可变换为与饱和度有关的扩散方程：

式中：Dcr(s)为裂缝内的水分扩散系数，与裂缝宽度的分布及裂缝饱和度有关，同理，Dcr(s)=Kcr(s) ∂p/ ∂s。

2.3 水分在混凝土和裂缝内的扩散系数

多孔介质和裂缝内的水分渗透系数、扩散系数与孔隙结构分布有关，在非饱和状态下，只有较小的孔隙和裂缝才能保持水分，起到运输水分的作用。假设混凝土孔隙半径和裂缝宽度均服从 Rayleigh-Ritz分布，则对应半径为r的孔隙(裂隙)体积占总孔隙(裂隙)体积分数为：

由此可得：

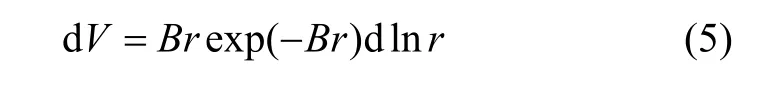
式中：B为Rayleigh-Ritz分布参数，为所占体积分数最大的孔隙半径的倒数，对普通混凝土，可取B=107(1/m)[13]，对裂缝，B=2/w(1/m)(其中：w为平均裂缝宽度[14])。对一般 V形裂缝，可取表面裂缝宽度的一半。开裂混凝土的孔隙结构分布如图2所示。

图2 双重孔隙介质结构模型Fig. 2 Structural model of dual porous medium

在非饱和状态下，孔隙液的渗流只发生在饱和孔隙结构中，忽略气态水分在非饱和孔隙中的输运，并综合考虑孔隙弯曲度等影响，液态水分渗透系数Kl可以简化为[13]：

式中：ρ为液态水分的密度(kg/m3)；η为液态水分的黏滞性系数(Pa·s)；φ为孔隙率(%)；rc为 Kelvin平衡半径(为了简化模型计算，本研究假设混凝土中的孔隙和裂缝均为变直径的圆柱形)。由液体张力平衡的Laplace方程得到：

式中：γ为液体表面张力(N/m)；rs为未考虑孔隙吸附水膜厚度的孔隙半径(m)；θ为水分和混凝土基体的接触角；C为比例系数。

由此可得到与孔隙压力有关的液态水分渗透系数：

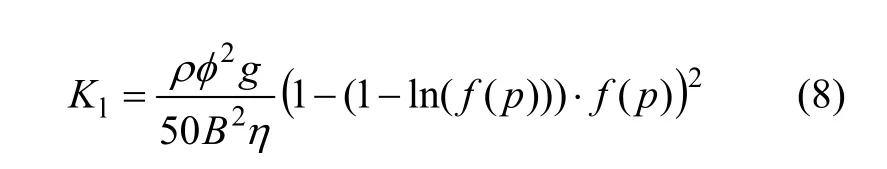
式中：f(p)=exp(2BCγcos(θ)/p)；g为重力加速度(m/s2)。

由于水分在干燥和湿润过程中存在墨水瓶效应，水分渗入和蒸发过程中饱和度s与孔隙压力p的关系有所不同，分别如下[16]。

渗入过程：

干燥过程：

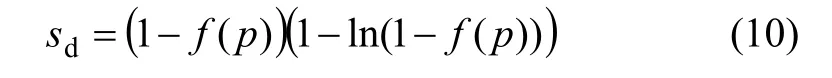
渗入过程：

干燥过程：

其中：g(p)=lambertw( -s/e)是方程g(p)exp(g(p))=-s/e 的解[17]。

根据上面分析可计算出混凝土内和不同宽度裂缝内的饱和度和渗透系数随毛细压力的变化关系曲线。计算中，分别取平均裂缝宽度为0.01，0.05和0.2 mm，结果如图3和4所示。由图3可看出：相同毛细压力下混凝土内的饱和度远大于宏观裂缝内的饱和度，且宏观裂缝内的饱和度随裂缝宽度增大而减小。由图 4可看出：在非饱和状态下，混凝土内的水力扩散系数大于宏观裂缝内的水力扩散系数，裂缝内的水力扩散系数随裂缝宽度增大而减小，而在饱和状态下正好相反。这一结果与Boulfiza等[18]得到的结果相似。

2.4 耦合条件

由于水分在裂缝和混凝土内的渗透系数不同，因此，在湿润过程中，裂缝内的部分水分会渗入混凝土，而在干燥过程中，混凝土内的部分水分又会通过裂缝渗出。两者的耦合条件为裂缝面处的水力梯度(或饱和度)相同，即裂缝面处满足

式中：scr和sma分别为裂缝面处裂缝与混凝土的饱和度。

图3 混凝土和裂缝内的饱和度特征曲线Fig.3 Saturation characteristic curves of matrix and crack

图4 混凝土和裂缝内的渗透率特征曲线Fig.4 Permeabilities of saturated matrix and crack

3 氯离子在开裂混凝土内的输运规律

非饱和状态下氯离子在裂缝与混凝土内的输运方式主要为对流与扩散，两者的主要区别在于扩散系数不同，且胶凝材料对氯离子存在一定的结合效应。

3.1 氯离子在开裂混凝土内的输运方程

干湿交替区域混凝土中孔隙并非处于完全饱和状态，氯离子在孔隙液中扩散的质量守恒方程为[19]

考虑结合效应的氯离子质量分数可表示为：

式中：wb和wf分别为结合氯离子和自由氯离子质量分数。根据已有研究结果，氯离子在混凝土内的结合有2种形式：线性结合及非线性结合。由于线性结合一般可满足计算精度要求且能简化计算，因此，本文选择线性结合规律，其方程为

其中：γ为线性结合系数，对普通混凝土，γ介于0.159[20]与 2.400[21]之间。

由于干湿交替区域混凝土内部孔隙饱和度分布由表及里始终处于非均匀状态，从而形成孔隙饱和度分布场。孔隙液在场的作用下发生渗流，于是，溶解于其中的氯离子随孔隙液在混凝土内部形成对流现象。氯离子在孔隙非饱和状态下的输运过程可以用对流扩散方程描述[22]：

式中：JCl为氯离子在混凝土内的流速(m/s)；DCl(s)为对应饱和度下氯离子在混凝土孔隙液或裂缝中的扩散系数(m2/s)。

结合氯离子的质量守恒，可以得到干燥和湿润过程中的氯离子传输方程。

干燥过程：

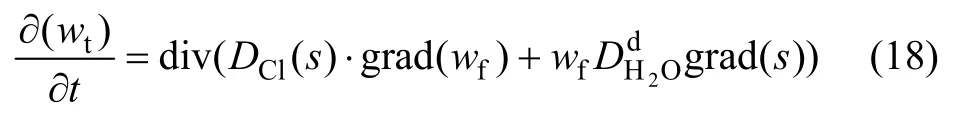
湿润过程：

3.2 氯离子在混凝土和裂缝内的扩散系数

氯离子在混凝土内的扩散系数与孔隙饱和度有关，饱和度越大，扩散系数越大，根据文献[16]，可假设非饱和状态下氯离子在混凝土内的扩散系数与饱和度成正比，则

非饱和状态下氯离子在裂缝内的扩散系数与饱和度的关系与在混凝土内类似，也呈指数关系。

其中：为饱和状态下氯离子在裂缝内的扩散系数，与裂缝宽度有关；n为幂指数。研究表明：对于宽度大于0.1 mm的裂缝，不存在溶液流动时，=Ds[23]，存在溶液流动时，= 5 0Ds[14](其中：Ds为相同条件下氯离子在溶液中的自由扩散系数)。

3.3 耦合条件

由于氯离子在裂缝和混凝土内的渗透系数不同，因此，在湿润过程中，裂缝内的部分氯离子会侵入混凝土，在整个干湿交替过程中，裂缝面处的氯离子浓度相同，即裂缝面处的氯离子浓度满足

式中：和分别为裂缝面处裂缝与混凝土内的自由氯离子质量分数。

4 数值模拟及试验验证

为了验证上述模型的准确性，设计如下试验，并根据上述输运方程对试件进行有限元分析，比较计算结果与实验结果之间的相关性。

4.1 试验设计

试验采用的素混凝土试件形式如图5所示，长×宽×高为100 mm×200 mm×1 000 mm。原材料为普通硅酸盐水泥(P.O 42.5)；河砂，最大粒径为2.5 mm；碎石，最大粒径为15 mm；普通自来水。试验采用的水灰比为 0.53，混凝土中各材料用料为：水泥 412 kg/m3，水 220 kg/m3，砂 641 kg/m3，石子 1 046 kg/m3。

图5 试验试件示意图(单位：mm)Fig.5 Schematic of test specimen

在浇筑混凝土时按指定位置插入0.2 mm厚的不锈钢片。插入深度为40 mm，间距为150 mm。浇筑2 h后将不锈钢片拔出，并将试件放入(20±3) ℃的水中养护28 d，然后将其余5个表面用防腐涂料处理，测量实际裂缝宽度，最后将试件放入8%的NaCl溶液中经受周期为14 d的干湿循环，其中干燥和湿润时间相等，首尾相连。暴露160 d后取出，待表面干燥后在暴露表面沿裂缝面及距离裂缝15 mm和30 mm截面处用直径为6 mm的钻头取样，沿深度每5 mm取1个粉样，取至40 mm，相同截面每一深度取6个位置的粉样混合，然后将粉样在(100±5) ℃的烘箱中烘2 h，并用孔径为0.63 mm的筛子筛除较大颗粒后取出1.5 g用10 mL去离子水萃取，摇匀后静置24 h，用标定过的RCT电极测试其中电位，并转化为相应的自由氯离子质量分数。试验同时放置3块相同配合比的立方体试件，并使其始终处于饱和状态，浸泡160 d后取出对同一组试样分别采用蒸馏水和萃取液萃取后测试，得到氯离子结合系数。并对不同深度的自由氯离子质量分数进行拟合，得到饱和状态下的表观氯离子扩散系数和表面氯离子质量分数，如表1所示。

表1 有限元模拟参数Table 1 Values of parameters used in numerical simulation

4.2 有限元模型及参数

由于上述水分和氯离子传输模型均为偏微分方程，且无法求出其解析解，因此，本研究采用可求解偏微分方程的有限元软件COMSOL Multiphisics进行计算。根据试验对象，取出带有裂缝的80 mm×50 mm的二维平面模型，如图6所示，模型中下部有1条平均宽度为0.32 mm和深度为40 mm的直线型裂缝。模型所采用的参数如表1所示。由于溶液不可避免地存在流动，因此，取饱和状态下氯离子在裂缝内的扩散系数为 50倍的Ds，根据文献[24]，取Ds=1.5×10-9m2/s[14]。干湿循环的一个循环周期为14 d，干燥和湿润过程时间相等，且首尾相连。由于氯离子在裂缝与混凝土内的扩散始终与饱和度有关，因此，设计2个物理场：一个为描述水分运动的扩散场，另一个为描述氯离子迁移的对流-扩散场，其中后者采用系数型的PDE方程。2个物理场之间通过孔隙(裂隙)饱和度相互联系。有限元模型如图7所示。采用三角形单元，共3 177个，其中裂缝内及靠近裂缝的单元尺寸较小，远离裂缝的单元尺寸较大，试算结果稳定。

图6 氯离子在开裂混凝土内计算模型(单位：mm)Fig.6 Simulation model of chloride ingress in cracked concrete

图7 氯离子在开裂混凝土内计算有限元网格Fig.7 Finite element meshes for numerical simulation of chloride ingression into cracked concrete

4.3 边界条件

对水分渗透模型，湿润时表面饱和度始终为100%；由于干燥时水分在混凝土表面蒸发速度很快，因此假定干燥过程中，模型表面孔隙饱和度与环境相对湿度相对应，为50%。

对氯离子侵入模型，湿润时类似于长期浸泡现象，采用Dirichlet边界条件，根据对饱和状态下的拟合结果取表面氯离子质量分数为0.6%；干燥时，氯离子不随水分蒸发，保留在混凝土表层，可用偏微分方程的Neumann边界条件表示，即表面氯离子浓度梯度为0，假设氯离子入侵方向为y，则有 dw/ dy= 0 ，表示孔隙液内氯离子质量分数为

4.4 计算与试验结果

利用上述给定参数及边界条件对模型进行有限元分析，计算得到的结果与试验结果如图8所示。由图8可见：干湿交替作用下得到的Cl离子质量分数要大于饱和状态下得到的Cl离子质量分数，干湿循环产生的氯离子累积效应使得氯离子质量分数在距离表面 5 mm左右出现1个峰值；在同一深度下，距离裂缝15 mm处混凝土中的氯离子质量分数大于距离裂缝 30 mm处的质量分数，即距离裂缝越近，氯离子质量分数越大，这说明裂缝对氯离子的侵蚀有重要影响。由图8可看出：除表层数据(0～5 mm)有较大误差外(这可能是因为表层的氯离子侵蚀机理较复杂)，其他位置的氯离子质量分数计算值与试验值较符合。这说明该模型可以用于计算海水干湿交替下氯离子在开裂混凝土内的传输。

图8 距离裂缝不同位置氯离子的计算值与试验值比较Fig.8 Comparison between calculated chloride profiles and test values in concrete near crack

5 参数敏感性分析

与氯离子在饱和混凝土内的扩散相比，非饱和状态下开裂混凝土中的氯离子输运模型增加了4个重要参数：裂缝宽度、深度、循环周期和初始饱和度。本文根据上述有限元模型对这些参数的影响进行研究，其中裂缝深度分别为20，30和40 mm，平均宽度分别为0.1，0.2和0.3 mm，每周期分别为8，14和20 d，初始饱和度为100%，75%和50%。侵蚀时间为160 d，表面氯离子质量浓度为13 g/m3，混凝土和裂缝内的氯离子扩散系数分别为 1.0×10-11m2/s和 7.5×10-8m2/s。计算得到的裂缝内和裂缝附近混凝土(距离裂缝5 mm)内的氯离子质量分数如图9所示。

由图 9(a)可看出：裂缝内的氯离子质量分数远大于混凝土内的氯离子质量分数；超出裂缝后，氯离子质量分数迅速减小。因此，裂缝深度越大，超出裂缝部分的氯离子质量分数越大。

图9 裂缝深度、宽度、干湿环境周期、初始饱和度对自由氯离子质量分数的影响Fig.9 Effects of crack depth, width, cycle time and initial saturation on free chloride concentration in crack and concrete

由图9(b)可见：当裂缝宽度从0.1 mm增大到0.3 mm时，氯离子质量分数几乎没有变化。可见：当裂缝宽度超过一定值后，裂缝宽度对裂缝内和混凝土内的氯离子传输影响较小。

循环周期时间对氯离子侵蚀的影响如图 9(c)所示。由于对流效应在干燥和湿润初期比较明显(此时饱和度变化比较大)，因此，每一循环周期越小，相同时间内的对流次数越多，导致混凝土和裂缝内的氯离子质量分数越大。

混凝土内初始饱和度对裂缝中的氯离子质量分数也有一定程度的影响，如图9(d)所示。除浅层外，初始饱和度越小，相同深度内裂缝中的氯离子质量分数越大，而混凝土中的氯离子质量分数越小，但均不明显。这是因为水分在裂缝中的传输速度远大于在混凝土内的传输速度，氯离子在裂缝内的传输方式以对流为主，在混凝土内以扩散为主(尤其是一定深度内)，初始饱和度越小，对流现象越明显，但同时也使混凝土内的氯离子扩散系数减小，从而增大了裂缝内的氯离子质量分数，而减小了混凝土内的氯离子质量分数。

6 结论

(1) 在相同侵蚀时间内，对比同一深度的氯离子，干湿循环下得到的质量分数要大于饱和状态下得到的质量分数。

(2) 在干湿交替作用下，除表层外，裂缝内部的氯离子质量分数要大于混凝土内的氯离子质量分数，且距离裂缝越远，同一深度内的氯离子质量分数越小。

(3) 0.1 mm以上的裂缝宽度对裂缝和混凝土内的氯离子质量分数影响很小；裂缝深度对超出裂缝部分区域的氯离子质量分数影响较大。

(4) 干湿循环周期时间越短，裂缝和混凝土内的氯离子质量分数越大，但不明显。

(5) 混凝土内初始饱和度对深层氯离子质量分数有微弱的影响，裂缝内的氯离子质量分数随初始饱和度增大而增大，而混凝土内氯离子质量分数变化规律正好相反。

(6) 本文提出的模型及模拟结果可为海水干湿交替作用下混凝土结构的耐久性设计提供参考。

[1] 金伟良, 金立兵, 延永东, 等. 海水干湿交替区氯离子对混凝土侵入作用的现场检测和分析[J]. 水利学报, 2009, 40(3):364-371.

JIN Weiliang, JIN Libing, YAN Yong-ong, et al. Field inspection on chloride ion-intrusion effect of seawater in dry-wet cycling zone of concrete structures[J]. Journal of Hydraulic Engineering, 2009, 40(3): 364-371.

[2] 姬永生, 袁迎曙. 干湿循环作用下氯离子在混凝土中的侵蚀过程分析[J]. 工业建筑, 2006, 36(12): 16-23.

JI Yongsheng, YUAN Yingshu. Transport process of chloride in concrete under wet and dry cycles[J]. Industrial Construction,2006, 36(12): 16-23.

[3] 王铁梦. 工程结构裂缝控制[M]. 北京: 中国建筑工业出版社,1997: 1-5.

WANG Tiemeng. Control of cracking in engineering structure[M]. Beijing: China Architecture & Building Press,1997: 1-5.

[4] Wittmann F H, Beltzung F, Zhao T J. Shrinkage mechanisms,crack formation and service life of reinforced concrete structures[J]. International Journal of Structural Engineering,2009, 1(1): 13-28.

[5] Warren T E, Root P J. The behaviour of naturally fractured reservoirs[J]. Soc Pet Eng J, 1963(3): 245-255.

[6] 周志芳. 裂隙双重介质地下水运动参数反演分析[J]. 水动力学研究与进展, 2003, 18(6): 742-747.

ZHOU Zhifang. Inverse analysis of parameters for groundwater movement in fissured double media[J]. Journal of Hydrodynamics, 2003, 18(6): 742-747.

[7] 同登科, 张鸿庆, 王瑞和. 非线性双重介质模型的精确解及动态特征[J]. 应用数学和力学, 2005, 26(10): 1161-1167.

TONG Dengke, ZHANG Hongqing, WANG Ruihe. Exact solution and Its behavior characteristic of the nonlinear dual-porosity model[J]. Applied Mathematics and Mechanics,2005, 26(10): 1161-1167.

[8] Pel L, Kopinga K, Brocken H. Moisture transport in porous building materials[J]. Heron, 1996, 41(2): 95-105.

[9] Hall C. Water sorptivity of mortars and concretes: A review[J].Magazine of Concrete Research, 1989(41): 51-61.

[10] Wong S F, Wee T H, Swaddiwudhipong S, et al. Study of water movement in concrete[J]. Magazine of Concrete Research, 2001,53(3): 205-220.

[11] Samson E, Marchand J, Snyder K A, et al. Modeling ion and fluid transport in unsaturated cement systems in isothermal conditions[J]. Cement and Concrete Research, 2005, 35(1):141-153.

[12] Reinhardt H E. Penetration and permeability of concrete-barriers to organic and contaminating liquids: RILEM Report 16[M].New York: Taylor & Francis, 1997: 123-153.

[13] Koichi Maekawa, Rajesh Chaube, Toshiharu Kishi. Modeling of concrete performance[M]. E & FN Spon, London, 1999.

[14] ISHIDA T, IQBAL PON, ANH H T L. Modeling of chloride diffusivity coupled with non-linear binding capacity in sound and cracked concrete[J]. Cement and Concrete Research, 2009,39(10): 913-923.

[15] 金伟良, 张奕, 卢振勇. 非饱和状态下氯离子在混凝土中的渗透机理及计算模型[J]. 硅酸盐学报, 2008, 36(10):1362-1369.

JIN Weiliang, ZHANG Yi, LU Zhenyong. Mechanism and mathematic modeling of chloride permeation in concrete under unsaturated state[J]. Journal of the Chinese Ceramic Society,2008, 36(10): 1362-1369.

[16] Chaube R P, Shimomura T, Maekawa K. Multiphase water movement in concrete as a multi-component system[C]//Proceedings of the 5th RILEM International Symposium on Creep and Shrinkage in Concrete. Barcelona, E&FN Spon,London, 1993: 139-144.

[17] Corless R M, Gonnet G H, Hare D E G, et al. On the Lambert W function[J]. Advances in Computational Mathematics, 1996(5):329-359.

[18] Boulfiza M, Sakai K, Banthia N, et al. Prediction of chloride ions ingress in uncracked and cracked concrete[J]. ACI Materials Journal, 2003, 100(1): 38-48

[19] Saetta A V, Scotta R V, Vitaliani R V. Analysis of chloride diffusion into partially saturated concrete[J]. ACI Materials Journal, 1993, 90(5): 441-451.

[20] Mohammed T U, Hamada H. Relationship between free chloride and total chloride contents in concrete[J]. Cement and Concrete Research, 2003, 33(9): 1487-1490.

[21] LU Xinying, LI Cuiling, ZHANG Haixia. Relationship between the free and total chloride diffusivity in concrete[J]. Cement and Concrete Research, 2002, 32(2): 323-326.

[22] 林刚, 刘应华. 干湿交替下混凝土氯离子运输模拟[J]. 武汉工业学院学报, 2009, 28(3): 68-71.

LIN Gang, LIU Yinghua. Modeling chloride penetration into concrete under drying-wetting cycles[J]. Journal of Wuhan Polytechnic University, 2009, 28(3): 68-71.

[23] Djerbi A, Bonnet S, Khelidj A, Baroghel-bouny. Influence of traversing crack on chloride diffusion into concrete[J]. Cement and Concrete Research, 2008, 38(6): 877-883.

[24] Mills R, Lobo V M M. Self-diffusion in electrolyte solutions: a critical examination of data compiled from the literature[M].Amsterdam: Elsevier, 1989: 95-153.