Al-Zr,Al-Y和Zr-Y二元合金熔体热力学性质的计算
2013-09-12李红英鲁晓超宾杰魏冬冬曾翠婷高兆和
李红英,鲁晓超,宾杰,魏冬冬,曾翠婷,高兆和
(中南大学 材料科学与工程学院,湖南 长沙,410083)
铝及铝合金具有比强度高、塑韧性较好和可加工性能好等优点,广泛应用于建筑、航天航空、汽车和电力传输等众多领域。随着科学技术的不断发展,对铝及铝合金的性能提出了更高的要求,必须开发新型高性能铝合金、提升传统铝合金的综合性能来满足应用需求[1]。微合金化是改善传统铝合金组织性能和开发新型高性能铝合金的有效手段,向铝中添加适量Zr等过渡族元素,能够起到细化晶粒的作用,有效提高合金的韧性和强度,达到改善合金的耐热性、抗蠕变性及耐腐蚀性的目的[2]。在铝中添加少量Y等稀土元素,够起到净化铝合金熔体和细化晶粒的作用,从而改善机械性能和耐腐蚀性,提高铝合金的高温性能[3-5]。微合金化及合金设计的基础是合金体系的热力学性质,然而,测定合金体系的热力学性质的高温实验难度大,而且实验准确性也低。为了计算合金体系热力学性质,de Boer等[6]提出了计算生成焓的模型,对于计算二元合金的热力学性质有较高的准确性。国内外研究人员运用Miedema模型进行了大量计算,其中关于Al-Er和Si-Er二元合金的热力学性质计算[7]、贵金属与铝二元合金生成焓的计算[8]、Zn-Mn和Zn-Ti二元合金的热力学性质计算[9]都取得了较理想的效果,但是,未见利用Miedema模型对Al-Zr,Al-Y和Zr-Y二元系进行热力学性质计算的报道。本研究利用Miedema模型,基于合金元素的基本性质及Al-Zr和Al-Y二元合金相图,根据热力学基本原理分别计算Al-Zr,Al-Y和Zr-Y二元系统的混合焓、过剩熵、过剩吉布斯自由能以及各组元的活度,并把部分结果和实验结果进行对比,确定Al3Zr和Al3Y相的析出顺序。
1 模型的建立
1.1 Miedema混合焓模型
Miedema模型是一个半经验模型,从二元合金系的大原子图像出发,把Wigner-Seitz运用于纯金属的元胞模型推广到计算二元合金的混合焓,摩尔分数分别为xA和xB的A-B二元合金,其混合焓ΔHmix可用下式计算:
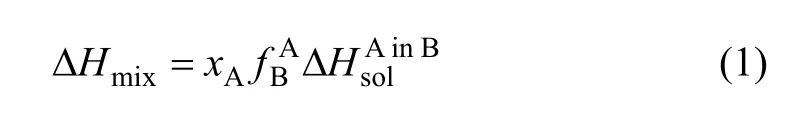

式中:Va为纯组元A的原子摩尔体积;和分别为组元A和B的电负性参数;(nws)A和(nws)B分别为组元A和B的Wigner-seitz元胞边界的电子密度平均值;a,q,R和p为经验参数,-R/p为过渡族和非过渡族元素形成二元合金时的修正项;一般情况下取q/p=9.4,参数a根据元素原子价取不同的值,对于单价或碱金属,a=0.14,对于双价金属,a=0.1,对于三价金属以及 Cu,Ag和 Au,a=0.07,对其他金属,a=0.04;和分别为A和B原子的表面浓度,
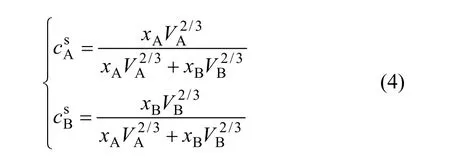
式中:VA和VB分别为纯组元A和B在形成合金后的原子摩尔体积,
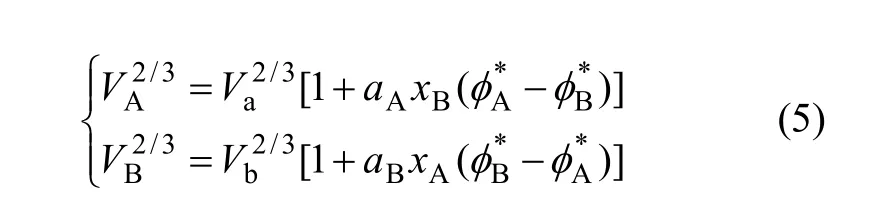
式中:Va和Vb分别表示纯组元A和B的原子摩尔体积。
将式(2)~(5)代入式(1),针对有序合金和无序合金分别得到式(6)和式(7),可用于计算二元合金的混合焓。
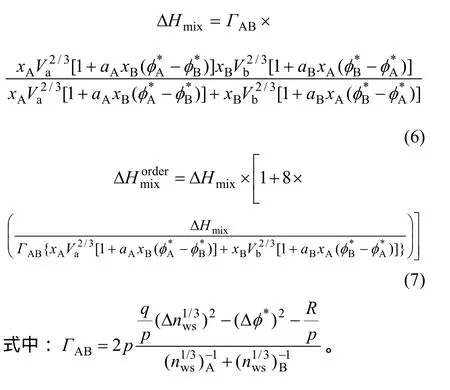
1.2 组元活度及活度系数的计算
在二元合金体系中,体系的过剩吉布斯自由能和过剩熵、混合焓 ΔH之间的关系可用式mix(8)表达,Tanaka和Gokcen在自由体积理论的基础上建立了与ΔHmix之间的关系[10],如式(9)所示。
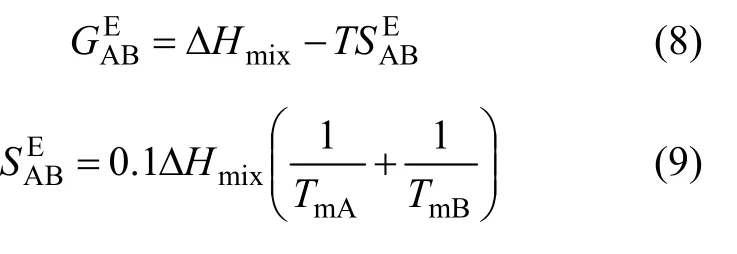
式中:T为体系的绝对温度(K);TmA和TmB分别为组元A和B的熔点。
由式(8)和式(9)可得:
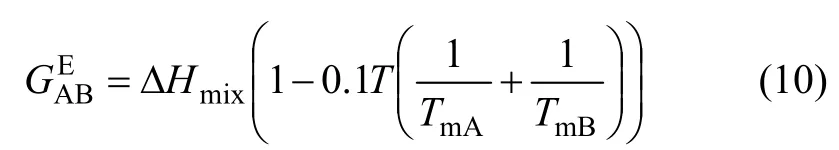
偏摩尔过剩吉布斯和可分别用式(11)和(12)计算。
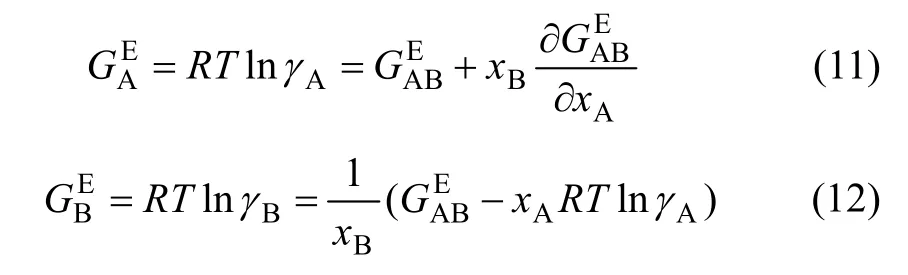
各组元的活度则为

式中:n为A或B;γA和γB分别为组元A和B的活度系数,可分别用式(14)和(15)求得:
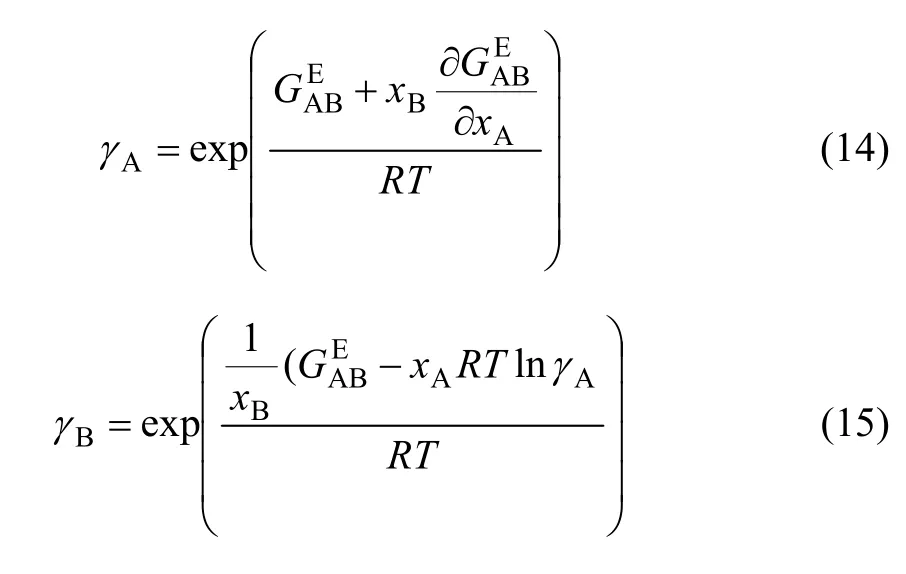
1.3 二元合金熔体反应的吉布斯自由能变化
在A-B二元相图中,成分为xi的A-B二元合金体系的温度降为Ti时,开始从液相中析出 AmBn相,发生反应mA+nB=AmBn(s),该反应的标准吉布斯自由能变化可用式(16)计算[11]。
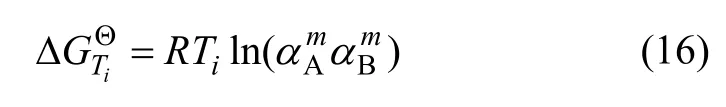
式中:αA和αB分别为组元A和B的活度,可以由式(13)计算得到。
通过式(16),可以计算不同ci(Ti)下的 Δ,利用Origin软件拟合出 Δ和Ti的关系式:

其中:a和b为拟合常数。
1.4 计算采用的参数
计算采用的基本参数来源于文献[12],表 1所示为拟计算合金元素的参数值。
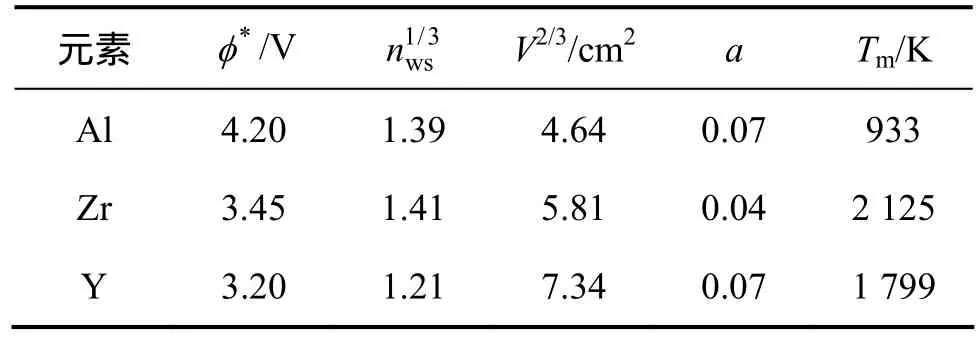
表1 Al,Zr及Y的基本参数Table 1 Parameters of Al, Zr and Y
2 计算结果及分析
2.1 Al-Zr二元合金
图1所示为Al-Zr二元合金体系的混合焓、过剩熵、过剩吉布斯自由能以及各组元的活度计算结果,对于任意浓度,Al-Zr二元合金熔体的混合焓、过剩熵和过剩吉布斯自由能都小于0。计算结果表明:Al和Zr原子之间存在很强的相互作用,这与Al和Zr原子的电子密度、电负性和原子体积等基本性质相差较大的事实相符。从图1(a)可以看出:采用Miedema模型计算的混合焓与 Saunders等的实测结果[13-15]基本吻合,但是,由于Miedema模型忽略了温度的影响,所以计算结果存在一定误差。从图1(b)可以看出:过剩熵SE的绝对值较小,在实际运用时可以忽略,直接取SE=0。根据Al-Zr二元合金相图[16],Al和Zr可以形成多种金属间化合物,而Al3Zr,Al2Zr,Al3Zr2,AlZr,Al4Zr3,Al2Zr5,Al3Zr5,AlZr2和 AlZr3等有序相存在,导致液相中各组元活度相对于理想溶液产生负偏差,从图1(d)可以看出:Al和Zr的活度相对于理想溶液存在着较大的负偏差,表明采用 Miedema模型计算Al-Zr二元合金熔体各组元的活度结果有较大的可信度。
从Al-Zr二元相图上选取1 623~1 853 K间的6个温度点以及对应成分,计算Al3Zr相析出反应的吉布斯自由能,计算结果如图2所示。
利用Origin软件对 Δ与Ti进行线性拟合,得到Al3Zr析出反应的 ΔGΘ与T的关系:
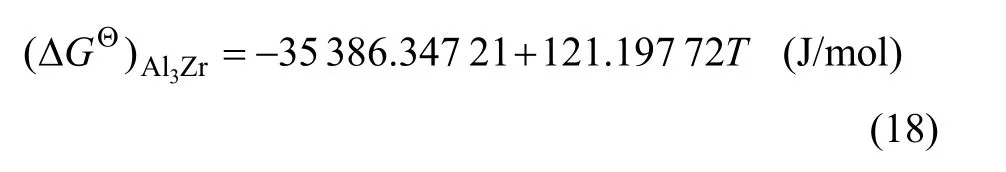
2.2 Al-Y二元合金
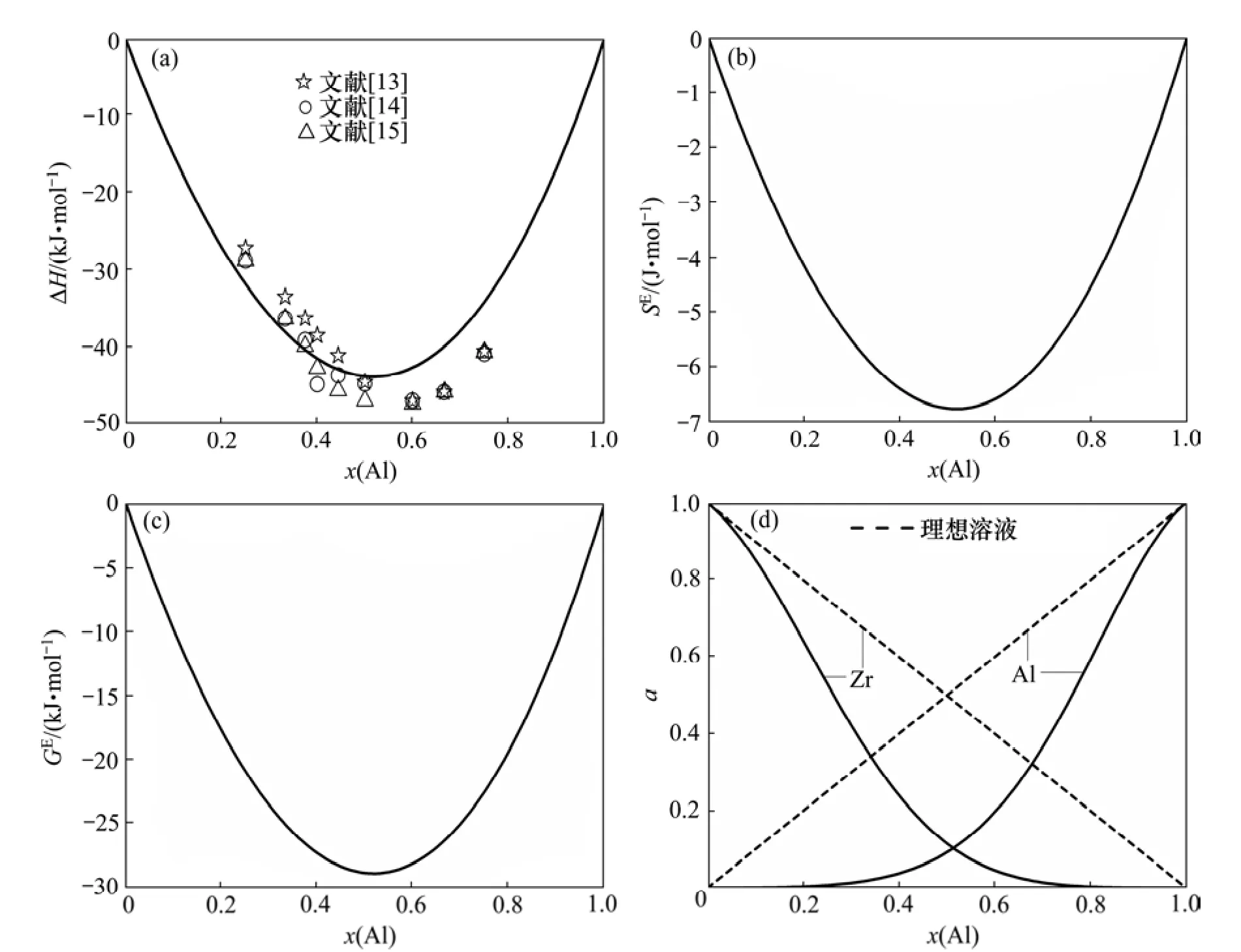
图1 在2 200 K温度下Al-Zr合金热力学数据与合金成分的关系Fig.1 Relationship of thermodynamic data and components of Al-Zr binary alloy at 2 200 K
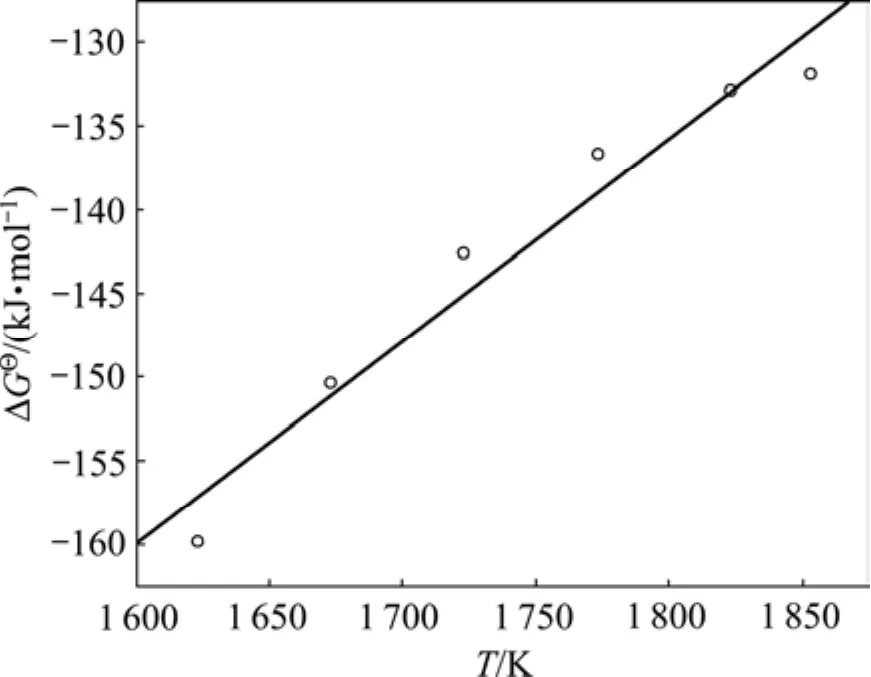
图2 Al3Zr相析出反应的 Δ G Θ 与T的关系Fig.2 Relationships of Δ G Θ and T for precipitation reaction of Al3Zr in Al-Zr binary alloy
图3所示为Al-Y二元合金体系的混合焓、过剩熵、过剩吉布斯自由能以及各组元的活度计算结果,从图3可以看出:在任意浓度,Al-Y二元合金熔体的混合焓、过剩熵和过剩吉布斯自由能也都小于0 J,与Al-Zr二元合金熔体的计算结果极为相似,但Al-Y合金的混合焓、过剩熵、过剩吉布斯自由能都比 Al-Zr合金熔体的略高。从图 3(a)可以看出:理论计算结果与Shakhshir的计算结果[17]较符合,Al-Y合金与Al-Zr合金的负偏差相似,Al-Y合金各组元的活度与Al-Zr合金各组元的活度也相似,这是由于Zr原子和Y原子的基本性质很接近,在元素周期表中Zr和Y相邻(Y的原子序数为39,Zr的原子序数为40)。从图3(d)可以看出:采用Miedema模型计算的Al-Y合金各组元的活度与Pctrusheveskii的实验活度[18]也较吻合,表明 Miedema模型适于对 Al-Y合金进行热力学计算。
从Al-Y二元相图上选取923~1 223 K间的6个温度点以及对应的液相成分,计算 Al3Y相析出反应的吉布斯自由能,计算结果如图4所示。利用Origin软件对 Δ与Ti进行线性拟合,得到Al3Y析出反应的 ΔGΘ与T的关系式:
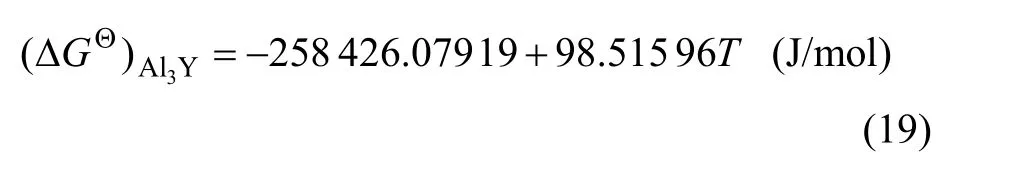
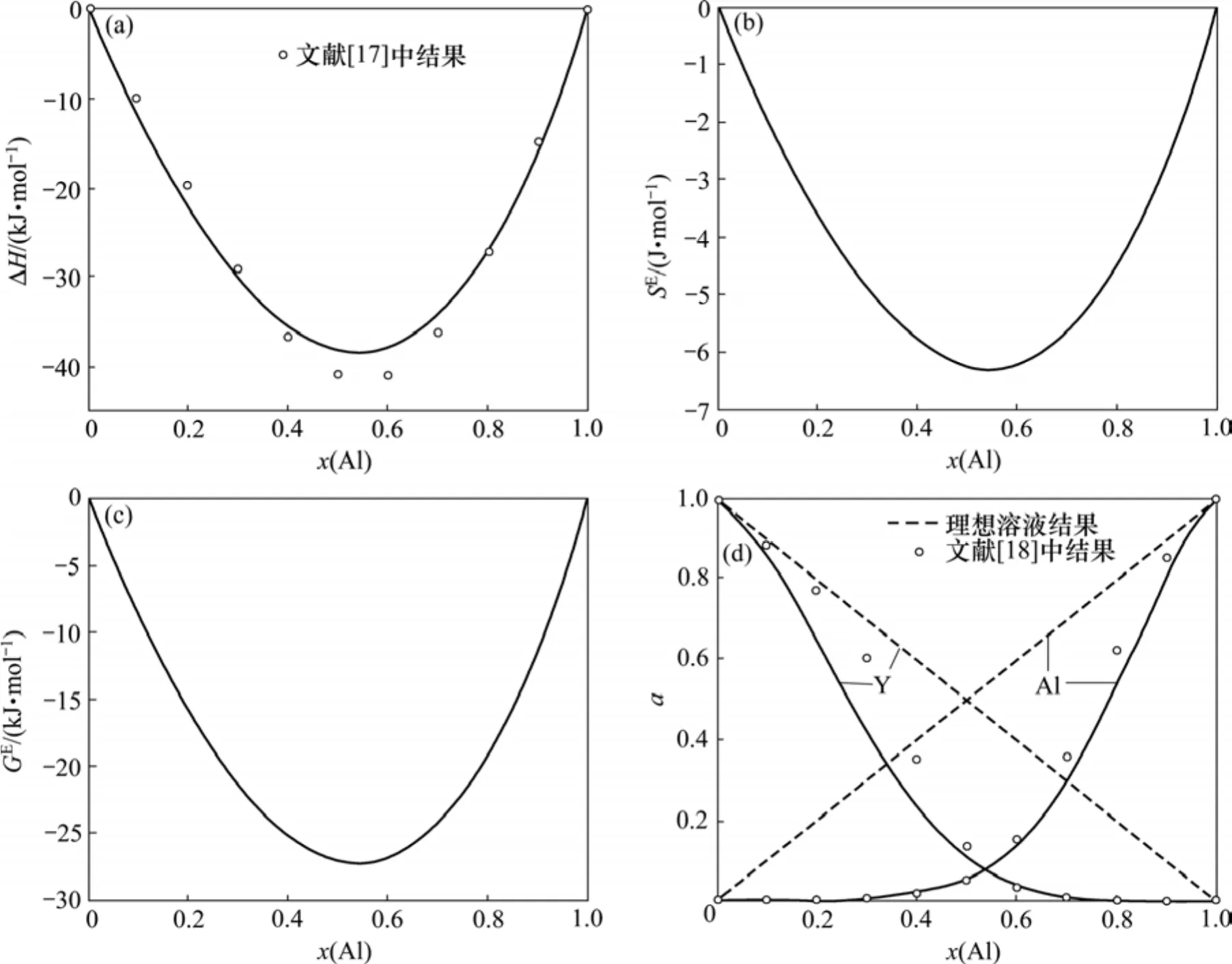
图3 在1 800 K温度下Al-Y合金热力学数据与合金成分的关系Fig.3 Relationship of thermodynamic data and components of Al-Y binary alloy at 1 800 K
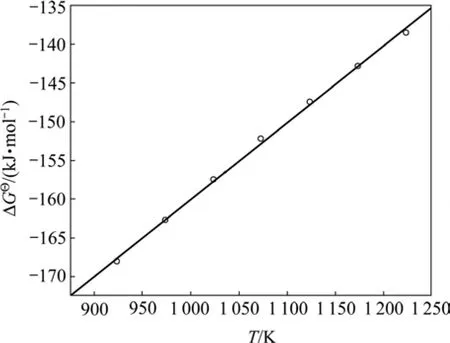
图4 Al-Y二元合金中Al3Y析出反应的 Δ G Θ 与T的关系Fig.4 Relationships of Δ G Θ and T for precipitation reaction of Al3Y in Al-Y binary alloy
2.3 Zr-Y二元合金
图5所示为Zr-Y二元合金体系的混合焓、过剩熵、过剩吉布斯自由能以及各组元的活度计算结果。从图5可以看出:在任意浓度,Zr-Y二元合金熔体的混合焓、过剩熵和过剩吉布斯自由能都大于0 J。从图5(d)可知:采用Miedema模型计算的Zr-Y合金各组元的活度与Flandorfer的实验活度[19]吻合得较好,各组元活度的计算结果相对于理想溶液存在着较大的正偏差,表明Zr原子和Y原子间的相互作用力比同类原子间的相互作用力小。根据 Zr-Y二元合金相图[16],在不同成分及温度条件下,Zr-Y合金都没有金属间化合物存在,进一步证明了上述Zr原子和Y原子的相互作用不大。


图5 在2 200 K温度下Zr-Y合金热力学数据与合金成分的关系Fig.5 Relationship of thermodynamic data and components of Zr-Y binary alloy at 2 200 K
3 结论
(1) Al-Zr和Al-Y二元合金熔体的混合焓、过剩熵、过剩吉布斯自由能都小于0 J,各组元的活度相对于理想溶液发生了较大的负偏差,而Zr-Y二元合金熔体的混合焓、过剩熵和过剩吉布斯自由能都大于0 J,各组元的活度相对于理想溶液发生了较大的正偏差,说明Al与Zr的Y原子有较强的相互作用,而Zr和Y原子相互作用不大。
(2) Miedema模型能够适用于Al-Zr,Al-Y和Zr-Y 3个二元合金熔体的热力学性质计算,在实际运用中可以直接忽略过剩熵。
(3) 计算得到Al3Zr相和Al3Y相析出的吉布斯自由能均为负值,Al3Y相析出的吉布斯自由能的绝对值更小,在纯Al中同时添加过渡族元素Zr和稀土元素Y时,Al优先与Y生成Al3Y相,过剩的Al才与Zr生成Al3Zr。
[1] 赵延阔, 李红英, 王晓峰, 等. 不同变质剂对 4032铝合金变质效果的影响[J]. 中南大学学报: 自然科学版, 2011, 42(2):361-367.
ZHAO Yankuo, LI Hongying, WANG Xiaofeng, et al. Effects of different modifiers on modification efficiency of 4032 aluminum alloy[J]. Journal of Central South University: Science and Technology, 2011, 42(2): 361-367.
[2] 李红英, 孙远, 宾杰, 等. Ce对耐热铝导体材料铸态组织和性能的影响[J]. 中南大学学报: 自然科学版, 2011, 42(10):3026-3032.
LI Hongying, SUN Yuan, BIN Jie, et al. Effect of cerium on as-cast microstructure and properties of heat-resistant aluminum conductor[J]. Journal of Central South University: Science and Technology, 2011, 42(10): 3026-3032.
[3] SHE Jia, ZHAN Yongzhong, HU Zhao-hua, et al. Experimental study of Al-Zr-Y system phase equilibria at 773 K[J]. Journal of Alloys and Compounds, 2010, 497(1/2): 118-120.
[4] LÜ Yizhen, WANG Qudong, ZENG Xiaoqin, et al. Effects of rare earths on the microstructure, properties and fracture behavior of Mg-Al alloys[J]. Materials Science and Engineering A, 2000, 278(1/2): 66-76.
[5] 李慧中, 张新明, 陈明安, 等. 钇对 2519铝合金铸态组织的影响[J]. 中南大学学报: 自然科学版, 2005, 36(4): 545-549.
LI Huizhong, ZHANG Xinming, CHEN Mingan, et al. Effect of yttrium on as-cast microstructure of 2519 aluminum alloy[J].Journal of Central South University: Science and Technology,2005, 36(4): 545-549.
[6] de Boer F R, Boom R, Mattens W C M, et al. Cohesion in metals:Transition Metal Alloy[M]. Amsterdam: Elsevier, 1988: 758.
[7] 孙顺平, 易丹青, 陈莹, 等. Al-Er和Si-Er二元合金的热力学性质[J]. 中国有色金属学报, 2009, 19(9): 1580-1586.
SUN Shunping, YI Danqing, CHEN Ying, et al. Thermodynamic properties of binary alloys of Al-Er and Si-Er[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(9): 1580-1586.
[8] 欧阳义芳, 廖树帜, 张邦维, 等. 贵金属与铝二元合金的形成热[J]. 稀有金属材料与工程, 1998, 27(3): 19-22.
OUYANG Yifang, LIAO Shuzhi, ZHANG Bangwei, et al.Formation enthalpies of noble metal-aluminum binary alloys[J].Rare Metal Materials and Engineering, 1998, 27(3): 19-22.
[9] 路贵民, 乐启炽, 崔建忠. Zn-Mn和Zn-Ti二元合金热力学性质[J]. 中国有色金属学报, 2001, 11(1): 95-98.
LU Guimin, LE Qichi, CUI Jianzhong. Thermodynamic properties of binary alloys of Zn-Mn and Zn-Ti[J]. The Chinese Journal of Nonferrous Metals, 2001, 11(1): 95-98.
[10] Tanaka T, Gokcen N, Morita Z. Relationship between enthalpy of mixing and excess entropy in liquid binary alloys[J].Zeitschrift für Metallkunde, 1990, 81(1): 49-54.
[11] 吴玉锋, 杜文博, 聂祚仁, 等. Mg-Al-M 合金中 Al-M 相(M=Sr,Nd)析出行为的热力学分析[J]. 金属学报, 2006, 42(5):487-491.
WU Yufeng, DU Wenbo, NIE Zuoren, et al. Thermodynamic analysis of the precipitation behaviors of Al-M(M=Sr, Nd)phases in Mg-Al-M alloys[J]. Acta Metallurgica Sinica, 2005,42(5): 487-491.
[12] Niessen A K, de Boer F R, Boom R, et al. Model predictions for the enthalpy of formation of transition metal alloys Ⅱ[J].Calphad, 1983, 7(1): 51-70.
[13] Saunders N, Rivlin V G. Thermodynamic characterization of Al-Cr, Al-Zr and Al-Cr-Zr alloy systems[J]. Materials Science and Technology, 1986, 2(6): 520-527.
[14] Kematick R J, Franzen H F. Thermodynamic study of the zirconium-aluminum system[J]. Journal of Solid State Chemistry,1984, 54(2): 226-234.
[15] WANG Tao, JIN Zhan-peng, ZHAO Ji-cheng. Thermodynamic assessment of the Al-Zr binary system[J]. Journal of Phase Equilibria and Diffusion, 2001, 22(5): 544-551.
[16] Baker H, Okamoto H. Alloy phase diagrams[M]. Ohio: ASM International, 1992: 501.
[17] Al Shakhshir S, Medraj M. Computational thermodynamic model for the Mg-Al-Y system[J]. Journal of Phase Equilibria and Diffusion, 2006, 27(3): 231-244.
[18] Petrusheveskii M S, Ryss G M. Calculations of the activities of components in liquid binary alloys of yttrium with aluminum and silicon[J]. Zhurnal Fizicheskoi Khimii, 1986, 60(6):1532-1535.
[19] Flandorfer H, Gröner J, Stamou A, et al. Experimental investigation and thermodynamic calculation of the ternary system Mn-Y-Zr[J]. Zeitschrift für Metallkunde, 1997, 88(7):529-538.
