一种新型回转式弹仓轨道参数化设计
2013-09-12冯保忠孙大伟李永恒
冯保忠,王 斌,孙大伟,李永恒
(西北机电工程研究所,陕西 咸阳 712099)
近年来,国内外最新研制或者装备的大口径火炮系统中,弹药输送的快速性及自动化程度越来越高[1-2]。这些火炮中的弹仓往往采用回转式结构,例如:韩国的K9弹药输送车、美国“十字军骑士”火炮系统及德国DONAR火炮系统都采用了回转式弹仓。回转式弹仓具有结构紧凑,适应性强,控制简单,取弹速度高的优点。
为了适应现代火炮发展,设计了一种新型回转式弹仓,其传动与链条传动相似,弹筒铰接组成弹链,弹链支撑在底座上,底座内设计了一条轨道,这条轨道限制弹筒沿着轨道运动,增强了传动可靠性,保证了弹链有效回转,减小弹筒的跳动。所以轨道的设计优劣决定了整个弹链周向运动的平稳与否,但轨道最初的设计采用几何方法绘制所得,缺少理论依据不理想。
1 回转式弹仓结构
回转式弹仓一般由储弹筒部件、连接部件、底座部件和驱动部件组成。如图1所示,弹丸固定在储弹筒组件内,相邻的两个储弹筒组件通过连接部件两两铰接在一起,组成闭合的回转弹链。整条弹链支撑在底座部件上,底座部件由内外两部分导轨组成,形成回转轨道,每个储弹筒底部伸出转轴,转轴限制在回转轨道内。处在弹链中部的驱动部件通过拨动储弹筒组件底部的转轴,进而带动整个弹链进行回转运动,当储弹筒转至轨道取弹位置时,就可以由其他机构将弹丸取出。某回转弹仓回转轨道中心线形状为长“O”形,如图2所示。

图1 弹仓结构
整个回转轨道可以分成4部分,2段直线和2段曲线,2段曲线和2段直线都是对称的。曲线段轨道在最初设计时采用描点的方法绘制,发现近似为椭圆曲线,后用椭圆取代,但该方法所选点数有限不够全面,缺乏理论根据。而曲线段轨道起到协调两侧直线段上储弹筒运动的重要作用,准确的曲线轨道才能保证储弹筒在直线段的速度相同,有效协调两侧储弹筒的运动,否则就会引起储弹筒运动不协调。由文献[3]中可知链传动过程中,链条运动不协调会造成链节跳动,如果弹链跳动会使得储弹筒定位不准。本文通过理论分析精确求解得到曲线段隐函数方程,并通过运动仿真验证求解所得方程曲线较椭圆曲线更加理想。
2 回转轨道中心线求解
回转轨道由2条平行直线及2条U形线相连形成如图所示轨迹曲线,A代表第n-1个储弹筒组件,B代表第n个储弹筒组件,C代表第n+1个储弹筒,AB、BC分别为相邻储弹筒间铰接连杆,A端受到驱动力的驱动使得AB运动,通过铰接点B再驱动BC运动。A点和C点运动方向相反,为了保证整条弹链运动协调,A点和C点的运动速度数值必须是相同的。由于B点限制在轨道U形区段,所以U形区域轨迹的设计影响整条弹链的可行性,整个轨道中心线的求解问题主要是U形曲线段的求解。

图2 轨道中心线
这里将问题抽象为数学模型,作如下分析。为了方便分析作如下假设:①储弹筒在竖直方向上不存在位移;②储弹筒AB、BC上的A、B、C 3点都沿轨道中心线运动,不存在脱离现象;③A、B的初始位置分别A0,B0。绘制如图所示的平面坐标系,将问题假设为:A点以V的速度向左侧前进,B点以大小为V的速度向右侧前进,C点经过的路线即所求轨迹。
A点坐标为(x1,y1)=(l-Vt,L/2),B点坐标为(x2,y2)=(Vt,-L/2),C点坐标为(x,y),满足条件

C点轨迹与V无关,令V=1带入到式(1)中,整理后得到C点轨迹的隐函数

3 轨道模型建立及仿真验证
为了验证轨道回转段是椭圆曲线还是方程曲线,首先要按照2种曲线建立轨道模型,在轨道模型基础上,运用UG/motion模块分别对2种轨道进行仿真运算。比较分析2种仿真所得结果。椭圆曲线可以利用椭圆功能直接绘制,而所求方程曲线就要用规律曲线功能。在UG中绘制规律曲线就要用到软件的参数化设计功能。
[4-5]中可知UG软件有强大参数化设计功能,可以绘制各种复杂的曲线,要实现方程曲线的绘制,必须要用到表达式功能。在创建表达式时要注意一下几点:①表达式左侧必须是一个简单变量,等式右侧是一个数学语句或一个条件语句;② 所有表达式均有一个值(实数或者整数),该值被赋给表达式的左侧变量;③ 表达式等式的右侧可认为是含有变量、数学、运算符和符号的组合和常数;④用于表达式等式右侧中的每一个变量,必须作为一个表达式名字出现在某处。
为满足表达式要求,需要将所求方程曲线参数化,这里引入变量t,经过整理得出参数化方程式
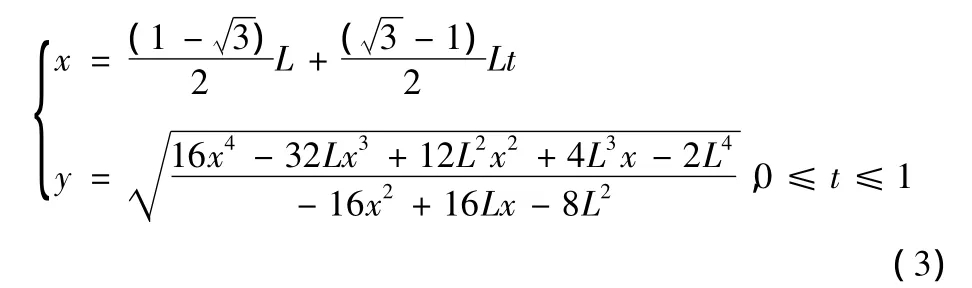
根据所得参数化方程建立轨道中心线,进而建立轨道模型如图3所示。图3中左侧轨道曲线段依据椭圆建立,右侧轨道曲线段依据方程曲线建立。为了方便分析,这里将处在曲线段的储弹筒及左右各一个储弹筒由弹链中单独取出作为研究对象,并对储弹筒组件及轨道模型进行了简化。
首先在3个储弹筒中,每相邻的2个之间建立铰接,并限制3个储弹筒沿轨道运动。分别对右侧储弹筒给予一初始速度(设定为37 mm/s)作为驱动端,使中间储弹筒沿着曲线段运动,对末端储弹进行速度检测,检测结果如图4所示。
图4中横轴为时间,纵轴为末端速度幅值,细线表示左侧模型检测结果,粗线表示右侧模型检测结果。从图表可以观察到在前期时间内,左侧模型末端储弹筒的速度值围绕37 mm/s上下浮动,而右侧模型末端储弹筒的速度恒为37 mm/s;在停止运动瞬间,左侧模型较右侧模型产生的震荡更大。由此可以得出轨道曲线段若为椭圆时会造成驱动端与末端运动不协调,而曲线段为方程曲线的轨道,驱动端和末端储弹筒速度相同运动协调。
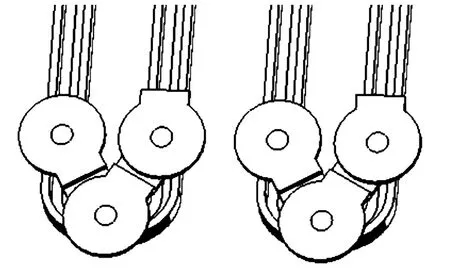
图3 仿真模型

图4 仿真结果
4 结束语
通过仿真结果不难发现,本文通过建立数学模型求解所得曲线是较为理想的曲线,该曲线能够满足设计要求。本文求解轨道曲线的方法,对同类型问题具有参考意义。随着弹药输送自动化程度的提高,回转式模块弹药仓的应用将越来越广泛,同时其轨道的设计也将受到广泛重视。
在本文中解决了储弹筒间距与两直线段轨道间距相同这种特定情况下轨道求解问题,但是随着回转式模块弹药仓的应用,必然会出现间距不同的情况,甚至异型(非长“O”形)轨道的情况,在复杂情况下弹药仓轨道的精确求解问题将是以后研究的重点。
参考文献:
[1]梁辉,马春茂,潘江峰,等.大口径火炮弹药自动装填系统研发现状和趋势[J].火炮发射与控制学报,2010(3):103-107.
[2]中国科学技术协会.2008-2009兵器科学技术学科发展报告[M].北京:中国科学技术出版社,2009.
[3]蒲良贵,纪名刚.机械设计[M].北京:高等教育出版社,2006.
[4]江洪,郦祥林,李春表,等.UG 5.0典型实例解析[M].北京:机械工业出版社,2007.
[5]胡小康.UG NX4运动分析培训教程[M].北京:清华大学出版社,2006.
