双摆头五坐标机床建模中的多解选择控制与算法验证*

尹春晖 荆怀靖 任 斐

（上海航天设备制造总厂，上海 200000）

双摆头五坐标机床建模中的多解选择控制与算法验证*

尹春晖 荆怀靖 任 斐

（上海航天设备制造总厂，上海 200000）

针对一种双摆头五坐标数控铣床，从机构学的角度论述了机床的结构模型，以坐标变换的方式建立了机床的运动模型，详细论述了机床的运动模型求解，并对其中的多解选择问题进行了探讨。在此基础上，结合五轴联动加工时，两转动轴存在的关联依赖关系，综合考虑两转动轴的加工信息，给出了一种多解选择算法。在此算法的基础上，基于VS2010平台，开发了该类机床的专用后置处理器，在VERICUT中建立了机床的仿真模型，并通过半球面以及圆框两组仿真切削试验对以上算法进行仿真验证。最后，实际加工了一个测试样件，仿真验证与实际加工的结果均表明所提出的方法正确可行。

五轴数控机床 双摆头 后置处理 多解选择

与传统三轴加工相比，五轴加工能够获得更多的加工自由度，更好的表面质量，然而，刀轴的控制和规划难度更大。五轴加工中，由于两转动轴的介入，使得在由CL数据求取NC值的反求变换过程中，产生多组解，每组解均代表一种通往指定切削位置的刀具加工路径，然而它们的效率，对工件表面质量的影响等有很大不同，错误的选择刀具路径甚至会导致刀轴出现奇异动作，致使工件报废［1］。因此，作为五轴加工的关键技术，多解选择正得到国内外学者越来越多的关注。

Sakamoto［2］将现有串联型五轴机床划分为双摆头、双转台、摆头+转台3种类型，并指出了多解选择问题的存在。唐清春［3］等和田荣鑫［4］等分别建立了A－C双转台和斜摆头+转台机床的运动学模型，并详细分析了运动学建模中的多解情况。Jung［5］等进一步提出了“以非依赖轴旋转达到极限‘反相’的数量最少”作为评价指标来解决多解选择问题。

以上类型的文献还有很多，为五轴加工技术的推广奠定了基础［6－8］。然而，这些研究更多的侧重于机床的运动学建模以及非线性误差控制，对建模后的多解选择控制等问题的关注并不是很多。同时，已提出的基于“依赖轴旋转量最小”的算法未能充分考虑两转动轴的联动依赖关系，存在一定的片面性。本文以XK2745（A－C正交双摆头）五轴机床为例，建立了机床的运动学模型，综合考虑两转动轴的加工信息，以两转动轴的权值和为转角多解的选择标准。基于VS2010，开发了该类机床的专用后置处理器，通过仿真测试与实际加工验证了该算法的正确性。

1 XK2745机床的运动学建模及求解

如图1所示，XK2745为标准正交A－C双摆头结构。A轴转动的工作范围为（－π/2，π/2），C轴转动的工作范围为（－2π，2π）。

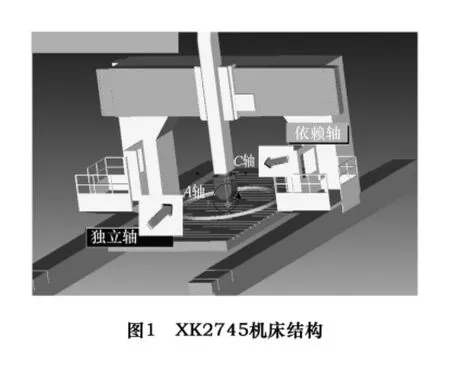
为方便进一步讨论，提取上述机床的关键要素，则机床模型可抽象为图2b，依据此图，进一步分析机床关节的运动关系，可得出其运动链结构，如图2a。

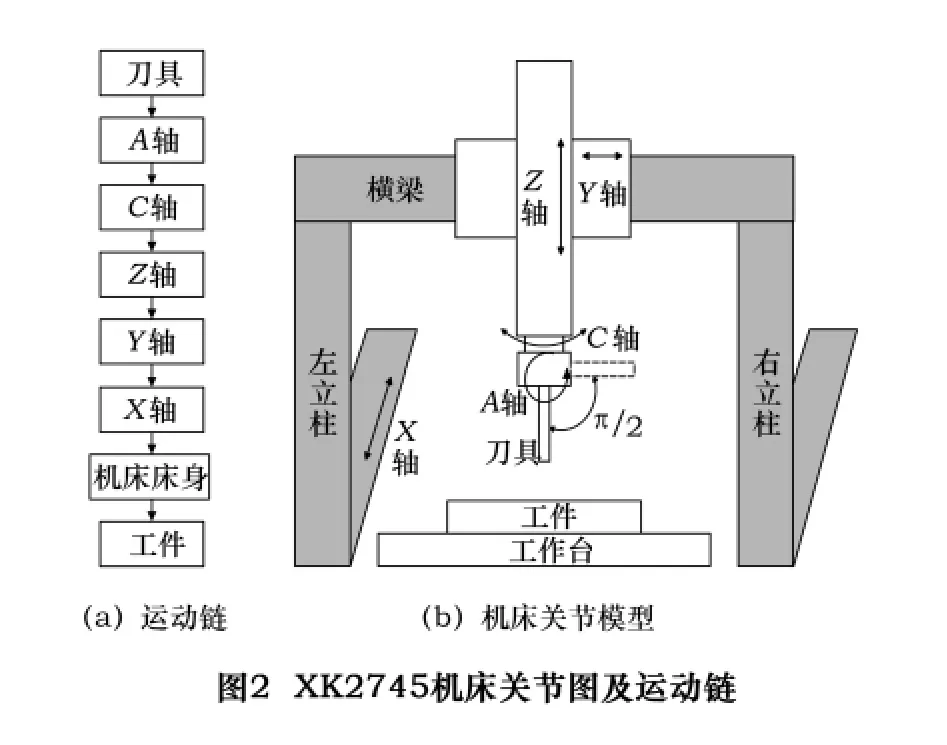
记依赖轴A的轴线平行于X轴的状态为初始状态，此时刀具轴线平行于Z轴，工件坐标系与机床坐标系方向一致，刀具坐标系与工件坐标系原点重合。机床平动轴相对于初始位置为rs（sx，sy，sz），回转轴A、C相对于初始状态的角度为θA和θC，此时工件坐标系中刀轴方向和刀轴矢量分别为u（ux，uy，uz）和rp（px，py，pz）。根据任意结构数控机床机构运动学原理，由NC数据求得CL数据的变换矩阵为

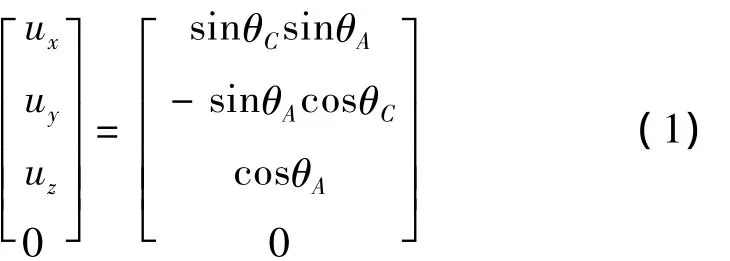
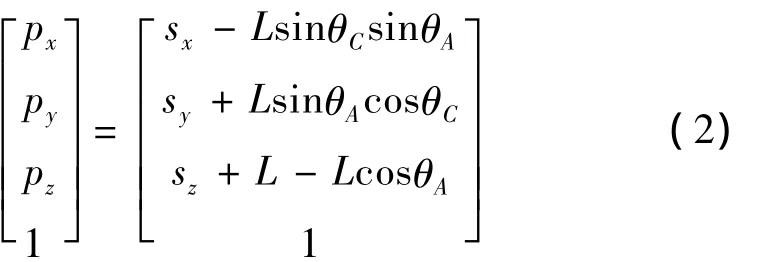
联立式（1）、（2）即可由CL数据反求出NC代码，如式（3）所示。其中 KA=±1，K=±1，0。由此可看出，联立方程组所求得的解并不唯一，若不考虑两转动轴的行程极限，一般可求出4组不同的解。

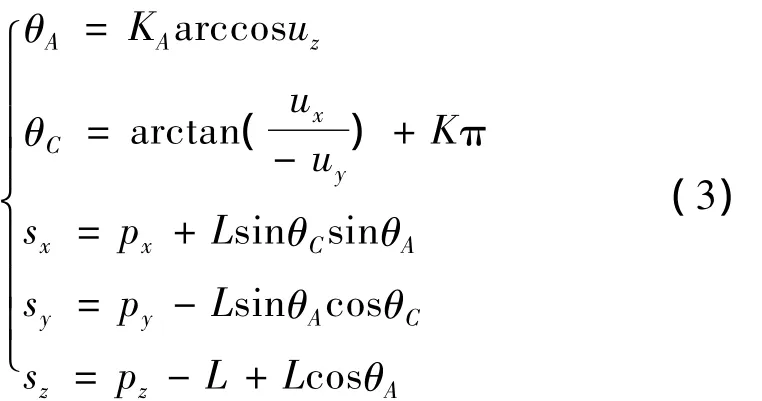
2 转角的多解分析与选择

2.1 转角的多解分析

为方便描述，下述讨论中以A代表θA，C代表θC，同时设定如下基准，令：

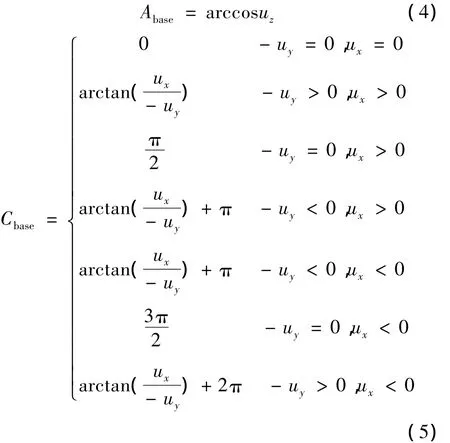
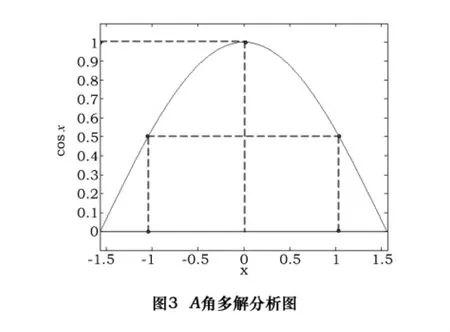
如图3所示，由于 A∈［－π/2，+π/2］，则 uz=cosA在定义域内以直线x=0对称，当且仅当uz=1时，A有唯一解，否则，对于uz的每一个值，均有两个A角与之对应。C角亦是如此。对于A角与C角的解的选择，其具体象限应按运动的连续性和各转动轴的行程范围来确定。具体讨论如下：

（1）当uz=1时，结合A角取值范围与式（1），易得：A=0，C=0。此时具有唯一解。

（2）当uz≠1时，在A轴许用工作范围内，A的取值方式为：

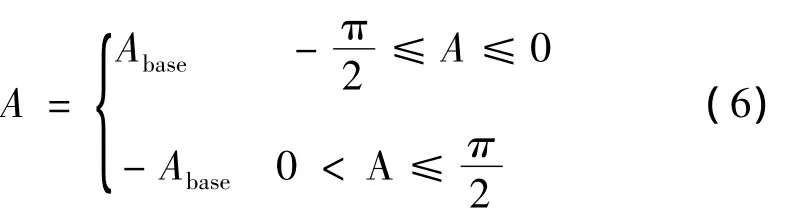
①取 A=Abase，则 sinA ＞0，由式（1）及 ux、uy的值可解得两组解。

若 －uy＞0，ux＞0。由式（1）可知，sinC ＞0，cosC＞0，C角在第一象限，对应的C角的选择方式为Cbase，又因为sinC、cosC的周期为2π且C的工作范围为［－2π，+2π］，所以 C 还可为 Cbase－2π。

同理，可得出－uy、ux其他情况下的C角。

②取 A= －Abase，则 sinA ＜0，同理，由式（1）及 ux、uy的值可解得另两组解。

整理上述结论可得：

（1）当 uz=1 时，A=0，C=0。

（2）当uz≠1时，对应的解为：

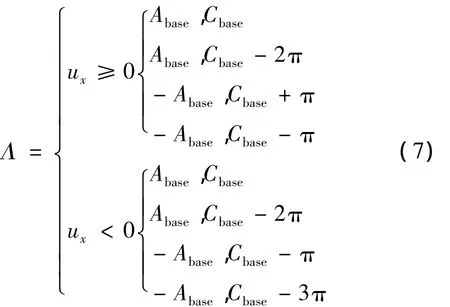
2.2 转角的多解选择

基于五轴联动加工时，两转动轴存在的关联依赖关系，综合两转动轴的加工信息并结合式（7）所得的结果，设定：

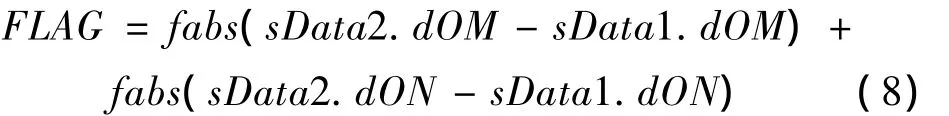
式中：sData为储存NC代码的结构体;dOX、dOY、dOZ、dOM、dON分别代表3平动轴与两转动轴的加工数据。sData1与sData2储存相邻两行NC数据，则转角多解选择标准为：使相邻两行NC代码中，对应转角差的绝对值的和最小（即式（8）中的FLAG最小）。

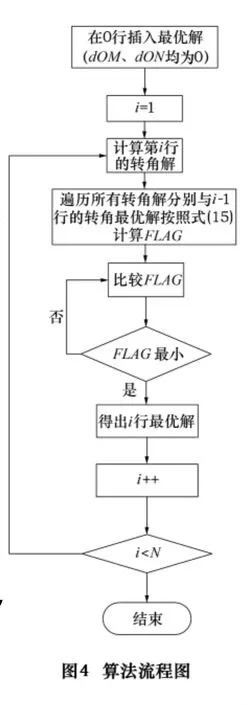
如图4所示，对于刀位文件的每一行数据，都将计算得出多组转角解，将所有转角解的组合分别与上一行选择出的最优解按照式（8）计算得出 FLAG，比较所有FLAG的大小，将最小 FLAG对应的转角组合确定为此行数据的最优解。对于首行数据，人为插入一组解（dOM=0，dON=0），视此解为0 行最优解，首行数据的多组解分别与此解进行上述处理，得出首行最优解。

3 XK2745后置处理器的实现

根据解释执行的原则，后置处理程序采用面向对象的方法开发，采用式（1）、（2）、（3）进行坐标转换部分程序设计;依据式（7），将多解选择算法添加到后置处理过程中。软件界面如图5所示。提供G代码和CL文件路径的编辑框，并利用了Windows系统内置的打开文件、关闭文件、保存文件等对话框;添加了平动轴与转动轴的偏移补偿;充分考虑了人机工程学原理，设计简单的界面和操作流程以方便使用。

4 算法验证

4.1 仿真测试

为了验证上述算法和后置处理器，在VERICUT环境下，建立XK2745机床的仿真模型。在设置好各项相关参数之后，将由上述后置处理器生成的NC代码导入到VERICUT中，进行仿真加工，见图6。

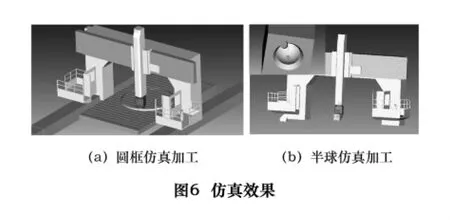
在两组仿真切削实验中，加工过程平稳，无空刀、过切、欠切现象。

4.2 机床切削加工实验

仿真通过后，在实际机床上加工了圆框实物，加工过程中，机床运行平稳，加工后的零件（见图7）各项指标符合图纸要求，从而验证了所提出算法和后置处理器的正确性。

5 结语

建立了XK2745五轴数控机床的运动学模型，对求解过程中的多解问题进行了详细的分析，并基于五轴联动加工时，两转动轴的联动依赖关系，综合两个转动轴的加工信息，给出了一种多解选择算法。开发了XK2745机床的专用后置处理器，通过在VERICUT环境下的两组仿真测试以及圆框样件的实际加工实验，验证了所提出算法和后置处理器的正确性。

［1］KNUT S.Inverse kinematics of five－axis machines near singular configurations［J］.International Journal of Machine Tools ＆ Manufacture，2007，47（2）：299 －306.

［2］Sakamoto S，Inasaki I.Analysis of generating motion for five－axis machining centers［J］.Trans.Jpn.Soc.Mech.Engr.Ser.1993，59（561）：1553－1559.

［3］唐清春，张仁斌，何俊，等.基于VB BV100五轴联动加工中心后置处理的研究［J］.机械设计与制造，2012（2）：73－75.

［4］田荣鑫，任军学，孟晓贤，等.斜摆头五坐标数控加工机床的后置处理算法研究［J］.机械设计与制造，2007（12）：117－118.

［5］Jung Y H，Lee D W，Kim J S，et al.NC post－processor for 5－axis milling machine of table － rotating/tilting type［J］.Journal of Materials Processing Technology，2002，130/131：641－646.

［6］She Chen－Hua，Chang Cheng－Chun.Development of a five－axis postprocessor system with a nutating head［J］.Journal of Materials Processing Technology，2007，187/188：60－64.

［7］O Remus Tutunea － Fatan，Hsi－ Yung Feng.Configuration analysis of five － axis machine tools using a generic kinematic model［J］.International Journal of Machine Tools＆ Manufacture，2004，44：1235－1243.

［8］Yun Jae－Deuk，Jung Yoong－Ho，Tae Dong－Been，et al.A geometric postprocessing method using joint positions of a 5－axis machine［C］.Proceeding of the World Congress on Engineering and Computer Science，San Francisco，2009.

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Multi-choice and verification of a spindle-rotating five-axis machine tool

YIN Chunhui， JING Huaijing，REN Fei
（Shanghai Spaceflight Manufacture（Group）Co.，Ltd.，Shanghai 200000，CHN）

The mechanism model of a spindle－rotating machine is proposed in this paper according to the mechanism theory.The movement model is established using coordinate transformation，and the solving of this model is discussed.Based on these and the relationship between the two rotating axis，an efficient algorithm for multi－choice has been presented.A dedicated post－processor was developed by VS2010 language.Two simulation cutting experiments of a hemisphere and a circle frame are conducted in VERICUT and then a testing workpiece is machined.All the results show that the algorithm is correct.

5－axis Machine Tool;Spindle－rotating;Post－process;Multi－choice

TP29

A

* 航天复杂结构件高效数控加工示范工程（2011ZX04015－031）

尹春晖，男，1987年生，在读硕士，主要研究方向是数控加工技术。

（编辑 李 静）（

2012－11－28）

130407