Winkler地基上黏弹性输流管的参数共振稳定性

张计光，陈立群，钱跃竑

(1.上海市应用数学和力学研究所，上海 200072;2.日照职业技术学院，山东 276826;3.上海大学 力学系，上海 200444)

输流管道的振动问题在航空航天、海洋工程、石油能源工业、水利工程、生物工程等相关领域中有广泛的应用［1］。管道内流体的流动一般是通过水泵加压作为动力，而由这种脉动动力产生的脉动流引起的管道振动在工程问题中非常普遍且更具有破坏性。

Ariaratnam等［2］对两端支承输流管道的线性方程用辛变换方法和平均法研究了系统的次谐波共振和组合共振。Païdoussis等［3］用实验和线性分析的方法研究了脉动流激励下的管道失稳区域和参数共振现象。Yang等［4］采用梁模型，利用多尺度方法讨论了管道的稳定性问题。

本文研究了黏弹性输流管在Winkler地基上的参数共振稳定性问题。利用直接多尺度方法讨论了输流管的参数稳定性及通过可解性条件得到组合和次谐波共振的稳定性边界。通过数值算例，得到了质量比、黏弹性系数、平均轴向速度、弹性地基对稳定性边界的影响。

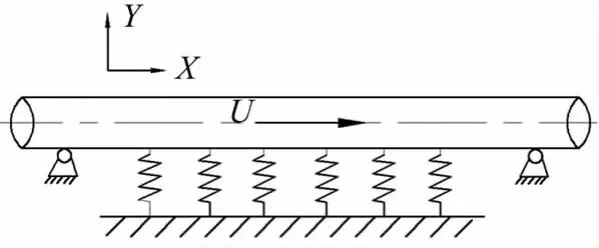
图1 输流管道的物理模型Fig.1 The physical model of pipe conveying fluid

1 数学模型

本文主要研究如图1所示的输流管道，其弹性地基模型为Winkler模型，管道为黏弹性材料，其本构关系采用Kelvin模型。假设管内流体为不可压缩且无黏性流体，忽略重力、管道的剪切变形、截面转动惯量影响的黏弹性输液管［5-6］，在Winkler弹性地基上的控制方程:

其中:EI为管道的弯曲刚度，α为管道的黏弹性阻尼系数，μ为无量纲的滞后阻尼系数，C为管外流体或气体对管道的粘性阻尼系数，Ω为频率，m为管道单位长度的质量，M为管道内流体单位长度的质量，U为管内流体流速，Y(X，T)为管道的横向变形，X和T分别表示轴向坐标和时间，L为管道的长度，K为地基反力系数。

引入如下新的无量纲变量:

得到在Winkler弹性地基上黏弹性输流管的无量纲形式运动微分方程和简支边界条件为:

2 多尺度分析

管道内流体的流速受到周期小扰动:

将式(5)代入式(3)，得:

对式(4)、(6)应用直接多尺度方法，设其一阶近似解为:

式中:T0=t和T1=εt分别为由于固有频率导致的快时间尺度和因阻尼及速度小扰动而引发的振幅、相位变化的慢时间尺度。将式(7)代入式(6)，分离ε0和ε1不同阶量，得到:

输流管道内流体的脉动频率ω接近系统某阶固有频率的两倍或者某两阶固有频率之和时，就会发生共振的现象。引入调谐参数σ，表示脉动频率ω在ωn+ωm附近变化，即:

其中:ωn和ωm分别表示式(8)的第n阶和第m阶固有频率。为分析和式组合共振的响应，设式(8)的解为:

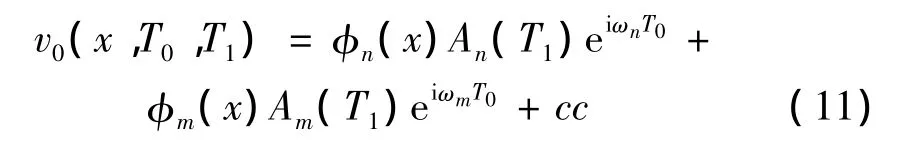
其中:cc表示等式右端之前各项的共轭复数。把式(10)和式(11)代入式(9)，并把右端的三角函数表示为指数形式得到:

其中:符号上的点及撇分别表示对慢变时间T1及无量纲轴向坐标x的导数，NST表示不会给解带来长期项的所有项。若要所得解不存在长期项，则可解性条件要求方程式(12)的非齐次部分与其伴随方程的齐次解正交［7］，即:

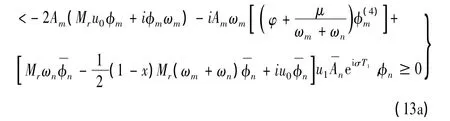
其中:在区间［0，1］上，复方程的内积定义如下:

应用内积的分配律，由式(13)得到:

其中:系数为:

它们由方程式(8)的模态函数和固有频率所决定，与流体速度的脉动量无关。

将振幅写成极坐标形式，做如下变换:

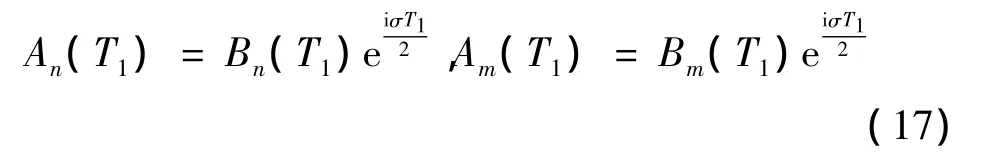
把式(17)代入式(15)中，得自治方程:

易知，式(18)有零解。分析式(18)的非零解情况，设其非零解为:

其中:bn和bm为实数，λ为要确定的复数。把式(19)代入到式(17)，并取第二式的共轭，可以得到:

如果方程(20)有非零解，则它的系数矩阵的行列式为零，即:

如果λ有正实部解，则系统解不稳定，如果λ全部为负实部，则系统稳定。

经数值验证cnm和cmn均为实数，将 λ，dnm和dmn分离为实部及虚部:

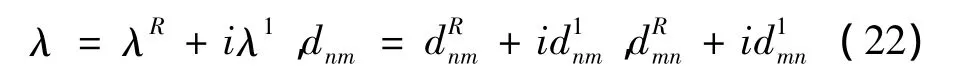
把式(22)代入式(21)，并分离实虚部，得到:

把λR代入式(23)并消去λI得到:

式(24)就是和式组合共振响应失稳区域的边界，即组合或谐波共振失稳的临界条件。当m=n，式(24)简化为n阶谐波共振的临界条件:

3 在两端铰支下输流管道的失稳区域边界及参数影响

设式(8)的解是:

其中:φn(x)和ωn是输流管道的第n阶模态和第n阶固有频率。

将(26)式代入(8)式及边界条件，化简得:

式(27)是四阶常微分方程，其解可以写为如下形式:

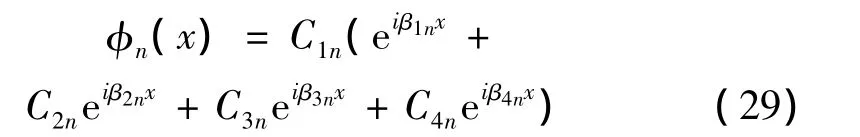
把式(29)代入式(27)、(28)有:

为使原问题有非零解，则线性代数方程(31)的系数矩阵的行列式必须有零解，从而得:

以质量比Mr=0.6，k=20，u0=2.0，c=0.01，φ=0.000 103，μ=0.001 01 的弹性地基输流管道为例，其固有频率为 ω1=8.6950，ω2=37.8439，而模态函数(32)中，第一阶有 β11=3.7010，β21=-2.3152，β31=-0.6929+2.4513i，β41=-0.6929-2.4513i，第二阶有 β12=6.8677，β22=-5.6599，β32=-0.6039+5.9971i，β42=-0.6039-5.9971i。在和式组合共振响应失衡区域边界(24)中，通过数值计算可以得到当m=1，n=2，即第一阶、第二阶和式共振时c12=0.0109，c21=0.1021，d12= -0.2039-2.5097i及d21=-0.0581-0.7150i。在次谐波共振响应失衡区域边界式(25)中，当m=n=1 有c11=0.0109，d11=-0.2039-2.5097i;当m=n=2 有c22=0.1021，d22=-0.0581-0.7150i。

4 数值验证及结果

利用微分求积法对前面运用直接多尺度法得到的近似解析结果进行验证，在数值验证中，取ε=1。输流管的计算区域为0≤x≤1，x方向的网点数为N=11，网点的分布采用非均匀网点布置。表1给出了当Mr=0.6，k=20，c=0.01，φ =0.000103，μ =0.00101 时，在不同速度下用不同方法得到的线性派生系统前两阶固有频率的比较，通过比较发现，用这两种方法得到的结果吻合的非常好。

表1 不同方法下第1阶和第2阶固有频率的结果比较Tab.1 The comparison for the variation of the first two-order dimensionless natural frequencies of the linear generating system

图2 不同质量比对前两阶模态共振失稳区域的影响Fig.2 The effect of mass ratios on the stability boundaries

图3 不同流体速度对前两阶模态共振失稳区域的影响Fig.3 The effect of mass ratios on the stability boundaries

给定k=20，u0=2.0，c=0.01，φ =0.000 103，μ=0.001 01，在不同的质量比下，图2利用多尺度法给出了前两阶模态组合共振及谐波共振在σ–u1平面上的失稳区域。其中点线表示Mr=0.6，虚线表示Mr=0.4，实线表示Mr=0.2。从图中可以看出，给定σ时，不论第一、二阶组合共振还是次谐波共振，随着流体与管道质量比的减小，系统的稳定范围增加;而给定u1导致失稳范围减小。

给定k=20，Mr=0.6，c=0.01，φ =0.000 103，μ=0.001 01，在不同的流体速度下，图3利用多尺度法给出了前两阶模态组合共振及谐波共振在σ–u1平面上的失稳区域。其中点线表示u0=2.3，红色虚线表示u0=2，实线表示u0=1.3。从图中可以看出，给定 σ时，第一、二阶组合共振和第一阶次谐波共振随着流体速度的减小，系统的稳定范围增加;而第二阶次谐波共振恰好相反。

5 结论

当同时考虑各种阻尼及弹性地基的影响时，本文研究了两端铰支输流管道在脉动内流作用下的参数共振。对黏弹性输流管道横向振动的控制方程，应用直接多尺度法，得到了可解性条件，推导了包含各种阻尼、平均流速、质量比、弹性地基等参数影响的管道系统前两阶次谐波共振和组合共振的稳定性边界条件，考察了系统的各种参数对稳定性边界条件的影响，并且通过微分求积法和直接多尺度法得到的前两阶固有频率结果进行对比。利用数值计算，发现流体与管道的质量比Mr对系统的稳定性有较大影响，质量比Mr越小，系统越稳定，并且对二阶谐波共振的影响比一阶谐波共振影响要大得多。

［1］ Xu J，Yang Q B.Recent developent on models and nonlinear dynamicsofpipes conveying fluid［J］. Advances in Mechanics，2004(34):182-194.

［2］ Ariaratnam S T，Namachchivaya N S.Dynamic stability of pipes conveying pulsating fluid［J］.Journal of Sound and Vibration，1986(107):215-230.

［3］ Païdoussis M P，ISSID N T.Dynamic stability of pipes conveying fluid［J］.Journal of Sound and Vibration，1974(33):267-294.

［4］ Yang X，Yang T，Jin J.Dynamic stability of a beam-model viscoelastic pipe for conveying pulsative fluid［J］.Acta Mechanica Solida Sinica，2007(20):350-356.

［5］ Rinaldi S，Prabhakar S，Vengallatore S，et al.Dynamics of microscale pipes containing internal fluid flow:Damping，frequency shift，and stability［J］.Journal of Sound and Vibration，2010(329):1081-1088.

［6］ Yoon J，Ru C Q，Mioduchowski A.Vibration and instability of carbon nanotubes conveying fluid［J］.Composites Science and Technology，2005(65):1326-1336.

［7］ Chen L Q，Tang Y Q，Lim C W，Dynamic stability in parametric resonance of axially accelerating viscoelastic Timoshenko beams［J］.Journal of Sound and Vibration，2010(329):547-565.