史灌河河道水流运动特性浅析

阮国余 刘士和

（中水淮河规划设计研究有限公司 蚌埠 233000 武汉大学水利水电学院 武汉 430072）

史灌河河道水流运动特性浅析

阮国余 刘士和

（中水淮河规划设计研究有限公司 蚌埠 233000 武汉大学水利水电学院 武汉 430072）

通过建立非恒定流数学模型，采用有限体积法对水流运动数学模型的控制方程进行离散，用基于同位网格的SIMPLE算法处理流量与水位的耦合关系，全面系统地对史灌河不同流量条件下的各水力要素进行计算，并结合地形资料及实测水文资料进行验证，分析各种不同水情、不同工况条件下的洪水运动规律，为史灌河河道治理规划设计提供技术支撑。

史灌河 数学模型 水流运动特性 河道

1 河流概况

史灌河为淮河南岸最大的支流，是淮河干流洪水的主要来源之一。史河发源于大别山北麓的安徽省金寨县牛山，灌河发源于河南省商城县黄柏山，两条河在固始县蒋集汇合后称史灌河，后向北直下于固始三河尖陈村入淮河。

史灌河流域东邻淠河水系，西接白露河水系，南依大别山山脉，北抵淮河。流域跨安徽省金寨县、霍邱县及河南省固始县、商城县，流域面积6895km2，流域上游为山区，中游属丘陵区，下游为平原。史河上游建有梅山水库，控制流域面积1970km2；灌河上游建有鲇鱼山水库，控制流域面积924km2；两水库控制流域面积占全流域的42%，库区以下还有约4000km2。史灌河较大支流包括：长江河、羊行河、急流涧河、石槽河、响水河、泉河。史河干流出梅山水库后，北流10km至红石咀渠首枢纽，继续北流31.5km有黎集渠首枢纽，流经固始县城后，至蒋集与灌河相汇，经霍邱县临水集汇泉河后，在固始县三河尖入淮河。梅山水库至三河尖的河道长度约为123km。

史灌河为宽浅式游荡型河道，河道宽400～1200m。河床表层土以灰黄、黄色的粉细砂为主，结构松散，透水性强，抗冲能力较低，往往小水过后淤成堆，大水来了冲成潭。复杂的地质条件是河道险工形成和发展的主要原因。

史河河道长江河口～叶集孙家沟段，由于有序采砂（用于建筑、制砂砖等），主槽较为明显，且主槽断面较大；叶集孙家沟～固始段河道，铁砂位于黄砂下部，由于当地群众翻采铁砂，该段河道出现无数小砂堆，主槽不明显，且无规律；固始以下段河道，河床中部有断续砂丘，河道主槽较为明显。

史灌河左堤长江河口～响水河口段，除钓鱼台～朱店（长约2km）、石槽河～状元桥（长约2km）、牛客坟～杨庙（长约1km）段均为以岗代堤段外，其余段均有堤防；响水河口以下为以岗代堤段无堤防。右堤陈淋大桥～五里拐子段堤防为安徽境内堤防，标准较高，且坡面均进行了块石护砌；五里拐子～黎畈段（长约1.5km）为以岗代堤段；黎畈～幸福闸段除南园～龙潭寺（长约1.5km）段为以312国道代堤段外，其余段均有堤防；幸福闸以下无堤，堤防折向东与泉河左堤相连接。

2 数学模型与数值计算方法

2.1 数学模型

一维非恒定流运动数学模型的控制方程如下：

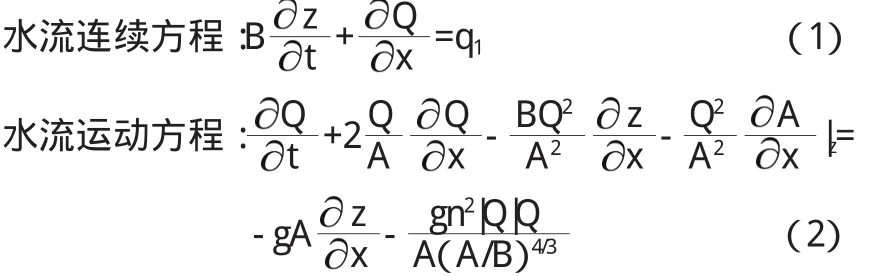
式中：x表示沿流向的坐标；t表示时间；Q表示流量；z表示水位；A表示过水断面面积；B表示河宽；ql为沿程单位河长流量变化；n为糙率。

一维非恒定流边界条件包括进口边界和出口边界，进口边界一般给定流量过程；出口边界一般给定水位过程。

2.2 数值计算方法

以计算河段为控制体，采用有限体积法对前述水流运动数学模型的控制方程进行离散，用基于同位网格的SIMPLE算法处理流量与水位的耦合关系。

2.2.1 水流运动方程

将水流运动方程沿控制体积分，对流项采用一阶迎风格式，水流运动方程式（2）的离散形式如下：

其中：AW=max（Fw，0）

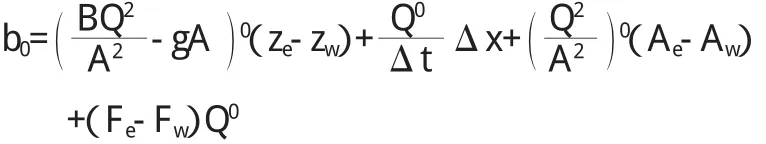
式中：φ为通用控制变量；Fw，Fe为界面质量流量；Δx为控制体长度；Δt为计算时间步长；上标0表示变量采用上一时间层次的计算结果。

在求解过程中，为增强计算格式的稳定性，采用了欠松弛技术，将速度欠松弛因子α0代入式（3）即可得到水流运动方程的最终离散形式：

2.2.2 水位修正方程

根据动量插值的思想，引入界面流量计算式和流量修正计算式如下：

式中：AP为运动方程主对角元系数。

将求解动量方程所得的流速初始值和上一层次的水位初始值代入上式即可得到界面流量Q*e，将Q*e+Q'e代入连续方程即可得到水位修正方程如下：

式中：上标P表示水位修正方程的系数，且

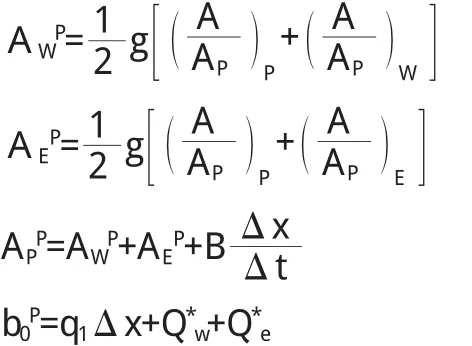
在求得水位修正值之后，分别按照下式修正水位和速度：

水利枢纽段的水流运动计算由水位～流量关系来确定。

3 工况选取与计算

3.1 工况的选取

根据史灌河的特点，共选定以下3种工况进行计算，3种工况的洪水重现期分别为：10年一遇（工况1）、20年一遇（工况2）和50年一遇（工况3）。

3.2 计算成果

采用所建立的数学模型，对各工况下的洪水演进进行计算，下面从洪峰流量、最高洪水位、各特征点洪水过程三方面对计算成果加以描述。

3.2.1 洪峰流量

水流自梅山水库出库后，随着支流洪水的不断汇入，史河（史灌河）洪峰流量总体上呈不断增加的趋势。就洪峰流量的沿程变化来看，至固始七一大桥，在10年、20年与50年一遇洪水条件下，其洪峰流量分别为2683m3/s、3265m3/s和4169m3/s；至灌河口，随着灌河的汇入，从沿程变化来看洪峰流量达到局部最大值，在10年、20年与50年一遇洪水条件下，其值分别为3297m3/s、4134m3/s和5361m3/s；在灌河口以下，洪峰流量有所减小，但随着泉河的汇入，洪峰流量又有所增加。对灌河而言，最大洪峰流量与鲇鱼山水库出流流量基本相当。

3.2.2 最高水位

从史河（史灌河）最高洪水位的沿程变化来看，水流自梅山水库出库后受重力作用向下游运动，最高洪水位沿程降低，至固始七一大桥，对10年、20年与50年一遇的洪水，其最高洪水位分别为36.13m、36.77m和37.55m；至灌河口，对10年、20年与50年一遇的洪水，其最高洪水位分别34.16m、34.87m和35.71m。灌河最高洪水位也呈沿程降低的趋势，至无量寺，对10年、20年与50年一遇的洪水，其最高洪水位分别为39.96m、39.96m和40.36m。

3.2.3 洪水过程

随着支流洪水的不断汇入，史河（史灌河）蒋集以上特征点的洪峰流量总体上沿程逐渐增加，洪峰出现时间逐渐延迟，流量过程线越来越尖瘦；而在蒋集以下，流量过程线的变化则不甚明显；灌河流量过程主要受鲇鱼山水库出流及灌河口水位顶托影响。

史河（史灌河）水位过程线沿程变化以蒋集为界，蒋集以上水位过程线沿程越来越尖瘦，蒋集以下的水位过程线沿程则越来越坦化；灌河水位过程主要受鲇鱼山水库出流及灌河口水位顶托影响。

3.2.4 流速变化

各工况下史河（史灌河）各特征点的最大流速变化过程如下：

（1）10年一遇的洪水：史河（史灌河）断面平均流速位于0.13～1.39m/s的范围内，最大流速（沿程变化）出现在黎集枢纽，为1.39m/s；最小流速（沿程变化）出现在泉河口，为0.13m/s。

（2）20年一遇的洪水：史河（史灌河）断面平均流速位于0.17～1.51m/s的范围内，最大流速（沿程变化）出现在黎集枢纽，为1.51m/s；最小流速（沿程变化）出现在泉河口，为0.17m/s。

（3）50年一遇的洪水：史河（史灌河）断面平均流速位于0.22～1.67m/s的范围内，最大流速（沿程变化）出现在固始七一大桥，为1.67m/s；最小流速（沿程变化）出现在泉河口，为 0.22m/s。

（4）从灌河沿程变化来看，断面平均流速以无量寺处为最大，相应于10年、20年与50年一遇洪水其值分别为1.64m/s、1.64m/s和 1.72m/s。

4 结论

（1）采用有限体积法对一维水流运动数学模型进行了离散，其中对流项采用延迟修正的二阶格式，同既有的离散方法相比，该方法物理概念清晰，计算格式的数值稳定较好。采用实测水文资料对该报告所建立的数学模型进行了验证，验证成果表明，各测站水位过程和流量过程的计算成果与实测成果吻合较好。

（2）随着支流洪水的不断汇入，史河（史灌河）蒋集以上各特征点的洪峰流量总体上沿程逐渐增加，洪峰出现时间逐渐延迟，流量过程线越来越尖瘦；而在蒋集以下，流量过程线的变化则不甚明显，在三河尖随着泉河的汇入，洪峰流量达到最大值。史河（史灌河）水位过程线沿程变化以蒋集为界，蒋集以上水位过程线沿程越来越尖瘦，蒋集以下的水位过程线则沿程越来越坦化。

（3）灌河的流量过程与水位过程主要受鲇鱼山水库出流及灌河口水位顶托影响。

（4）史河（史灌河）的断面平均流速具有如下变化趋势，在10年与20年一遇洪水条件下，以黎集枢纽处为最大；而在50年一遇洪水条件下，则以固始七一大桥为最大。灌河断面平均流速以无量寺为最大

（专栏编辑：顾 梅）