基于径向基函数的高效网格变形算法研究
2013-09-09安效民
谢 亮,徐 敏,张 斌,安效民
(西北工业大学 航天学院,西安 710072)
在非定常流动模拟、流固耦合时域仿真、气动外形优化中,为了使得计算网格适应物面边界的变化,可以采用网格重构的方法,然而更广泛的是应用网格变形技术,这样可以保留原始网格的拓扑结构与密度、正交性等特性,不会在求解器中引入额外的误差,同时计算量较小。目前存在多种网格变形方法,无限代数插值方法[1]计算量较小,然而却仅适用于结构网格,且难于处理复杂的拓扑结构,通用性不好。对于非结构网格、混合网格,可以应用弹性体方法[2]、弹簧比拟法[3-4]以及Delaunay图映射[5]方法。弹性体方法将网格所占据的区域比拟为一个弹性体,通过采用有限元或者边界元方法求解弹性体的变形来实现动态网格变形技术,通用性较好,效果优良,变形后的网格质量极好,尤其适用于大变形情况,然而计算量非常庞大。弹簧比拟法将网格线比拟为弹簧,通过求解弹簧变形后的平衡位置实现网格变形,其通用性较好,适用于任意网格,网格变形后的质量也较好,然而其计算量仍然较大,且难于处理大变形问题。Delauny图映射方法鲁棒性与效率较好,但是对于大变形问题仍然难以处理。
近些年来,由于具备诸多优良的特性,基于径向基函数的网格变形技术得到了极大的发展[6-9]与广泛的应用[10-12]。其主要思想是利用已知的物面网格变形,构造一个径向基函数序列,再使用此径向基函数序列将物面变形光滑地插值到空间气动网格上去。此方法计算过程中不需要利用网格节点之间的联系,各个计算结点的变形计算是完全不相干扰的,因此非常便于并行化;可支持复杂外形的大变形运动,变形后的网格质量较好,通用性与鲁棒性极好;编程也较方便,易于实现;物面与空间网格节点的处理采用一样的方式,因而不需要额外的数据插值方法;既可用于结构网格,也可用于非结构与混合网格;可支持任意形式的变形,刚体运动、弹性变形甚至塑性变形都可支持。然而,采用径向基函数进行网格变形时的计算量与Nvp×Nsp成正比,其中Nvp是待插值的气动空间网格点数,其量级一般在105~106,Nsp是用于插值的表面节点数,其量级一般在102~103,相较于代数插值方法,其计算量是相当大的。在过去的数年间,为了减少计算量,不少研究员[6-8]做出了相当多的努力。其中,Rendall等[6-7]采用贪心算法,在物面插值过程中将出现最大误差值的点纳入插值节点集合中,从而在保证精度的前提下选择得到尽可能少的物面插值节点,以此来减少总的计算时间。最近,王刚等[8]将Rendall提供的算法加以改进,引入子空间逐级逼近的思想,每一次插值过程中选择一插值节点集合,下一次插值时以上一次插值过程中在物面产生的误差作为插值对象,从而将选择插值节点的时间大为减少。然而目前来看,为了达到减少计算量,几乎所有的文献都集中在减少表面插值节点的数目上,而少有人考虑在插值过程中减少空间待插值节点的方法,仅见有Andreas[9]为了分离飞行器部件运动对其它部件的影响,提出过限制径向基函数插值区域的算法。
本文受王刚在选择表面插值节点过程中引入子空间逼近的思想的启发,同时将Andreas提出的限制径向基函数插值区域的方法加以改进,两者结合,提出了在计算过程中逐级减少空间待插值节点的方案,此方案不损失插值精度,且支持大变形。算法的关键在于在选择表面插值节点个数的时候,随着插值节点个数的逐步增加,插值误差会逐步减少,当以前一步插值过程中产生的插值误差为插值对象的时候,此时的插值限制区域可以取得较小,这样就可以使得当Nvp比较大时,Nsp比较小,而Nvp比较大时,Nsp比较小,从而减少总的计算量。算例结果表明本文提出的方案可以显著地提高采用径向基函数进行网格变形时的计算效率,同时保留对大变形问题的支持及插值精度。
1 采用径向基函数进行网格变形
径向基函数的基本形式是[8]:
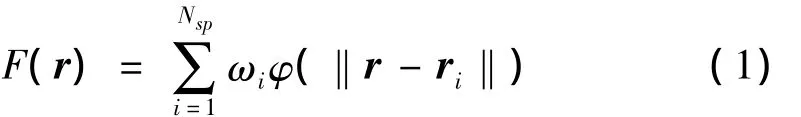
式中:F(r)是插值函数,在网格变形问题中,它代表网格变形量;Nsp代表插值问题所使用的径向基函数的总数目,在网格变形问题中,它等于用于插值的物面节点数;φ(‖r-ri‖)是径向基函数的一般形式,ri是第i个物面插值节点的位置,r是空间任意一点的位置矢量,进行网格变形时,它就是CFD网格空间节点的位置矢量,‖r-ri‖是空间任意一点到第i个物面插值节点的距离;ωi是与第i个插值节点相对应的权重系数。径向基函数有许多种,文献[6]列出了数种形式,经比较认为Wendland's C2函数计算效率与网格变形的质量都较好,故而本文采用它作为径向基函数来实施网格变形,其形式如下[6,8]:
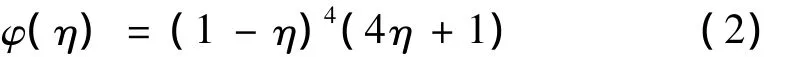

给定物面插值节点及该点上的位移后,采用式(1)、(2)求解空间任意一点的变形时,r,ri已知,且径向基函数φ(η)已经给定,故而唯一未知的是与各个物面插值节点相关的权重系数ωi,该值可以使用物面上的插值结果必须与给定位移相吻合这一条件来求得,即求解下述方程即可:

式中,下标s代表物面插值节点,
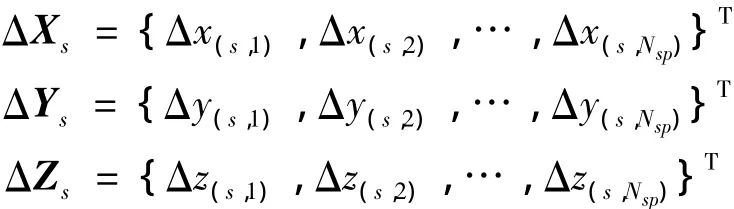
表示Nsp个物面插值节点上的位移,
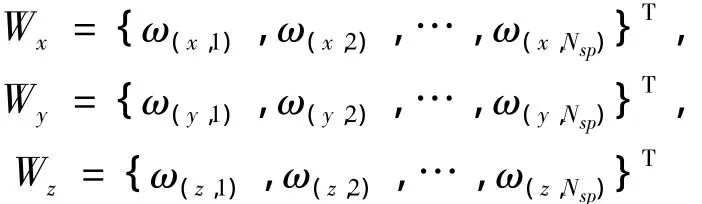
是与每一插值节点相关的权重系数,未知。矩阵中每一元素是以表面插值节点中任意两节点之间距离为参数的径向基函数值,即:
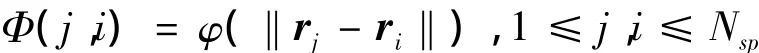
求解方程(3)~(5)后可得到权重系数,然后根据式(1)可求得空间任意位置上的网格变形。
2 表面插值节点的选择方法
采用径向基函数进行动态网格变形时,计算量与Nvp×Nsp成正比,其中Nvp是待插值的气动空间网格点数,Nsp是用于插值的表面节点数,在流固耦合时域仿真时,它一般取自结构模态。为了减少总的计算量,当前主流做法是减少Nsp的值,Rendall等[6-7]采用贪心法根据最大插值误差位置逐步添加插值节点的方法来实现径向基函数序列的精简。其基本过程是:
首先,任意选择Ⅰ(一般可取Ⅰ=3)个物面节点形成初始节点集合P0=(p1,p2,…,pI),采用此集合进行径向基函数插值,通过求解方程得到相应的权重系数,然后求得所有物面节点上的网格变形,显然这样建立的初始插值函数对于P0中的所有节点是精确的,但是对于不属于P0中的物面节点将产生误差,确定出现最大误差的物面节点,根据贪心法的原则,将此节点纳入P0中形成下一个节点集合P1,再次采用此节点集合P1进行径向基函数插值。反复执行此过程直到物面节点上的插值误差满足事先给定的误差限。在选择物面节点过程中亦可以每插值一次,将误差大于平均误差或者给定的一个限值的所有物面节点都选择到插值节点集合中;或者混合上述两种方法,每n步交替使用此两种方法,n步内选择误差最大的节点,第n+1步选择误差较大的一些节点,以加快选择节点的速度。
最近,为了加快数据精简的效率,王刚等[8]提出了一套新的数据精简方法,其基本思想是按照贪心法的原则,引入函数空间子集逐级逼近的基本思想,具体做法是先选择N0个节点进行径向基函数插值,得到所有物面节点上的误差ΔS(0),然后将径向基函数的插值对象由最初的网格变形更改为当前物面节点的误差ΔS(0),再次运用贪心法选取N1个物面节点进行插值。重复此步骤直到残差满足要求,最后将此n步选择得到的插值节点和权重系数迭加,得到最终的径向基函数插值系数。采用此种方法的目的在于加快数据精简的效率,因为在计算插值系数的过程中,每一次都要求解一个Ni×Ni的线性代数方程组,通过此种算法,可以将每一次计算插值系数过程中的Ni值控制在一个较小量上,由此加快数据精简过程。然而我们将看到,将函数空间子集逐级逼近的思想加以扩展,可以得到一种减缩空间待插值节点的方法。
3 空间待插值节点的减缩方法
目前,为了减少采用径向基函数进行网格变形的计算量,研究人员的着眼点都集中在减少Nsp即表面插值节点上,但是对于在实施径向基函数过程中如何减少Nsp,却少有人提及。目前仅见有 Andreas[9]为了分离单个部件运动对其它部件的影响提出了限制径向基函数插值区域的算法。其算法的基本思想是将部件的运动限制区域以长方体描述,该长方体包括了运动部件区域,运动部件上的变形以给定为要求值,长方体表面上的变形给定为零,在长方体表面与运动部件上选择插值节点后进行径向基插值,长方体外的空间网格不作插值。
将函数空间子集逐级逼近加以扩展,并将Andreas提出的限制插值区域的方法加以改进,两者相结合,得到了一种新的效果优良的减缩Nvp的方法,可支持大变形运动。方案主要步骤为:
(1)确定插值限定区域Ω0,不同于文献中的做法,本文选择到物面距离小于一限制值R0=k·ΔSmax的点的集合作为Ω0,其中k为一系数,一般取k≥5。并确定Ω0中除去物面的边界,可按下列方法确定此边界,扫描Ω0内各点,如果某点周边单元上的节点中有不属于Ω0的节点,则此点为边界,否则是内点,将边界上的位移值给定为0。给定一个初始误差限E0,此误差可取得较大,比如1.0E-2,选择N(0)个插值节点使得表面插值误差的最大值小于此给定误差限,并记录表面插值误差ΔS0。在区域Ω0内进行插值,此时,Nsp较大,Nsp=N(0),由于误差限取得较大,求得的N(0)会比较少,即总计算量会比较少。
(2)再以上一步的表面插值误差ΔS0为插值对象,确定插值限定区域Ω1。由于此时表面插值量最大位移才不到E0,同样按到物面距离小于R1=k·ΔS0,max为标准,由于此时 ΔS0,max≤E0,故而此时的 Ω1可以取得较小,从而使得Nvp较小,这时可以给定一较小的误差限E1来选择N(1)个插值点,由于误差较小,故选择得到的N(1)较大。然而总的计算量仍然会比较小。
(3)重复上述步骤直到误差限满足要求。
需要注意的是,当Ri较小的时候,插值区域限定过小,区域外边界与物面距离过近,使得选择的插值节点中有些节点之间距离过近,会造成求解插值系数时系数矩阵十分病态,因此,实际上对于Ri有一限制,本文限定为Ri=k1·max(Ei-1,dmax),其中k1为一保险系数,一般取为2,Ei-1为上一步的误差限,而dmax为与物面相连的最长网格线的长度。加上此限制之后,一般第二次插值时Ri即达到限制值了,因此,第三步就用不着了。同时应当注意的是,在插值区域的外边界上选择插值节点时,并不要求在此边界上的误差与物面上保持同样小的误差,仅需此边界上的误差不造成该边界附近网格质量出现较大下降,因此,该边界上插值节点的选择以保证该边界上最大误差小于附近单元尺寸最小值的k倍,k可取0.1。这样可以避免插值过程中Nsp较大。
(4)如果最后一次插值中误差限已经衰减到远小于空间网格点到物面的最小距离了,此时可选择更多的插值点,但是仅在物面进行插值,进一步减小物面插值的误差,因为此时物面的变形不会造成空间网格的扭曲。这时Nvp就等于气动网格的物面网格数了,这一步计算量会比较小,然而可以较大程度地减小整个物面的插值误差。
在上述过程中,确定插值限定区域的计算量较大,但是此过程仅实施一次,之后每一次网格变形时的限定区域都与初始确定的区域一致,因此这一步的计算时间并不增加多次执行的网格变形所需要的时间。
4 算例
4.1 NACA0012翼型变形
取二维NACA0012结构网格作为初始网格,变形位移方程为 Δy=0.03sin(4πx)[8]。网格大小为 323 ×81,取误差限为1E-6,分别采用单次插值与本文所提出的多次插值方法进行计算,在计算过程中,多次插值中第一次插值由于本来变形比较大,且远场网格本身比较稀疏,简单起见,直接将全场网格当做Ω0,在第二次插值中减缩空间网格点数,选择Ω1中包含3 553个网格节点,第二次插值计算完毕后,物面插值误差限已经足够小,因此第三次插值只计算物面网格变形,不用计算Ω2。插值效率的比较见表1,可见本文提出的方法确实较好地提高了径向基函数的插值效果,对于多次插值中的第二次插值,虽然表面插值节点较多,但是由于空间待插值节点大幅减少,效率仍然得到提高,而第三步由于空间插值节点数退化为表面插值节点数,效率提高得更加明显,从而印证了本算法思路的正确性。网格变形结果见图1。

图1 NACA0012翼型变形前后对比Fig.1 Comparison of deforming grid for naca0012 foil

表1 完成NACA0012翼型网格变形所需时间的比较Tab.1 Comparison of efficiency between one interpolation and multi-level interpolation for grid-deforming of naca0012 foil
4.2 ONERA-M6机翼变形

取ONERA-M6机翼非结构网格为初始网格,机翼几何形状与参数见文献[13],网格单元数为1 883 014,结点数为336 684,物面节点数为33 206,给定以下变形模式:其中:b为机翼展长,z为z方向坐标,Δy为y方向变形。取最终误差限为1.0E-6,分别采用单次插值与本文所提出的多次插值方法进行计算,计算过程与上例相同。计算过程所花费的时间与单次插值效率的比较见表2,由表可知本文所提出的多次插值方法可以较大程度上减少空间待插值网格数,从而显著地提高了网格变形效率。初始网格与变形后网格的比较如图2所示。图2(a),(b)对比了初始的与变形后的表面网格,可见式(6)所给出的变形幅度是相当大的。图2(c),(d)分别给出了机翼附近空间网格变形前后的情况,图2(e),(f)分别给出了翼梢附近网格变形前后的细节,可见变形后的网格基本保持了变形前的密度分布,且质量较好。经流场求解程序的检验,变形后的网格质量没出现问题。

图2 ONERA-M6机翼网格变形前后对比图Fig.2 Comparison between original and deforming grid of ONERA-M6 wing
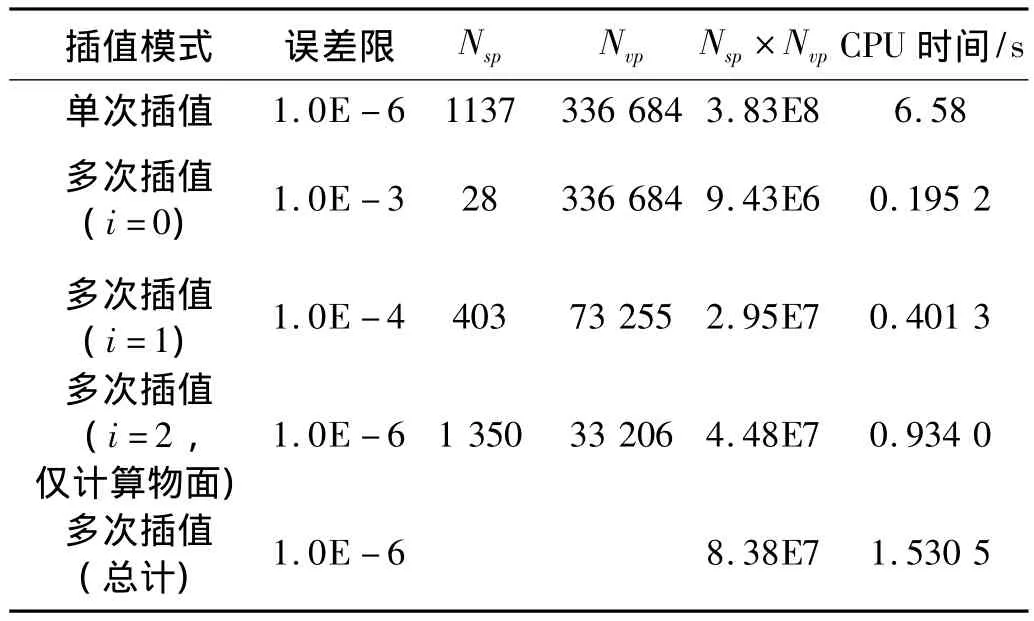
表2 完成ONERA-M6机翼网格变形所需时间的比较Tab.2 Comparison of efficiency betweenone interpolation and multi-level interpolation for grid-deforming of ONERA-M6 wing
5 结论
本文对于采用径向基函数进行动态网格变形技术中如何减少计算量的问题进行了研究,与目前多数文献的着眼于表面插值节点数不同,本文在减少表面插值节点数的时候也试图减少空间待插值节点数,采用函数子空间逐级逼近的基本思想,每一次网格变形后,下一次网格变形的目标更改为上一次产生的表面误差,且每一次网格变形时的限定区域随着误差的减小而逐渐减小,由此使得空间待插值节点数较大时,表面插值节点数较小;表面插值节点数较大时,空间待插值节点数较小,从而节省了总的计算时间。算例结果表明:本文提出的网格变形算法在保证精度的同时,可以显著的节省计算时间,并能支持大变形运动,且变形后的网格质量仍然合乎要求。
[1] Li J,Huang S Z,Jiang S Q,et al.Unsteady viscous flow simulations by a fully implicit method with deforming grid[M].AIAA 2005-1221.
[2]张 军,谭俊杰,褚 江,等.一种新的非结构动网格生成方法[J].南京航空航天大学学报,2007,39(5):633-636.
ZHANG Jun,TAN Jun-jie,CHU Jiang,et al.New method for generating unstructured moving grids[J].Journal of Nanjing University of Aeronautics & Astronautics,2007,39(5):633-636.
[3]刘 君,白晓征,郭 正.非结构动网格计算方法-及其在包含运动界面的流场模拟中的应用[M].长沙:国防科技大学出版社,2009.
[4]霍世慧,王富生,岳珠峰.弹簧近似法在二维非结构动网格生成技术中的应用[J].振动与冲击,2011,30(10):177-182.
HUO Shi-hui, WANG Fu-sheng, YUE Zhu-feng. Spring analogy method for generating of 2D unstructured dynamic meshes[J].Journal of Vibration and Shock,2011,30(10):177-182.
[5]伍贻兆,田书铃,夏 键.基于非结构动网格的非定常数值模拟方法[J].航空学报.2011:32(1):15-26.
WU Yi-zhao,TIAN Shu-ling,XIA Jian.Unstructured grid methods for unstready flow simulation[J].Acta Aeronautica et Astronautica Sinica,2011,32(1):15-26.
[6] Rendall T C S,Allen C B.Efficient mesh motion using radial basis functions with data reduction algorithms[J].Journal of Computational Physics,2009,229(7):6231-6249.
[7]Rendall T C S,Allen C B.Reduced surface point selection options for efficient mesh deformation using radial basis functions[J].JournalofComputationalPhysics,2010,229(8):2810-2820.
[8]王 刚,雷博琪,叶正寅.一种基于径向基函数的非结构混合网格变形技术[J].西北工业大学学报,2011,29(5):783-788.
WANG Gang, LEI Bo-qi, YE Zheng-yin. An efficient deformation tachnique for hybrid unstructured grid using radialbasis functions[J]. Journal of Northwestern Polytechnical University,2011,29(5):783-788.
[9]Andreas K M.Aircraft control surface deflection using RBFBased Mesh deformation.
[10] Beckert A,Wendland H.Multivariate interpolation for fluitstructure-interaction problems using radial basis functions.
[11]de Boer A,van der Schoot M S,Bijl H.Mesh deformation based on radial basis function interpolation[J].Computers &Structures,2007,85:784-795.
[12] Rendall T C S,Allen C B.Parallel efficient mesh motion using radial basis functions with application to multi-bladed rotors[J].International Journal for Numerical Methods in Engineering.2010,81:89 ~105.
[13]Schmitt V,Charpin F.Pressure Distributions on the ONERAM6-Wing at Transonic Mach Numbers[R].Experimental Data Base for Computer Program Assessment.Report of the Fluid Dynamics Panel Working Group 04,AGARD AR 138,May,1979.
