基于重构相空间短时状态预测残差的直升机旋翼损伤跟踪方法

朱旭程，马 强，侯志强

(海军航空工程学院 飞行器工程系，山东 烟台 264001)

旋翼是直升机飞行的关键动力部件，在桨叶周期变距和气动交变载荷作用下，桨叶、桨毂、减摆器及变距拉杆等会出现磨损与疲劳失效故障。旋翼故障为高等级危险故障。准确监测旋翼的损伤状况，对提高直升机飞行安全极具现实意义。Azzam等［1］研究旋翼损伤监测，提出通过桨叶相对位移与机体振动识别旋翼故障方案。Ganguli等［2-3］分析了典型损伤对旋翼气弹响应信号影响，运用神经网络、模糊推理等人工智能技术建立旋翼故障诊断算法。在飞行条件下对旋翼损伤进行检测尚存技术瓶颈［4］:① 在高速旋转的旋翼上直接加装各种数据采集系统遭技术限制。直升机健康及使用监测系统(Health and Usage Monitoring System，HUMS)主要通过在机身上安装传感器获得旋翼状态数据，可用信号种类较有限;②因桨距时变、气弹耦合及非定常尾流等因素影响，用传统数据分析方法难以获得对损伤敏感而对正常状态扰动、噪音、建模误差不敏感的旋翼损伤观测信号，缺乏有效的旋翼损伤跟踪方法。为此，本文用源自混沌理论的相空间重构技术，将旋翼状态监测数据变换到更高维数的状态空间内，以不同时间尺度研究旋翼系统的损伤演化过程。以旋翼实测相轨迹与基准旋翼状态短时预测模型计算相轨迹之差异作为新损伤观测信号，提出新的旋翼损伤跟踪方法。此法可根据单个旋翼状态监测信号的时序数据在相空间中重建旋翼系统的动力学本质，对旋翼的状态监测更有效。

1 旋翼在重构相空间的损伤演化特性

1.1 旋翼气弹有限元模型

为对比分析健康与损伤旋翼的动态特性，研究损伤对桨叶位移、桨毂力等旋翼状态监测信号影响，建立旋翼气弹有限元模型。由Hamilton能量变分原理得:

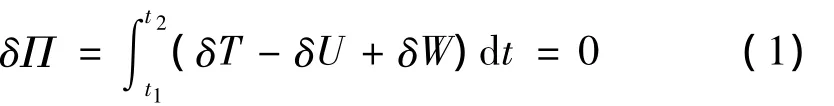
式中:Π为系统总能，T为动能，U为应变能，W为外力虚功，气动载荷采用叶素理论建立，旋翼诱导速度采用White-Blake入流模型［5］计算。用有限元方法离散能量积分，用分部积分法建立旋翼气弹有限元方程为:

式中:M、C、K、F分别为惯性矩阵、阻尼矩阵、刚度矩阵及载荷向量，在定常平飞状态下为方位角的周期函数。旋翼气弹有限元方程可采用时域有限元方法化为代数方程求解，或将其转换为非线性状态方程用数值积分方法求解。

旋翼故障模式种类较多，不同类型的故障对系统参数影响不同。采用复合材料桨叶刚度疲劳损伤演化模型为:

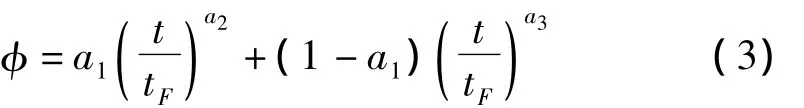
图1 桨叶刚度损伤变量扩展曲线Fig.1 Damage accumulation curve of blade stiffness

直升机HUMS系统能直接提供的旋翼状态监测信号主要有二类:一类为桨叶挥舞、摆动及扭转位移，可通过在机身上安装激光多普勒测振仪实时监测［6］;另一类为桨毂力及力矩，可通过机身上的应变计或振动传感器结合飞行参数获得。

以桨尖位移、桨毂力及力矩作为旋翼典型状态监测信号，将旋翼气弹有限元模型与桨叶损伤演化模型相结合，可计算分析桨叶损伤对桨尖位移及桨毂载荷影响。本文以BO-105直升机旋翼为参考设置实例旋翼基本参数为:桨叶数4，旋翼半径R=4.94 m，旋翼转速 Ω=40 rad/s，桨叶密度m=6.46 kg/m，桨叶弦长0.055 R，弦向刚度 0.026 8 mΩ2R4，挥向刚度 0.010 8 mΩ2R4，扭转刚度0.006 15 mΩ2R4，洛克数5.2，桨叶升力线斜率6.0，型阻系数 0.002，诱导阻力系数 0.2，俯仰力矩系数0.00。飞机在前进比0.3、旋翼拉力系数0.004 9条件下定常平飞。旋翼仿真程序用Matlab软件建立(图2)，主程序先调用公式推理模块执行符号积分及微分，算出各单元惯性矩阵、刚度矩阵及载荷向量，桨叶挥舞、摆动位移形函数用3次Hermitian多项式，扭转位移形函数用2次Lagrangian多项式以保证弯、扭力矩变分的线性一致。为加快计算收敛过程引入比例阻尼，载荷向量含环量、非环量气动载荷及节点位移的非线性项，诱导速度用内嵌的迭代过程计算。主程序在龙格-库塔积分步中循环调用右侧函数模块求解状态方程积分。右侧函数模块消除单元矩阵及向量中的桨叶方位角等符号变量后，装配生成整体矩阵并用高斯消元法求出状态增量，最后采用求和法计算出桨毂载荷。桨叶在健康(t/tF=0)与损伤(t/tF=1/3)状态下仿真产生的桨尖位移、桨根力及力矩如图3所示。图中，w为桨尖挥舞位移，v为桨尖摆动位移，Fz为桨毂力，Mx为桨毂力矩，n为样本长度。

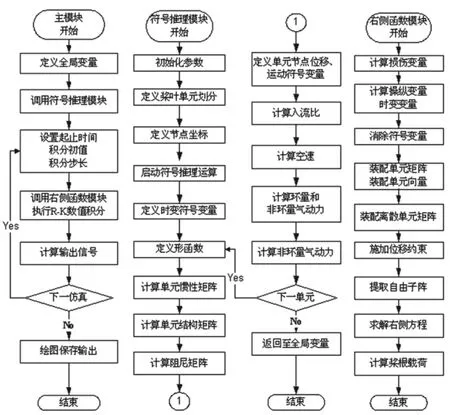
图2 旋翼仿真程序流程Fig.2 Flowchart of rotor simulation procedure

1.2 旋翼状态监测信号相空间重构

旋翼损伤监测的基本问题为能找到对损伤敏感而对系统状态变化、干扰噪声不敏感的观测信号。而桨叶损伤与气弹耦合现象会引起气动载荷沿桨叶结构分布发生变化［7］，随着桨叶损伤程度的扩展，在挥舞、摆动、扭转方向的固有频率互相穿越与交叉，使桨尖位移与桨毂载荷峰值等特征信号在单调性关系上出现突变，难以据该特征信号辨识出损伤的变化趋势。源自混沌理论的相空间重构技术可在不同维数空间内、以不同时间尺度研究演化系统的动力学特性。只要时间尺度与空间维数选择合适，即可望通过相轨迹的移动变化定量跟踪系统损伤的演化过程。将某监测信号时序数据{y(i):i=1，2，…，M}进行时间坐标延迟，构造一状态点列 {x(n):n=1，2，…，N}。其中，x(n)= ［y1(n)，y2(n)，…，ym(n)］T，yk(n)=y［n+(k-1)τ］，m为嵌入维数，τ为延迟时间。该点列描述系统在m维状态空间中的相轨迹，由其构成的空间称为相空间，此过程称相空间重构。据嵌入理论［8］，若重构系统与原动力学系统的动态响应可限制在相同维数的吸引子流形上，即使重构系统与原系统维数相差较大，也可在拓扑关系或微分意义上属同一等价(微分同胚)，具有相同的动力学性质与几何性质，系统的许多特性如分维、K熵、李指数等均相同。

为直观表明旋翼在相空间中的损伤演化过程，将带桨叶损伤BO-105旋翼的桨尖位移及桨毂载荷数据进行相空间重构。相空间重构时，延迟时间与嵌入维数是两主要参数，采用平均互信息法及假近邻法确定［9］，计算流程见图4。求得延迟时间为30，嵌入维数为4，信号相轨迹在三维空间中的投影见图5。由图可直观看出旋翼系统的稳态相轨迹(吸引子)在重构空间中被完全展开，通过相轨迹随桨叶损伤扩展而出现的漂移及变形等几何变化可直观了解与跟踪旋翼损伤演化过程。

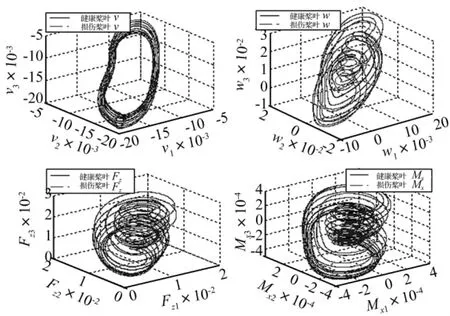
图5 相轨迹在三维空间中的投影Fig.5 3D views of reconstructed phase space trajectories

2 重构相空间跟踪旋翼损伤方法

基于相空间状态预测残差的旋翼损伤跟踪程序(图6)主要包括损伤观测信号生成模块与损伤状态优化估计模块。前者先据健康旋翼在相空间内的运动轨迹采用Volterra预测器［10］建立基准旋翼短时状态预测模型，系统运行时用现场采集数据及Volterra预测器估计基准状态，与实测状态之间的差异即短时状态预测残差，对一条记录内的残差进行统计、组合可形成残差特征向量。而后者将生成的残差特征向量代入观测方程得到桨叶损伤观测值，用桨叶损伤演化方程计算Unscented变换［11］，产生西格玛点及其权重与状态转移点，调用预测步计算损伤变量均值及方差的一步估计;调用修正步估计观测变量均值、方差，计算增益矩阵并修正损伤变量的均值估计与方差。

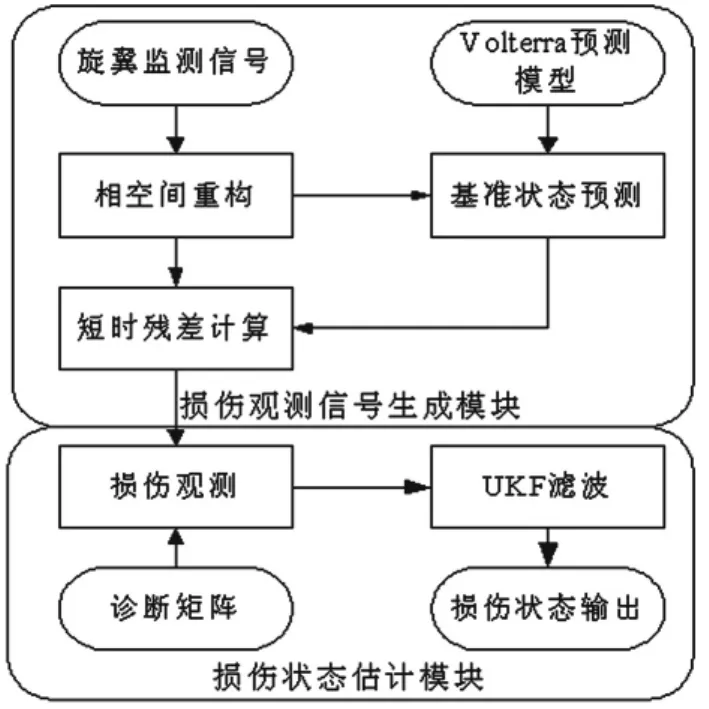
图6 旋翼损伤跟踪程序原理图Fig.6 Rotor damage tracking system framework

2.1 损伤观测信号生成

在旋翼系统状态空间中，可用损伤旋翼与健康旋翼轨迹之间的短时偏差作为系统损伤观测信号。设旋翼在某任意时刻状态为xn，损伤为φ，经过短时间τ后旋翼状态变为x(xn，τ，φ)。若按健康系统(φ=φR)估计其状态则应为x(xn，τ，φR)，两状态之间的残差为:

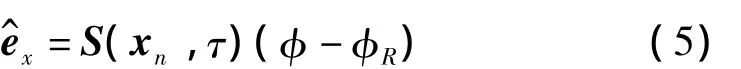
它在xn，τ一定条件下对损伤具有近似线性可观性。

其中:

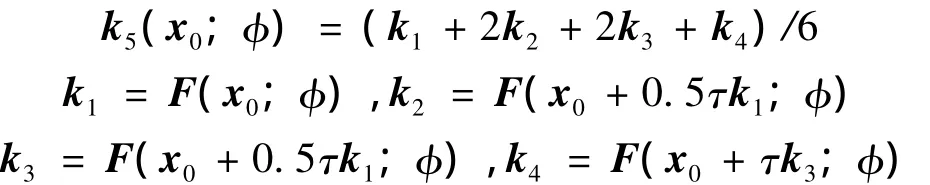
用式(5)计算出短时状态残差后，即可研究灵敏度S(xn，τ)随系统初始状态及损伤大小的变化情况，具体分析高阶小量影响。

分析实例旋翼桨尖挥舞位移的短时残差灵敏度随初始状态和桨叶刚度损伤的变化情况。在健康旋翼的状态空间中随机选择16个点作为计算初始状态，在桨叶寿命周期(0≤t/tF＜1)内等间隔取60个时间点，用式(5)计算出旋翼桨叶挥舞位移的短时状态残差随使用寿命和桨叶损伤大小的变化曲线见图7。左图中16条桨尖挥舞位移的短时残差ew的曲线对应于16个初始状态，在初始状态一定的情况下，桨尖位移的短时残差是损伤变量的光滑连续函数，且与桨叶损伤演化曲线非常一致。右图表明，短时残差灵敏度只与系统的初始状态有关，而不随损伤的大小有明显变化，如果对多个状态点的短时残差进行平均，则可以得到一种相对于系统状态和损伤都有比较稳定灵敏度的损伤观测信号。

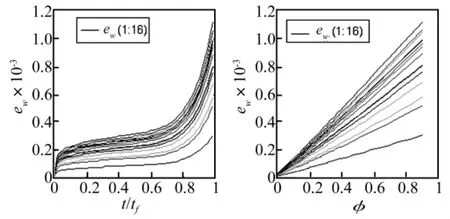
图7 短时状态残差与寿命(左)和损伤(右)的关系Fig.7 Curves of short time state error vs.life time(left)and damage variable(right)

表面上，有了旋翼气弹有限元模型即可计算x(xn，τ，φR)，但该方法在计算短时状态残差时要求能直接测量旋翼气弹有限元模型中的全部状态量，需实时采集许多节点处的桨叶位移数据，这在实际应用中较难进行。考虑到原物理系统在一定意义下与相空间中的重构系统存在某种拓扑等价关系，则可在基准相空间中利用基准状态预测模型生成新的状态残差ex，作为物理空间中状态残差e^x的替代，即，据健康旋翼在相空间内的运动轨迹，用非线性Volterra级数建立基准旋翼短时状态预测模型。监测时将旋翼状态采集数据运用延迟嵌入方法重构出实测相轨迹，并采用Volterra预测模型算出参考轨迹，并将其与实测相轨迹之间的差异统计平均生成损伤观测信号。由于传感器测量误差、Volterra预测模型在不同区域内的精度变化、灵敏度在相轨迹上的起伏误差等随机干扰影响，单个短时状态残差具有较大不确定性。为提高损伤检测的鲁棒性，用一条记录内所有残差的平均值ek作为损伤观测特征向量。基于Volterra预测模型的损伤观测信号生成方法为:

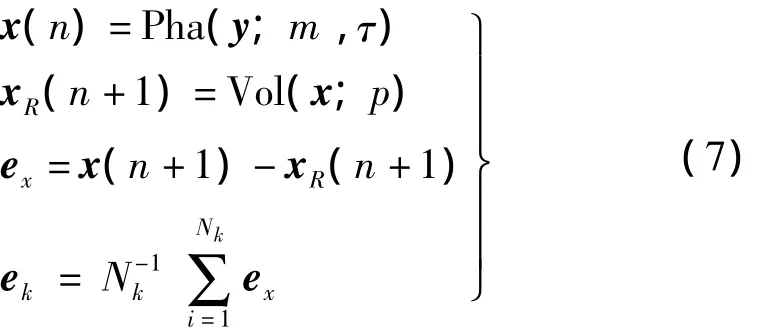
其中:y为传感器输出序列;Pha为相空间重构算子;m，τ分别为嵌入维数及时延参数;x为相点;xR为预测器输出参考点;ex为状态预测残差;ek为残差均值(损伤观测信号);Nk为记录长度;Vol为Volterra预测器;p为预测器阶数。P阶截断及形式的Volterra预测器可表示为:

式中:

其中:hp(i1，…，ip)为p阶Volterra核;X(n)为预测器输入信号矩阵;w为预测器系数向量，可据健康旋翼的相轨迹用NLMS自适应算法［11］确定:

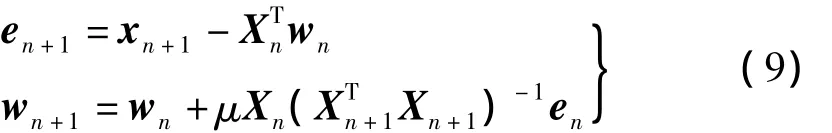
式中:μ为收敛控制参数(0＜μ＜2)。

图8 损伤观测信号计算流程Fig.8 Flow chart of damage measurement prediction

为说明采用Volterra预测模型生成损伤观测信号方法的有效性，用损伤观测信号生成程序(图8)对实例旋翼在不同损伤状态下的桨叶位移及桨毂载荷进行分析。在桨叶寿命周期内(0≤t/tF＜1)，等时间间隔采集60个损伤程度(0≤φ＜1)下的仿真记录，计算得到各记录残差均值随使用寿命的变化如图9所示。与图1对比可见，各残差均值分量与桨叶损伤变量的变化趋势较一致，说明残差主要来自桨叶损伤的变化而非模型计算误差。对比分析残差均值和桨叶损伤之间的对应关系，容易验证两者有较显著的线性关系。

图9 残差均值向量随时间的变化Fig.9 Curves of residual tracking metric

2.2 桨叶损伤估计

旋翼系统偏离正常状态时，残差均值ek可近似线性反映出桨叶的损伤程度。设由残差均值到桨叶损伤的线性观测方程为:

其中:yk为桨叶损伤第k次观测值，H1为诊断矩阵，h2为常数项。设得到关于桨叶损伤及残差均值的实验样本，则系数H1，h2可确定方法为:

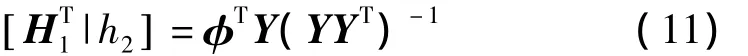
式中:

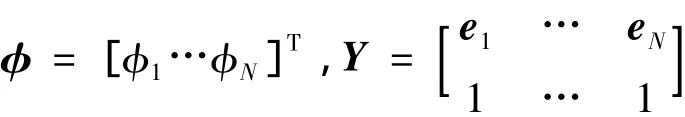
由于传感器测量误差、Volterra预测模型在不同区域内的精度变化、灵敏度在相轨迹上的起伏误差等随机干扰影响，由式(9)确定的损伤观测中通常仍有较大起伏，桨叶损伤状态的估计在技术实质上是一种优化滤波的过程。考虑到损伤演化过程(式(2))的非线性，本文选择Unscented滤波器对损伤观测数据处理。与传统滤波器(如扩展Kalman滤波器)相比，该滤波器采用Unscented变换通过2n+1个西格玛点及状态转移点的联合分布对状态变量进行估计，可较好反映非线性状态转移函数中的高阶距成分，降低分析误差［11］。Unscented滤波器主要含预测步和修正步，预测步用于计算损伤变量均值及方差的一步估计值，计算式为:

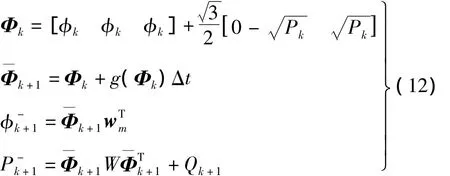
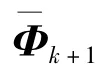
修正步用于估计观测变量均值及方差，并用观测结果修正损伤变量的均值及方差，计算式为:

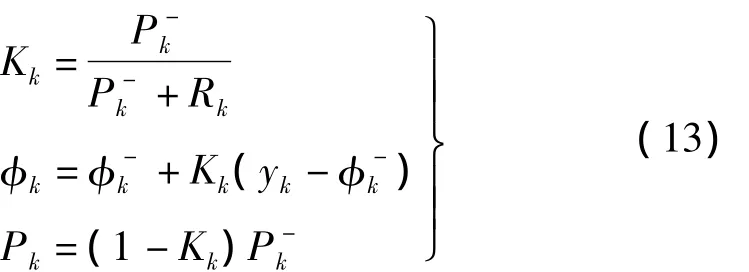
式中:Kk为滤波增益;Rk为观测噪声方差。

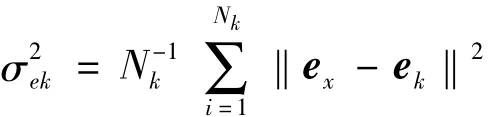
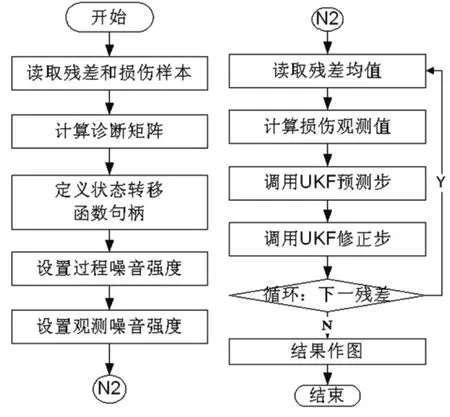
图10 采用UKF滤波器估计桨叶损伤流程Fig.10 Flowchart to estimate blade damage using Unscented Filter

图11 桨尖挥舞位移对损伤的估计Fig.11 Tracking results of damage using blade flaps

3 结论

本文用信号重构技术与Volterra预测模型提出新的损伤观测信号生成方法，该方法利用信号的非线性特性在更高维数的状态空间内重构旋翼系统的动力学本质，并运用现代滤波技术在飞行状态下跟踪旋翼的损伤状况，克服了旋翼可测状态变量数目的限制问题。对结构损伤机理和材料失效理论的研究通常在微观尺度上进行。但此研究不能阐明损伤过程在整个系统宏观行为中的表现，不能提供系统级损伤跟踪手段。而源自混沌分析理论的相空间重构技术，可从不同时空角度观察系统损伤行为特性。研究表明，只要时间尺度及空间维数选择合适，即可通过相轨迹光滑移动了解损伤的累积过程。

［1］ Azzam H，Andrew M J.The use of math-dynamic model to aid the development of integrated health and usage monitoring［J］.Journal of Aerospace Engineering，1992，206(1):71-96.

［2］ Ganguli R，Chopra I，Haas D J.Detection of helicopter rotor system simulated faults using neural networks［J］.Journal of American Helicopter Soc，1997，42(2):161-171.

［3］Pawar P M，Ganguli R.Fuzzy logic based health monitoring and residual life prediction for composite rotor［J］.Journal of Aircraft，2007，44(3):981-995.

［4］Pawar P M，Ganguli R.Helicopter rotor health monitoring-a review［J］.Journal of Aerospace Engineering，2007，221(1):631-647.

［5］Johnson W.Comprehensive analytical model for rotorcraft aerodynamics and dynamics volumes ii:components theory［M］.California:Johnson Aeronautics，Palo Alto，2007:280-283.

［6］ Miles T J，Lucas M.Torsional and bending vibration measurements on rotors using laser technology［J］.J.Sound Vibr.，1999，266(3):1441-1467.

［7］Pawar P M，Ganguli R.On the effect of progressive damage on composite helicopter rotor system behavior［J］.Composite Structures，2007，78(3):410-423.

［8］ Robert C H.Chaos and nonlinear dynamics［M］.Oxford University Press，2002.

［9］陈 果.非线性时间序列的动力学混沌特征自动提取技术［J］.航空动力学报，2007，22(1):1-6.CHEN Guo.Dynamic chaos features auto extracting technique of nonlinear time series［J］.Journal of Aerospace Power，2007，22(1):1-6.

［10］张家树，肖先赐.混沌时间序列的 Volterra自适应预测［J］.物理学报，2000，49(3):404-408.

ZHANG Jia-shu，XIAO Xian-ci.Predicting low dimensional chaotic time series using volterra adaptive filer［J］.Acta Physic Asinic，2000，49(3):404-408.

［11］ Julier S J，Uhlmann J K.Unscented filtering and nonlinear estimation［J］.Proc.IEEE，2004，92(3):401-422.

［12］ Chelidze D，Liu M.Dynamical systems approach to fatigue damage identification［J］.J Sound and Vibration，2005，281(3):887-904.