轴流压气机旋转失速和喘振的非线性反馈控制

陈 振，徐 鉴

(同济大学 航空航天与力学学院，上海 200092)

近些年学者对压气机的研究产生了很大的兴趣，这其中主要包括对压气机内部气流的动力学行为的研究以及旋转失速和喘振的控制问题［1-3］。出现这股研究热潮的原因是因为近些年压气机工业上越来越追求大的升压比和大推力的压气机。当轴流压气机工作在最大压升时，容易产生不稳定的工作状态，即压气机容易进入到旋转失速和喘振工况。压气机进入到旋转失速和喘振后，飞机发动机会出现不稳定的振动，从而导致飞机出现“颤抖”，甚至会出现机毁人亡的惨剧。因此避免这两种不稳定的工作形式的出现具有很重要的意义。学者们把目光集中在了主动的采取措施来控制压气机的动力学行为，保证压气机不会进入到旋转失速或者喘振。

上个世纪80年代，学者Moore等［4］提出了一个把压缩系统流量、压升、扰动波振幅耦合到一起的非线性动力学模型。这个模型形式上很简单，但实验发现它能够准确的预测到旋转失速和喘振的发生［5］。基于MG模型的优越性，在过去的几十年里，很多学者以MG模型为基本模型，提出了对轴流压气机旋转失速和喘振的控制策略［6］。需要看到的是很多控制策略都是独立的针对旋转失速或喘振来控制。但是旋转失速是喘振的先兆，旋转失速和喘振之间没有明确的分界线，因此需要把这两种不稳定的形式统一起来进行研究。Gu等［7］提出来的控制策略，初步的弥补了以前的控制策略的缺点，能够控制旋转失速和喘振的发生。旋转失速在失速点附近发生叉式分岔，通过对线性化系统的分析，我们知道线性反馈控制对于系统的零特征根没有影响，因此需要采用非线性控制策略［8］。Wang等［9］的研究表明，对于以节流阀作为执行机构(actuator)的线性控制策略，在消除旋转失速所伴随出现的迟回现象时会失效。因此非线性控制就成了学者研究的重点领域。而对喘振的控制主要是增加压气机的喘振裕度，避免压气机进入到喘振这种极端的工况。

本文是介绍了一种简单有效的控制策略，可以对工程上进行压气机不稳定工作的控制提供参考。

1 模型和旋转失速现象

1986年，Moore和Greitzer建立的耦合非线性动力学 MG 模型［4］为:

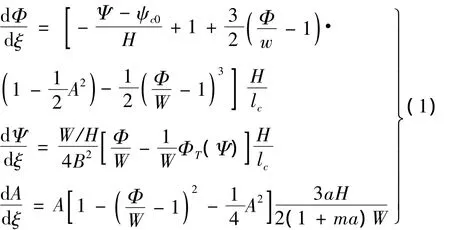
其中:Φ为无量纲的流量系数，Ψ为无量纲的压升系数，B为Greiter参数，lc为管道平均长度，a为时间参数，r为节流参数，A为流量波动的一次谐波振幅，W、H为和压气机有关的常数，ΦT(Ψ)为节流特性函数。根据实际的工况［7］，本文中的参数取值为:lc=3，ψc0=0.3，H=0.18，W=0.25，r=0.4，B=0.4。

当压气机进气量减小时，压气机的内部气流会出现一个周向旋转的扰动波，这个扰动波的存在会在叶片前段造成堵塞，增加气流攻角，从而产生气流分离，压气机进入到旋转失速状态。旋转失速进一步发展，压气机内气流会出现全流程的大振幅的轴向振动，进入到喘振状态，此时周向扰动消失，方程(1)中A会变为零。进一步，A=0为喘振的必要条件，为了研究在此情况下参数r和B对喘振的影响，首先简化方程(1)，为此，作变换:

为记号方便，去掉上述记号上的波浪号，仍把流量系数记为Φ，节流阀参数为r，流量系数的一次谐波振幅为A。将上述记号带入方程(1)有:

其中:

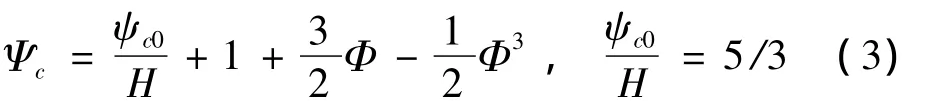
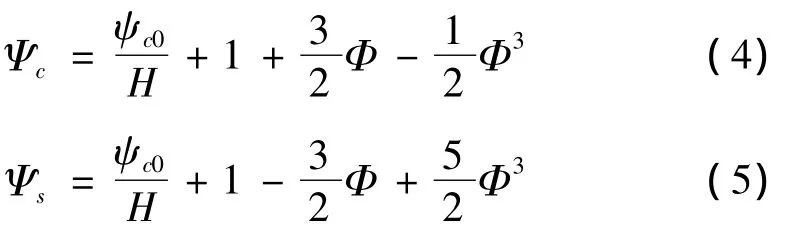
压气机稳定工作点由压压升特性Ψc以及节流特性的交点的位置来决定，方程(1)中压气机的节流特性表示为:

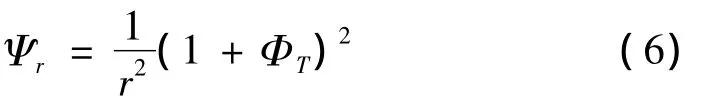
由方程(4)、(5)、(6)可以得到压气机的特性曲线，如图1。

图1 压气机特性曲线Fig.1 Schematic of compressor characteristic

图1中rc和ra分别对应着节流线Ψr与Ψc交点位于最高点1处以及与曲线Ψs相切时对应的节流参数值。本文中可以根据方程(4)、(5)和(6)求得rc=1.034，ra=1.096。下一节的稳定性分析可以得到曲线Ψc和Ψs的虚线部分代表着系统(2)的不稳定的平衡点，而实线部分代表稳定的平衡点。于是，压气机稳定工作时，节流线和稳态特性线的交点4位于稳态特性线右支，为稳定状态。此时减小节流参数r，节流线向左侧偏移，交点向上移动，压升系数增加，压气机的效率增加。当到达最高点1时，压气机的效率达到最大值。继续减小节流参数r，交点将进入到旋转失速不稳定区域，交点会从1点跳跃到非轴对称压升特性线上的2点，处在一个稳定状态，而不是沿着轴对称曲线向左移动。为了使压气机从旋转失速退出，需要增加节流阀参数r的值，但是此时交点不会沿着原路跳回到最高点1点，而是会沿着Φs曲线继续向下移动到3点，压气机的效率继续减小。随着节流参数进一步的增加，交点会从3跳跃到稳定的区域上的交点4。以上描述的节流线与特性线的交点的运动路径为4→1→2→3→4，构成了旋转失速所伴随的迟回环。迟回环的存在会使压气机旋转失速的控制伴随着降低压气机效率的现象，因此需要采取有效的控制策略来消除迟回环的存在。

2 旋转失速控制

上面提到了由于旋转失速时伴随着迟回现象，这个现象的存在对于旋转失速的控制带来了很大的麻烦，因此需要提出能够消除迟回现象的控制策略。而在非线性动力学理论中提到亚临界的叉形分岔会导致迟回环的存在，而超临界的叉形分岔则不会产生迟回环。因此构造控制策略的出发点就是控制能够使系统在分岔点附近的分岔由亚临界的叉形分岔变为超临界的叉形分岔［11］。

下面我们采用基于在失速点附近调整节流阀参数的方法来提出对应的反馈控制策略。系统(2)可以写为:

其中u为非线性的反馈控制函数:

Ψ0是对应着预先设定的压气机稳定时的压气机的压升值，本文中取Ψ0=0.6。我们的目的是使这个控制策略能够消除旋转失速伴随的迟回现象。同时需要指出的是，k＞0、u＞0、r＞0，这样反馈控制实际上通过增加节流参数来进行旋转失速的控制。为了得到控制系统的平衡态，令方程(7)右端等于零得到:

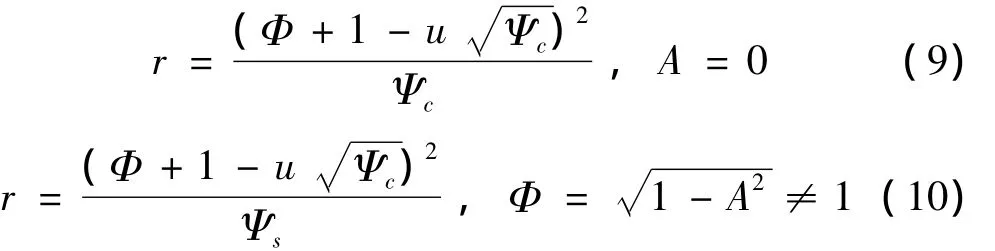
其中u=ksin(Ψ-Ψ0)，首先讨论k=0时，这时有未施加控制的情形。

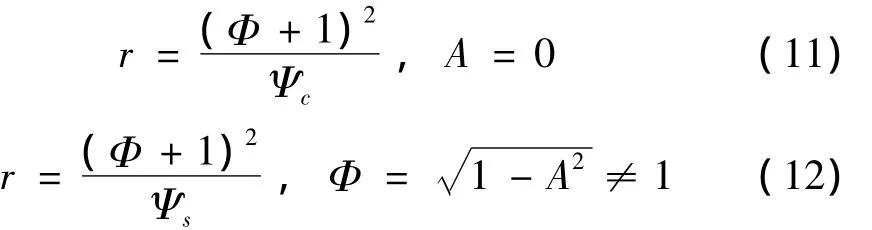
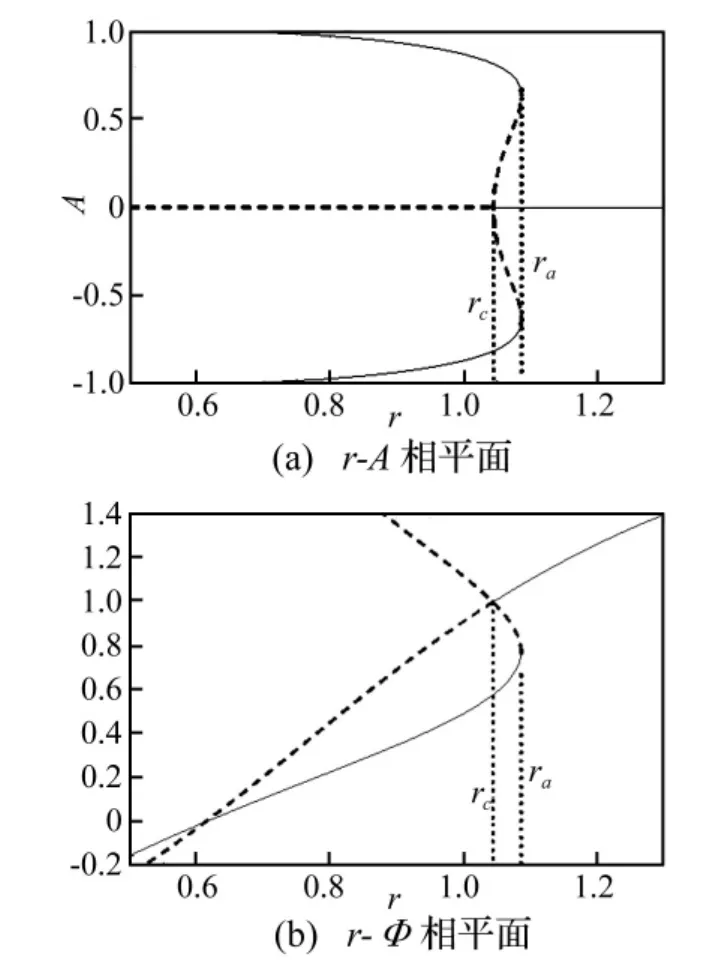
图2 k=0时系统(2)的平衡态(11)和(12)随r的变化情况Fig.2 The stable steady(11)and(12)for k=0 with r varying in system(2)

未施加控制的系统(2)的分岔图如图2所示，图2由方程(11)、(12)得到。从图2(a)中可以看出，r＜rc时，有不稳定的平衡点A=0及两个稳定的非零平衡点，可以由系统(2)线性分析得到的雅克比矩阵的特征根的实部的正负来判断;ra＞r＞rc时，有稳定的平衡点0和两个非零的稳定的平衡点及两个非零的不稳定平衡点;当r＞ra时有稳定的平衡点A=0。系统(2)在r=rc处发生亚临界的叉形分岔，r＜rc系统的平衡点不稳定，对应着图1中曲线Ψc的左支不稳定，而右支是稳定的。图2(b)中看出，r=ra时，系统(2)发生鞍结分岔。ra＞r＞rc时，出现两个平衡点，分别对应着流量较大的分支和流量较小的分支，其中流量大的分支不稳定，而流量小的分支稳定，对应着图1中Ψs的上支不稳定，而下支稳定［10］。

从图2中可以看出，没有加入反馈控制的系统会随着节流参数的减小，在分岔点r=rc处发生亚临界的叉形分岔，系统(2)会出现迟回现象。图2中下图得，增加压气机的节流参数值，系统(2)的平衡点会在r=rs处发生跳跃现象。即增加节流参数值，平衡点不能够沿着原来的路径返回到稳态特性线上，表现为旋转失速时的迟回现象。

对于控制系统(7)和(8)结合(9)和(10)得到分岔图3和4，其中控制参数分别为分别对应着k=0.06和k=0.2。在图3中，取定控制参数k=0.06，系统在分岔点r=rc附近发生超临界的叉形分岔，迟回现象消失。此时系统(7)的平衡点在r=rs处的跳跃现象消失，因此能够通过控制实现消去旋转失速迟回现象的目的。增大控制参数，k=0.2，压气机会从旋转失速曲线上更加平稳的过渡到轴对称曲线上，旋转失速的控制会更加的顺利，如图4所示。

需要提及的是，在对压气机节流阀参数来实施反馈控制时，添加的反馈信号值不应该过大，否则会使压气机的节流特性发生大的变化，从而使压气机内部气流的流动受到过大的影响。

图3 k=0.06时系统(7)的平衡态(9)和(10)随r的变化情况Fig.3 The stable steady(9)and(10)for k=0.06 with r varying in system(7)

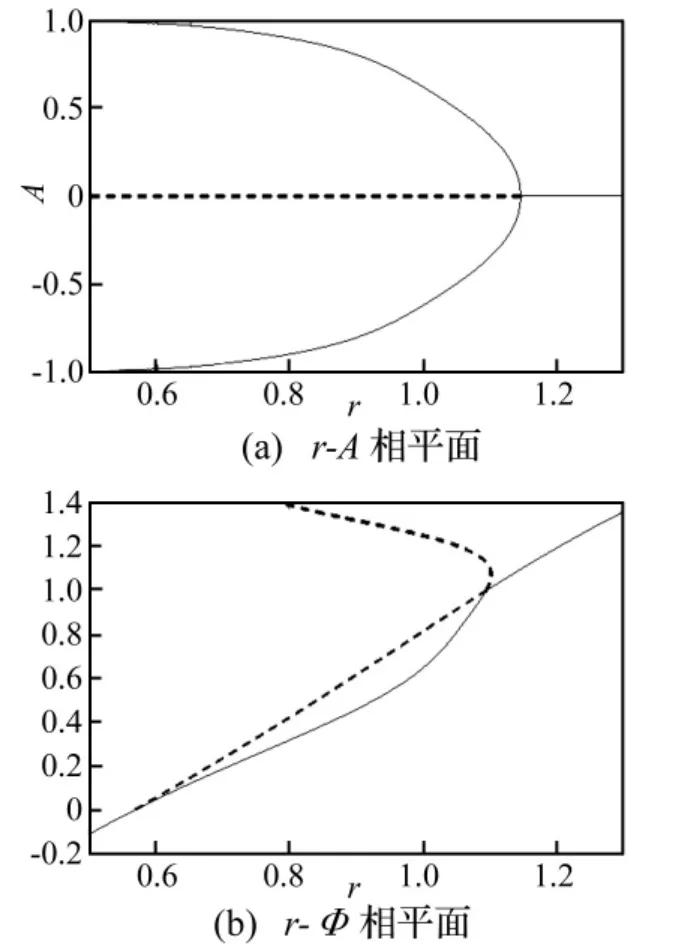
图4 k=0.2时时系统(7)的平衡态(9)和(10)随r的变化情况Fig.4 The stable steady(9)and(10)for k=0.2 with r varying in system(7)

3 喘振现象控制

当压气机处于喘振状态时，内部的气流为轴向往复振荡，周向失速气流团消失，对应着Ae=0的情形［4］。为了更好的说明喘振控制时真实的压气机压升和流量的变化情况，本文采用未简化的系统模型。喘振控制系统模型转变为:

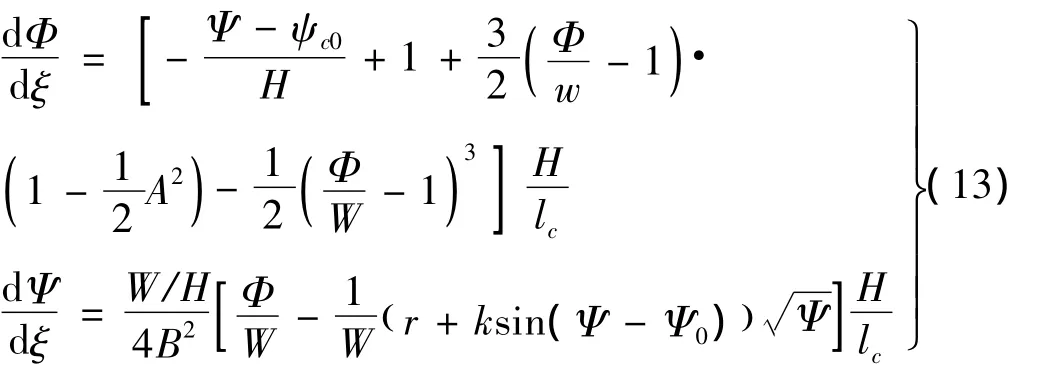
对于没有加入控制的模型(k=0)，系统的动力学行为主要受到节流参数r，以及Greitzer参数的影响。当节流阀参数减小，节流线和稳态特性线的交点越过最高点进入到左支时，压气机的稳态特性将会发生改变而进入到不稳定的状态对应着旋转失速的情况，而此时系统是否会进入到喘振状况，还需要由Greitzer参数值的大小来确定。系统中存在一个临界的Greitzer参数Bc，当B＞Bc时，压气机会进入到喘振状态。而B＜Bc时，压气机则处在旋转失速状态［4］。压气机一旦进入到喘振状态，则会在内部出现周期性的往复振动，对应着动力系统出现周期振动的情形［12］。这种振动是大振幅、低频率的振动，对压气机的安全工作危害很大，是压气机工作中需要避免出现的情况。

压气机的喘振对应着非线性动力学系统中出现了周期振动。因此加入控制的动力学系统中，就需要研究随控制参数k的变化，期望系统会发生亚临界Hopf分岔，平衡态从周期运动变为稳定的焦点。

假定控制系统的平衡点为(Φ0，Ψ0)，作变换~Φ=Φ-Φ0，~Ψ=Ψ-Ψ0将系统的平衡点移动到(0，0)，为便于书写记忆，仍把流量系数和压升系数记为Φ、Ψ。可以得到对应的平衡点位于(0，0)的控制系统的线性化方程为:

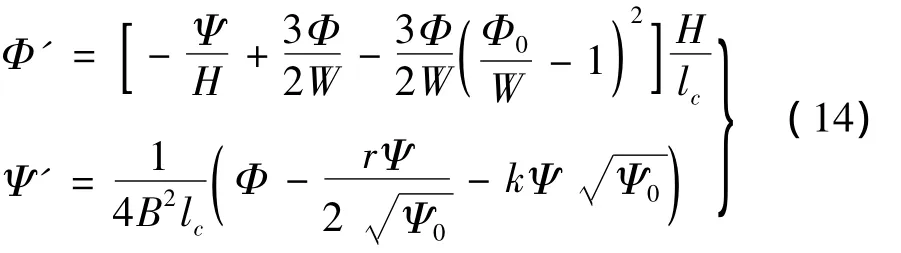
线性化系统(14)对应的特征方程为:

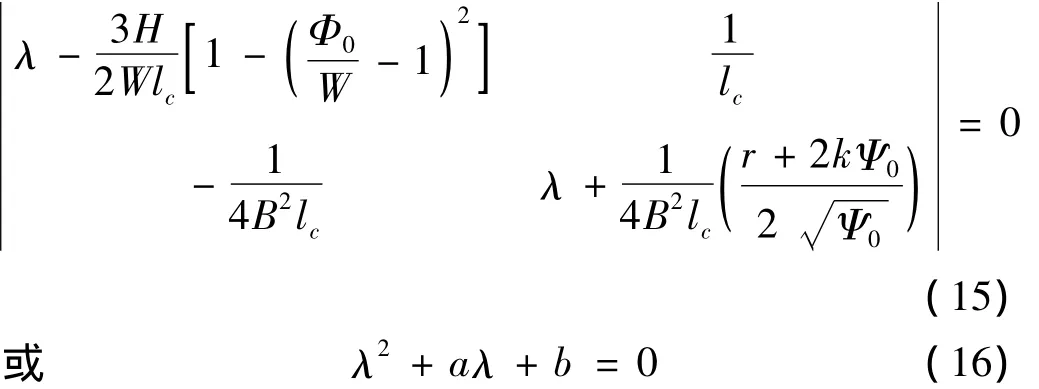
其中:

假定系统特征方程存在一对纯虚根λ=±ωi，其中ω为振动频率，代入到特征方程(16):

为了保证上式恒成立，要求实部虚步都为零，从而满足下列条件:

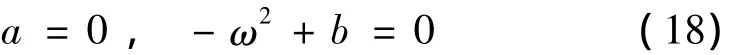
因此可求得系统发生Hopf分岔时的临界控制参数的值:

通过Winpp软件来进行数值仿真，得到控制系统(14)的Hopf分岔图，如图5所示，其中分岔参数为k。根据图5知，控制系统存在一个临界的控制参数kc，当k＜kc时，控制系统会出现极限环，进入到周期振动，对应着压气机中出现喘振状态;k＞kc时，控制系统的平衡点为稳定焦点，压气机从喘振状态退出。

图 5 lc=3，H=0.15，W=0.25 时，控制系统(14)对应的Hopf分岔图Fig.5 lc=3，H=0.15，W=0.25，Hopf bifurcation diagram of controlled system(14)

图6和7是对系统(13)进行数值仿真得到的压升的时间历程图。从图6中可以看出，当控制参数k=0.5时，控制系统(13)的压升将进入周期振动，表现为压气机进入到喘振工况。而当控制参数k=0.6时，系统(13)的压升会趋向于稳定，而不是周期振动，此时压气机从喘振状况退出，压气机的压升将维持在一个定值。

为了验证控制系统策略对喘振的控制效果，根据系统(13)得到了图8，其中实线代表着k=0未施加控制时，压升随时间的变化曲线，而虚线代表施加控制后的压升变化。图8(a)中可以看出此时压气机处在喘振状态，压升的变化满足周期振动规律，未施加控制的系统振动的振幅为0.35，而施加控制后，取控制参数k=0.52时，系统压升变化的幅度明显减小，为0.2左右。而当继续增大控制参数至k=0.58时，系统压升的周期振动将会完全的抑制下来，达到了控制的目的。

图 6 lc=3，ψc0=0.3，H=0.18，W=0.25，r=0.4，B=0.4，k=0.5 时，控制系统(13)的压升时间历程图和相图Fig.6 Transient controlled system(13)behavior:lc=3，ψc0=0.3，H=0.18，W=0.25，r=0.4，B=0.4，k=0.5

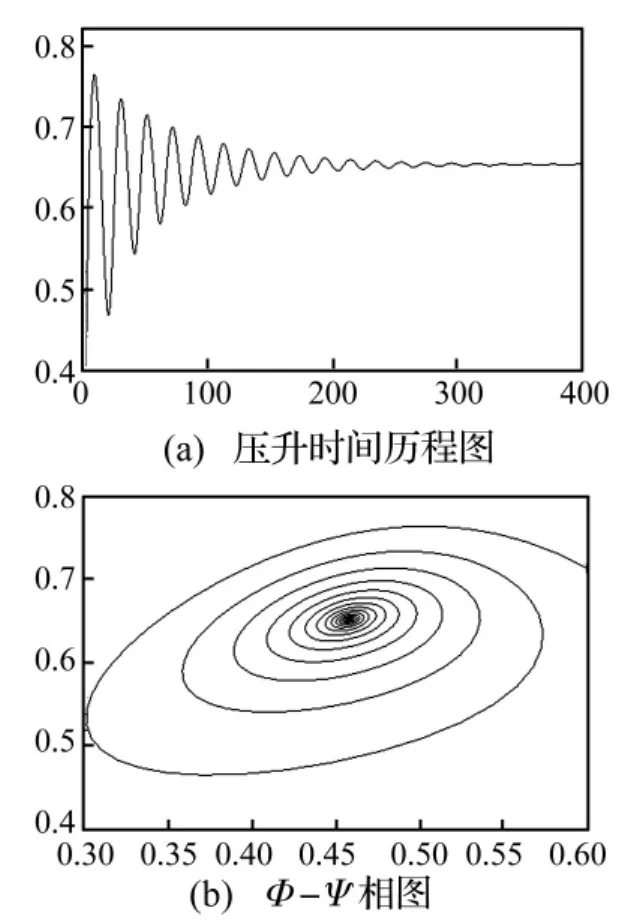
图 7 lc=3，ψc0=0.3，H=0.18，W=0.25，r=0.4，B=0.4，k=0.6 时，控制系统(13)的压升时间历程和相图Fig.7 Transient controlled system(13)behavior:lc=3，ψc0=0.3，H=0.18，W=0.25，r=0.4，B=0.4，k=0.6

图8 lc=3，ψc0=0.3，H=0.18，W=0.25，r=0.4，B=0.4 时系统(13)的控制效果图(虚线为施加控制的效果，黑实线为未施加控制)Fig.8 Control effect diagram(13)(Dotted line is vibration curve with control，solid line is without control)，lc=3，ψc0=0.3，H=0.18，W=0.25，r=0.4，B=0.4

值得指出的是，本文当压气机稳定时压升值不大，压气机回到理想的工作状态还需要重新对气体进行加压。但是可以避免压气机进入喘振这种危害很大的工作状态。

图9表明了控制系统(14)对于不同的控制参数，节流参数r和临界Greitzer参数B的关系。图中的曲线为喘振边界线，曲线以上的部分代表着会出现喘振的区域，曲线下方则代表着稳定的区域。从图中可以看到，随着控制参数的增加，对于不同得节流参数值，出现喘振时对应的GreitzerB参数的值会增加，喘振边界曲线以上的面积会逐渐的减小，表明着喘振区域减小，而稳定的区域增大，从而增加了压气机的稳定工作范围。

4 结论

图 9 lc=3，ψc0=0.3，H=0.18，W=0.25不同的控制参数k值，对应的B-r图Fig.9 B-r dragram for different k:lc=3，ψc0=0.3，H=0.18，W=0.25

由于旋转失速进一步恶化会造成喘振的发生，这两个不稳定的现象并不是独立的，而是有一定联系的，本文应用非线性动力学理论建立了两者之间的关系。旋转失速的控制主要是为了消除迟回效应，使压气机压升随节流参数的增加能平缓的回到轴对称特性线的最高点，且控制策略不能过多的影响节流阀的特性。文中提出的正弦控制策略能够解决这两个问题。而喘振的控制需要压气机进入到喘振这种危害极大的工作状态中。文中提出的正弦控制策略具有以下优点:①能够消除旋转失速的迟回现象，保证压气机能从旋转失速平缓的退出，且控制参数对节流阀特性影响小。② 能够抑制喘振现象的产生，通过增加控制参数能够使动力学系统的解从喘振周期解退出到稳定焦点。

值得指出的是压气机旋转失速与喘振是一复杂的流动失稳情况，主要是叶片边界层流动分离、管网不匹配等流动行为引起的，表现出压力、流量的大幅脉动，是一分布参数的动力学问题，而M-G模型只是一种简化的集中参数模型，用于定性地解释一些现象。

［1］ Bartolini G，Muntoni A，Pisano A，et al.Compressor surge active control via throttle and CCV actuators:A second-ordersliding-mode approach ［C］//IEEE Staff ed.， 2008 International Workshop on Variable Structure Systems.IEEE Conference Publications:Antalya，2008，274-279.

［2］ Chi J N，Paduano J D.New Concepts for active control of rotating stall and surge［C］//IEEE Staff ed.，Proceeding of the 2008 American Control Conference.IEEE Conference Publications:Seattle，2008，2435-2442.

［3 ］ Al-Mawali S，zhang J.Compressor surge control using a variable area throttle and fuzzy logic control［J］.Transaction of the Institute of Measurement and Control，2010，32(4):347-375.

［4］ Moore F K，Greitzer E M.Theory of post-stall transients in axial compression systems:part I-development of equations［J］.ASME Transactions Journal of Engineering for Gas Turbines and Power，1986，108(1):68-76.

［5］Haynes J M，Hendricks G J，Epstein A H.Active stabilization of rotating stall in a three-stage axial compressor［J］.ASME Transactions Journal of Turbomachinery，1994，116(2):226-239.

［6］ Willerms F，Jager B.Modeling and control of rotating stall and surge:an overview［C］//IEEE Staff ed.，Proceedings of the 1998 IEEE InternationalConference on Control Applications.IEEE Conference Publications:Trieste，1998，331-335.

［7］Gu G X，Sparks A G，Banda S S.Bifurcation based nolinear feedback control for rotating stall in axial flow compressors［C］//IEEE Staff ed.Proceedings of the 1997 American Control Conference， IEEE Conference Publications:Albuquerque，1997，1524-1528.

［8］ Liaw D C，Abed H.Active control of compressor stall inception:a Bifurcation-theoretic approach［J］.Automatica，1996，32(1):109-115.

［9］Wang H O，Adomaitis R A，Abed E H.Nonlinear analysis and control of rotating stall in axial flow compressors［C］//IEEE Staff eds.，Proceedings of the 1994 American Control Conference，IEEE Conference Publications:New York，1994，2317-2321.

［10］陈 策，聂超群，李 军.基于三阶MG模型的轴流压气机过失速的非线性分析［J］.应用力学学报，2008，25(3):355-360.

CHEN Ce，NIE Chao-qun，LI Jun.Nonlinear analysis on post-stall transients of axial-flow compressor based on mooregreitzer model［J］.Chinese Journal of Applied Mechanics，2008，25(3):355-360.

［11］ McCaughan F E.Bifurcation analysis of axial flow compressor stability［J］.SIAM Journal of Applied Mathematics，1990，50(5):1232-1253.

［12］ GreitzerE M. Surge and rotating stallin axial-flow compressors I:theoretical compression system model［J］.ASME Transactions Journal of Engineering for Power，1976，98(2):190-198.