不同深度与倾角断层破碎带对Rayleigh波传播及场地地震动反应的影响研究

刘晶波，王文晖，赵冬冬，刘祥庆

(清华大学 土木工程系，北京 100084)

在实际工程中，地震区场地表层和深处经常存在断层破碎带，对场地地震反应造成显著影响［1］。在进行场地地震反应研究时，断层破碎带介质的物理力学性质和几何形态及尺寸等因素都可能对地震反应产生不可忽略的影响［1-3］。

Rayleigh波是一种存在于弹性半空间及成层弹性半空间中由SV波以超临界角入射到弹性半空间表面时产生的转换波。Rayleigh波能量主要分布于半空间自由表面两倍波长范围的薄层内，而且在距离震中较远的场地上，其能量是占优的［4-5］，因此场地地震反应分析时应对Rayleigh波的影响给予足够的重视。

当Rayleigh波在传播过程中通过断层破碎带时将产生反射和透射，对Rayleigh波传播特性及场地地震动反应产生显著影响［6］。一方面，断层对 Rayleigh波有一定的隔震作用;另一方面，断层将加强断层破碎带附近的场地地震反应［7］。

目前国内外在断层破碎带对Rayleigh波传播与场地地震动反应的影响研究成果较少［4-7］。在已有的研究中，文献［6］运用数值模拟方法对Rayleigh波入射情形下的断层效应进行了分析，结果表明断层对Rayleigh波具有隔震作用，且水平向的隔震效果强于竖向。文献［7］通过改变垂直断层破碎带的宽度与剪切波速，研究了垂直断层破碎带的宽度与剪切波速的变化对Rayleigh波传播以及对场地地震动反应的影响。

本文采用 Rayleigh波时域波动输入方法［5］，对Rayleigh波作用下具有不同深度及倾角断层破碎带的场地进行动力时程反应分析，研究断层破碎带深度与倾角的变化对Rayleigh波传播以及对场地地震动反应的影响。

1 计算模型

Rayleigh波入射断层破碎带场地模型如图1所示，设断层破碎带深度为h，与Rayleigh波入射一侧地平面夹角为α，形状取为平行四边形，宽度为6 m，模型边界采用粘弹性人工边界［8-9］。为计算方便，假定半无限空间与断层破碎带介质均为均质、各向同性材料。其中，半无限空间质量密度ρ=2 400 kg/m3，剪切波速cs=1 200 m/s，泊松比ν=0.25;断层破碎带质量密度ρ=2 000 kg/m3，剪切波速cs=120 m/s，泊松比 ν=0.32。

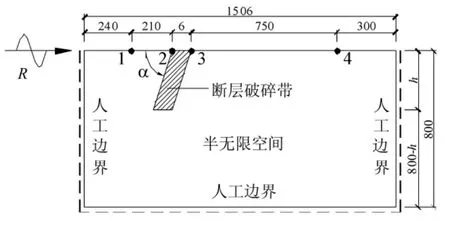
图1 Rayleigh波入射断层破碎带场地模型(单位:m)Fig.1 Model of the fault fracture zone spread by Rayleigh wave(unit:m)

计算模型采用四节点等参单元进行模拟，单元尺寸根据波动有限元模拟的精度要求确定［10］。模型中Rayleigh波由断层左侧场地入射，地震波位移时程如图2所示，位移幅值谱如图3所示。由图3可知，该Rayleigh波的频率主要集中在8 Hz以内，有效最短波长约为138 m。波动输入采用Rayleigh波时域输入方法［5］。采用有限元软件MSC.Marc进行计算时，粘弹性人工边界的实现与Rayleigh波输入采用程序VSBC［11］进行。

2 断层深度变化的影响

为反映断层深度变化的影响，采用垂直断层破碎带进行分析，即取 α=90°。分别取深度h为20 m、40 m、80 m、120 m、160 m 和240 m 进行计算。

图2 入射Rayleigh波的位移时程Fig.2 Time histories of the Rayleigh wave

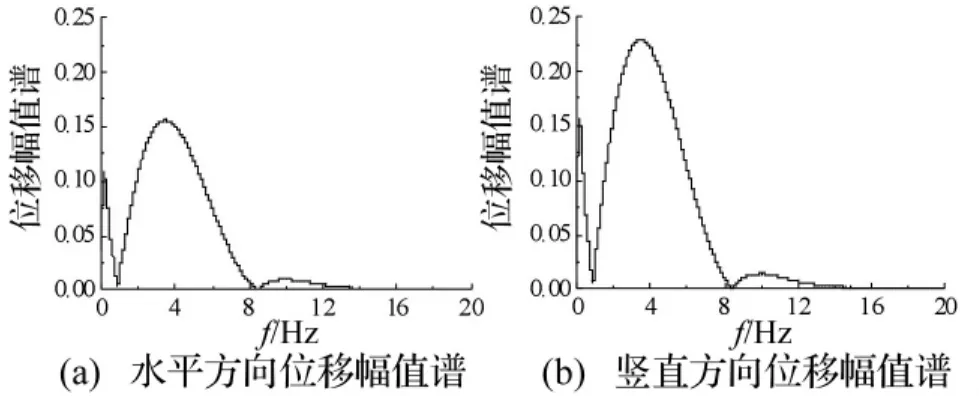
图3 入射Rayleigh波位移幅值谱Fig.3 Displacement amplitude spectrum of the Rayleigh wave

2.1 位移时程计算结果

图4给出了不同断层深度情况下地表的水平与竖向位移峰值，图中水平坐标零点为计算模型的左侧边界点，u和v分别表示水平与竖向位移。由图4可以看到:

(1)在入射波一侧中远场地面处，断层深度对地面峰值位移反应影响很小。

(2)在断层深度较小时(20 m)，场地峰值位移反应基本沿断层中点左右对称，尤其是竖向位移反应。当断层深度由20 m增大到120 m时，入射波一侧的断层角点以及断层左侧距离角点较近处的峰值位移反应均明显增大，但当断层深度进一步增大时逐渐趋于稳定。同时可以看到，随着断层深度的增加，该处水平位移峰值影响区域逐渐变大，而竖向位移峰值影响区域则基本不变。

(3)在断层内部以及右角点处的峰值位移反应规律变化较为复杂，与入射波的频率以及断层破碎带的自振频率等因素有关。

(4)在Rayleigh波越过断层之后，地表水平位移峰值随着距离的增大首先出现一个波峰并逐渐衰减至稳定值;而竖向位移峰值则直接衰减至稳定值。

(5)在断层右侧中远场地面处，峰值位移反应随着断层深度的增加而减小，这说明断层的存在对Rayleigh波的传播具有一定的隔震作用，随着断层深度的增加，这种隔震作用越明显，但当断层深度进一步增大时，该处峰值位移反应逐渐趋于稳定，这与Rayleigh波的能量分布以及断层深度与Rayleigh波长的相对关系有关。另外，水平位移峰值衰减程度略大于竖向位移。

图4 不同断层深度情况地表水平与竖向位移峰值Fig.4 Displacement amplitude of the fault fracture zone with various depths

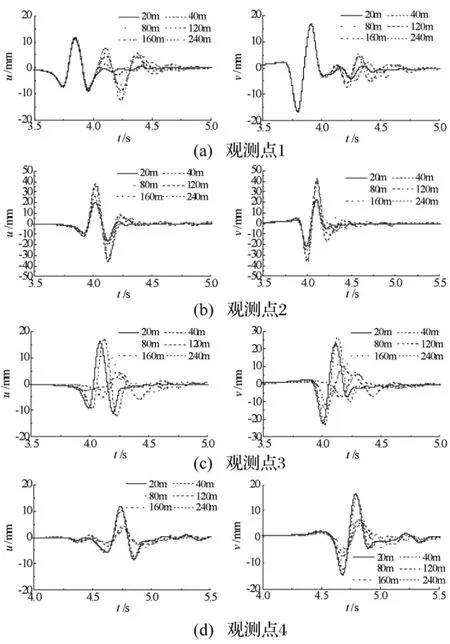
图5 不同观测点水平与竖向位移时程曲线Fig.5 Displacement time histories of the various points

图5给出了不同地表观测点的水平与竖向位移反应时程曲线，地表观测点如图1中所示。由图5也可以看到断层深度变化对不同观测点位移时程的影响规律。

2.2 位移幅值谱比计算结果

图6给出了观测点1-4在不同断层深度情况下的位移幅值谱比［7］计算结果，由于入射Rayleigh波频率主要集中在8 Hz以内，因此在图6中给出了8 Hz以内的计算结果。

图6 不同观测点水平与竖向位移幅值谱比Fig.6 Ratio of displacement amplitude spectrum on various points

由位移幅值谱比的计算结果可以看到:

(1)在入射波一侧的中远场地表面处(观测点1)，位移幅值随着断层深度的增加，在部分频段被放大，而部分被缩小。这主要是因为Rayleigh波在断层界面处发生反射，反射波与入射波发生干涉所引起。

(2)在断层左角点处(观测点2)，随着断层深度的增加，位移幅值在大部分频段内被放大并逐渐趋于稳定，使得该处总体位移反应随着断层深度的增加先逐渐增大，后趋于稳定。

(3)在断层右角点处(观测点3)，随着断层深度的增加，水平与竖向位移幅值在高频段部分被逐渐削弱。

(4)在断层右侧中远场地表面处(观测点4)，随着断层深度的增加，位移幅值在绝大部分频段被逐渐削弱，因此可以推知该点的位移反应随着断层深度的增加而减小，这与位移时程反应计算结果亦是一致的。

3 断层倾角变化的影响

为反映断层倾角变化的影响，采用固定深度的断层破碎带进行分析，取h=60 m。分别取断层倾角α为30°、60°、90°、120°和 150°进行计算。

3.1 位移时程计算结果

图7给出了不同断层倾角情况下地表面的水平与竖向绝对位移峰值，由图7可以看到:

(1)在入射波一侧中远场地表处，断层倾角对该处峰值位移反应影响很小。

(2)在断层左侧距离角点较近处，场地竖向位移反应峰值随着倾角的增大逐渐减小;而场地水平位移反应峰值在倾角为60°时达到最大，随着倾角的进一步增大而逐渐减小。同时可以看到，随着断层倾角的增大，水平与竖向峰值位移影响区域逐渐右移。

(3)对于水平位移反应，倾角为30°时场地峰值出现在断层左侧距断层左角点60 m附近，其他倾角情况下均出现在断层左角点处;对于竖向位移反应，倾角为30°时场地峰值出现在断层左侧距角点30 m附近，倾角为60°和90°时出现在断层左角点处，而倾角为120°和150°时则出现在断层右侧，且随着倾角的增大，场地竖向位移峰值出现点逐渐右移。

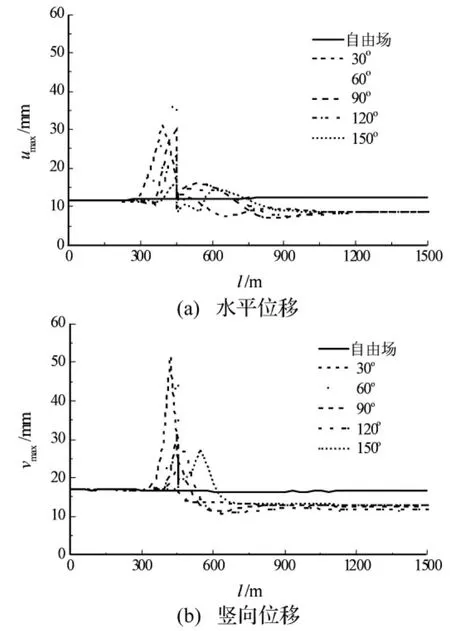
图7 不同断层倾角情况下地表面水平与竖向位移峰值Fig.7 Displacement amplitude of the fault fracture zone with various rake angles

(4)断层右侧中远场地的位移峰值反应在不同断层倾角情况下相差很小，这说明在断层其他参数固定的情况下，断层倾角的变化对Rayleigh波越过断层后另一侧中远场地的位移峰值反应影响很小。

图8给出了观测点2与观测点4的水平与竖向位移反应时程曲线，从中也可以看出观测点位置和断层倾角变化对地面位移反应的影响。

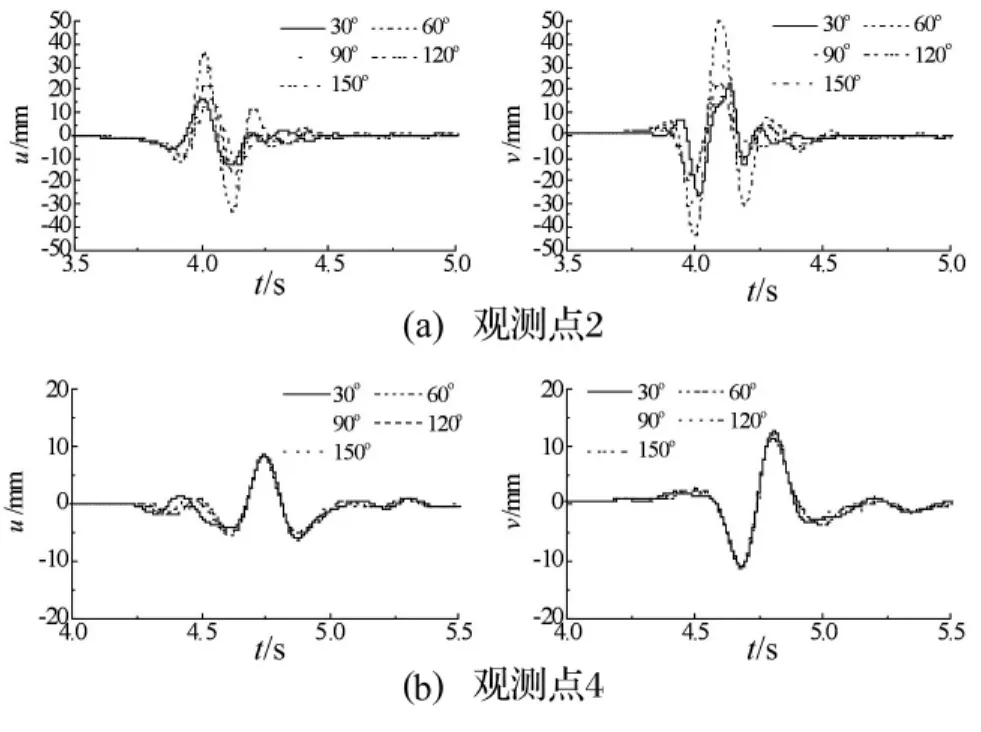
图8 观测点2、4点水平与竖向位移反应时程曲线Fig.8 Displacement time histories of point 2 and point 4

3.2 位移幅值谱比计算结果

图9给出了观测点2、4点在不同断层倾角情况下的位移幅值谱比计算结果。由位移幅值谱比的计算结果可以看到:

(1)在断层左角点处(观测点2)，当断层倾角从30°变化到60°时，位移幅值在所有频段均被放大，当断层倾角从60°变化到150°时，位移幅值在绝大部分频段均逐渐被削弱，这与图8(a)中的位移时程计算结果是一致的。

图9 观测点2、4点水平与竖向位移幅值谱比Fig.9 Ratio of displacement amplitude spectrum on point 2 and point 4

(2)在断层右侧的中远场地处(观测点4)，不同断层倾角情况下的水平与竖向位移谱比均非常接近，且在绝大部分频段小于1。

4 计算结果适用性的分析

上述计算分析是基于坚硬的基岩场地进行的，半无限空间剪切波速取值相对较大，为分析本文计算结果的适用性，本节改变场地及断层破碎带的材料性质进行讨论分析。

以改变断层深度的计算情况为例，计算模型如图10所示，整体模型尺寸为700 m×320 m，输入Rayleigh波如图2所示。半无限空间介质与断层破碎带内介质均设为均质、各向同性，计算参数取为:半无限空间质量密度ρ=2 100 kg/m3，剪切波速cs=500 m/s，泊松比ν=0.25;断层破碎带质量密度ρ=1 700 kg/m3，剪切波速cs=200 m/s，泊松比ν=0.33。取垂直断层破碎带宽度为8 m，分别改变断层破碎带的深度h为20 m、40 m、60 m、80 m和120 m进行计算，图11给出了每种断层深度情况下地表面的水平与竖向绝对位移反应峰值。

图10 Rayleigh波入射断层破碎带场地模型(单位:m)Fig.10 Model of the fault fracture zone spread by Rayleigh wave(unit:m)

由图11可以看到，在Rayleigh波入射一侧的中远场地表，以及断层右侧的中远场地表处，图11表现出来的反应规律与图4基本一致。而在断层破碎带周围较近场地处，由于地震波在该处会发生反射、透射等现象，反应规律相对较为复杂，因此在这些位置的反应现象与2.1节略有不同。

由于入射Rayleigh波的频率主要集中在8 Hz以内，因此可以计算得到入射Rayleigh波在该半无限空间中的有效最短波长约为57 m。由于Rayleigh波的振幅沿竖向按指数规律迅速衰减，因此由图11可以看到，在断层破碎带深度由60 m进一步增大至80 m和120 m时，断层周边的位移反应峰值基本趋于稳定，这与2.1节的结论是一致的。在断层右侧中远场地表，位移反应峰值随断层破碎带深度的增大而减小，同时可以看到，在断层破碎带深度由60m进一步增大时，该处位移反应峰值减小的趋势基本趋于缓和。另外，通过对地表位移幅值谱比的计算分析，可以得到与2.2节基本一致的结论。

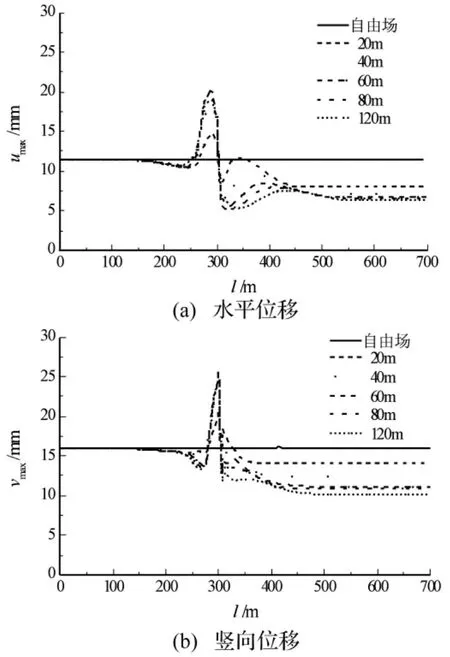
图11 不同断层深度情况地表水平与竖向位移反应峰值Fig.11 Displacement amplitude of the fault fracture zone with various depths

在此种场地条件下，通过改变断层破碎带的倾角得到的结论也和前述计算分析基本一致，此处不再赘述。因此可以看到，本文通过对两种场地条件进行计算分析得到的结论具有较好的一致性，分析结果可以较好地反映断层破碎带深度与倾角的变化对Rayleigh波传播以及对场地地震动反应的影响规律。

5 结论

本文分别对具有不同深度以及不同倾角断层破碎带的场地进行了Rayleigh波作用下的动力时程反应分析，研究了断层破碎带的深度变化与倾角变化对Rayleigh波传播以及对场地地震动反应的影响。

由文中计算结果可以看到，断层存在产生的影响主要体现在两方面:①使Rayleigh波入射一侧断层角点及附近场地的动力反应明显增大;②软弱的断层破碎带对通过的Rayleigh波有衰减削弱作用，使得在Rayleigh波越过断层后另一侧中远场地面的峰值位移反应减小，而断层的存在对Rayleigh波入射一侧中远场地面的影响则很小。

同时可以看到，断层破碎带的深度变化和倾角变化所产生的影响主要表现在以下方面:

(1)在Rayleigh波入射一侧的中远场地表面，断层深度与倾角的变化对地面峰值位移反应影响很小。

(2)在Rayleigh波入射一侧的断层角点以及距角点较近处，地面峰值位移反应随着断层深度的增加而增大，但逐渐趋于稳定;而断层与入射Rayleigh波一侧地面夹角为锐角时的反应则明显大于直角与钝角时的情况。

(3)在Rayleigh波越过断层后另一侧中远场地面的峰值位移反应随着断层深度的增大而减小，且水平位移峰值减小的程度略大于竖向位移峰值;而在其他条件固定的情况下，断层倾角的变化对该处地面的峰值位移反应影响较小。

需要说明的是，上述结论是基于两种场地条件与一种Rayleigh波得到的，对于不同的场地类型以及不同的Rayleigh波，还需要开展更加广泛深入的研究。

［1］李山有，马 强，武东坡，等.断层场地地震反应特征研究［J］.地震工程与工程振动，2003，23(5):32-37.

LI Shan， MA Qiang， WU Dong-po， et al. Study on characteristics of seismic responses of fault sites［J］.Journal of Earthquake Engineering and Engineering Vibration，2003，23(5):32-37.

［2］杨笑梅，王海涛，杨柏坡.竖向断层对场地地面运动的影响［J］.地震工程与工程振动，2006，26(5):7-13.

YANG Xiao-mei， WANG Hai-tao， YANG Bai-po. The influence of vertical cracks in fault sites on the ground motion［J］.Journal of Earthquake Engineering and Engineering Vibration，2006，26(5):7-13.

［3］温瑞智，周正华，孙平善，等.断层场地地震动分析［J］.地震工程与工程振动，2002，22(1):21-27.

WEN Rui-zhi，ZHOU Zheng-hua，SUN Ping-shan，et al.Ground motion analysis for near-fault site［J］.Journal of Earthquake Engineering and Engineering Vibration，2002，22(1):21-27.

［4］Makris N.Soil-pile interaction during the passage of Rayleigh waves:an analytical solution［J］.Earthquake Engineering and Structural Dynamics，1994，23(2):153-167.

［5］刘晶波，李 彬.Rayleigh波作用下地下结构的动力反应分析［J］.工程力学，2006，23(10):132-135.

LIU Jing-bo， LIBin. Dynamic Response analysisof underground structures during propagation of rayleigh waves［J］.Engineering Mechanics，2006，23(10):132-135.

［6］周正华，温瑞智，毛国滨，等.Rayleigh波入射情形下的断层效应［J］.地震工程与工程振动，2006，26(5):1-6.

ZHOU Zheng-hua，WEN Rui-zhi，MAO Guo-bin，et al.Effect of fault on ground motion in the case of incident Rayleigh wave［J］.Journal of Earthquake Engineering and Engineering Vibration，2006，26(5):1-6.

［7］刘晶波，刘祥庆，赵冬冬.垂直断层破碎带对Rayleigh波传播与场地地震动反应的影响研究［J］.爆炸与冲击，2008，28(6):507-514.

LIU Jing-bo，LIU Xiang-qing，Zhao Dongdong.Effects of vertical fault fracture zones on the spreading of Rayleigh wave and ground motion［J］.Explosion and Shock Waves，2008，28(6):507-514.

［8］刘晶波，吕彦东.结构-地基动力相互作用问题分析的一种直接方法［J］.土木工程学报，1998，31(3):55-64.

LIU Jing-bo，LÜ Yan-dong.A direct method for analysis of dynamic soil-structure interaction［J］. China Civil Engineering Journal，1998，31(3):55-64.

［9］刘晶波，李 彬.三维黏弹性静-动力统一人工边界［J］.中国科学(E辑)，2005，35(9):966-980.

LIU Jing-bo，LI Bin.The 3D unified viscous-spring artificial boundary［J］.Science in China Ser.E，2005，35(9):966-980.

［10］廖振鹏.工程波动理论导论［M］.北京:科学出版社，2002.

［11］李 彬，刘晶波.粘弹性人工边界在Marc中的实现［C］//第十四届全国结构工程学术会议论文集第I册.烟台:工程力学杂志社，2005.