模糊聚类算法稳定图应用于桥梁结构参数识别

吴春利 ，刘寒冰 ，王 静

(1.吉林大学 交通学院，长春 130022;2.吉林建筑工程学院，长春 130118)

从桥梁结构上直接监测获得的位移、应变及加速度并不能直接应用于结构损伤识别及状态评估，需要对决定结构动力特性的主要参数(频率、振型和阻尼)进行识别。随机子空间方法是一种有效的广受大家青睐的模态参数识别方法［1-2］。但在随机子空间识别结构模态参数的方法中，确定合理的系统阶次非常重要。选取的系统阶次过少，易遗漏关键模态;反之则易产生虚假模态，因此找到一种方法来确定合理的系统阶次，进而能够准确地识别出结构的动力参数是应用随机子空间法进行模态参数识别的关键。稳定图法由此而生，它是目前常用来确定系统阶次从而识别模态参数最有效的方法。而传统的稳定图进行结构参数识别需要人的主观判断，不能达到自动识别的目的。针对于这一缺陷，本文提出了应用模糊聚类算法绘制稳定图结合随机子空间法进行自动识别结构模态参数的方法。

1 随机子空间法

协方差驱动的随机子空间识别方法(Covariancedriven Stochastic Subspace Identification)是基于随机状态空间模型的性质，通过对输出协方差矩阵进行奇异值分解获得系统矩阵，从而识别系统的模态参数［3-5］。该方法克服了频域方法的不足，不需要FFT变换，避免数据变换引起的截断误差，识别精度高，其基本识别过程如图1所示。

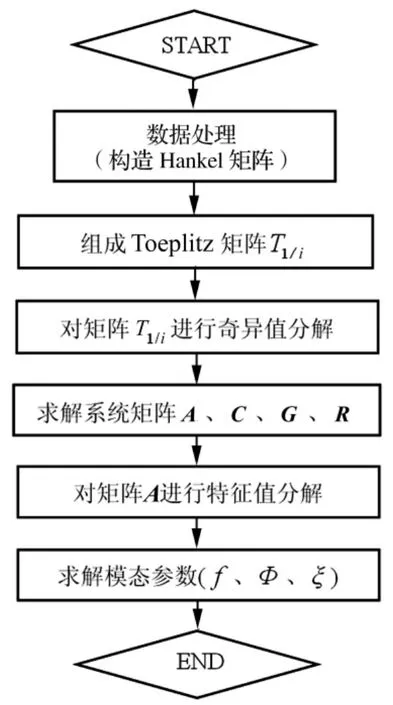
图1 协方差驱动随机子空间法流程图Fig.1 Flow diagram of covariance-driven stochastic subspace identification

2 模糊聚类算法

模糊聚类算法是基于模糊数学的方法，根据客观事物之间的特征、亲疏程度及相似性，通过建立模糊相似关系对客观事物进行分类的一门技术，其内容涉及统计学、生物学及机器学习等研究领域，在模式识别、数据分析和挖掘以及图像处理等领域得到了广泛的应用。

在模糊聚类算法中，最著名和最常用的划分聚类方法是C-均值及其推广模糊C-均值(Fuzzy C-Means，简称为FCM)算法。FCM算法最早是由J.MacQueen提出，由J.C.Bezdek从硬C-均值算法(HCM)推广而来，现已成为最常用和讨论较多的聚类算法之一［6］。其原理是:首先定义一个准则函数即目标函数，随机选择c个初始聚类中心，然后根据样本到聚类中心的距离，划分该样本到该类中;最后再重新计算每个类的聚类中心。上述过程不断重复，直到准则函数达到最小。其描述如下:

令X={xi，i=1，2，…，n}是一训练样本集，X∈Rp，c为预定的分类数量，vi(i=1，2，…，c)是第i个聚类的中心，uik(i=1，2，…，c;k=1，2，…，n)为第k个样本对第i类的隶属度函数，构成的隶属度矩阵U受到以下条件限制:

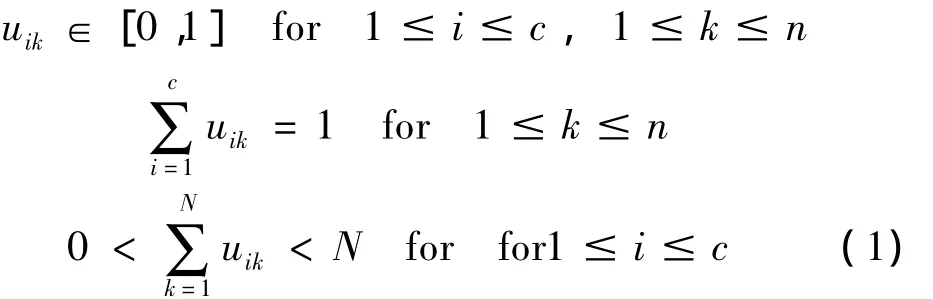
FCM是一种有目标的模糊聚类算法，其目标函数为:

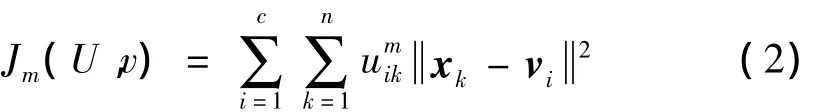
式中，v=(v1，v2，…，vc)，m＞1为模糊参数，该参数决定了聚类的模糊度，也就是数据点可以成为多个类的程度，大多数情况下m=2。当式(2)取到最小值时结果最优。在式(1)的约束下优化(2)可得:

FCM 算法的详细步骤如下:

步骤1 初始化:选择分类数量c、程序终止标准ε＞0以及最大迭代次数T，初始化隶属度矩阵U(0)，使其满足式(1)。令当前迭代数t=1。

步骤2 应用式(4)更新聚类中心v(t):

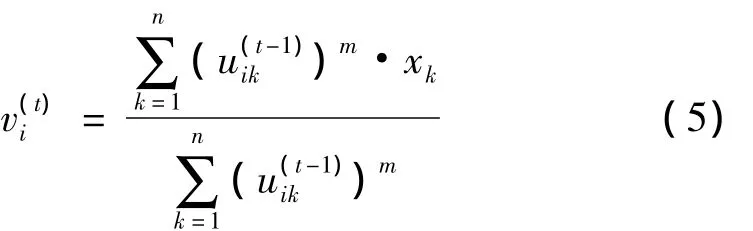
步骤4 由式(3)更新隶属度矩阵U(t):

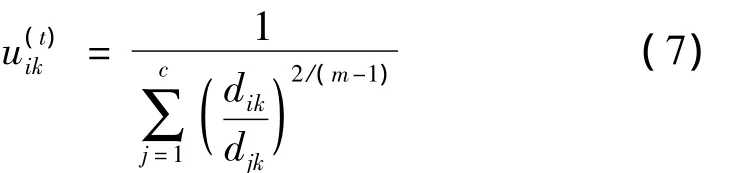
步骤5 终止程序:令t=t+1，重复步骤2，3和4步，直到满足U(t)-U(t-1)或者t＞T。

3 基于模糊聚类算法的稳定图

传统稳定图用于识别系统模态参数需要人的主观判断，需通过有经验的研究人员对极轴进行取舍。由于人的主观参与，容易产生误差，这是用传统稳定图来识别模态参数的最大缺陷［7］。因此，人们采用许多方法对传统的稳定图进行改进，使改进的稳定图更客观更智能，在众多的方法中，基于模糊聚类的稳定图算法是被大家广泛采用且行之有效的方法。目前为止，基于模糊聚类的稳定图均是将数据绘制在以频率为横坐标以阻尼为纵坐标的二维图中，每一类数据点代表了某一阶模态的极点估计［8］。

在实际工程中，相对于频率及振型两个模态参数，阻尼受各种因素的影响存在不稳定性，本文在基于模糊聚类算法的稳定图绘制中以频率为横坐标以MAC中的任一位置数据为纵坐标，使模糊聚类稳定图的每个极点包含两个信息:频率f、模态保证准则(MAC)，选取这两个参数作为聚类因子其限定值可按式(8)进行取值。利用模糊聚类算法对稳定图中数据进行分类，找到图中各分类的聚类中心，并找到与聚类中心最近的数据点，这些数据点所对应的频率及振型即为识别模态参数。

式中，f为计算频率，n为模型的阶数，MAC为模态保证准则(Modal Assurance Criterion):

式中，Φ为模态振型，MAC值在0和1之间，表示模态振型的相关性。当MAC值等于1时，表示模态向量之间是分不开的，即表示相邻不同系统阶数所识别的模态振型一致。当采集MAC等于0，表示模态向量之间是相互正交的，在参数识别中即表示相邻不同系统阶数所识别的模态振型完全不同。

4 算例

4.1 简支梁

为验证随机子空间法、模糊聚类算法在桥梁结构模态参数识别中的可行性与适用性，采用一等截面简支梁作为算例，有限元模型如图2所示。梁全长L=40.0 m，截面面积A=8.215 6 m2，截面高H=2.6 m，截面惯性矩Iz=7.673 6 m4，材料密度 ρ=2 500 kg/m3，弹性模量E=30 GPa。结构被均匀划分为10个单元，11个节点，在11个节点处布置应变传感器。

为避免在模态节点处激励导致无法识别相应的模态参数，在节点3和节点11均加入时长为3.071 s的白噪声激励来模拟现场环境激励(如图2立面图中黑色箭头所示)。选取采样频率1 000 Hz，11个节点共可提出3 071×11=33 781个应变值。由于在实际工程中存在各种噪声干扰，因此采用式S=S(1±λsrand(0，1)，对测量得到的应变值加入噪声，式中S为测量应变值，rand(0，1)是均值为零，方差为1的高斯分布随机数，λs为测量信号的噪声水平。在该简支梁中考虑分别加入λs=1%、λs=5%和λs=10%三种噪声情况。

图2 简支梁有限元模型Fig.2 Finite element model of the simple beam

将考虑了噪干扰的应变时程值作为输入数据，系统阶数取为n=20，22，…，150，对n的每个取值进行一次识别，运行协方差驱动随机子空间法的MATLAB程序，提取(150-20)/2+1=66组频率及振型数据，再将这些数据作为模糊聚类算法FCM程序的输入数据，以频率为横坐标，MAC的第5列值(即简支梁第5节点)为纵坐标绘制FCM稳定图。噪声水平分别为λs=1%、λs=5%和λs=10%的稳定图如图3所示。

图3中所示的稳定图将频率与MAC数据点均分为10类。图中下方曲线为频率谱密度(PSD)曲线，圆圈表示输入数据点，五角星表示每一个聚类的中心，十字表示每一类中距离聚类中心最近的数据点，10个最近数据点所对应的频率及振型即为识别的模态参数。

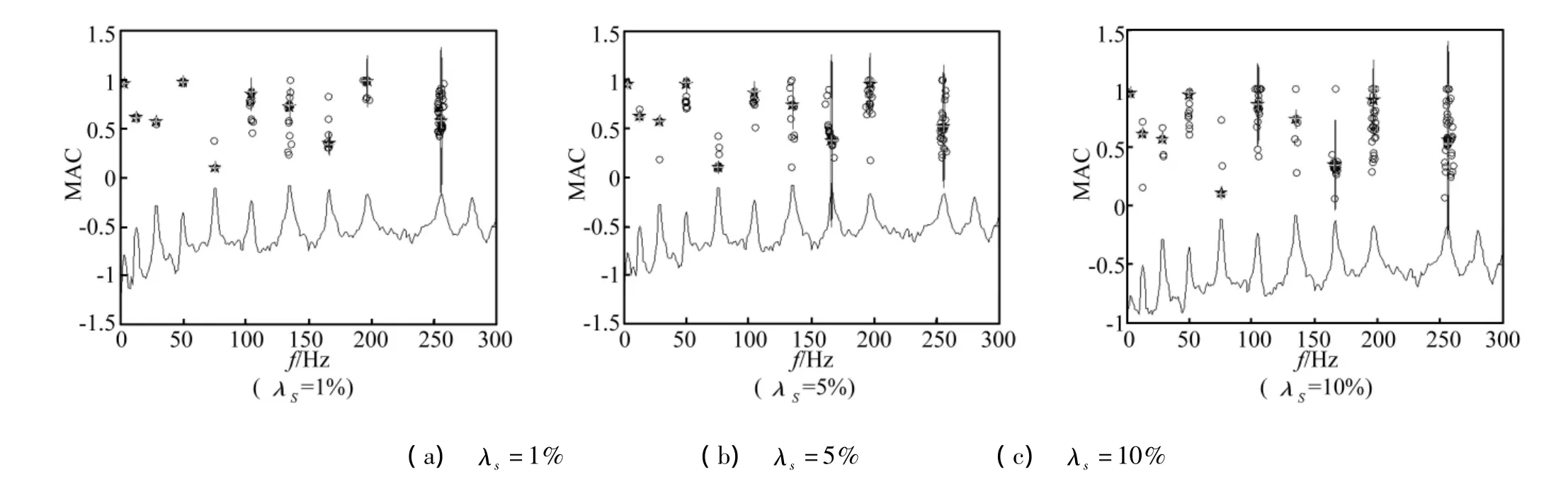
图3 简支梁不同噪声水平下的模糊聚类稳定图Fig.3 Stabilization diagram with different noise levels of the simple beam

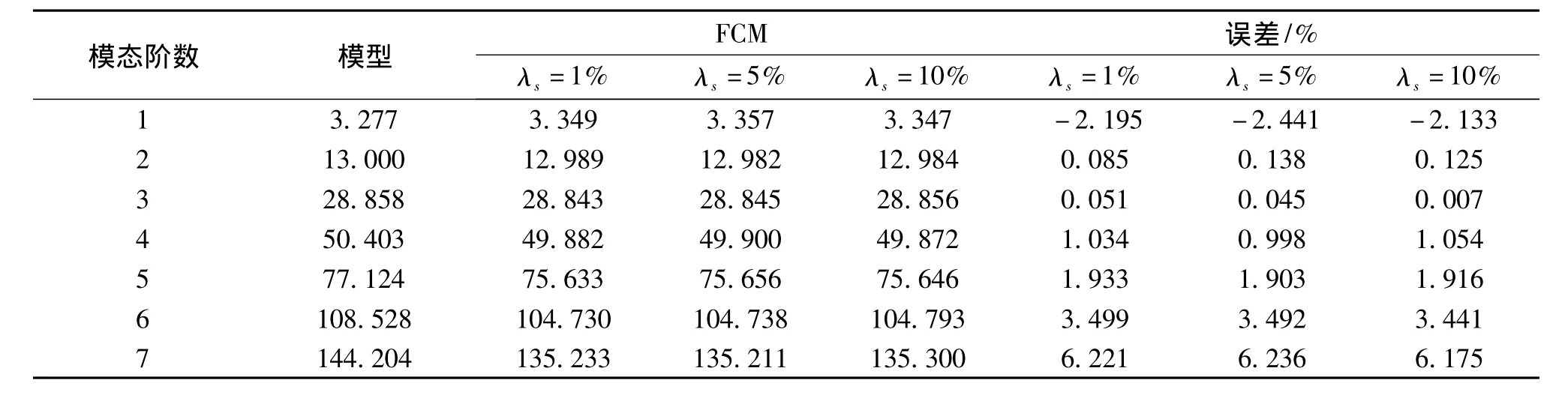
表1 简支梁频率统计结果Tab.1 Frequency statistics of the simple beam

但是，图3所示稳定图中识别的10阶模态并不一定均为真模态，故需剔除其中的虚假模态。本文提出比较圆法，即计算每一聚类所有数据点与聚类中心距离的平均值，并以此平均值为半径，以聚类中心为圆心作圆，通过比较每一个聚类所绘圆的大小即可剔除虚假模态:圆越大(半径越大)也就表征该聚类分散，所对应的模态参数结果越不准确，更易识别到虚假模态。但由于图3横纵坐标比例不同，图中的圆看起来是偏椭圆或一条竖线，图4给出了λs=1%时第1个聚类横纵坐标采用相同比例的放大图，从图中可清晰地看到聚类中心、距中心最近数据点以及聚类圆的大小。

通过比较图3中各聚类圆的大小可知，识别到的前7阶模态相对后3阶模态可靠度更高，可判定为真。表1列出了稳定图中与各聚类中心最近数据点对应的前7阶频率的统计结果。

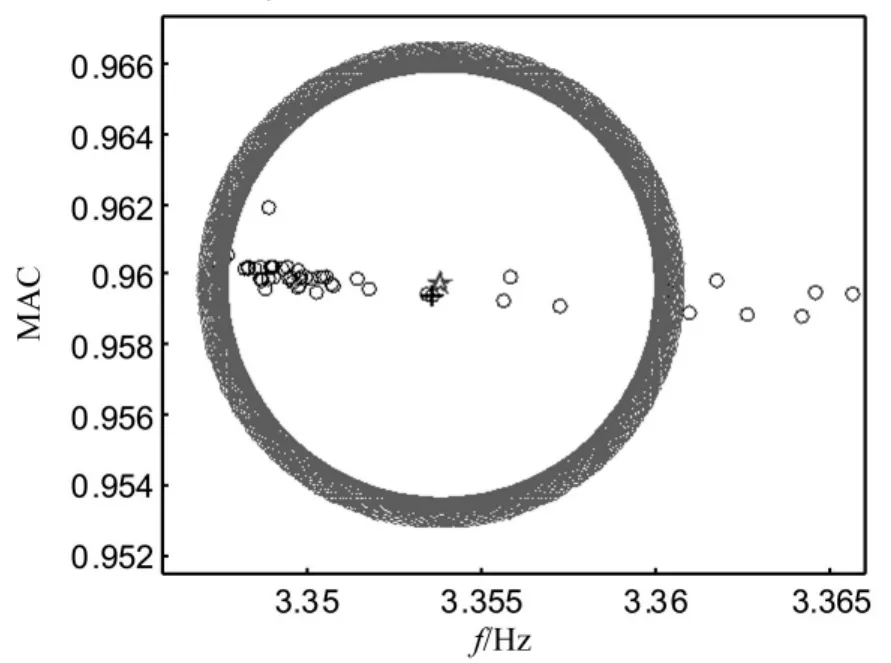
图4 第一个聚类放大图Fig.4 Enlarged drawing of the first clustering

从表1可见:(1)FCM稳定图识别的前7阶频率值与有限元模型相比，计算出的误差最大为6.236%，可见FCM稳定图用于结构参数识别具有较高的准确性。(2)在应变值中加入不同水平的噪声时，模态参数的识别能力并没有随噪声水平的增大而降低，说明基于FCM稳定图的抗噪能力强。(3)不同噪声水平识别的频率与有限元模型结果的计算误差均随模态阶数的增高而增大。

图5给出了噪声水平分别为λs=1%、λs=5%和λs=10%时FCM稳定图所识别的精度较高的前4阶模态参数识别结果，并将有限元模型计算结果绘于图5与稳定图识别结果进行对比分析。

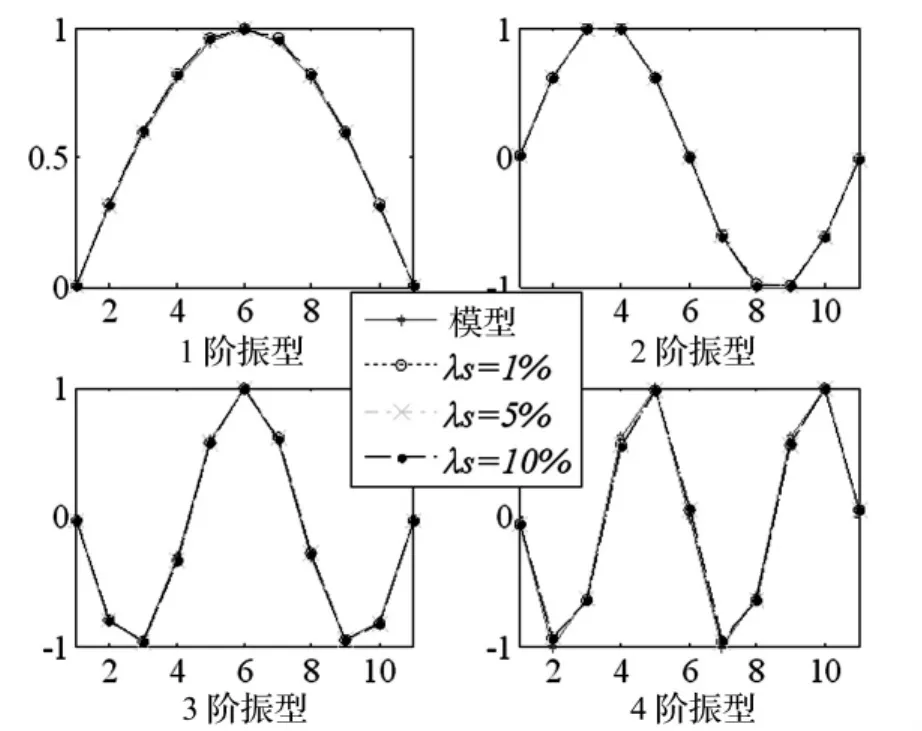
图5 模糊聚类稳定图识别振型Fig.5 Identified mode shapes with FCM stabilization diagram

从图5可知，不同噪声水平识别出的前4阶模态振型结果相近，与有限元结果基本一致。由此可见，在白噪声激励来模拟现场环境激励下，基于模糊聚类算法的稳定图可以非常准确且快速地对结构模态参数进行识别。

4.2 连续梁

为验证实模糊聚类稳定图桥梁结构在复杂的自然激励情况下参数识别中的可靠性，对一座三等跨连续梁结构进行分析。桥梁全长L=60m，截面高H=1.3 m，面积A=0.928 m2，惯性矩I=0.179 m4，材料密度 ρ=2 600 kg/m3，弹性模量E=35 GPa。连续梁有限元模型如图6所示。

图6 连续梁桥有限元模型Fig.6 Finite element model of the continuous beam

图6中，向下的集中力(黑色箭头)对桥梁施加时长为2.401 s的移动瞬时荷载，用来模拟汽车从桥左端移动到右端的自然环境激励。考虑了噪声水平为λs=5%、λs=10%的两种情况。采样频率1 000 Hz，运行协方差驱动的随机子空间法程序，获得n=20，52，…，150共66组识别到的模态参数值(频率及MAC中第15列)，绘制FCM稳定图如图7所示。

从图7可以看出，稳定图中前几阶模态比较圆较大，由此可通过比较各聚类圆的大小来剔除虚假模态。图8给出了有限元模型计算及稳定图识别所得的前5阶竖向应变模态振型结果。前5阶频率的统计结果列于表2。

表2 连续梁频率统计结果Tab.2 Frequency statistics of the continuous beam

由图8可知，在移动荷载激励下，除噪声水平为10%时识别的第1阶振型与有限元结果相差较大外，其余振型结果均与模型结果相近。表2中不同噪声水平稳定图识别的前5阶频率也均与模型结果非常接近，最大误差不超过1%。由此，进一步验证了本文提出的模糊聚类稳定图应用于桥梁结构参数识别的可靠性和有效性。

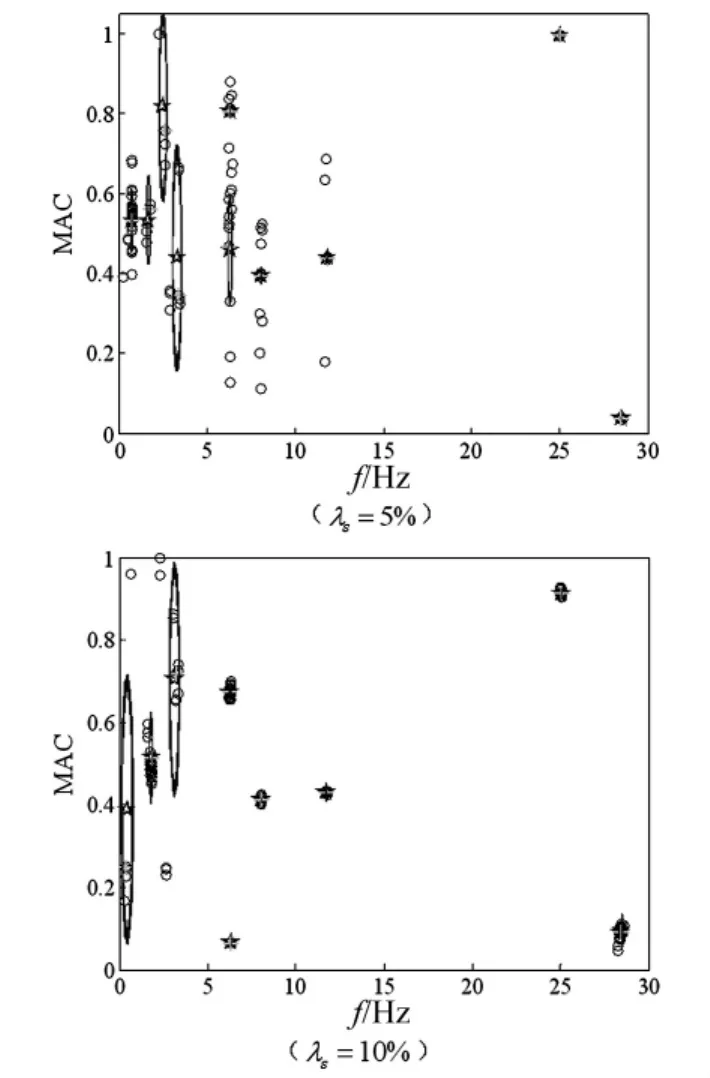
图7 连续梁模糊聚类稳定图Fig.7 Stabilization diagram of the continuous beam

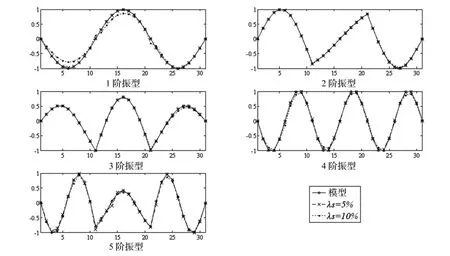
图8 连续梁FCM稳定图识别结果Fig.8 Identified results based on FCM stabilization diagram of the continuous beam

5 结论

将模糊聚类算法应用于稳定图理论，并将该稳定图与协方差驱动的随机子空间法相结合对桥梁结构参数识别进行研究，得到以下结论:

(1)以频率为横坐标，以MAC中的任一列数据为纵坐标的模糊聚类算法稳定图与协方差驱动的随机子空间法相结合可准确识别结构模态参数。

(2)通过比较圆法，使稳定图真假模态的判别不再需要人的主观参与而变得更加智能和准确，使参数识别技术实现自动化。

(3)通过在简支梁和和连续梁的测量信号中加入不同噪声水平后发现，无论是在白噪声激励下还是在移动荷载激励下，FCM稳定图均能准确地识别结构模态参数，说明本文提出方法具有较强的抗干扰性能。

［1］彭细荣，路新瀛，陈肇元.结构应变模态识别的随机子空间方法［J］.振动与冲击，2008，27(6):4-6.

PENG Xi-rong，LU Xin-ying，CHEN Zhao-yuan.Stochastic subspace method for structuralstrain modalparameter identification［J］.Journal of Vibration and Shock，2008，27(6):4-6.

［2］Jansson M，Wahlberg B，A linear regression approach to statespace subspace system identification［J］.Signal Processing，1996，52:103-129.

［3］樊可清，倪一清，高赞明.改进随机子空间系统辨识方法及其在桥梁状态监测中的应用［J］.中国公路学报，2004，17(4):70-73.

FAN Ke-qing， NIYi-qing， GAO Zan-ming. Improved stochastic system identification approach with its application in bridge condition monitoring.China Journal of Highway and Transport，2004，17(4):70-73.

［4］Reynders E，Pintelon R，De Roeck G.Uncertainty bounds on modal parameters obtained from stochastic subspace identification［J］.Mechanical Systems and Signal Processing 2008，22:948-969.

［5］Alicioglu B，Lus H，Asce A M，Ambient vibration analysis with subspace methods and automated mode selection:case studies［J］.Journal of Structural Engineering，2008:1016-1029.

［6］常 军，孙利民，张启伟.基于两阶段稳定图的随机子空间识别结构模态参数［J］.地震工程与工程振动，2008，28(3):47-51.

CHANG Jun，SUN Li-min，ZHANG Qi-wei.Study on the method for stochastic subspace identifying structural modal parameters based on two-stage stabilization diagram［J］.Journal of Earthquake Engineering and Engineering Vibration，2008，28(3):47-51.

［7］Fan J L，Zhang Z Y，Hua H X.Data processing in subspace identification and modal parameter identification of an arch bridge［J］.Mechanical Systems and Signal Processing，2007，21:1674-1689.

［8］ Scionti M，Lanslots J P. Stabilisation diagrams:Pole identification using fuzzy clustering techniques［J］.Advances in Engineering Software，2005，36:768-779.