黄土丘陵半干旱区柠条林株高生长过程新模型

2013-09-07王振凤郭忠升郭满才袁志发

生态学报 2013年7期

赵龙，王振凤，郭忠升，郭满才，袁志发

(1.西北农林科技大学理学院，杨凌 712100;2.西北农林科技大学水土保持研究所，杨凌 712100;3.中国科学院水利部水土保持研究所，杨凌 712100)

柠条(Caragana korshinskii)是锦鸡儿属的一种植物，是我国西北、东北、华北地区营造水土保持和防风固沙林的主要灌木树种［1］。柠条林生长状况关系到半干旱地区的植被恢复和生态环境建设。利用数学模型描述植物生长过程是一种常用方法［2］。通常以“S”型曲线模拟植物生长过程［3-5］，最普遍使用的是1838年由Verhulst提出的Logistic方程。该模型反映了生命体生长过程中的较简单的密度制约关系，然而自然界中生命体生长指标的变化较为复杂，这种简单的变化关系已经不能满足对实验数据处理的要求，许多研究者对该模型实行多种变形［6-11］。但由于生长环境非常复杂，有关植物在极高的密度制约下生长曲线的单调性发生改变的报道较为少见。在黄土丘陵半干旱地区，柠条在1年内的生长并非严格单调增加，其生活史较长。柠条生长不仅有日变化［12-13］，季节变化，而且还有年际变化。本研究通过分析半干旱区柠条生长过程，试图建立柠条林1年和多年生长模型，为多年生植物生长过程模拟、植被恢复［14］和生态环境建设提供参考。

1 研究区概况

研究区位于黄土高原西部的宁夏固原市原州区河川乡固原生态试验站上黄生态实验站。区内地势起伏，沟壑纵横，水土流失严重，地理位置为东经 106°26'—106°30'，北纬 35°59'—36°02'，区内沟沿线以上坡度较缓，沟沿线以下坡度大于 25°。海拔高度约1534—1824m。年均气温7.0°C，1983—2001平均年降雨量415.6mm，降水年变率22.8%。无霜期152d，土壤为黄土母质发育的黄绵土。试验地的草本植物主要有长芒草(Stipa bungeana)、阿尔太狗哇花(Heteropappus altaicus)、茭蒿(Artemisia giraldii)、百里香(Thymus mongolicus)等。

2 试验设计

柠条成林选在黑刺峁东坡中部坡度较缓，海拔约1650m，1986年在黑刺峁建有大面积柠条林，2002年4月对16年生柠条成林进行面上调查，选择立地条件相对均一的缓坡地段为实验样地，并对柠条成林进行疏伐处理，保存密度为 87、71、51、32、16 丛/100m2［1，15-16］。幼林小区设在黑刺峁中下部多年撂荒地上，坡度 8°—10°。将撂荒地分成5个5m×20m=100m2的矩形密度处理小区，密度处理之间间隔1m。5个密度小区播种量分别为2.0、1.5、1.0、0.5kg/100m2和撂荒地对照组。2002年6月24日撒播柠条种子，2002年9月中旬采用样线法调查不同播量小区的柠条幼林密度。柠条成林2002年到2004年的生长指标测定从4月中旬到10月，每个密度处理选取具有平均冠幅的样丛10个，在每个样丛内选择一个平均基径和最大基径的枝条作为样枝，选择一个平均高和平均基径的枝条作为样枝，样本共40株。对样枝和基径观测部位进行标记。每年在生长季节每隔15d测定一次单枝基径、株高。基径用游标卡尺测定，株高用卷尺测定。40株样本中30株作为建模数据，10株作为检验数据。

3 结果与分析

3.1 Logistic模型

Logistic模型解析表达式为:

式中，t为时间，y为植株株高(y＞0)，k，a，b为方程的参数，其中k表示一定时期内的生长上限(k＞0)，b表示内禀生长率(b＞0)，a表示与曲线位置有关的参数。

以密度为87丛/100m2的柠条成林作为研究对象，上黄地区柠条枝条叶芽的萌动时间为4月中旬，以2002年4月15日作为生长起始时间，为避免时间轴过长，设以后每隔1天增加0.1。按照上述做法累计，2002 年存在观测记录的时间点为:2.8、4.3、6.2、7.7、9.2、10.8、12.3、14、15.4、17。将 2002 年和 2003 年的休眠期也按照每隔1天增加0.1继续累计，可得2003年、2004年数值观测点分别为:2003年39.7、41.2、42.8、44.4、45.9、47.9、48.9、50.8、53.7;2004 年 73.3、76.3、79.4、82.4、85.6、88.6。

用Levenberg-Marquardt法分别对2002年、2003年、2004年的观测值进行拟合，其结果如下:

2002—2004年3a的函数图象见图1。

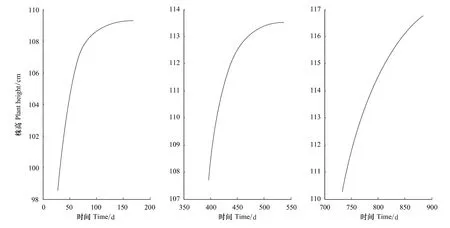
图1 2002年、2003年、2004年生长曲线图Fig.1 The growth curve of caragana in 2002，2003，2004

3.2 改进模型

对模型(1)求导数得Logistic方程的微分形式为:

以2002年生长拟合结果为例画出(4)式的图像见图2。

经典Logistic模型的机理为:生长速率与生长空间k-y成正比，与当前生长量y成反比;相对生长速率仅与k-y成正比。经典Logistic模型仅以当前生长量为限制因子，与时间无关，称为自治的。k-y可看作是密度对于生命体生长的线性制约，通常情况下引入新的参数将Logistic模型变形，使得线性制约部分成为非线性的［7-8，11］。由于植物生长是一个复杂过程，受多个因素影响，是多种机理共同作用的结果［2］。植物体本身存在着新陈代谢过程，在生长期进行光合作用和呼吸作用。新陈代谢对植物生长的影响随时间而变化。

图2 2002年相对生长速率随时间的变化关系Fig.2 The relationship between relative growth rate and time in 2002

观察该密度下的柠条林生长，发现到8月或9月时，受气候和土壤干旱的影响，林地出现大面积落叶现象，到10月时，叶子全部落完，此时生长期结束。进入落叶期时，光合速率下降，呼吸速率也下降，光合速率小于呼吸速率，枝条含水量下降和干旱导致植物体萎缩，株高随时间小幅度减少。可见柠条生长随季节变化过程中，一直存在着环境阻力，并且落叶时的阻力对柠条生长影响显著，使该时期生长速率和相对生长速率均表现为负值。

考虑到上述过程，将Logistic模型相对生长速率表达式(4)改为:

式中，参数K，a为常数，b为内禀生长率(b＞0)，c表示生长阻力因子(c＞0)。K，a均表示与曲线位置有关的参数。

方程(7)在生长区间内为连续函数，存在极值点，令导数为零得:

改进模型的相对生长率等于生长部分的相对生长速率与阻力部分的相对变化率之和。当生长动力大于阻力时，植物表现为生长，株高生长增加;当生长动力小于生长阻力时，阻碍生长，株高生长减少。生长末期的密度制约强度对株高生长的影响显著，使得生长曲线的单调性发生改变。

极值纵坐标为年生长最大点，记为生长顶点;是改进模型函数在定义域内最大值。超过最大值之后株高生长开始减少，直至生长期结束。将生长顶点与生长期结束时植株高度之差称为生长过程中的生长损失。

由于改进模型的微分表达式使用了相对生长速率与时间的关系式，故新模型中K与原始Logistic模型的参数k不同，改进模型中参数K是根据积分常数得到，与曲线在坐标系内的相对位置有关。Logistic模型参数k仅表示上渐进值，而改进模型中K，a，b，c共同决定了生长顶点。在对不同年柠条林生长的拟合过程中，所得到的参数a与b的比值决定了生长曲线在横坐标轴上的相对位置。

以2002年和2003年的观测值为例，用Levenberg-Marquardt法进行拟合［17-18］，时间的取值同上节，得到以下结果:

画出此函数的图像和相对生长速率与时间的关系见图3。

图3 2002年高生长和相对生长速率随时间的变化Fig.3 The change of height and relative growth rate with time in 2002

拟合结果代入(9)式得t=12.124485，对应的真实时间为8月13日，在此之后方程(7)中株高的阻力因子具有显著作用，阻碍生长。将t=12.124485代入新模型，得生长顶点为109.638069cm，又将t=17代入新模型，得最终株高值为108.237665cm，生长损失为1.400403cm。

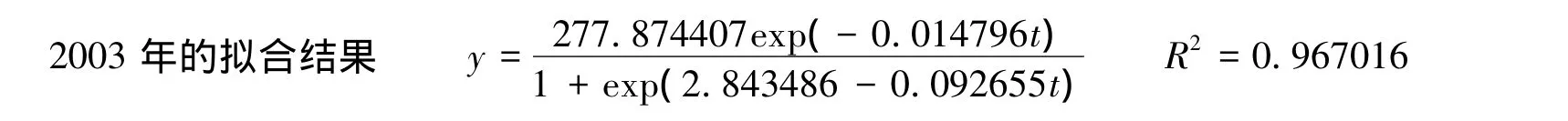
画出此函数的图像和相对生长速率与时间的关系见图4。

拟合结果代入(9)式得t=48.610664，对应的真实时间为8月14日，在此之后方程(7)中株高的阻力因子具有显著作用，阻碍生长。将t=48.610664代入新模型，得生长顶点为113.742512cm，又将t=17代入新模型，得最终株高值为112.230081cm，生长损失为1.512430cm。

从Logistic模型的模拟结果中可看出，上渐进值k随着年度逐渐增加，而在改进模型中参数K也随着柠条生长逐年增加。

从模型函数(7)中生长部分的分母中存在如下等式:

比较不同生长年中a除以b的值可得出模型函数(7)在横轴上相对位置的变化情况，不同生长年中参数a与b的比值见表1。

同一个模型不同年的a与b的比值均逐渐增大，这与上节中坐标轴的设定是相符合的，由于2002年的生长起始时间是从零开始计算，故2002年的模拟结果中参数a很有可能出现负值的情形。按照上节中数值时间点的累计方法，当a与b的比值增大时，生长曲线沿平行于横轴的方向向右移动，故2003年和2004年的比值一定大于零。

图4 2003年生长方程及相对生长速率随时间的变化关系Fig.4 The change of height and relative growth rate with time in 2003

表1 在不同年内两种模型的参数a与b的比值Table1 In different years，the ratio of parameters a and b for two models

用检验数据对两个模型的模拟值分别进行检验，求出2002年和2003年模拟值与观测值之间的相关系数(表2)。

表2 两年中两个模型模拟值与观测值的相关系数Table2 Correlation coefficient of observed value and simulated value for two models in two years

从表2中可看出2002年和2003年Logistic模型的相关系数较高，而改进模型的相关系数均大于Logistic模型的相关系数。表明引入生长阻力因子c后，可以更好地反映1年内株高的变化规律。

两年中改进模型拟合结果的残差分析图［19-20］见图5，图6。

对比图3和图4可看出，2002年和2003年柠条成林生长情况存在一定程度的差异，这是由于试验地处于半干旱区，土壤储水量长期不足，降水量对柠条生长影响显著。2002年和2003年的降雨量如图7所示，这两个生长年中2002年6月的降水量为全年最大，2003年8月的降水量为全年最大。2002年6月的降水充足，而且该时间的柠条全部展叶，高生长处于全年生长较快的速生期;降水促进了柠条生长，该年度降水在当年就被柠条林充分利用。而在2003年生长初期土壤含水量较低，6月降水明显不足，在大量需要水分的速生期，该地区柠条林未能得到有效降水，柠条生长受到影响。虽然2003年为丰水年，但是8月时的降水才达到全年最大，此时柠条生长处于生长后期，8月长势小于6月长势。考察柠条成林的年生长过程，发现8月中旬时该密度处理小区柠条林落叶最严重，枝条与叶片含水率下降，部分叶片变黄［1］，2003年8月的最大降水未得到充分利用;从极值点的计算结果中得出，两个极值点对应的真实时间均位于8月中旬。

图5 2002年改进模型的残差分析图Fig.5 The residual analysis diagram of improved model in 2002

图6 2003年改进模型的残差分析图Fig.6 The residual analysis diagram of improved model in 2003

从上述分析能够得出2002年柠条林对降水量的利用程度大于2003年的，2003年的充足降水在当年未得到有效利用，降水储存在土层中供给下一年的柠条林生长。所以2003年柠条林生长的阻力较2002年大，从拟合结果中可看出生长的阻力因子c2003＞c2002成立;因降雨的限制作用，2003年柠条林生长的动力较2002年小，从拟合结果中可看出内禀生长率参数b2003＜b2002成立。因此不同年内的柠条成林生长呈现各自的特点，从生长方程上看2002年生长量大于2003年的;从相对生长率的图像上看，2002年变化幅度也大于2003年的;与实际的生长过程符合。

3.3 连年生长模型

上节的研究结果表明上黄生态站的柠条林生长在一年内的变化不具有严格单调性，在生长季末期株高小幅度变小，但柠条为多年生灌木树种，仅1a观测结果不能充分说明该地区柠条林的生长情况，有必要探讨林地的年际变化。

在2002年的模型中最后一个观测点为10月初的观测值，也即将t=17代入模型(7)，2002年拟合结果为y=108.237665;2003年模型中最初一个观测点为5月中旬的观测值，将t=39.7代入模型(7)，2003年拟合结果为y=107.701089;2003年模型中最后一个观测点为10月初观测值，将t=53.7代入模型(7)，2003年拟合结果为y=112.230081;利用第3节的2004年的拟合结果得出最初观测点为t=73.3时，y=110.243308。

对比这3a生长段的两个间隔区:株高在第1年生长期末的函数值总大于第2年初的函数值，表明该地区柠条林生长的年际变化也不具有严格单调性，连年生长过程中也存在随时间递减情形。具体考察柠条林在休眠期的变化情况发现，进入10月初后，试验地地处宁南山区，天气转冷，气候干燥。试验地2002年和2003年全年的月平均温度变化情况如图8、图9(以2002年1月记为1，每隔1个月增加1)。从图中看出这2a的12月和1月的平均温度在－5℃左右，气温较低，柠条容易受冻害［12-13］，日最低温度可达－15℃。冬季的温度较低，气候干燥，顶芽在冬季极易失水而干缩导致柠条顶枝上部的一小段枝条及芽越冬后死亡，这种现象称为干梢现象。

图8 2002年1月至2002年12月平均温度变化情况Fig.8 Changes in monthly mean temperature during JAN 2002 to DEC 2002

图9 2003年1月至2003年12月平均温度变化情况Fig.9 Changes in monthly mean temperature during JAN 2003 to DEC 2003

干梢现象导致第2年活芽出现高度普遍低于上年生长期末活芽出现高度，这使得年际变化曲线的冬季部分也存在着一段时间的逐渐减小。柠条多年生长是一个连续过程，无论是生长过程、落叶过程还是干梢过程，这些过程均缓慢进行，所以年际变化曲线应具有连续性，至少是分段连续的。从总体来看，第2年株高要大于第1年株高，也就是说，柠条林在冬季经历的干梢过程有一个限度，当柠条经历了非常寒冷、干旱的冬季时期后，干梢过程会停止。所以研究相邻年生长曲线的光滑连接和干梢的终止点是有意义的。

为此提出2002年和2003年两个生长年的分段函数［21］如下:

y1(t)，y3(t)为上节中所得的拟合结果，由于植物体生长的连续性，故该分段函数在节点处也应满足连续性并且是光滑的，y2(t)应满足如下条件:

设y2(t)为三次多项式函数，解析式为y2(t)=at3+bt2+ct+d，将y2(t)代入条件(11)可得:

按照求解代数余子式的算法对上述矩阵求逆，结果如下:

最终得到y2(t)的解析式为:

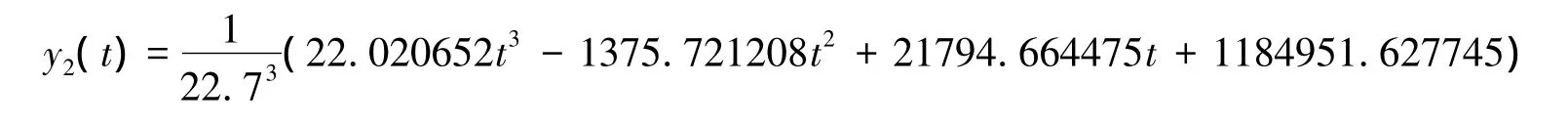
同理，若以2003年和2004年的柠条生长作为研究对象也可建立分段模型如下:

其中y5(t)为第三节的结果，y4(t)的解析式如下:

综合(10)、(12)两式得出3a的生长方程为:

画出该函数图像如图10所示，连年生长模型中共有极值点4个，从小到大排列依次为t1，t2，t3，t4其中t1，t3已经在上节中求出，t2，t4应分别从y2(t)，y4(t)中求出。

由 yi(t)=at3+bt2+ct+d，i=2，4

得y'i(t)=3at2+2bt+c

令y'i=0，解一元二次方程可得t2，t4。

令 y'2=0，经求解得两根为31.010788、10.638636，由 t2的取值范围知 t2=31.010788。

令 y'4=0，经求解得两根为66.258120、43.259543，由 t4的取值范围知 t4=66.258120。

t2，t4可看作干梢的终止点，由t2，t4的数值推算其所对应的真实时间分别为:2003年2月18日和2004年2月6日。柠条在生长期结束之后，进入冬季休眠期，受干旱和寒冷的影响［12-13］，再加上该地区冬季的风力较大，出现了干梢现象，使得新生枝条上部一小段死亡，因干梢所引起的株高减少量在冬季随时间缓慢增加，当达到t2，t4所对应的时间时，干梢过程基本结束，进入下一年生长。

4 讨论

经典生长方程有 Logistic，Gompertz，Bertalanffy，Mitscherlich，Richard，Weibull等模型［3，5］，建立方程时均以严格的单调增加为基础;经典生长方程中密度对生长的制约强度始终小于生长动力。因Logistic模型应用广泛，在研究生命体生长时考虑用引入新参数或添加生长机理等方法在该模型基础上变形［6，11-12］。上述变形也没有改变模型函数在定义域上的单调性。应用生长方程来描述植物生长过程时，大多以乔木为研究对象;以灌木为研究对象的报道较为少见。相比于乔木林，灌木林在生长时期密度对生长指标的干预更加明显，在生长期内，受环境(低温和干旱)的影响，有可能生长指标随时间减小。

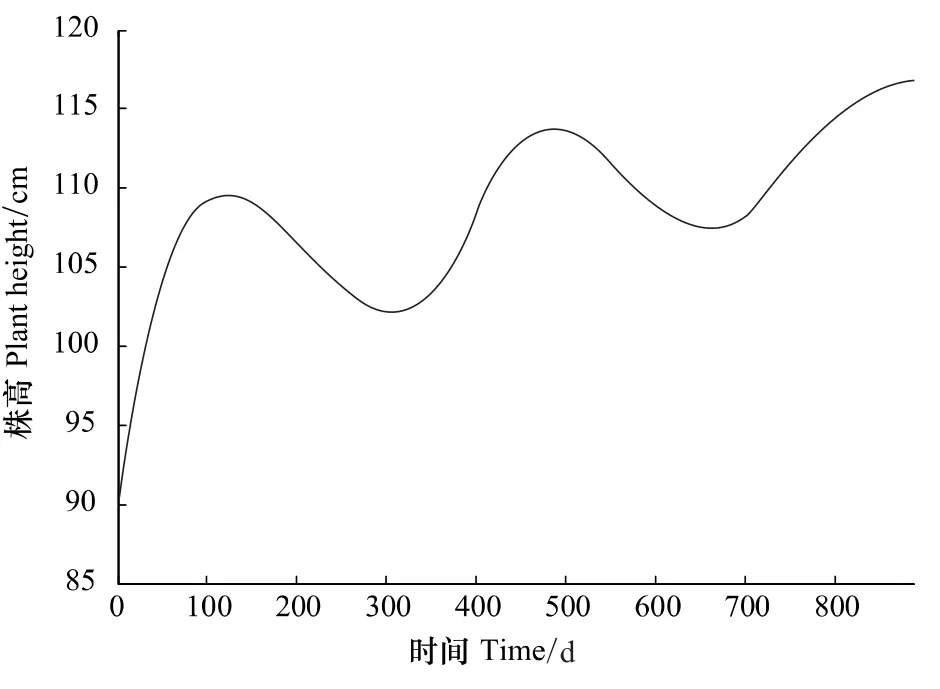
图10 2002年到2004年的连年生长模型Fig.10 The growth curve for caragana in 2002 to 2004

柠条的生长环境复杂多变，特别在黄土丘陵半干旱地区，柠条林的生长过程表现出一定的复杂性。柠条在生长期受气候变化和新陈代谢的影响，使得株高生长在生长期末不再随着时间的推移而单调增加;在休眠期受环境阻力的影响，而且在该时期出现干梢现象，降低株高生长，休眠期的干梢现象在以往的研究中较少体现。

本研究将生长阻力考虑到模型内，假定生长过程中阻力的作用是一个常数，令相对生长速率出现负值，并积分得到了新的生长模型。不同生长年中参数模拟值不同，参数的变化趋势与年生长的特殊规律紧密联系。改进模型中的参数K较原Logistic模型发生了变化;本文所涉及两个模型的参数a解释为位置参数，与对人口数量变化，害虫密度变化规律的研究方法不同，他们将a看做与初始密度和最大容纳量有关的参数［23］，故种群生态学中Logistic的参数不都是独立的［24］。而本文中进行曲线拟合时，模型参数均看作是相互独立的，且a与b的比值呈现出一定的变化规律。本文所建立的改进模型只针对密度为87丛/100m2柠条成林，而疏伐处理后确定的密度梯度较大，在年生长末期(8月到9月)，低密度处理林地生长情况与高密度的不同，落叶程度较轻，部分枝条未落叶;所以在生长末期低密度柠条林的光合速率不一定小于呼吸速率，其密度制约强度小于高密度的，在低密度条件下新模型是否适用有待进一步确定，因此改进模型存在密度适用范围。从图3、图4可以看出，受降雨影响2002年总生长量明显高于2003年的。由于柠条为多年生灌木，在黄土丘陵半干旱地区，柠条的生长不仅具有季节变化，而且还有年际变化，因此在模拟柠条生长过程时，不仅要考虑柠条的季节变化，而且还要考虑年际变化。

本文通过对多年生柠条生长资料的分析，推导了一种模拟柠条生长的Logistic模型的改进模型和连年生长模型。新模型可用来分析柠条幼林的生长情况，例如新生林中生长拐点、速生区间的确定等［25］;Logistic曲线是关于拐点对称的，而改进模型的拐点距离生长起始点较近，所以新模型与年生长的实际过程更为接近。从目前的分析结果来看，该模型能较好地拟合半干旱地区柠条生长过程;其是否适合于柠条生活史或半干旱地区其他多年生植物生长过程，有待进一步研究。

［1］ Guo Z S.Vegetation Carrying Capacity of Soil Water in A Semi-arid Loess Region of Loess hilly in the Loess Plateau，［D］.Yangling:Northwest A＆F University，2004.

［2］ Lu E S，Guo M C，Song S D，Yuan Z F.A kind of non-autonomous Logistic growth curve and its application Journal of Northwest Science and Technology University of Agriculture and Forest(Natural Science Edition)，2002，30(4):127-129.

［3］ Liu P，Ma L Y，Jia L M.Study on individual tree height growth model for Pinus tabulaeformis plantation.Forest resource management，2008，(5):50-56

［4］ Xing L F，Sun M G，Wang Y J.Richards growth model of living-organism.Journal of biomathematics，1998，13(3):348-353.

［5］ Duan A G，Zhang A G，Tong SZ.Application of Six Growth Equations on Stands Diameter Structure of Chinese Fir Plantations.Forest Research，2003，16(4):423-429.

［6］ Zhang D Y，Zhao SL.Study on the model of forest population density change during self-thinning.Scientia silvae sinicae，1985，21(4):369-374

［7］ Li X Y，Zhao SL，You Z L.A self-adaptive model of population growth and its parameter estimation，Acta Ecologica Sinica，1997，17(3):311-316

［8］ Liu JF，Hong W，Li J H，Zheng Y M.Population ecology of Castanopsis kawakamii.Growth dynamics of dominance of Castanopsis kawakamii population.Chinese journal of applied ecology，1998，9(5):453-457

［9］ Seiichi Sakanoue.Extended logistic model for growth of single-species populations.Ecological Modelling，2007，205:159-168

［10］ John H M，John J.An open-ended logistic-based growth function:Analytical solutions and power-law logistic model.Ecological Modeling，2007，204:531-534

［11］ Yu A H.A study on Logistic Model.［D］，Nanjing，Nanjing Forestry University，2003

［12］ Li Y Y，Shi H，Zhang A B，Tan H C.Daily Changes in Radial Growth of Several Tree Stems and Their Response to Environmental Factors in Loess Hilly Region.Journal of Soil and Water Conservation，2007，21(6):170-173.

［13］ Zweifel R，Häsler R.Frost-induced reversible shrinkage of bark of mature subalpine conifers.Agricultural and Forest Meteorology，2000，(102):213-222.

［14］ Jiang F Q，Lu F Y.The model of estimating above-ground biomass of Caragana Microphylla brush.Acta Ecologica Sinica，1982，2(2):103-110

［15］ Guo Z S，Shao M A.Use of the Theory of Soil Water Carrying Capacity for Vegetation in Practice.Journal of Natural Resource，2009，24(12):2187-2193.

［16］ Guo Z S，Shao M A.Preliminary Study of Vegetation Carrying Capacity of Soil Water(VCCSW).Science and Technology Review，2006，24(2):56-59.

［17］ Zhou JY，Song S D，Yuan Z F，Hu Y.Fitting curve for compartmental analysis by Marquardt's Algorithm.Journal of Northwest Science and technology University of Agriculture and Forest，1996，24(1):75-78.

［18］ Wang M M，Li D M.Fitting logistic curve by Marquardt's Algorithm.Acta Ecologica Sinica，1986，6(2):142-147.

［19］ K.Rennolls.Forest height growth modeling.Forest Ecology and Management，1995(71):217-225

［20］ Liu P，Wang Y T，Ma L Y.Dynamic prediction and verification of individual tree DBH growth process of pinus tabulaeformis plantation.Journal of Northwest Forestry University 2010，25(4):139-143.

［21］ Yuan Z F，Xie K R.Several kinds of methods of fitness of multiple growth curve.Acta Northwest Agriculture University，1986，14(2):62-69.

［22］ Zhou Y X，Song SD，Fan JF.The analysis of high growing curve in seedling period of Paulownia.Shanxi Forest Science and Technology，1996，11(3):1-4.

［23］ Deng M M，Gao H H，Li D，Hu X S，Hu Z Q，Zhao H Y.Effects of temperature on body color in Sitobion avenae.Acta Ecologica Sinica，2011，31(23):7203-7210.

［24］ Yuan Z F，Zhou JY.Multivariate Statistical Analysis1sted.Beijing:Science Press，2003:142-147.

［25］ Zhang L X，Liu X Z.The analysis and application of the two important characteristic points on Logistic curve.Journal of Heibei Forestry College.1992，7(2):154-158.

参考文献:

［1］郭忠升.黄土丘陵半干旱区土壤水分植被承载力研究，［D］.杨凌:西北农林科技大学，2004

［2］卢恩双，郭满才.宋世德.袁志发.一类非自治的Logistic生长曲线及其应用.西北农林科技大学学报(自然科学版)，2002，30(4):127-129

［3］刘平，马履一，贾黎明.油松人工林单木树高生长模型研究，林业资源管理，2008，(5):50-56

［4］邢黎峰，孙明高，王元军.生物生长的Richard模型.生物数学学报，1998，13(3):348-353

［5］段爱国，张建国，童书振.6种生长方程在杉木人工林林分直径结构上的应用.林业科学究，2003，169(4):423-429

［6］张大勇，赵松岭.森林自疏过程中密度变化规律的研究.林业科学，1985，21(4):369-374

［7］李新运，赵善伦，尤作亮.一种自适应的种群增长模型及参数估计.生态学报，1997，17(3):311-316

［8］刘金福，洪伟，李家和，郑燕明.格氏栲种群生态学研究3格氏栲种群优势度增长动态规律研究.应用生态学报，1998，9(5):453-457

［11］余爱华.Logistic模型的研究.［D］，南京:南京林业大学，2003

［12］李秧秧，石辉，张安邦，谭红朝.黄土丘陵区几种林木茎干径向生长的日变化及其对环境因素的响应.水土保持学报，2007，21(6):170-173

［14］姜凤岐，卢凤勇.小叶锦鸡儿灌丛地上生物量的预测模式.生态学报，1982，2(2):103-110