银行同业拆借利率动态相关性研究——基于多元GARCH模型的分析

杨 红，董耀武

(1.四川外语学院应用外语学院，重庆 400031;2.重庆市合川区委党校，重庆 401520)

商业银行同业拆借市场是一个充满不确定性的要素市场，也是金融机构间融通资金的主要途径。同业拆借市场利率因其特有的市场敏感性，能在一定程度上反映社会宏观经济运行及金融市场资金供求关系，这使其在整个金融利率结构中具有一定的主导作用。因此，研究银行同业拆借市场利率期限结构变化规律，将有利于中国人民银行在经济波动时有效地调整货币政策，也有利于金融机构更好地把握资本供求做好金融实务，这对于我国金融市场加强金融风险管控、推动金融改革以实现市场有序发展具有重要意义。

一、研究文献回顾

对利率期限结构的研究主要是从模型化开始的，最初构建了单因子扩散模型。比如Merton(1973)［1］构建的模型指出短期利率服从随机方程，但利率均值回复与现实不符。为此，Vasicek(1977)［2］提出的单因素模型能很好地拟合实际。谢赤和吴雄伟(2002)［3］、林海和郑振龙(2005)［4］、严玉敏(2009)［5］等实证也认为 Vasicek 模型拟合优度高。进一步地，CKLS［6］模型认为描述短期利率动态过程时要充分考虑水平效应。但Brenner、Harjesm和Kroner(1996)［7］指出CKLS模型忽视了波动聚类效应，为此构建了GARCH过程以分析外部冲击对利率动态模型的影响。此外，Longstaff和Schwartz(1992)［8］特别指出利率期限结构模型存在着条件异方差。

在对时间序列的动态相关性特征研究中，Bollerslve、Engle和Wooldridge(1988)［9］用对角矩阵来减少VECH模型中的待估参数。BEKK模型［10］虽减少了待估参数且保证了协方差的非负性，但该模型随变量的增加，推定参数也相继增加。随后，Bollerslve(1990)［11］的CCC-MVGARCH模型也具有BEKK模型特点，但缺陷是模型严格的前提假设致使其实用性降低。基于以上研究，Engle和Sherpard(2001，2002)［12］构建了 DCC-MVGARCH模型。在 GARCH模型功能上，洪永淼和林海(2006)［13］指出GARCH模型能在很大程度上提高短期利率动态模型的拟合效果。

综上所述，国内外对金融市场利率(期限结构)及其模型化做了很多研究，但对于同业拆借市场利率(期限结构)及其波动过程的动态研究还比较少。因此，本文基于Vasicek模型，引入相关GARCH模型对所选银行间同业拆借利率数据序列进行动态相关性等特征分析，以考察我国银行同业拆借市场的有效性。

二、理论框架及数据说明

(一)Vasicek模型及其离散化

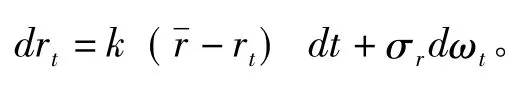
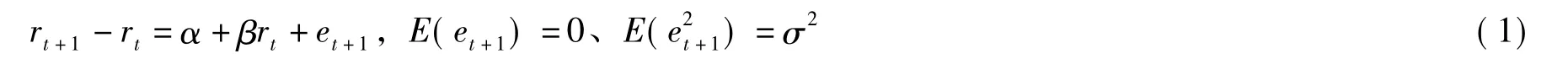
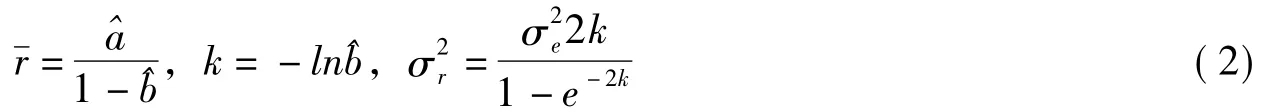
(二)多元GARCH模型

1.VECH模型

结合Vasicek模型，Bollerslve、Engle和Wooldridge(1988)［11］提出VECH模型，主要结构为:

2.对角BEKK模型

为减少GARCH模型参数量，保证矩阵Ht正定性，Engle和Kroner(1995)［12］基于VECH模型提出BEKK模型。具体形式为:

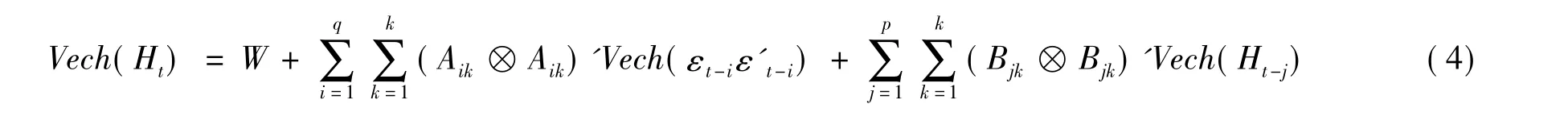
3.不变条件相关GARCH(CCC-MVGARCH)模型

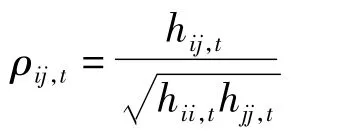
其中，Ht矩阵的第(i，j)个元素就是hij，t(表示在 t-1时刻，Yi和 Yj的条件协方差)。假定 ρij，t为常数ρij，则Ht可写作:

Dt所有条件方差GARCH形式如式(5)所示:

随机变量yi和yj常相关系数可表示为(6)式:

4.动态条件相关多元GARCH(DCC-MVGARCH)模型

DCC-MVGARCH模型是由以上模型发展而来的，其动态结构可设定为:

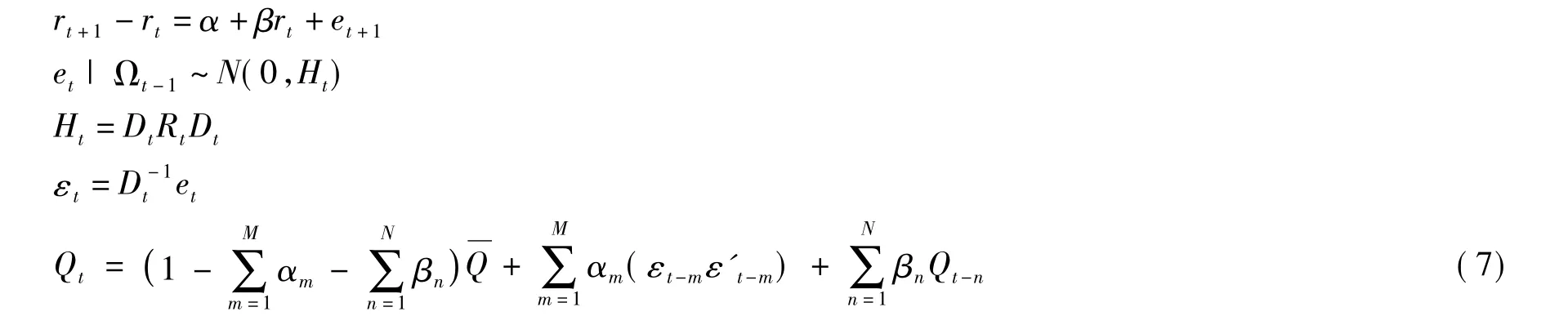
对数据进行序列相关性检验和异方差性检验之后，在(7)式正态性假设条件下，可对DCC模型进行极大似然估计，对数似然函数如下:

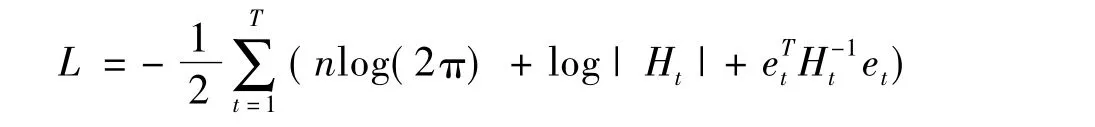
经整理得:

(二)数据说明

1.数据来源

论文选取我国银行间同业拆借市场1998年1月至2011年12月数据。以1998年为始，是因为这时候我国银行间同业拆借市场初步形成，自1998年以来，利率生成受政府政策扰动相对较少。又因银行间同业拆借市场14天(d)和120天(d)两组数据部分数据缺失，因此本文选用1天(d)、7天(d)、30天(d)和90天(d)四组加权平均月度利率数据为研究对象。数据来源为wind资讯。

2.数据单位根检验

理论上认为，如果利率时间序列是平稳的，则说明利率序列有均值回复现象，就可用利率时间序列进行实证模拟。表1为用ADF方法给出的4个序列的检验结果，其中第一列括号内容为该期限序列的数据均值。如表1所示，对于利率序列，1d、7d、30d数据序列在1%的置信水平下拒绝存在单位根，只有90d数据序列存在单位根，而在5%的水平下四组序列数据都拒绝存在单位根;对于利率差分序列，所有期限利率数据序列均不存在单位根。这说明论文选取的利率数据序列是平稳的，因此具有均值回复现象。

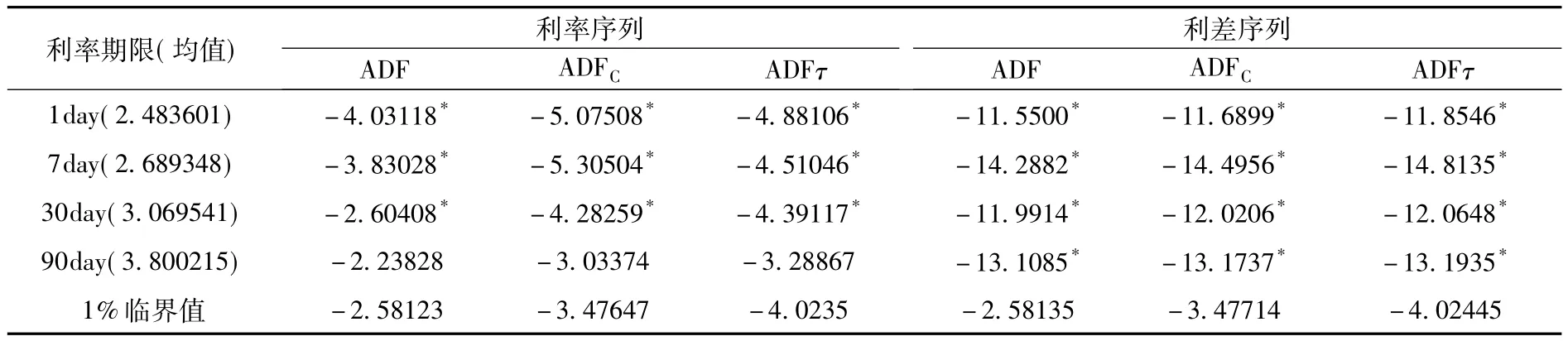
表1 银行间同业拆借利率单位根检验

三、实证分析

(一)均值方程估计结果及分析

均值方程(1)式估计结果如表2所示。其中BEKK和VECH方法估计值结果一致，表中所示三种方法估计值具有很高的置信水平，均值回复显著，表现出较好的估计效果。从表2还可看出，除90d序列数据以外，其余期限利率表现出随利率的到期日期时间变长，均值回复速度在加快。90d数据序列的异常表现，可能是因为利率期限的变长，促使外部冲击对利率的影响变得显著。

表2 多元GARCH均值方程估计值

表3 长期利率与均值回复速度

(二)方差和协方差估计结果及分析

将四个利率数据序列对Vasicek模型进行回归后，将其残差带入各个多元GARCH模型中的方差方程与协方差方程，实证结果如表4。

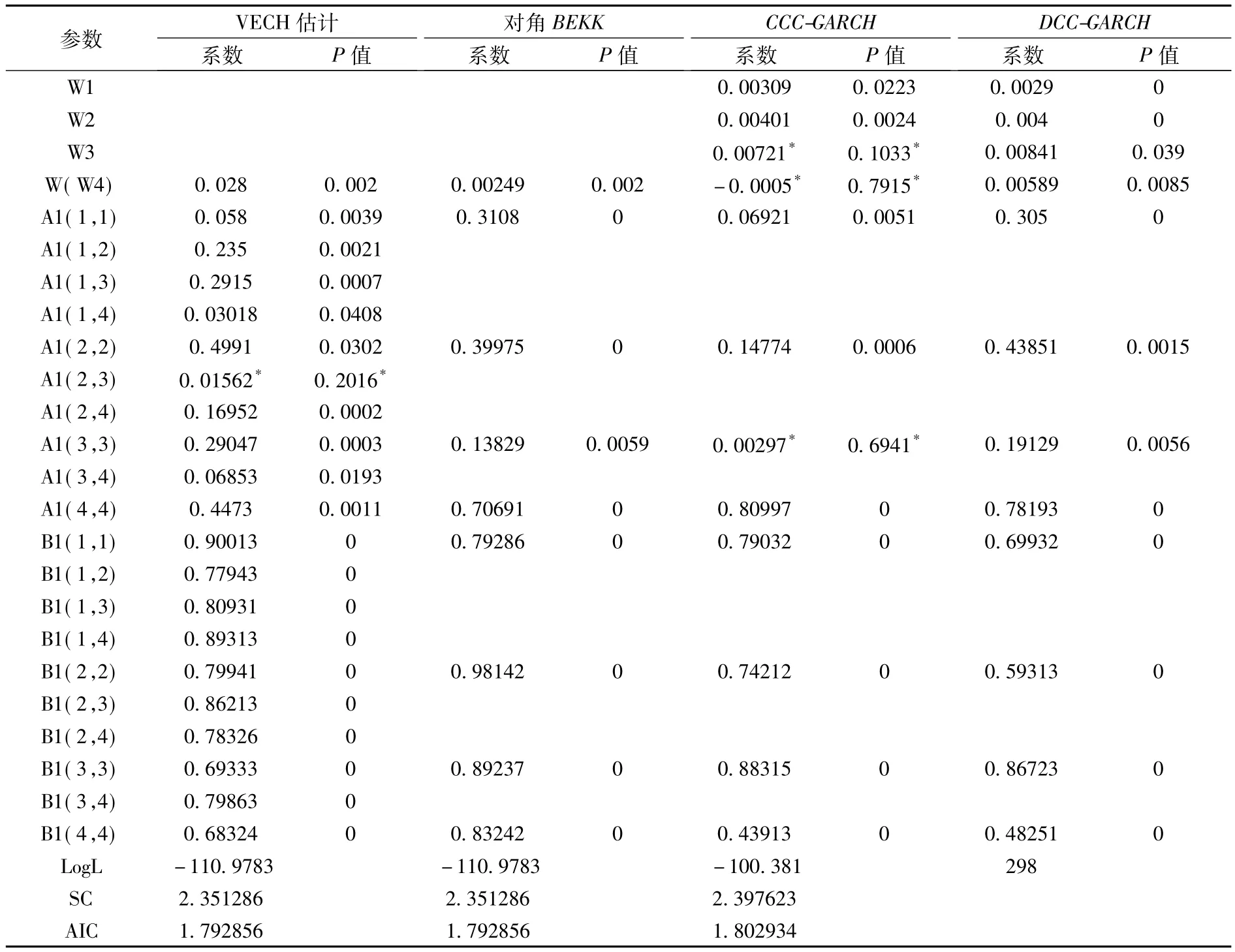
表4 方差和协方差方程估计值

1.VECH方法估计结果

运用 VECH 模型(3)式的最后一个方程进行估计，得到四个条件方差方程 h11，t、h22，t、h33，t、h44，t。在四个方程中，一天期上期残差平方项系数与方差项系数A1(1，1)为0.058，B1(1，1)为0.90013，两者之和小于1。除此之外，其余方程期限结构都大于1。这意味着在外界冲击下，利率所受到的影响存在长期的异方差效应。

得到六个条件协方差方程 h12，t、h12，t、h14，t、h23，t、h24，t、h34，t，表示各个变量之间的交互影响。得到各个方程的上期残差平方项系数和方差项系数，其中A1(1，2)为0.235，表示隔夜拆借利率和7d到期拆借利率上期残差平方之间的影响。并且每个协方差方程系数之和都接近于1，这意味着1d、7d、30d和90d拆借利率之间的影响是持久的。

2.对角BEKK方法估计结果

运用(4)式可以估计 BEKK 方法下的四个条件方差方程:h11，t、h22，t、h33，t、h44，t，且每个方程上期残差平方与方差项的系数之和均大于1，表明其存在长期的异方差效应。比较而言，两者之和要大于VECH方法对应项目，这说明BEKK方法利率间的影响更为持久。

3.CCC-GARCH方法估计结果

由方差方程(5)式得到 CCC 方法下的四个条件方差方程:h11，t、h22，t、h33，t、h44，t。表 4 中加“*”的系数从P值来看其参数未能在5%的置信水平下拒绝原假设为零的假设。这说明90天期利率方差方程中，信息项和常数项显著为0。

综上，表4实证对比表明，一是外界冲击对各期利率带来了显著的长期异方差效应;二是矩阵A系数相对矩阵B偏小，表明信息项对方差方程的影响要弱于衰减项。三是前三种方法各估计值之间的差异比较小，而从P值来看，CCC方法对90d数据序列估计中，常数项和信息项显著为0。四是VECH、对角BEKK和CCC方法在最大似然估计值、SC和AIC等方面结果基本一致，但DCC方法最大似然值显著偏高，这说明DCC方法与其他方法相比，能提高方差方程估计的有效性。

(三)相关关系估计结果及分析

利用CCC方法估计式(6)可计算出常系数动态相关关系，所得结果如表5所示。从表5可以看出，期限越短，相关度越高，这时市场主体可能会较好地把握市场信息，并作出较准确的判断。

表5 基于CCC-GARCH方法估计的相关系数

用极大似然估计函数(8)式对(7)式的估计结果如表6所示，其中α表示信息项，而β表示衰减项。估计结果表明在银行同业拆借市场中，不同期限利率间的协方差对市场信息有较低的敏感度，而对滞后一阶的协方差敏感度较高。因此，对于充满不确定性的银行同业拆借市场，利率的适度波动可以提高市场活跃度和流动性，但频繁而又剧烈的波动则会扭曲市场机制的作用。

表6 DCC-GARCH估计值

四、结 论

本文基于利率期限结构动态模型，对我国商业银行同业拆借市场利率期限结构的动态相关性进行了实证研究，得出结论如下:一是除90d数据序列，我国银行同业拆借市场利率数据序列波动均值回复现象显著，并且随利率期限的增加，均值回复速度加快。二是对不同方法最大似然估计值比较发现，DCC方法比VECH、对角BEKK和CCC方法表现出更好的拟合优度。三是当各期利率受到外界冲击时，存在显著的长期异方差效应，并且，不同期限利率间的协方差对市场信息有较低的敏感度，而对滞后一阶的协方差敏感度较高，这说明在充满不确定性的银行同业拆借市场，利率的适度波动可以提高市场活跃度和流动性，但频繁而又剧烈的波动则会扭曲市场机制的作用并引发利率风险，因此政府不应频繁变动以利率调整为工具的货币政策。

［1］Merton，Robert C..Theory of Rational Option Pricing［J］.The Bell Journal of Economics and Management Science，1973，4(1):141-153.

［2］Vasicek，O.An Equilibrium Characterization of the Term Structure［J］.Journal of Financial Economics，1977，5(2):177-188.

［3］谢赤，吴雄伟.基于Vasicek模型和CIR模型中的中国货币市场利率行为实证分析［J］.中国管理科学，2002，(3):23-26.

［4］林海，郑振龙.中国利率动态模型研究［J］.财经问题研究，2005，(9):45-49.

［5］严玉敏.基于Vasicek模型和CIR模型的中国利率期限结构实证研究［D］.长春:吉林大学，2009.32-35.

［6］Chan，K.C.，G.A.Karolyi，F.A.Longstaff.An Empirical Comparison of Alternative Models of the Short-Term Interest Rate ［J］.The Journal of Finance，1992，47(3):1209-1227.

［7］Brenner，Robin J.，Harjes，Richard H.and Kroner，Kenneth F.，Another Look at Models of the Short-Term Interest Rate ［J］.The Journal of Financial and Quantitative Analysis，1996，31(1):85-107.

［8］Longstaff F.A.and Schwartz E.S.Interest rate volatility and the term structure:A two-factor general equilibrium mode［J］.Journal of Finance，1992，47(4):1259-1282.

［9］Bollerslev T，Engle R.F.，Wooldridge J M.A Capital Asset Pricing Model with Time-Varying Covariances［J］.Journal of Political Economy，1988，96:116-131.

［10］Engle R.F.andK.F.Kroner.Multivariate Simultaneous Generalized ARCH ［J］.Econometric Theory，1995，11:122-150.

［11］Bollerslev T.Modeling the Coherence in Short Run Nominal Exchange Rates:A Multivariate generalized ARCH Model［J］.The Review of Economics and Statistics，1990，72:498-505.

［12］Engle R.F.，Sheppard K.Theoretical and Empirical properties of Dynamic Conditional Correlation Multivariate GARCH.Working paper.2001.

［13］洪永淼，林海.中国市场利率动态研究—基于短期国债回购利率的实证分析［J］.经济学(季刊)，2006，(2):511-532.