基于循环谱的数字信号的自动识别*

郑天堃，姚远程，秦明伟

（西南科技大学 信息工程学院，四川 绵阳 621010）

近些年来，通信信号的自动识别受到越来越多的关注和研究。其应用也随之越来越广泛，在民用方面，信号调制模式的自动识别是软件无线电接收机的基础；在军用方面，信号调制方式的识别也是电子对抗、信号干扰的核心技术之一[1-2]。

目前已经存在的信号调制识别方法主要分为两大类：基于决策理论的方法[1,3]和基于统计模式识别的方法[4]。其中基于决策理论方法，由于其需要每一个参数都有一个最优门限，并且参数提取和信号识别的顺序都会影响识别率，因此在现实应用中往往受到较多的限制。而基于统计模式识别的方法因其性能好得到了广泛应用。循环谱具有识别率高、抗干扰能力强、实用性强等优点而得到越来越多的重视。

1 谱相关分析

已知x(t)是一个均值为零的非平稳信号，则其时变自相关函数定义为∶

Rx(t;τ)具有周期性，可将其用Fourier级数展开得到∶

式中：α=m/To，且Fourier系数为∶

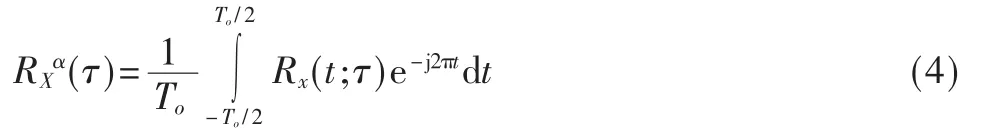
将式(2)代入式(4)，即得∶

该式中RXα(τ)被称为循环自相关函数，[·]t含义是时间平均。把使RXα(τ)≠0的频率α称为信号的循环频率，一个循环平稳信号的循环频率可能有许多个，其中包括零频率和非零频率，其中零循环频率对应的是信号的平稳部分，而非零循环平稳信号对应的信号的循环平稳部分。当α=0时，即为平稳信号的自相关函数；当α≠0时，RXα(τ)是Rx(τ)的周期加权形式，称为周期自相关函数，也称为循环自相关函数[5]。循环自相关函数RXα(τ)的Fourier变换Sxα(f)就是谱相关密度函数∶

将RXα(τ)代 入 式(6)得∶

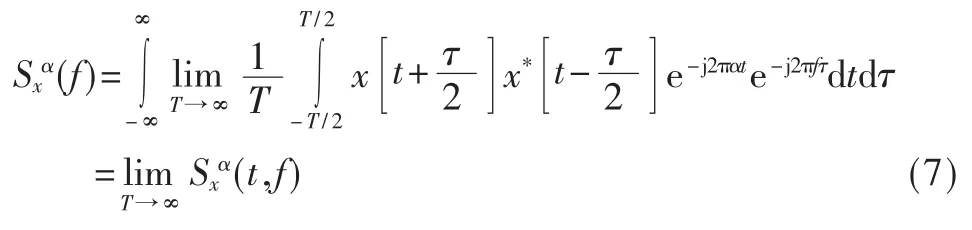
在式(7)中

前面只是陈述了谱相关密度函数的定义，而在实际仿真中计算的是离散谱相关密度函数，其计算方法可分为时域平滑法和频域平滑法[6]，本文采用频域平滑法计算信号谱相关函数，有∶

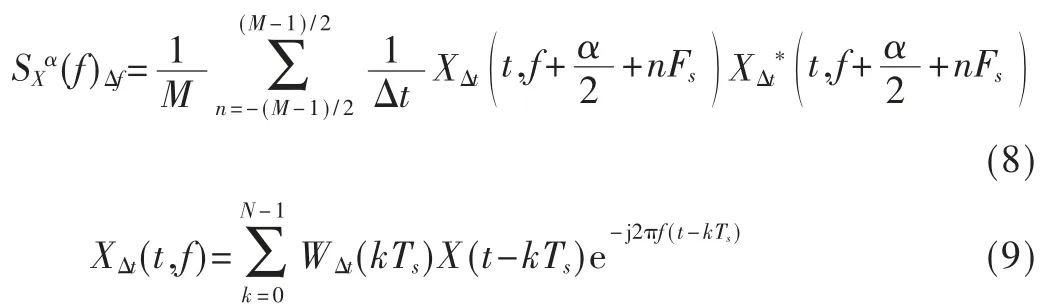
式中：WΔt(kTs)为数据窗函数;Δf=M·Fs为频域平滑宽度，M称为谱频率分辨率；Δt为数据段时间长度,则循环频率分辨率为1/Δt；Fs=1/(N-1)Ts为频率增量；N=Δt/Ts为样本长度；Ts为周期采样长度。

2 自动识别算法

根据已阅读的文献中关于数字信号识别调制的参数计算方法，以及各个参数的计算复杂程度、抗噪性的优劣，选择以下参数作为本文信号识别的参数，同时针对BPSK和QPSK识别提出一个新的参数，通过软件仿真验证该参数的优越性能。本文假定待识别的数字调制信号样集为{2ASK、4ASK、2FSK、4FSK、BPSK、QPSK}。信号识别步骤如下：

(1)以归一化后的循环谱各个轴的幅度值为分析对象，提取Sxα(0)和Sxα(fc)两个截面的循环谱幅度包络方差[7]作为识别类间的特征参数，即这两个参数可以将待识 别 的 样 集 分 为{2ASK、4ASK}、{2FSK、4FSK}、{BPSK、QPSK}。即∶

式中σi(i=1,2)分别表示Sxα(0)和Sxα(fc)两个截面循环谱幅度包络方差。其中利用参数值与参考门限值比较可以将信号集区分为{2FSK、4FSK}和{2ASK、4ASK、BPSK、QPSK}两组,利用参数M2与参考门限值t2比较可以将信号集区分为{2ASK、4ASK}和{BPSK、QPSK}两组，故利用参数M1和M2可以将待识别信号集区分为{2ASK、4ASK}、{2FSK、4FSK}、{BPSK、QPSK}。

(2)对于{2ASK、4ASK}信号，可以通过计算归一化中心瞬时幅度acn(n)绝对值的标准偏差[8-9]其定义：

图1 参数M3仿真图

(3)利用谱峰个数及幅度的不同，归一化后的2FSK和4FSK循环幅度包络的均值一定不同。所以，利用Sxα(0)截面循环谱幅度包络均值作为这两个信号识别的特征参数，即∶

在式(12)中，u是Sxα(f)截面循环谱幅度包络的均值。利用参数与门限值t4比较,如果M4＞t4，则判定该信号为2FSK，否则该信号为4FSK。参数仿真如图2所示。

图2 参数M4仿真图

从图3中可以看出，当t3=0.3时可以很好地识别出4ASK、2ASK。

图3 BPSK循环谱64点平滑三维图

从图4中可以看出，当t4=180时可以将2FSK、4FSK两种信号区分开。

图4 QPSK循环谱64点平滑三维图

(4)对于BPSK、QPSK这两种数字调制信号的识别，在理论上是比较困难的。因为它们的功率谱密度函数十分相似，特征也比较接近，频谱峰值数都为零，Sxα(f)在f轴上的归一化最大下降值都很小。在已见到的文献中关于这两个信号识别的参数计算都较为复杂，在该文中通过分析各个信号循环谱三维图的等高线仿真图，发现有明显的差异，尤其是对于BPSK、QPSK这两个信号。利用Matlab中的函数contour对信号循环谱进行观察，记参数M5为截面图中圆点个数。它们的循环谱三维图如图3、图4所示，图5、图6是利用函数contour画出截面图。

从图5、图6中可以看到BPSK、QPSK两个调制信号识别的特征参数M5有明显差别。当M5=4时，可以判定该信号为BPSK，当M5=2时可以判定该信号为QPSK。

图5 BPSK信号三维循环横截面图

图6 QPSK信号三维循环横截面图

3 性能分析

本文的系统软件仿真是在MATLAB 2011环境下完成 的，以{2ASK、4ASK、2FSK、4FSK、BPSK、QPSK}等6种调制类型。仿真时设定调制信号的载频为200 kHz，码元速率为10 KB/s，噪声采用高斯白噪声,采样频率为800 kHz，每个采样信号段内包括Ns=1 024个采样点数据，仿真时对每一个调制信号类型在信噪比-5 dB～25 dB范围内每隔5 dB产生30个样本进行仿真识别。调制识别的仿真结果由表1所示。在信噪比15 dB以上，信号自动识别率达到96%以上，同时在信噪比10 dB时，总体识别率还能达到93%，与参考文献[9]相比识别率得到了一定的提高,尤其是对于BPSK、QPSK这两种信号的识别率。

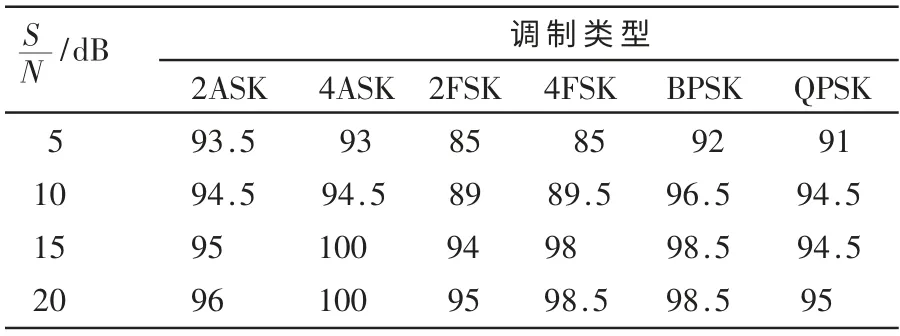
表1 常见数字信号调制类型自动识别仿真结果（%）

本文主要讨论了利用谱相关对常见数字调制信号的识别方法，尤其是BPSK、QPSK之间的识别率得到了明显的提升。谱相关是广义的周期平稳（自相关周期平稳）过程的一个特征属性，而谱相关函数是常规功率谱密度函数的推广，功率谱密度只是谱相关函数理论的一个特例。采用谱相关法对信号进行识别，最重要的是特征参数的选取，其稳定性、抗噪性、计算难易度都是识别过程中的难点和重点，这些都需要进一步深入研究，如何提高程序运行速度同时减少循环谱运算量等方面都需要进一步优化，这对实时识别都是很有实用意义的研究方向。

[1]AZZOUZ E E,NANDI A K.Automatic identification of digital modulation type[J].Signal Processing,1995,47(1)∶55-69.

[2]王洁,陈惠民,张金艺,等.数字调制方式的识别研究[J].上海大学学报(自然科学版),2002,8(3)∶197-199.

[3]SOLIMAN S S,HSUE S.Signal classification using statistical moments[J].IEEE Transactions on Communications,1992,40(5)∶908-916.

[4]NANDI A K,AZZOUZ E E.Modulation recognition using artificial neural networks[J].Signal Processing,1997,56(3)∶165-175.

[5]张贤达,保铮.非平稳信号分析与处理[M].北京∶国防工业出版社,1999.

[6]GARDNER W A,SOONER C M.Cyclic-spectral Analysis for signal detection and modulation recognition[M].IEEE,1988∶419-424.

[7]朱雷，程汉文，吴乐南.利用循环谱和参数统计的数字信号识别法[J].应用科学学报，2009,27(2)∶138-143.

[8]吕杰，张胜付，邵伟华，等.数字通信信号自动识别的谱相关方法[J].南京理工大学学报，1999,23(4)∶298-300.

[9]李俊俊，陆明泉，冯振明.一种改进的数字信号自动识别方法[J].系统技术与电子技术，2005，7(12)∶2024-2050.