刀轨环无跳刀尖角垂线过渡连接算法

杨 峰 廖文和 戴 宁 张长东 郭保苏 孙玉春

1.南京航空航天大学，南京，210016 2.上海电力学院，上海，200090 3.北京大学口腔医学院，北京，100081

0 引言

随着科学与技术的飞速发展，计算机辅助设计与制造（CAD／CAM）技术在航空航天、汽车等领域的应用越来越广泛。这些领域中需要加工的多为复杂型腔零件，零件的内部往往存在一个或多个岛屿，因此环切不失为一种较好的加工选择。环切刀轨的产生主要包括两步：刀轨环的生成和刀轨环的连接［1－2］。刀轨环生成后是相互独立的，直接加工会产生大量对实际加工没有作用的走刀（如快速抬刀、快速下刀、快速移动），影响加工效率，并且刀具的频繁跳刀与突进会在被加工模型的切削表面留下刀痕，影响加工质量和刀具寿命，因此刀轨环如何高效地连接成环切刀轨显得尤为重要［3］。

目前国内外对刀轨环过渡连接的研究主要分为两类。第一类是刀轨环几何关系的构建。Guyder［2］将刀轨连接看作是刀轨环的排序问题，其算法过于简化，适用范围有一定的局限性。Park等［4］在构建刀轨环的同时生成多根节点刀轨树，算法计算效率高，但是当刀轨环的最大等距层数为n时，会产生n－1次的跳刀。文献［5］中把多根节点树转化为单根节点结构，实现了无跳刀连接，但是刀轨树的转化需要额外计算，增加了算法复杂度。Hao等［6］提出基于“刀轨环向量”遍历刀轨环关系树的方法，该方法可以实现无跳刀，但向量的维数会随着等距环的个数增加，造成更多冗余的向量空间。张鸣等［7］构建了一种称之为区域树的树型数据结构，能够显著减少跳刀次数但并不能总是实现无跳刀。Castelino等［8］为了减小刀轨总长度，引入旅行商问题，但是该方法仅适用于每个节点只遍历一次，而且退刀点和下刀点重合的场合。第二类是过渡点连接方式的优化。Kim等［9］通过计算父子关系环之间距离最小的点把两个环连接起来，没有从几何角度考虑下刀起点的位置。Hinduja等［10］提出了基于Voronoi图刀轨环过渡的7个准则及刀轨优劣评价标准，综合考虑了加工中的几何因素和物理因素，但其生成的刀轨还需要进一步优化才能用于实际加工中。

本文提出一种刀轨环过渡连接算法，该算法基于子域构造区域等距环，根据环的等距关系构建刀轨环数组，进而生成单根节点关系树，并根据树中叶子环上点的尖角大小确定过渡点的位置，遍历刀轨环树实现无跳刀环切刀轨，最后通过实例验证了该算法的有效性。

1 刀轨环过渡连接算法基本流程

刀轨环过渡连接算法基本流程如图1所示。首先进行等距环的生成，输入边界轮廓并对其上的离散点进行基于累积曲率的简化、光顺处理，通过计算边界元素的角分线向量，把平面域边界轮廓分解为隶属于每个边界元素的子区域，进而基于子域生成等距环。然后进入本文算法的核心部分（图1虚线框部分），即实现尖角垂线过渡无跳刀刀轨。首先把生成的等距环根据等距关系构建刀轨环数组，并根据数组中环的关系建立单根节点刀轨环树，然后通过叶环上尖点垂线过渡的方式连接刀轨环，最后生成无跳刀环切刀轨。

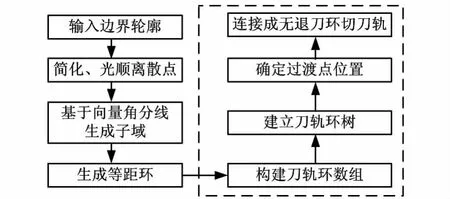
图1 刀轨环过渡连接算法流程图

2 基于子域等距的刀轨环树生成

2.1 基于子域构造等距环

边界轮廓的子域定义为隶属于每个边界元素的独立子区域，子域的内部节点是至少与边界轮廓的三条边界元素（或边界的延长线）相切圆的圆心，每条边界元素的等距线完全在其子域内产生。先对离散刀轨环进行子域分割（图2a），再根据给定的等距距离，就可生成离散刀轨环的等距线，如图2b所示。每个等距环都是多边形，由相同等距距离的等距线依次连接而成，如图2c所示。

2.2 刀轨环数组的建立

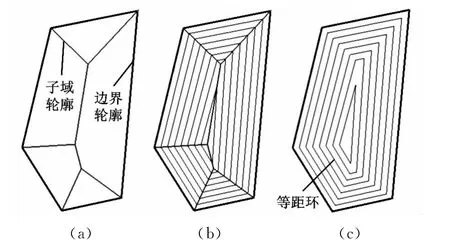
图2 基于子域生成等距线

如图3a所示，3个封闭环分别为被加工对象的边界轮廓，等距过程中，约定内环的方向为顺时针，外环的方向为逆时针。图3b中的内部环是基于子域生成的等距环。边界轮廓和等距环统称刀轨环。刀轨环之间具有嵌套关系，本算法用数组表示刀轨环，并规定逆时针方向的等距环为外等距环，顺时针方向的等距环为内等距环。

本文参考文献［6］定义了环的父子关系，即：当沿逆时针走刀路环Li行进时，如果刀路环Lj在左边，且Li与Lj至少在一段区域内相邻（即两者之间没有其他刀路环，两环之间的距离为ρ），则称Li是Lj的父环。

刀轨环数组定义格式如下：

Struct Loop

｛

bool clockwise；

unsigned offsetnumber；

Loop＃PParent；

bool isvisited；

｝

其中，数组的第一个元素表示刀轨环的方向，如果该方向是逆时针则说明是外等距环（或外边界轮廓），值为0；如果该方向是顺时针则说明是内等距环（或内边界轮廓），值为1。第二个元素表示等距环的等距次数，该值在等距过程中已经记录，边界轮廓的等距值默认为0。第三个元素指向当前环的父环。第四个元素表示在生成刀轨环关系树中是不是被遍历过。图3c所示的各刀轨环用数组表示如下：

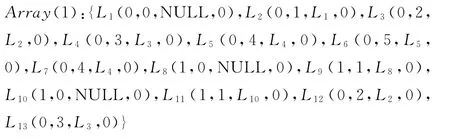
2.3 基于单向链表的刀轨环关系树的生成

2.3.1 基于刀轨环数组编制单向链表

刀轨环关系树实际是一个多向链表，本算法先根据刀轨环数组建立多个单向链表Listm（m的初始值设为1），然后生成多向链表List。刀轨环单向链表生成的具体步骤如下：

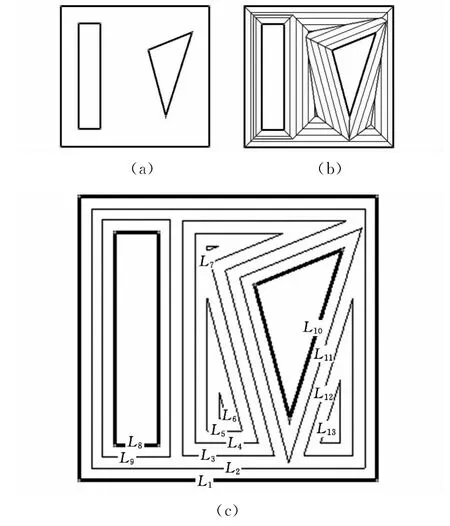
图3 等距环拓扑关系构建

（1）在 Array（1）中查找 max（offsetnumber）的环Li，并把Li作为当前环（CurrentLoop，CL），即CL＝Li且CL存入Listm中，CL.isvisited＝1；

（2）If（CL.PParent！＝NULL）｛

转步骤（3）｝Else｛

转步骤（4）｝；

（3）While（CL.PParent.isvisited＝＝0）｛

CL＝CL.PParent；

CL存入Listm中，CL.isvisited＝1；

转入步骤（2）｝；

（4）CL＝CL.PParent；

CL存入Listm中，CL.isvisited＝1；

m←m＋1；

转入步骤（1）；

（5）If（所有刀轨环的isvisited＝＝1）

单向链表构建结束。

图3c所示的刀轨环单向链表生成结果如表1所示。

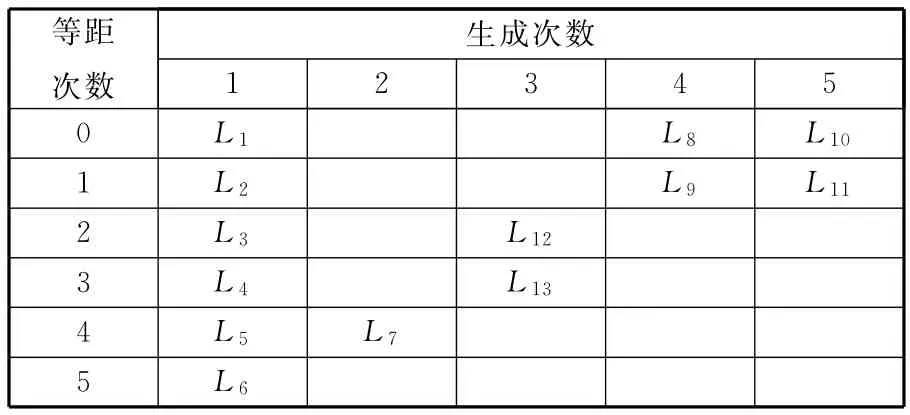
表1 刀轨环单向链表生成

2.3.2 刀轨环多向链表的构建

刀轨环关系树的生成过程即为多个单向链表生成一个多向链表的过程。根据本算法中等距环方向的规定，内等距环的等距边全部由内环等距得到，所以内等距环组成的等距环链表个数等于内边界轮廓环的个数。

本算法在单向链表中通过顺序取外等距环、逆序取内等距环的方法，最终得到单根节点刀轨环关系树，具体流程如图4所示。由于单向链表是根据环的等距次数生成的，所以首先把等距次数最大即第一个生成的单向链表构建成刀轨环主干树。按照表1中的第一个单向链表生成主干树（图5a），然后查找当前环的父环，再分别按照顺序、逆序把其他单向链表插入到主干树中，最终生成单根节点多向链表即刀轨环关系树。图5b所示为顺序插入外等距环的结果，图5c所示为在图5b的基础上逆序插入内等距环的结果。

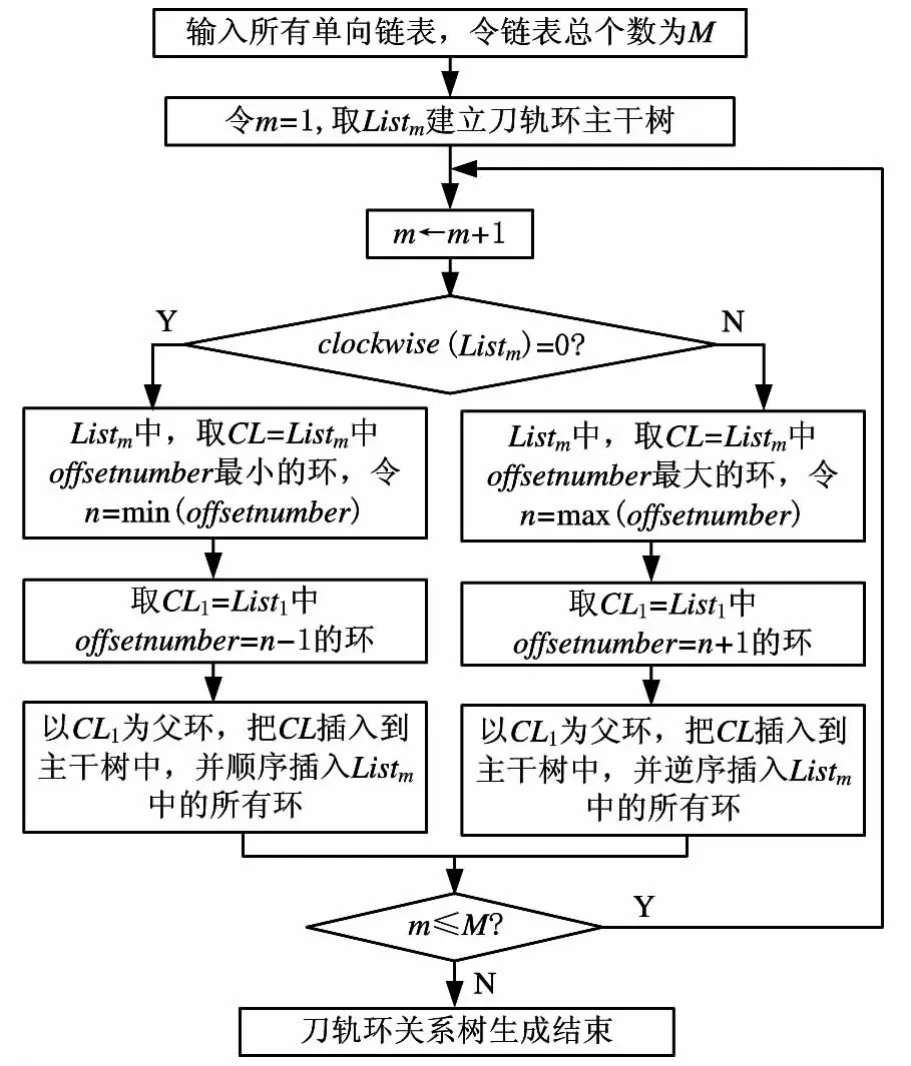
图4 刀轨环关系树生成流程图

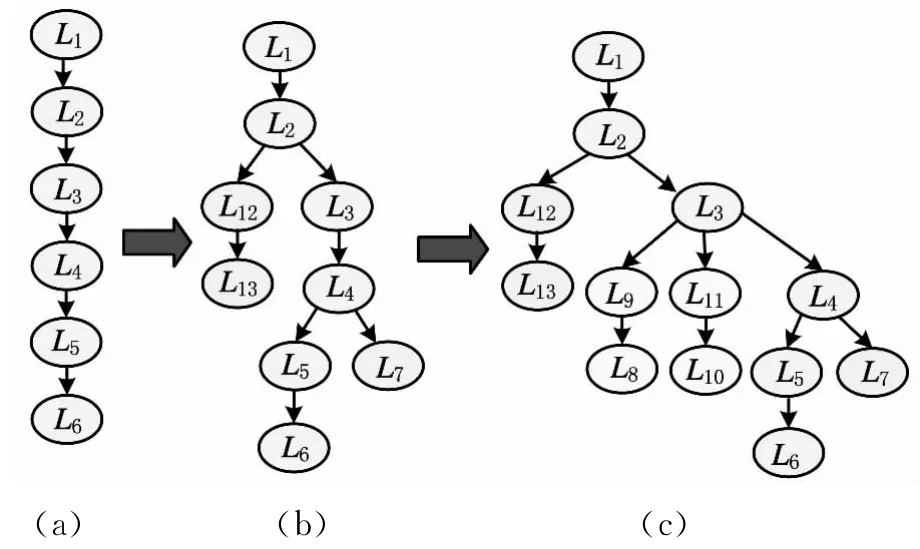
图5 刀轨环关系树生成示意图

3 尖角垂线过渡点的计算及刀轨连接

3.1 尖角垂线过渡点

过渡点是刀具从一个刀轨环过渡到另一个刀轨环的位置，过渡点位置的确定对实际加工有着重要影响。在没有优化的刀轨中，应用于子域刀轨环的过渡点主要分为三类，如图6所示。以子域角分线顶点作为过渡点，通过子域边界实现刀轨环连接，这些过渡点数据结构建立简单，但会使刀轨增加更多的尖角过渡，如图6a所示；在刀轨环上任取一点，作其相邻等距环的垂线，这种过渡方式能保证刀轨总长度最短，如图6b所示；本算法提出如图6c所示的过渡点计算方法，该方法以减少刀轨中的尖角过渡为目的，在保证刀轨总长度最短的前提下，通过计算实现尖角垂线过渡。

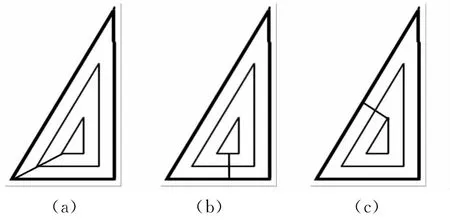
图6 过渡点位置的种类

3.2 基于离散曲率的过渡点计算

由于刀轨环由一系列离散点依次相连而成，本算法引入离散曲率确定各刀轨环尖角过渡点的位置，把曲率计算转化为三角形内边的计算，具体实现方法如下：圆逼近法求曲率是用通过相邻三个 点 Pi－1（xi－1，yi－1）、Pi（xi，yi）、Pi＋1（xi＋1，yi＋1）的圆来近似Pi点的密切圆的，如图7所示，圆的曲率Ki为

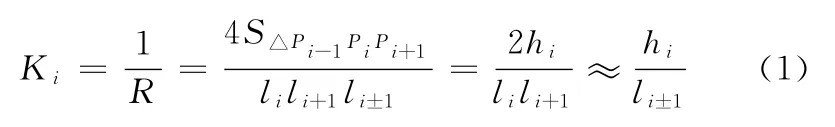
式中，R 为圆的半径；S△Pi－1PiPi＋1为相邻三个点组成的三角形面积；li为点Pi和点Pi－1之间的距离；li±1为点Pi＋1和 点 Pi－1之间的距离；hi为 点 Pi到 对 边 Pi－1Pi＋1的距离。

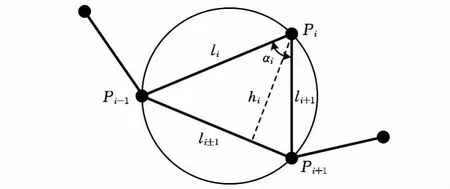
图7 点的离散曲率计算

式（1）中hi的计算公式为

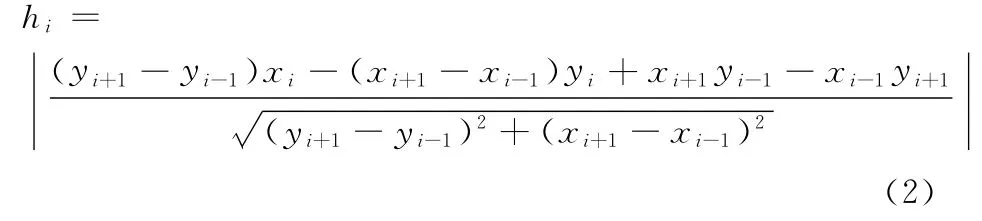
3.3 环切无跳刀刀轨的生成

通过计算刀轨环关系树中叶子环的离散曲率，取最大者即尖角位置，作其到树中父环的垂线段且垂线段的长度等于等距距离。若找不到满足条件的垂线段，则选取离散曲率次之的尖角点。同时根据树中环的父子关系建立过渡点间的父子关系。最后根据过渡点之间的父子关系实现无跳刀刀轨的生成，伪代码如下：

（1）关系树中根节点对应的等距环上任取一点作为刀轨的起始点（StartPoint，SP），当前刀轨点（CurrentPoint，CP），CP ＝IP，转步骤（2）；

（2）If（CP 是过渡点）｛

转步骤（4）｝Else｛

转步骤（3）｝；

（3）While（CP 不是过渡点）｛

CP－＞isvisited＝1；

沿着当前刀轨环环中下一个刀轨元素（NextPoint，NP）：CP ＝CPNP；

｝

If（CP！ ＝SP）｛

转步骤（4）｝Else｛

转步骤（7）｝；

（4）If（所有刀轨环的刀轨点都已被访问）｛

转步骤（7）｝Else｛

If（CP.isvisited ＝＝0）｛

步骤（5）｝Else｛

If（CP.son！ ＝ NULL）｛

转步骤（5）｝｝Else｛

转步骤（6）｝

｝；

（5）CP.isvisited ＝1；CP ＝CP.son；转步骤（2）；

（6）CP.isvisited＝1；CP＝CP.father；转步骤（2）；

（7）刀轨连接完成。

4 实例与验证

算法通过直线加减速关系图建立CNC系统中的数学模型，验证尖角垂线过渡对加工时间的影响。以图8a～图8c所示的三个轮廓的等距环为试验对象，分别生成相应的角分线（图8d～图8f）、垂线（图8g～图8i），以及本文提出的尖角垂线（图8j～图8l）来进行过渡，再将生成的无跳刀刀轨输入北京精雕JDPaintV5.50计算路径总长度，并取进给速度为2m／min，变速系数为50，分别计算三种过渡方式下的加工时间，结果如表2所示。可以看出，角分线过渡的刀轨总长度最大，加工时间最长，而垂线过渡和尖角垂线过渡的刀轨总长度相同，由于垂线过渡增大了刀具轨迹中的尖角从而增大了加减速影响，所以后者的加工时间明显短于前者。可见，在综合考虑刀轨总长度最短和加工时间最短的前提下，尖角垂线过渡优于角分线过渡和垂线过渡。

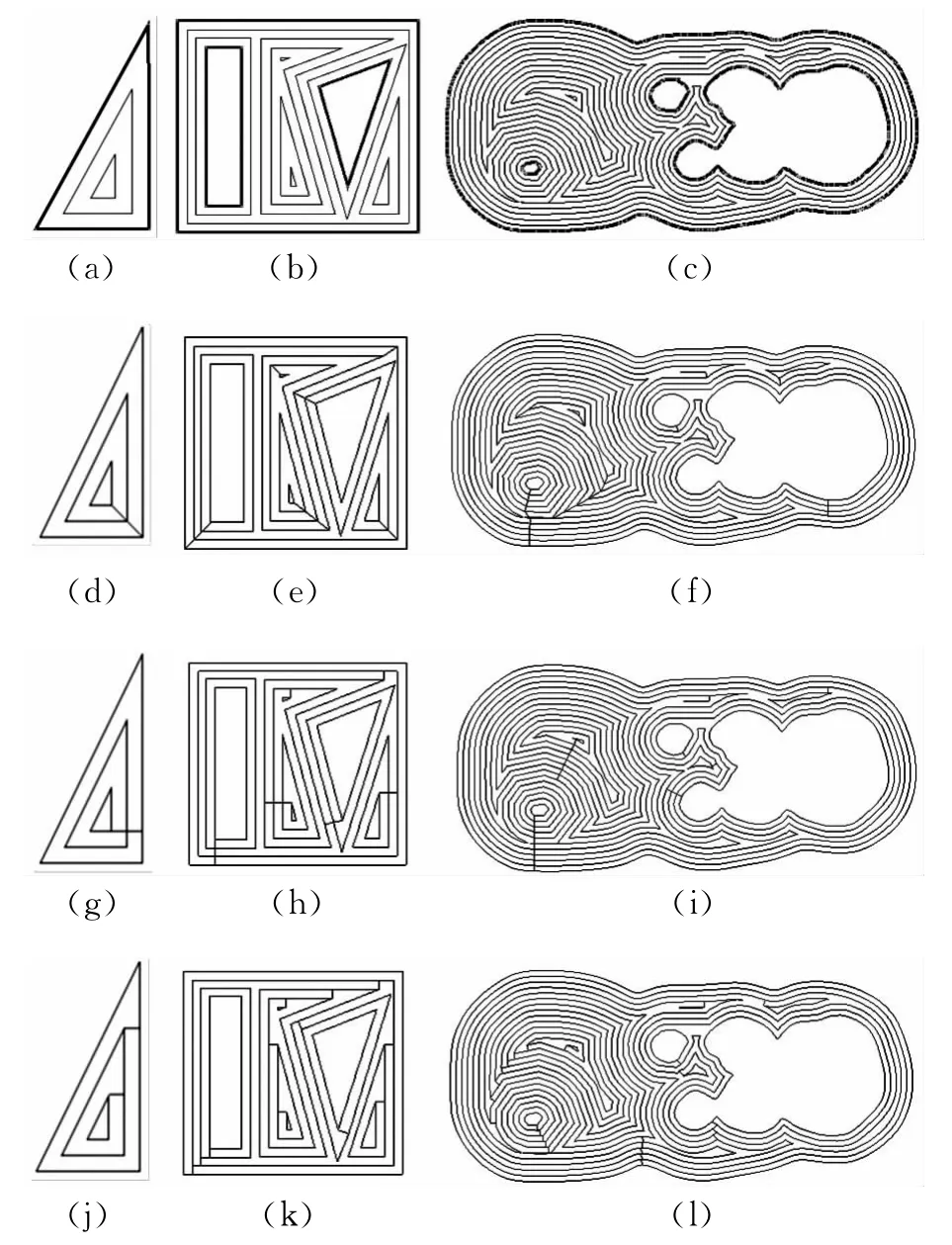
图8 过渡方式验证实例

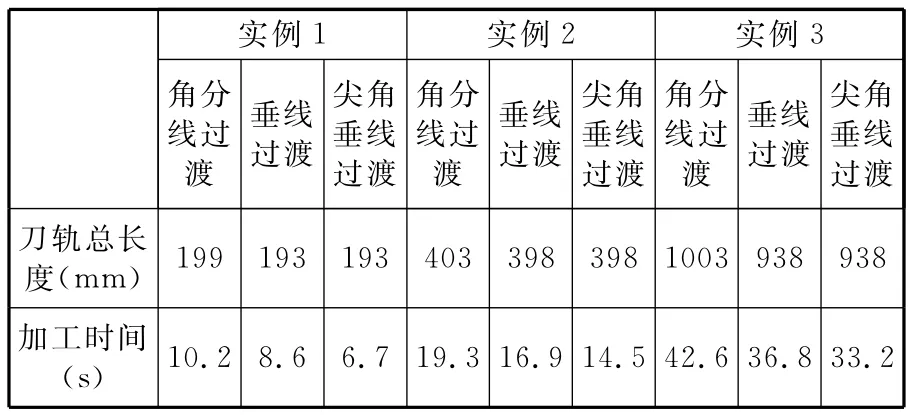
表2 过渡方式对比结果

5 结语

本文以基于子域的等距环为研究对象，提出环切无跳刀过渡连接算法。本算法特点如下：

（1）刀轨环关系树构建简单。采用基于子域的等距策略采用逆序生成内等距环、顺序生成外等距环的方式把单向链表中环加入主干关系树中，简化计算复杂度。整个算法的数据结构简单，意义明晰。

（2）以叶子环的尖点作为过渡点，缩短了实际加工过程中的加减速时间。以等距次数为关键字生成单向链表，保证了关系树中主干树中的刀轨环个数最多，从而保证了过渡连接线段位于同一直线方向上。

（3）实现了无跳刀过渡连接，仿真中没有过切现象。

［1］Choi B K，Park S C.A Pair－wise Offset Algo－rithm for 2DPoint－sequence Curve［J］.Computer－Aided Design，1999，31（12）：735－745.

［2］Guyder M K.Automating the Optimization of 2 1／2 Axis Milling［J］.Computers in Ind.，1990，15（3）：163－168.

［3］安鲁陵，周来水，庄海军，等.型腔高速铣削刀轨生成算法研究［J］.计算机辅助设计与图形学学报，2004，16（9）：1202－1206.An Luling，Zhou Laishui，Zhuang Haijun，et al.Tool Path Generation for High－Speed Milling of Pocket［J］.Journal of Computer Aided Design ＆Computer Graphics，2004，16（9）：1202－1206.

［4］Park S C，Chung Y C.Offset Tool－path Linking for Pocket Machining［J］.Computer－Aided Design，2002，34（4）：299－308.

［5］Park S C，Chung Y C，Choi B K.Contour Parallel Offset Machining Without Tool－retractions［J］.Computer－Aided Design，2003，35（9）：841－849.

［6］Hao Y T，Jiang L L.Optimal Algorithm for no Tool－retractions Contour－parallel Offset Toolpath Linking［J］.Journal of Mechanical Engineering，2007，20（2）：21－25.

［7］张鸣，刘伟军，卞宏友.基于自由区域的环切轨迹优化连接方法［J］.中国机械工程，2011，22（4）：468－473.Zhang Ming，Liu Weijun，Bian Hongyou.Optimized Contour－parallel Offset Tool－path Linking Method Based on Free Region［J］.China Mechanical Engineering，2011，22（4）：468－473.

［8］Castelino K，D’Souza R，Wright P K.Tool Path Optimization for Minimizing Airtime during Machining［J］.J.Mfg.Systems，2003，22（3）：173－180.

［9］Kim H C.Tool Path Generation for Contour Parallel Milling with Incomplete Mesh Model［J］.International Journal of Advanced Manufacturing Technology，2010，48（5／8）：443－454.

［10］Hinduja S，Mansor M S A，Owodunni O O.Voronoi－diagram－based Linking of Contour－parallel Tool Paths for Two－and－a－half－dimensional Closedpocket Machining［J］.Proc.IMech.，Part B：Journal of Engineering Manufacture，2010，224（9）：1329－1350.