面向系统的平面公差语义及其数学模型

黄 强 张根保 王 健

1.重庆理工大学，重庆，400054 2.重庆大学，重庆，400044 3.四川普什宁江机床有限公司，都江堰，611830

0 引言

机械产品的公差设计质量是影响其功能、质量及成本的决定性因素［1］。随着计算机辅助公差设计（CAT）的出现和发展，利用计算机建模进行公差分析、公差综合以及公差优化的研究和应用工作已在国际范围内展开并取得了显著的成效。在这些研究与应用中，各种公差建模思想和表示形式在不同的应用目标下各有所长［2－7］。在现代企业中，CAD／CAE／CAPP／CAM 已逐步趋于集成。为了与企业现有产品开发系统相适应，国内针对三维造型体的公差建模研究也逐渐增多，这类建模主要基于数学定义或小位移旋量［8－10］。产品的公差设计是面向功能的设计。目前，面向功能的公差设计研究往往以可装配性为目标。在机床精度设计中，机床输出精度是一项必须保障的最终功能目标。机床系统的最终输出精度在很大程度上取决于机床零部件的公差设计，在零部件的公差语义中增加对系统精度的作用属性，就可以通过数字化方法分析相关公差项目对系统精度的约束效应，为机床公差设计提供直接依据。基于这一目标，本文以机床总装中最常见的安装接触表面——平面要素为例，分析并完善其在装配系统中的公差语义，并建立对应的数学模型。

1 对TTRS的公差语义需求

1.1 需求分析

零件由各种类型的表面围成，这些表面的不同功用决定了它们加工要求的不同。Bourbet于1987年提出了“与工艺和拓扑相关表面”（topologically and technologically related surface，TTRS）的概念，之后逐步发展成为目前较为成熟且应用广泛的一种公差表示方法。TTRS的定义如下：一个TTRS是同一实体上因功能原因而彼此联系的表面。因此，应用TTRS理论可较好地表示零件层面的公差信息，也为在装配层面中确定与该零件相关的公差拓扑关系提供了条件。在对系统精度的定量分析及公差设计中，还存在对基于TTRS的公差语义及其数学模型新的需求。下面举例说明。

图1为某机床结构示意图，为叙述简明，图中略去部分部件如工作台、导轨等。下标1、2、3、4分别表示床身、立柱、主轴箱及主轴，相邻部件的接触此处视为广义配合。在整机层公差设计中，将每一个部件视为一个误差单元，即公差控制对象。其公差数字化分析及设计的简要方案如图2所示。

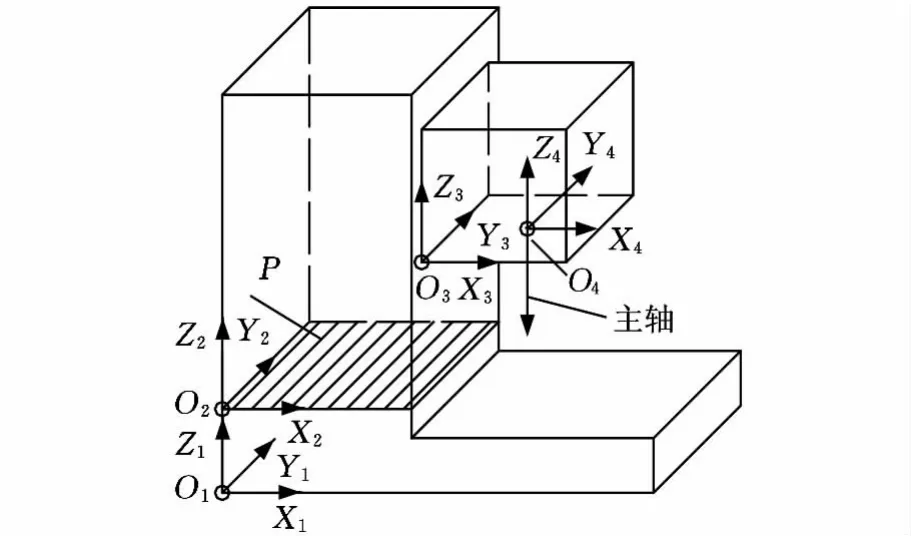
图1 某机床结构简图

图2 机床系统精度分析及公差设计方案简图

（1）建立机床在整机层面上的数字化误差模型。机床误差建模基于多体系统运动学理论和齐次坐标变换原理［11］，在装配层面上，模型能准确反映机床各个部件之间的几何位置、姿势、运动关系以及误差传递规律。该模型是计算机辅助系统精度分析及公差设计的核心，将用于机床误差单元的敏感性分析、公差控制效果的数字化检验以及单项公差对系统输出精度的作用规律分析。

（2）机床误差单元的敏感性分析。应用前述模型，通过对误差单元的六自由度误差进行单位误差设定，可以预测分析各个误差单元对机床输出误差的影响权重，尤其是在加工误差敏感方向上的影响权重，从而为机床整机的公差分配及装配调整提供重要依据。详细的建模、分析方法以及对具体样机的分析示例可参阅文献［12］。

（3）公差制定。在该层面上，只对各个部件中的部分TTRS进行公差限定，即针对影响机床整机输出精度的装配结合面。限于目前计算机智能及推理能力的发展水平，公差类型主要采用人工制定，如床身－立柱安装面与工作台－导轨安装面之间的平行度、主轴轴线与主轴箱主轴输出端面的垂直度等。确定这些公差大小的依据来源于以下三个方面：①误差敏感性分析结果，越敏感的误差制定越严格的公差；②企业现有工艺和加工设备的精度保障能力；③企业的公差设计经验沉淀。

（4）公差控制效果检验及公差调整。在完成公差的初步制定后，其控制效果是否满足设计要求是未知的，必须对各项相关公差的积累控制效果进行数字化预测检验。如果预测检验的结果不合格或者不理想，就需要结合敏感性分析的结果选择公差调整对象并进行针对性的调整，而确定调整量大小，则需要先分析该项公差对系统输出精度的量化作用规律。这是一项人机交互式的循环工作，直到设计结果满意为止。要完成这两项工作，都需要相关TTRS的公差具有面向系统的语义及与之对应的数学模型。

1.2 TTRS的公差语义范畴

上述需求分析表明，TTRS的公差语义应涵盖两个层面：

（1）零件层。零件层公差语义表达零件的自身属性，即描述公差的原始定义，主要用于零件的加工工艺编制及检验等工作，此处不再赘述。

（2）装配层。装配层公差语义表达该零件作为系统的一个环节而具有的属性，即在系统中对其广义配合件的作用输出，因此也可称之为对外作用语义。例如，设图1中床身与立柱的结合表面为P，其公差为TP，则该公差的零件层语义是该平面的最大允许变动范围和方向。在功能层面或者说装配层面上，该公差所控制的误差对最终执行主轴的作用效果，是在系统精度分析及公差设计中必须掌握的关键要素。平面P在公差范围内的变动，通过部件2、3传递到主轴4，并最终导致主轴4偏离理论位置和姿势（简称位姿）而影响机床功能。公差TP的直接作用效应是使部件2在六自由度上偏离其理想位姿，即沿X向、Y向和Z向的平移以及绕X轴、Y轴和Z轴的转动，本文用ΔX、ΔY、ΔZ、Δα、Δβ和Δγ表示，这一组输出变量可定义为公差TP的对外作用语义。

在TTRS理论中，零件的TTRS被划分为7个基本类，平面只是其中一类，本文选取机床总装中最常见的安装接触表面——平面这一要素为对象，建立和探讨其两层语义对应的数学模型。

2 平面公差的数学模型建立

2.1 建模原则

（1）“一般”到“特殊”的原则。空间直角坐标系中，平面可分为坐标面平行面、坐标面垂直面和一般位置平面三种，前两者为特殊位置平面。尽管特殊位置平面在零件中出现频率更高，但由于一般位置平面更具代表性，故建模从“一般”状态入手，“特殊”状态由“一般”状态退化而成。

（2）实用性原则。目前，零件的三维几何造型技术及应用已相当普及，而几何形体在原始造型时就携带公差信息的技术尚未进入实用阶段。为便于工程应用，公差建模基于已完成造型零件的便于捕捉的几何特征。

（3）统一性原则。平面要素尽管具有两个层面的公差语义，但其数学模型应涵盖两个层面。

（4）针对性原则。两层公差语义有不同的适用场合，模型表达形式应符合使用场合的需要。

2.2 平面的公差域及其数学表达

2.2.1 平面的公差域范畴及公差原则分析

对一个指定的平面，在不同情况下有不同的公差约束形式，如尺寸公差，相对其他要素（平面和直线）的平行度、垂直度、倾斜度、对称度以及本身的平面度。公差域由4个要素决定，平面的公差域具有相同的形状，所以不同的平面公差约束形式（项目）体现为位置、大小和方向的不同。

公差原则分成两类：独立原则和相关原则。尽管相关原则包含包容要求、最大实体要求、最小实体要求和可逆要求，但它们的公差域均是由尺寸公差和形位公差的包容或叠加而成的，可统一视为一个不同构成的公差域。独立原则由于是尺寸公差和形位公差单独约束并检验的，可划入公差模型的两次使用问题。

2.2.2 公差域的数学表达

公差域选择基于点坐标的数学表达方式。这样选的原因如下：一是三点法是最基本的一种平面表示方式；二是三维造型体中的点坐标最易捕捉。另外，在公差检验，尤其是CMM（coordinate－measuring machine）测量中，点坐标是最直接的检测量。

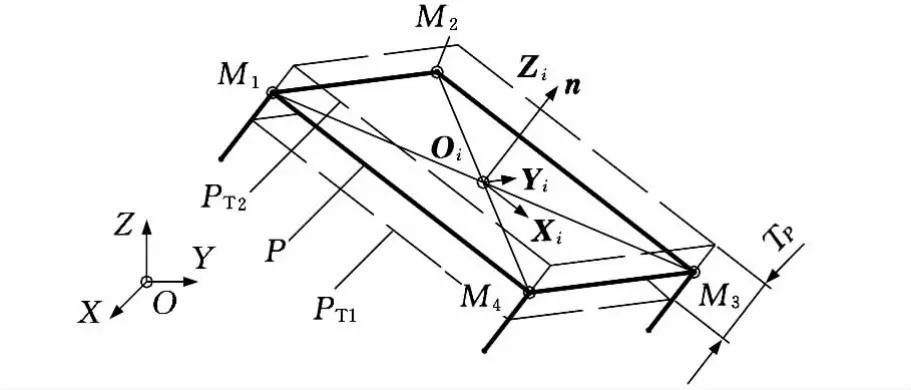
图3 平面公差的几何模型示意图

如图3所示，一空间理想平面P，其总的公差要求为TP（上下界分别为PT1和PT2），并符合如下设定：①平面具有规则形状，文中以矩形为例。平面被指定后，4个角点的坐标至少三点可捕捉（已知），其坐标为Mi（xi，yi，zi），i＝1，2，3，用于表达该平面公差域的四要素。②公差TP为平面法向n上的总公差要求，包括尺寸公差、形位公差以及公差原则。其两个极限边界的形状与平面P相同且到平面P的法向距离均为TP／2（其他情况可转换为该模式）。

平面P的方向由法向矢量表示：

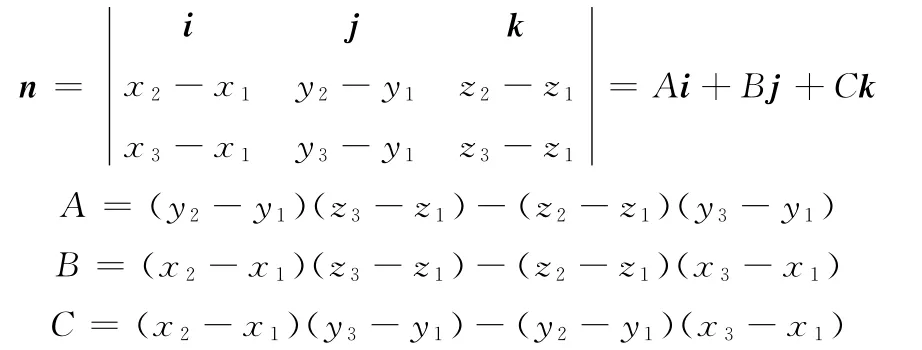
应用点法式得平面P的理想位置方程为

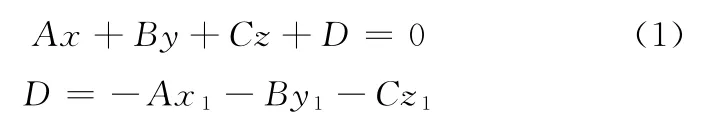
按照平面公差的原始定义：实际平面P′应包容在由理想平面P及其公差TP决定的极限平面PT1与PT2内。平面公差的检测一般基于“与理想要素相比较”的原则，在该原则下，该语义又可描述为实际平面P′上的所有点M′i（x′i，y′i，z′i）在法向n上的偏离量绝对值不超过TP／2。即

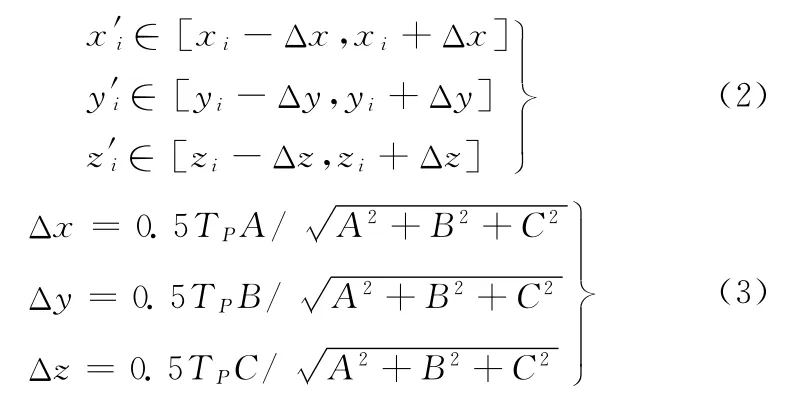
由式（1）、式（3）推导出P平面公差的两个极限（上下界）平面方程：

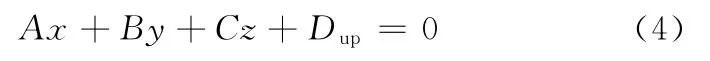
式（1）～式（5）构成了一般位置平面公差域的完整数学描述，同时也表达了该平面在零件层的公差语义，不仅可作为软件量规直接应用于平面公差的一致性检验，也为公差的对外输出特性求解提供了基础。

变动体法是一种利用底层CAD进行系统公差分析与设计的方法［7］，是实现CAD／CAT／CAM集成的一种基础解决方案。如果采用上述公差域描述形式，将更有利于变动体的高效构建。所谓高效构建变动体，是指零件表面中只有被公差约束的几何要素发生局部变动，即构造局部变形体。例如，图3零件中的平面P为公差约束表面，该零件的变动是局部的且受公差TP约束，其变动量直接体现为4个角点M1，M2，M3，M4的坐标变化，变动范围的求解分为以下两种情况：

（1）棱边与平面P垂直。直接使用式（2）、式（3）；

（2）棱边与平面P倾斜。需要进行棱边与极限平面PT1与PT2的求交运算。

2.3 平面装配层公差语义的数学表达

平面在装配层的公差语义，应准确描述平面公差对广义配合体的作用效应。直观地讲，图3中部件1的实际表面P在其上下界PT1与PT2内变动，必然导致其广义配合体2偏离理想位姿，这一位姿变化可用其局部坐标系的6个自由度变化输出描述。

2.3.1 参量求解

在6个输出参量中，三个线位移输出的最大值ΔX、ΔY和ΔZ已由式（3）得到，这里还需要补充三个转动自由度输出Δα、Δβ 和Δγ 的数学表达式。

如图3所示，在平面P的中心建立局部坐标系OiXiYiZi，Xi和Yi轴分别平行于矩形的两条边，Zi轴平行于平面法向量n。设矩形边长分别为2a和2b（也可由角点坐标差表示），在该局部坐标系内，平面法线n在公差TP范围内的最大转动偏移量为

式中，dθx、dθy和dθz分别为平面法矢量n与Xi、Yi和Zi轴的相对转动量。

从式（6）可以看出，该组参量的值取决于平面的大小及其公差，而在零件原始坐标系OXYZ中的输出值Δα、Δβ和Δγ则与平面的位姿有关，其关系如下：

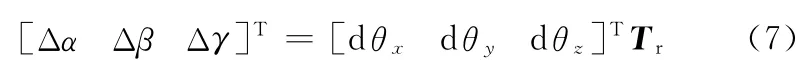
其中，Tr为局部坐标系OiXiYiZi与零件原始坐标系OXYZ之间的旋量矩阵：

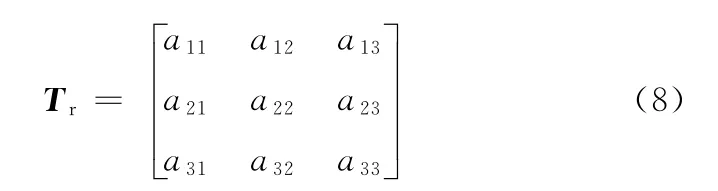
式中，aij分别为局部坐标系OiXiYiZi中三个坐标轴与零件原始坐标系OXYZ中三个坐标轴夹角的余弦。

Zi轴的矢量已在式（1）中求出，Xi轴和Yi轴矢量表达式如下：

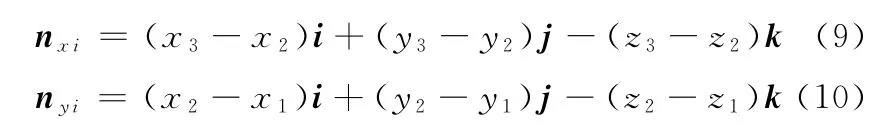
根据式（1）、式（9）和式（10）可求出式（8）中的各参量：

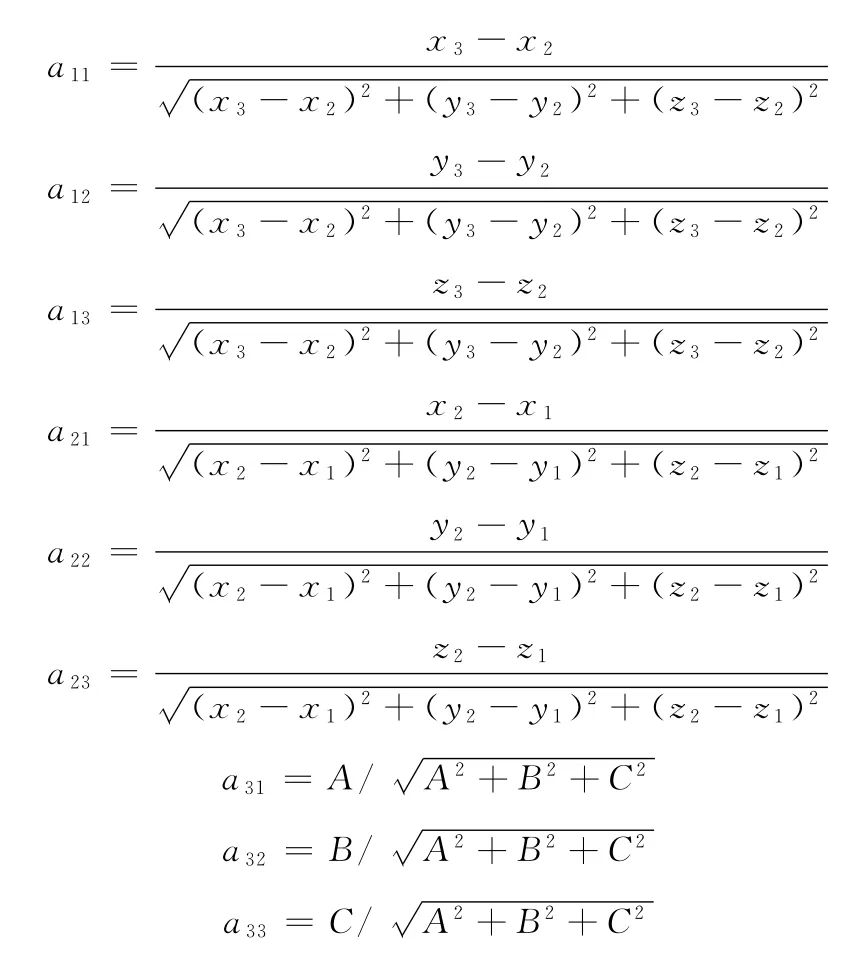
将式（6）和式（8）代入式（7）可得：

2.3.2 数学表达形式

按照“针对性原则”，公差数学模型的表达形式应符合使用场合的需要。在前述机床系统精度分析及公差设计方案中，机床误差建模基于多体系统运动学和齐次坐标变换原理，相邻体i和j之间的实际位姿变换矩阵为［11］

其中，Tij为相邻体之间的理想位姿变换矩阵，而ΔTij是两者之间的误差变换矩阵。公差用于约束指定的误差，所以在系统的三维公差分析与设计中，公差应具有与误差ΔTij一致的表达形式：

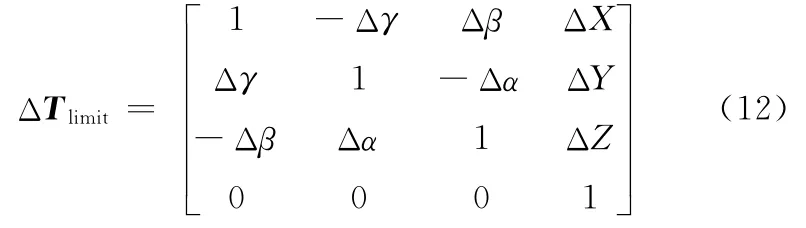
其中，三个线位移输出的极限范围已由式（2）给定；而三个转角的极限输出范围分别为。

式（12）针对性地表示了一般位置平面P在公差TP约束下对相邻体的输出特性，以下略去模型从一般位置平面退化到特殊位置平面的推导过程及结果。

3 应用示例

面向系统的公差语义及其数学模型的建立，为实施图2所示的系统数字化精度分析及公差设计方案提供了必要的支持。由于整机的公差设计效果预测（积累效应分析）包括一系列的公差项目，涉及过多的设定与分析描述，所以本文选取一个单项公差的作用规律分析作为应用示例。

图4为国内第一台基于零传动技术的高精度高效滚齿机三维装配示意图，图中工件主轴部件2安装在床身9上。图5为两者接触面以及工件主轴部件的坐标示意图，此处将床身上的该平面简称为P。工件主轴轴线应平行于轴向进给导轨（部件8和部件9之间的导轨）是机床设计的一项重要要求，床身上的平面P与轴向进给导轨安装面之间的平行度要求，是保障该项设计要求的主要因素之一。

图4 YK3610样机的三维装配示意图

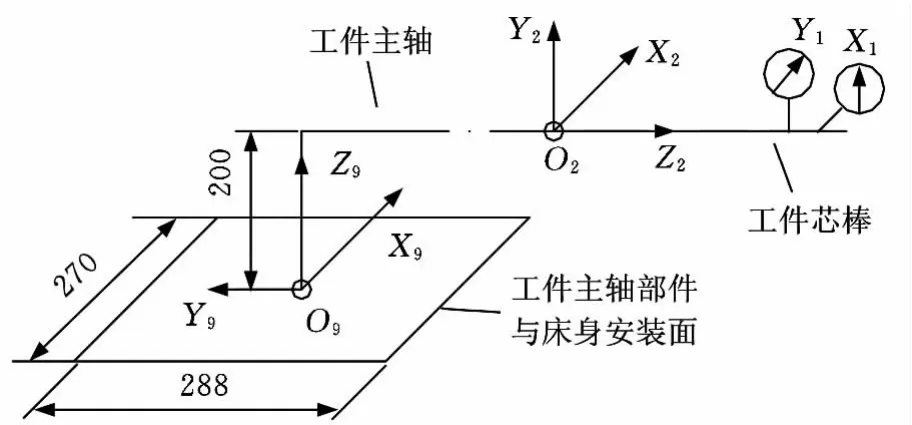
图5 工件主轴部件安装表面坐标示意图

分析目标：预测分析平面P在平行度公差TP约束下工件芯棒轴线的变动范围及规律，用图5中X1和Y1两个方向的跳动值表征。

在工件芯棒轴线上设定分析点Q（0，0，L），L的取值范围为工件安装范围。根据机床系统误差建模结果［11］，Q点到床身坐标系的传递关系为

基于这一传递关系，设此时工件主轴部件到工件芯棒之间无误差，即ΔT21为单位矩阵，再将ΔT92设为式（13）所示公差，就可以预测平面P的平行度公差TP在指定目标下的约束效果及调整量。

（1）TP的约束效果预测。设图5中X1和Y1两个方向跳动值的设计要求为300∶0.015mm。如果公差TP的初始设计值为0.02mm，P平面误差可以引起的最大跳动值如下：X1方向——0.001mm；Y1方向 ——0.0208mm。预测结果表明：如果TP＝0.02mm，即使不考虑主轴芯棒自身误差及轴向进给导轨误差的情况下，Y1方向的最大跳动值已超标，所以，TP需要调整。另外，X1方向的跳动值对TP十分不敏感，这对后续分析及今后的设计和加工十分有利。

（2）TP与作用结果之间的关系。图6是TP大小与Y1方向最大跳动值之间的映射关系；如果P平面误差在TP范围内服从正态分布，则造成的Y1方向最大跳动值的统计分布如图7所示。依据图6、图7，可反求满足要求的TP值。由于影响X1和Y1两个方向跳动值的因素包括TP、轴向进给导轨误差以及主轴芯棒自身误差等，所以TP的调整应建立在合理的精度分配基础之上。

图6 TP与Y1方向最大跳动值之间的映射关系

4 结论

（1）在机床整机层面的数字化精度分析及其公差设计中，需要零件的相关TTRS具有面向系统的公差语义，该语义可定义为该公差对其广义配合件在6个自由度上的作用输出。

图7 TP范围内Y1方向最大跳动值的统计分布

（2）基于造型特征点的平面公差域描述更有利于在零件和装配两个层面中的应用；公差的对外作用语义表示为齐次坐标变换矩阵的形式，可以将公差数学模型与系统误差模型统一起来，实现公差设计效果的数字化预测以及公差大小的针对性调整。

（3）建立公差与控制目标之间的映射关系，可以为公差大小的合理调整提供量化依据。

［1］张根保.计算机辅助公差设计综述［J］.中国机械工程，1996，7（5）：47－50.Zhang Genbao.Summary on Computer Aided Toleraning［J］.China Mechanical Engineering，1996，7（5）：47－50.

［2］Cai W.A New Tolerance Modeling and Analysis Methodology Through a Two－step Linearization with Applications in Automotive Body Assembly［J］.Journal of Manufacturing Systems，2008，27（1）：26－35.

［3］Noorul H A，Karthikeyan K，Sivakumar K，et al.Partiele Swarm Optimization（PSO）Algorithm for Optimal Machining Allocation of Clutch Assembly［J］.International Journal of Advanced Manufacturing Technology，2005，27（9）：865－869.

［4］Vignat F，Villeneuve F.Simulation of the Manufacturing Proeess（Ⅱ）：Analysis of Its Consequences on a Functional Tolerance［C］／／Proceedings of the 9th CIRP Computer Aided Tolerancing Semimear.Tempe，2005：1－15.

［5］Peng H P，Jiang X Q，Liu X J.Concurrent Optimal Allocation of Sesign and Process Tolerances for Mechanical Assemblies with Interrelated Dimension Chains［J］.International Journal of Production Research，2008，46（24）：6963－6979.

［6］Jeang A，Chung C P，Hsieh K.Simultaneous Process Mean and Process Tolerance Determination with a Symmetrical Loss Function［J］.International Journal of Advanced Manufacturing Technology，2007，31：694－704.

［7］陈善勇，李圣怡.多特征的位形空间理论及其在定向公差建模与评定中的应用［J］.机械工程学报，2005，41（9）：7－11.Chen Shanyong，Li Shengyi.Configuration Space of Multiple Features with Application to Modeling and Evaluation of Orientation Tolerances［J］.Chinese Journal of Mechanical Engineering，2005，41（9）：7－11.

［8］刘玉生.基于数学定义的平面尺寸公差数学模型［J］.机械工程学报，2001，37（9）：12－17.Liu Yusheng.Mathemathical Model of Size Tolerance for Plane Based on Mathemathical Definition［J］.Chinese Journal of Mechanical Engineering，2001，37（9）：12－17.

［9］胡洁，吴昭同，杨将新.基于旋量参数的三维公差累积的运动学模型［J］.中国机械工程，2003，14（2）：127－131.Hu Jie，Wu Zhaotong，Yang Jiangxin.Kinematic Model of 3DTolerance Accumulation Based on Screw Parameter［J］.China Mechanical Engineering，2003，14（2）：127－131.

［10］徐旭松，杨将新，曹衍龙.一种面向可装配性的公差分析方法［J］.中国机械工程，2008，19（24）：2976－2981.Xu Xusong，Yang Jiangxin，Cao Yanlong.A Tolerance Analysis Method for Feasibility of Assembly［J］.China Mechanical Engineering，2008，19（24）：2976－2981.

［11］李圣怡，戴一凡.精密和超精密机床精度建模技术［M］.长沙：国防科技大学出版社，2007.

［12］黄强，张根保，张新玉.机床位姿误差的敏感性分析［J］.机械工程学报，2009，45（6）：141－146.Huang Qiang，Zhang Genbao，Zhang Xinyu.Sensitivity Analysis of the Position－pose Error in Machine Tool［J］.Chinese Journal of Mechanical Engineering，2009，45（6）：141－146.