磁铁矿磁性物含量与TFe品位关系的数学模型

田 娟，樊民强

（太原理工大学矿业工程学院，山西 太原030024）

无论是磁铁矿的选矿试验还是生产，产品中全铁（TFe）含量的检测和分析，对最终选别指标的控制，特别是对指导生产、调节工艺参数起着至关重要的作用。目前，试验和生产中为满足分析需要，一般采用化学分析的方法，周期长，选用的重铬酸钾等滴定药剂对环境不利，且对试验或生产不能起到及时的指导作用［1］。

在重介质选煤生产实践中，磁性物含量是一项需要经常测定的指标，而在铁矿石的分选中应用较少。磁性物含量的测定简单快速，不需要苛刻的化学条件，不会对环境造成不利影响。对于能否利用磁性物含量来快速判断磁铁矿精矿品位及指导生产，本文以重选和浮选分选产品的磁性物含量测定结果及化学分析结果为基础，对磁铁矿磁性物含量和TFe品位之间的关系进行了分析研究。

1 数据

1.1 磁铁矿样品

试验样品采自太钢尖山选矿厂，对四次磁选的精矿进行重选试验，对磁选柱选别后的中矿进行浮选试验，两组试验得到的产品分别进行磁性物含量测定和TFe品位化验。

1.2 磁性物含量测定

实验室对磁性物含量的测定选用CXG－90A型磁选管［2］。根据不同磁场强度下的磁性物含量测定结果及TFe品位的化验结果（表1）可知，当提高磁场强度时，磁性物百分含量变化很小，说明该磁铁矿粉中磁性物为强磁性，连生体较少。鉴于SiO2含量随激磁电流减小略有降低，因此在低电流（0.5A）下进行全部样品的磁性物含量测定。

1.3 磁铁矿TFe品位测定

重选和浮选得到的产品送国土资源部太原矿产资源监督检测中心进行TFe品位和SiO2含量化验。采用三氯化钛还原重铬酸钾滴定法测定TFe品位（GB／T6730.65－2009），铁矿石化学分析方法中的重量法测定SiO2含量（GB／T6730.10－1986）。

1.4 数据

64组磁性物含量、TFe品位及SiO2含量的数据见表2。

表1 不同场强下磁铁矿粉磁性物含量及品位测定结果

表2 磁铁矿分选产品测定数据

TFe品位与SiO2含量都是衡量铁精矿品质的关键指标，分析确定两者的相关关系，对铁矿石的分选试验与生产具有重要意义。邓克等人的研究表明：不同的铁精矿，其中除铁矿物和SiO2以外的杂质含量具有较好的稳定性；同一选矿厂中，铁精矿的铁综合理论品位是比较稳定的，铁精矿中铁品位与SiO2含量之间存在显著的线性关系［3］。

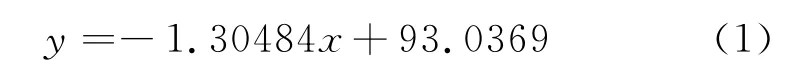
根据表2中磁铁矿分选产品的分析测定结果，对TFe品位与SiO2含量作线性回归，得到回归方程为回归相关系数R2＝0.98479，说明铁精矿中TFe品位与SiO2含量之间存在显著的线性关系，也反应了数据的可靠性。TFe品位与SiO2含量的回归结果见图1。

2 TFe品位与磁性物含量的Weibull分布数学模型

2.1 模型的建立

以TFe品位为横坐标，磁性物含量为纵坐标，绘制散点图（图2）。由于图2中TFe品位与磁性物含量之间关系曲线呈S型，不难得知，若铁矿物全部以磁性物存在，TFe品位为0时，磁性物含量应为0，随TFe品位增加，磁性物含量增加；当TFe品位逼近磁铁矿（Fe3O4）理论品位72.41%时，磁性物含量应逼近于100%，TFe品位与磁性物含量的关系具有典型的分布函数特征［4］。在众多分布函数中，Weibull分布形式简单，在矿物加工过程中，经常用于描述颗粒的粒度分布，即Rosin－Rammler方程。该分布还被用来描述旋流器分级曲线以及筛分、破碎等动力学过程［5］。

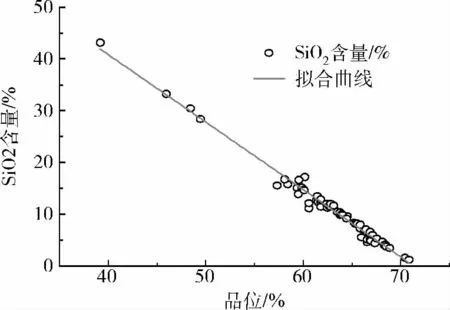
图1 磁铁矿中TFe品位与SiO2含量的相关关系

以TFe品位为横坐标，磁性物含量为纵坐标，构建两参数的Weibull分布数学模型，其表达式为

式中，P 为 TFe品位（%），取值范围为（0，72.41）；C为磁性物含量（%），取值范围为（0，100）；a，b为回归参数且均大于0。

2.2 回归精度

对于式（2），采用非线性回归方法求解模型参数，回归精度表示为

为了便于对比，对式（2）进行反函数转化，TFe品位实验值和计算值的回归精度为

σ、ε越小，说明回归精度越高，建立的数学模型越可靠。

2.3 回归结果

根据式（2）分别对表2中的全部64组试验数据及磁性物含量＞90%的52组试验数据进行曲线回归，其回归曲线见图2～图3，回归结果见表3。

由拟合曲线和回归精度可知，实验值和计算值之间具有良好的拟合精度，验证了用Weibull分布描述TFe品位与磁性物含量关系的可靠性。但从式（2）的反函数得到的铁品位的ε值仍偏高，说明回归精度较低，需对磁性物含量与TFe品位的关系进行直接研究。

图2 磁铁矿TFe品位与磁性物含量的Weibull分布曲线

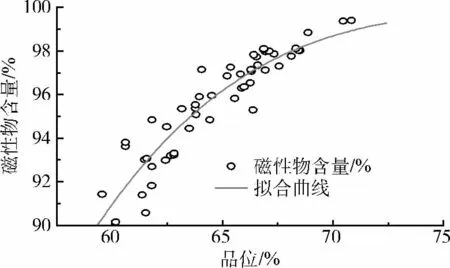
图3 高品位磁铁矿TFe品位与磁性物含量的Weibull分布曲线

表3 磁铁矿TFe品位与磁性物含量的Weibull分布回归结果

3 磁性物含量与TFe品位的对数数学模型

3.1 模型的建立

对式（2）求反函数，重新设定其中的参数，weibull分布即转化为以磁性物含量为横坐标、TFe品位为纵坐标的对数分布，其表达式为

式中a、b、c为回归参数且均大于0，c＝1时为二参数数学模型。

3.2 回归结果

根据式（5）分别对表2中的全部64组试验数据及磁性物含量＞90%的52组试验数据进行曲线回归，回归结果见表4。

表4 磁铁矿磁性物含量与TFe品位的对数分布回归结果

对64组及52组数据的磁性物含量与TFe品位相关关系的回归结果进行分析，三参数对数模型的回归精度较高，表达式如下所示。

1）64组数据的磁性物含量与TFe品位数学模型（回归曲线见图4）。

2）52组数据（高品位）的磁性物含量与TFe品位的数学模型（回归曲线见图5）。

图4 磁铁矿磁性物含量与TFe品位的三参数对数分布曲线

4 结论

1）以TFe品位为横坐标，磁性物含量为纵坐标，所呈现的曲线为S型。Weibull分布可以较好的描述两者的关系。

2）以Weibull分布为基础，进行反函数变换，建立的磁性物含量与TFe品位的三参数对数数学模型，可以很好地描述磁铁矿磁性物含量与TFe品位的关系，从而通过磁性物含量的测定实现对TFe品位的快速预测。

图5 高品位磁铁矿磁性物含量与TFe品位的三参数对数分布曲线

3）鉴于SiO2含量与TFe品位之间存在显著的线性关系，通过磁性物含量计算TFe品位，进而预测SiO2含量，可以对铁精矿质量进行全面判定，实现对生产的快速指导。

4）磁性物含量的测定试验存在一定的误差影响因素，如冲洗水的流速与流量、试样的干燥判定基准、对测试结束判断依据（水清为止）的理解程度等。因此，为减小数据的离散程度，应进一步提高磁性物含量测定的准确性。

5）本文所建立的数学模型适用于太钢尖山选矿厂磁铁矿的品位计算，是一种快速检验方法，最终产品的鉴定还是要以化验结果为准。对于其他矿样，为保证计算精度应重新确定回归系数。

［1］俞中良.贵州遵义锰矿选矿产品中铁品位对锰品位的回归数学模型［J］.安徽地质，1998（4）：65－69.

［2］卢志明，张宝玉，郑秋华，等.CXG－90型磁选管的应用［J］.煤质技术，2002（5）：23－24.

［3］邓克，李维兵.铁精矿铁品位与二氧化硅含量关系的研究［J］.金属矿山，2004（3）：20－24，42.

［4］樊民强.选煤数学模型与数据处理［M］.北京：煤炭工业出版社，2005.

［5］Henk G.Merkus.Particle Size Measurements：Fundamentals，Practice，Quality［M］.Springer Science＋Business Media B.V.，Volume 17，2009.