边坡稳定性分析力学验算

刘汉秋

(贵州通力达公路工程监理咨询有限公司)

1 直线滑动面法

直线滑动面法适用于砂类土，土的抗力以内摩擦力为主，而粘聚力很小。

验算时，先通过坡脚或变坡点假设一直线滑动面，将路堤上方分割出下滑土楔体，如图1。

图1 直线滑动面法

土楔体ABD沿假设的滑动面AD滑动，其稳定系数K按下式计算(按边坡纵向单位长度计)

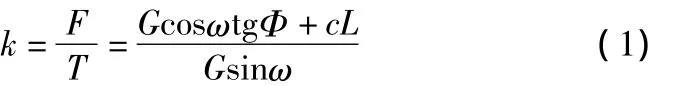
2 圆弧滑动面法

用粘性土填筑的路堤，边坡滑坍时的破裂面形状为一曲面，为简化计算，通常近似地假设为一圆弧状滑动面。分析边坡稳定性时，按其各种不同的假设，有多种方法，其中应该最广泛的是条分法(又称瑞典法)。为简化计算，还有表解法。

(1)条分法

条分法是先假定一圆弧滑动面，将圆弧滑动面以上的土体分成若干竖向土条，依次计算每个土条沿滑动面的抗滑力与下滑力，然后叠加求出整个滑动土体的稳定系数，再假定几个可能圆弧滑动面，用相同的方法求出其对应的稳定系数，最后以最小稳定系数的大小，来判别边坡的稳定性。

用条分法分析边坡稳定性时，一般假定土是均质和各向同性、滑动面通过坡脚、不考虑影响。

式中:F为沿滑动面的抗滑力，kN;T为沿滑动面的下滑力，kN;G为土楔体重量和路基顶面车辆换算土层荷载之和，kN;ω为滑动面对水平面的倾斜角，°;Ф为路堤填料的内摩擦角，°;c为路堤填料的粘聚力，kPa;L为滑动面AD的长度，m。

通过坡脚A点，再假设几个(3～4个)不同的滑动面，按公式(1)用以上的相同方法，求出相应的稳定系数K1、K2、K3……等数值，并绘出K=f(ω)曲线，用以定出最小稳定系数Kmin及对应最危险滑动面的倾角。

验算的边坡坡度是否稳定，取决于最小稳定系数Kmin的数值。当Kmin=1.0时，边坡处于极限平衡状态。由于计算的假定、计算参数(γ、ф、c)的取值都与实际情况存在一定的差异，为了保证边坡有足够的稳定性，通常以最小稳定系数Kmin≥1.25，来判别边坡的稳定性。Kmin过大，则会造成工程不经济。

当路堤填料为纯净的粗砂、中砂、砾石、碎石时，其粘聚力很小，可忽略不计，则公式(1)变为

式中:H为边坡高度，m;A、B为取决于路堤几何尺寸的系数;c为土的粘聚力，kPa;f为土的内摩擦系数，f=tgф;γ为土的容重(kN/m3);K为稳定系数。

根据计算，可制定相应的表，按表查得的A、B值代入公式(3)，即可求得相应的稳定系数，从而求得最小的稳定系数。

3 饱和土稳定性验算实例

以哈同公路土质路堑边坡试验段为例，土质为粘性土，边坡坡率为1∶1(即设计文件的设计坡率，边坡坡角为45°)。整个边坡土体处于饱和状态(相当于冰冻地区春融期在“水线”附近，被冰雪覆盖的路堑边坡冰雪融化的情况)，渗流方向基本平行于边坡。经多次跟踪观测可知，多数滑动面深度(滑动土体的厚度)在1 m左右，此处取0.8 m。经试验测得边坡饱和粘土容重γsat=20(kN/m3)，饱和土的强度参数c'=7.5(kN/m2)，φ'=10°，计算边坡稳定安全系数。

根据已知条件:

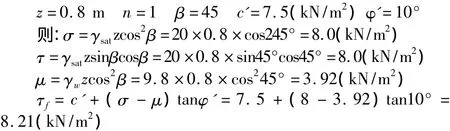
安全系数:FS=τf/τ=8.21/8.0=1.03

规范要求k值一般应≥1.25，因此该边坡处于极不稳定状态，必须采取整治措施。现假设将边坡坡率至1∶1.5(即边坡坡角为34°)，验算其稳定性:即β=34°时

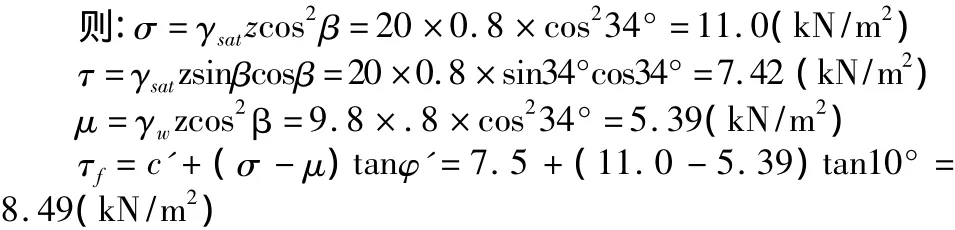
安全系数:FS=τf/τ=8.49/7.42=1.14 ＜1.25

说明该坡面仍不稳定，当植被覆盖良好，坡面土体水份易输干而饱和时极易出现滑塌，应采预防措施。

再假设将边坡坡率降至1∶1.75(即边坡坡角为30°)，再验算其稳定性，即β=30°时:

安全系数:FS=τf/τ=8.57/6.93=1.23 ＜1.25(边坡存在失稳的可能)

由此可见，即使边坡坡率放缓至1∶1.75也依然不能保证路堑边坡的稳定。由于边坡坡度的大幅度减缓，势必造成挖方量增大，占用耕地面积扩大，工程造价会明显上升，这违背我国公路建设节约耕地的实际。因此，用放缓边坡坡度的方法来保证路堑边坡稳定是不可取的，应把治理重点放在减少和排除边坡土体含水量上。