基于扩展的LBP算子地板块纹理分类研究

曹 军，王爱斐，陈 宇

(东北林业大学机电工程学院，哈尔滨 150040)

地板纹理是评定地板等级的重要标准，如何对其进行定量定性测量和分选是木材纹理识别领域的一大难题。随着计算机技术的快速发展，国内外学者将计算机视觉技术引入木材识别领域，为木材纹理识别问题提供了新思路［1-2］。

在提取纹理特征的研究方面，国内外学者进行了广泛探索，提出了许多描述纹理特征的算法，在木材纹理方面具有代表性的方法有灰度共生矩阵法、马尔可夫随机场、分形法以及小波法等，均取得了一定的成果。近年来提出一种简单、但功能强大的纹理分析方法——局部二值模式 (Local Binary Pattern，LBP)，它是一种灰度尺度不变的纹理算子，通过比较中心像素值与邻域像素值的大小得到的二进制码来反映局部纹理特征，已广泛应用于纹理分割、人脸识别等领域，但至今尚未应用于木材纹理识别。随着LBP算子日渐成熟，以及其灰度尺度鲁棒性好、计算速度快、无参量等优点［3］，该算子在木材纹理识别领域也会具有较好的发展前景。

本文提出了一种基于扩展的LBP算子地板块纹理分类方法，采用中值滤波法减少噪点对纹理特征的干扰。针对传统的LBP算子特征总量大且不能较好地区分由图像旋转得到的同类纹理图像的缺点，将均匀模式和旋转不变性与传统的LBP算子相融合，提取地板块纹理特征。最后经KNN分类器实现地板块纹理分类。实验结果表明该方法识别速度快、准确率高，实用价值大。

1 算法原理

局部二值模式 (Local Binary Pattern，LBP)最早由Ojala等人于1996年提出，是一种描述灰度范围内纹理特征的算子。LBP最初定义为:3×3窗口中，以中心像素的灰度值为阈值，周围8个像素灰度值与其比较，小于阈值标记为0，反之，标记为1。由标记值组成的8位二进制数的值即为LBP值。基本方法如图1所示。

图1 LBP基本算法实例Fig．1 LBP basic algorithm example

2002年，Ojala对LBP算子做了修改，形成以下系统理论。

在灰度图像中，定义一个半径为R(R＞0)的圆环形邻域，P(P＞0)个邻域像素点均匀分布在圆周上。设该邻域中心像素的纹理为T，则T可用该邻域中P+1个像素的函数定义［4］:

式中，g0，gM1，…gP－1为P个邻域像素的灰度值;gc为其中心像素的灰度值。若设中心像素坐标为(xc，yc)，则其邻域像素坐标 (xi，yi)为:

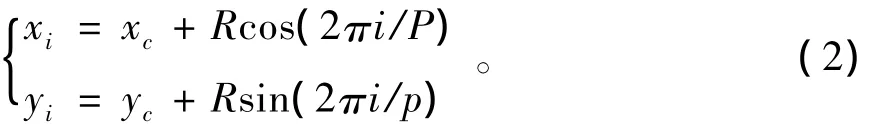
当坐标 (xi，yi)不在像素中心时，通过双线性内插法计算该位置的灰度值。如图2所示为三种不同的P，R值所对应的圆环形邻域。

图2 三种LBP模式Fig．2 Three kinds of LBP mode

与原始LBP算子相似，将邻域像素灰度值减去中心像素灰度值得到局部纹理特征T［5］:

假设差值g0，g1，…gP－1独立于gc，则上式可表示为:

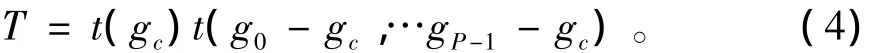
这种假设虽会导致纹理信息少量丢失，但却可以使得局部纹理描述在灰度范围内具有平移不变性［6］。又由于t(gc)代表的是图像各个像素的灰度值，与图像的局部特征无关，故可忽略不计，得到:

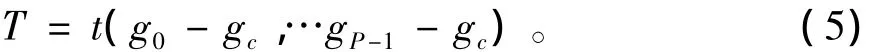
公式 (5)差值函数记录了邻域中每个像素的纹理模式，为使定义的纹理不受灰度值单调变化的影响，在此只考虑差值符号:

由此得到一个P位的二进制数，乘以相应位置权重求和得LBP值:

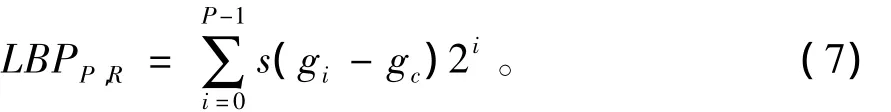
为了使旋转后图像的LBP值不发生变化，Mäenpää等人在LBP算子中加入了旋转不变性，即将圆形邻域上的点旋转得到P个LBP值，取最小值作为该邻域的LBP值［7］:

式中，ROR(x，i)是旋转函数，表示将x的二进制数按位右移i次，在此表示对P个像素点逆时针转动i(i＜P)次。

研究发现，有些模式出现的频率很低，而有一类模式可视为纹理的基本属性，它能涵盖大部分纹理模式，称之为均匀模式 (uniform pattern)。该模式下，P位二进制编码中最多有两个0到1或者1到0的变化［8］。均匀性的度量表示如下:

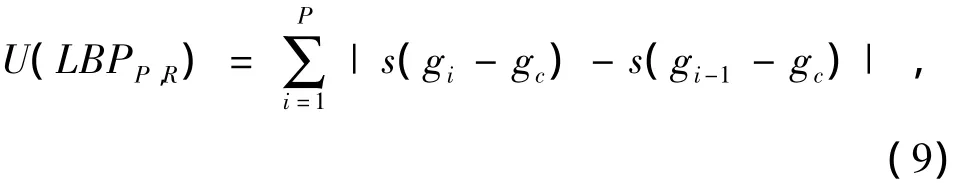
式中，gP=g0，满足U≤2的模式称为均匀模式，该模式可明显减少特征数量。将均匀模式与旋转不变性相结合，可使邻域P中的均匀模式由P×(P-1)+2个减少为P+1个，这P+1个模式称为旋转不变均匀模式，用表示［9］:

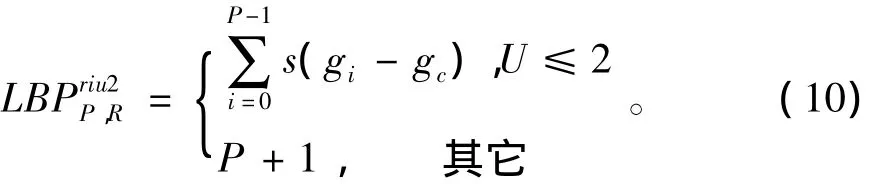
将图像旋转90度，比较旋转前后两幅图像的LBP8，1直方图和直方图。结果如图 3 所示。

图3 旋转前后图像的LBP直方图Fig．3 Image LBP histogram before and after rotation

由图3可知将均匀模式和旋转不变性与LBP算子相融合，既可大幅度地减少特征总量，为后续纹理分类减少计算量，又可保证旋转后的图像与原图像具有相同的LBP特征值。

分类器选用K最邻近节点算法 (K-Nearest Neighbor algorithm，KNN)，它是一种传统统计模式识别算法。其基本思想是在已知训练集中各样本类别的前提下，计算测试样本与训练集中各样本的距离，统计与其距离最近的K个训练样本所属的类别，将测试样本归类为K个样本中类别最多的那类，达到分类的目的。

2 仿真与实验结果

实验中选用了两种典型的地板块纹理进行分类，如图4所示。

图4 两种地板块纹理Fig．4 Two kinds of plate texture

从图4中可以看出两类地板块纹理区别明显:a类纹理走势弯曲，结构相对复杂，b类纹理走势横向，结构不复杂。实验中选取训练样本40个，其中a类样本和b类样本各20个。选取测试样本20个，a类和b类各10个。图片大小均为512×512、bmp格式。

由于LBP算子是在灰度值的基础上，通过比较邻域与中心值大小确定的最终值，因此，像素点之间不是独立存在的，一个像素值的改变会引起邻近区域LBP值也发生改变，它们之间相互影响，对噪声非常敏感。所以，在运用LBP算子提取图像纹理特征之前需对图像进行一定的滤波，以消除部分噪声的影响。在此采用传统的中值滤波方法。

滤波后运用LBP算子提取40个训练样本的纹理特征，完成训练阶段。测试阶段，同样经中值滤波和LBP提取20个测试样本的纹理特征，使用KNN分类器完成地板块纹理分类。

在运用LBP算子提取纹理特征时，需确定圆形邻域半径R和邻域像素点数P，这两个参数共同决定了提取的地板块纹理特征。实验中采用3种不同的 (P，R)组合，即 (8，1)、 (8，2)和(16，2)，分别计算扩展的LBP算子。见表1为不同 (P，R)组合的实验结果。

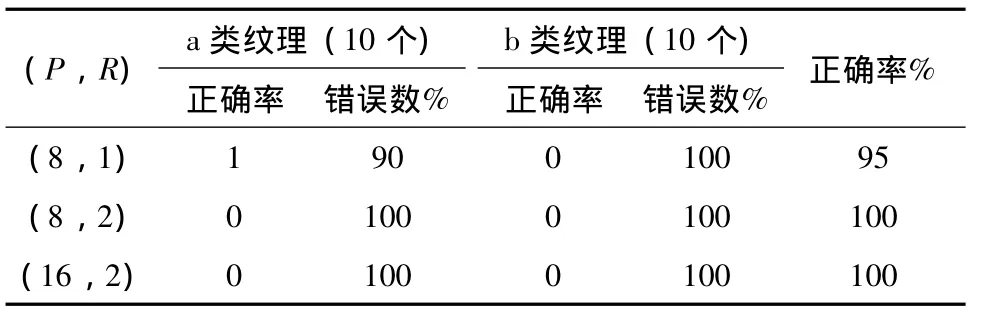
表1 不同 (P，R)组合的实验结果Tab．1 Experimental results of different(P，R)combinations

从表中可以看出 (P，R)为 (8，2)或(16，2)时识别率可达100%，但 (16，2)时计算量较大，得到的直方图维数高，导致分类时间较长。故选择 (8，2)组合。

针对上述训练样本和测试样本采用灰度共生矩阵提取 0°，45°，90°，135°的 4个方向的能量、熵、对比度以及相关性特征值，使用KNN分类器。结果见表2。

表2 LBP与GLCM分类结果Tab．2 Classification results of LBP and GLCM

表2表明LBP算子比传统的灰度共生矩阵法识别准确率高，且处理速度快，具有较高的分类能力。

3 结论

本文提出了一种基于扩展的LBP算子的地板块纹理分类方法。首先采用中值滤波去除图像噪点，减少噪点对纹理特征的干扰。提取纹理特征时，将均匀模式和旋转不变性与传统的LBP算子相融合，在保留大部分纹理特征的前提下减少了LBP特征总量，且可保证旋转后的图像与原图像具有相同的LBP特征值，经分类器后可归为同一类纹理。实验结果表明该算法适用于地板块纹理分类，分类准确率高达100%，优于传统的灰度共生矩阵法，具有很大的实用价值，也为地板块纹理分类问题提供了一种新的有效方法。

【参 考 文 献】

［1］王 晗，白雪冰，王 辉．基于空间灰度共生矩阵木材纹理分类识别的研究［J］．森林工程，2007，23(1):32-36．

［2］徐华东，王立海，倪松运．模态分析技术在木材质量检测中应用的研究进展［J］．森林工程，2007，23(6):15-17．

［3］宋本钦，李培军．加入改进LBP纹理的高分辨率遥感图像分类［J］．国土资源遥感，2010，87(4):40-44．

［4］黄金钰，张会林，闫日亮．LBP直方图与PCA的欧式距离的人脸识别［J］．计算机系统应用，2012，21(6):202-204．

［5］Shan C，Gong S，McOwan P W．Robust facial expression recognition using local binary patterns［A］．IEEE Int．Conf．on Image Processing［C］，2005:914-917．

［6］肖 霄．图像LBP特征提取的研究与应用［D］．长春:吉林大学，2011．

［7］Ojala T，Pietikäinen M，Mäenpää T．Multiresolution gray-scale and rotation invariant texture classification with Local Binary Patterns［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，2002，24(7):971-987．

［8］胡莹莹．旋转不变纹理分类算法研究［D］．天津:天津大学，2011．

［9］宋翠玉．基于扩展的局部二值模式的图像纹理及图像分类应用［D］．青岛:山东科技大学，2006．