Adaboost算法改进BP神经网络预测研究*
2013-09-05朱全银
李 翔,朱全银
(淮阴工学院计算机工程学院,江苏 淮安223003)
1 引言
反向传播BP(Back Propagation)神经网络是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一[1]。BP神经网络具有较高的预测精度、较好的通用性、较强的非线性映射能力等优点。但是,BP神经网络也存在一些缺陷,主要表现为容易陷入局部极小值、算法收敛速度较慢、隐含单元的数目选择尚无一般性指导原则、新加入的学习样本对已学完样本的学习结果影响较大等问题。
针对以上问题,提出了很多BP网络改进方法。文献[2,3]提出通过采用附加动量法和变学习率改进BP网络。附加动量法有助于使网络从误差曲面的局部极小值中跳出,但对于绝大多数实际应用问题,该方法训练速度仍然较慢。变学习率方法根据误差变化自适应调整,使权系数调整向误差减少的方向变化,但该方法仍然存在权值修正量较小的问题,导致学习率降低。文献[4,5]提出使用粒子群算法优化BP网络,使网络训练收敛到全局的最优,已解决了BP算法易陷入局部极小值的问题,但该算法只能有限提高原有BP神经网络的预测精度,并不能把预测误差较大的BP神经网络优化为能够准确预测的BP网络,且对样本数量少、样本分布不均匀而造成预测误差大的问题,优化后的网络预测能力一般得不到明显提高。文献[6]提出将Adaboost算法应用到BP网络,但选用的数据记录仅有11条,预测结果可信度不足。
本文针对上述问题,提出BP神经网络结合Adaboost算法组成的强预测器的方法,并用UCI数据库中的数据集进行仿真实验,证明本文所提方法的有效性。
2 BP神经网络与Adaboost算法
2.1 BP神经网络原理
BP神经网络是一种有监督学习多层前馈神经网络,其主要特点是信号前向传递、误差反向传播[7]。在信号前向传递过程中,输入信号从输入层进入,经过隐含层处理,到达输出层。每一层的神经元状态只影响下一层的神经元状态。判断输出层的结果是否为期望输出,如果不是,则转入反向传播,然后根据预测误差调整网络权值和阈值,从而使BP神经网络预测输出不断逼近期望输出[8]。BP神经网络的拓扑结构如图1所示。
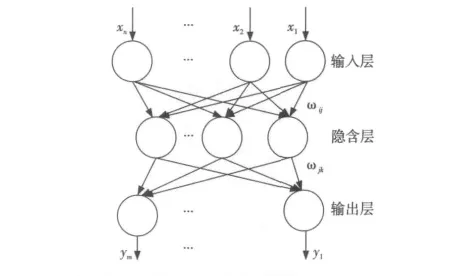
Figure 1 Topological structure of BP neural network图1 BP神经网络拓扑结构图
图1 中,x1,x2,…,xn是BP神经网络的输入值,y1,…,ym是BP神经网络的预测值,ωij和ωjk为BP神经网络权值。
2.2 Adaboost算法原理
Adaboost是一种迭代算法,通过对弱学习算法的加强而得到强学习算法,即通过一个包含关键特征的弱分类器集合,构建出具有理想分类能力的强分类器[9]。Adaboost算法的优点在于它使用加权后选取的训练数据代替随机选取的训练样本,将弱分类器联合起来,使用加权的投票机制代替平均投票机制[10]。
2.3 基于Adaboost算法的BP神经网络预测模型
本文通过对BP神经网络选取不同参数来构造多类BP弱预测器,然后使用Adaboost算法将得到的多个弱预测器组成新的强预测器。
BP神经网络在Matlab中的构造函数为:net=newff(P,T,S,TF,BTF,BLF,PF,IPF,OPF,DDF),其中,P为输入数据矩阵,T为输出数据矩阵,S为隐含层节点数,TF为节点传递函数,BTF为训练函数,BLF为网络学习函数,PF为性能分析函数,IPF为输入处理函数,OPF为输出处理函数,DDF为验证数据划分函数。一般通过设置S、TF、BTF、BLF几个参数来改变BP神经网络性能,可选择值如表1所示。

Table 1 Function parameters of BP neural network表1 BP神经网络函数参数
通过newff函数及S、TF、BTF、BLF等参数的调整,可以构造出不同类型的BP弱预测器。
本文提出的基于Adaboost算法的BP神经网络预测算法流程如图2所示。
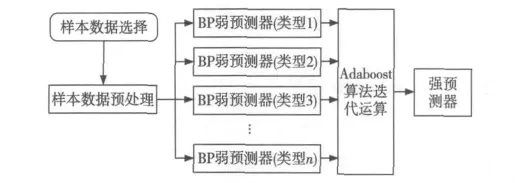
Figure 2 Prediction algorithm flowchart of BP neural network with Adaboost图2 基于Adaboost算法的BP神经网络预测算法流程图
算法详细步骤如下:
步骤1 样本数据选择及网络初始化。令迭代次数t=1时,权值分布 [)=],i=1,2,…,n,其中n为训练集样本的数量,令初始误差率εt=0。根据样本输入输出维数设计网络结构,并对BP网络权值和阈值(0<<1)进行初始化设置。
步骤2 样本数据预处理。
步骤3 BP弱预测器预测。通过选取不同BP神经网络函数构造不同类别BP弱预测器。对于t=1,…,T进行迭代,在训练第t个弱预测器时,使用BP神经网络对训练数据进行训练,建立回归模型gt(x)→y。
计算gt(x)的误差率εt:

步骤4 测试数据权重调整。令βt=,更新权重如下,式中Bt为标准化因子:

步骤5 输出强预测器函数。
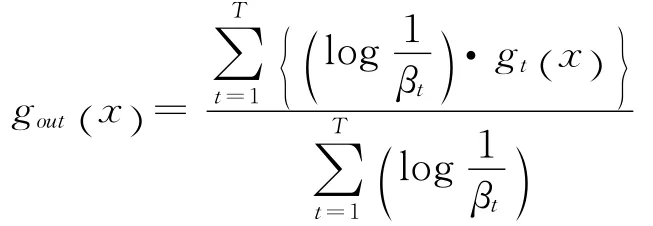
3 实验与结果分析
3.1 实验数据
UCI数据库是美国加州大学欧文分校(University of California Irvine)提供的用于机器学习的著名数据库,该库目前共有220个数据集,并且其数目还在不断增加。本实验选择UCI数据库中的 Computer Hardware、Concrete Compressive Strength两个数据集进行回归预测,数据集下载地址为http://archive.ics.uci.edu/ml/datasets/。
Computer Hardware数据集包含209条计算机CUP性能数据,该数据集共有10个属性,分别为 VendorName(P1)、Model Name(P2)、MYCT(P3)、MMIN(P4)、MMAX(P5)、CACH(P6)、CHMIN(P7)、CHMAX(P8)、PRP(Z9)、ERP(Z10),其中PRP为硬件厂商公布的性能,ERP为预测性能。从中随机选取169组数据作为训练数据,40组数据作为测试数据,选取P3~P8作为训练属性,选取Z9作为实际输出,Z10供参考。Computer Hardware数据集原始数据如表2所示。
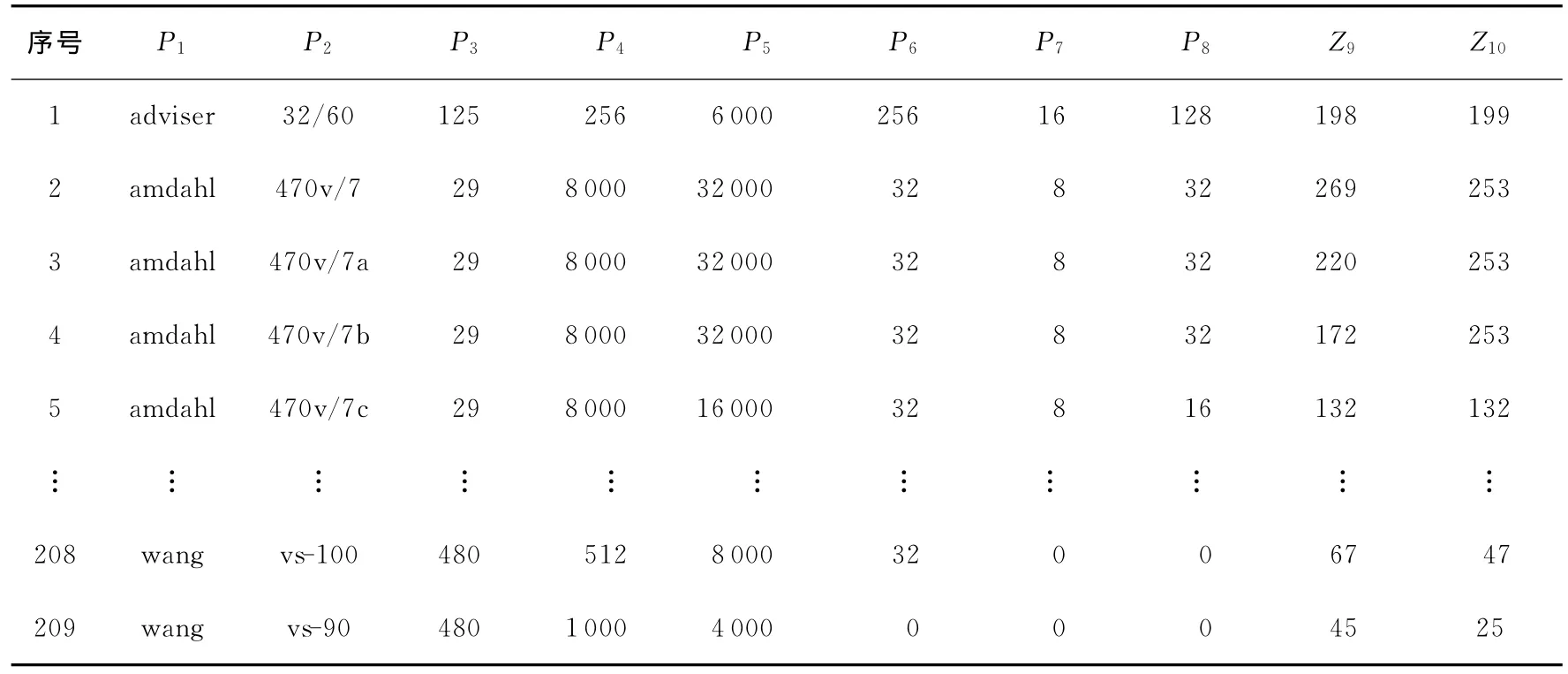
Table 2 Computer hardware dataset表2 Computer Hardware数据集
Concrete Compressive Strength数据集包含1 030条混凝土抗压强度数据,该数据集共有9个属性Cement(P1)、Blast Furnace Slag(P2)、Fly Ash(P3)、Water(P4)、Superplasticizer(P5)、Coarse Aggregate(P6)、Fine Aggregate(P7)、Age(P8)、Concrete(Z9),其中,Concrete(Z9)为输出的混凝土抗压强度。从中随机选取1000组数据作为训练数据,30组数据作为测试数据。Concrete Compressive Strength数据集原始数据如表3所示。
3.2 实验及结果分析
使用10个BP神经网络构成弱预测器序列,这10个BP神经网络的S、TF、BTF、BLF参数选择如表4所示。

Table 4 Parameter selection of BP weak predictor表4 BP弱预测器参数选择
Computer Hardware和 Concrete Compressive Strength数据集的强预测器预测误差绝对值和弱预测器预测平均误差绝对值图分别如图3和图4所示。
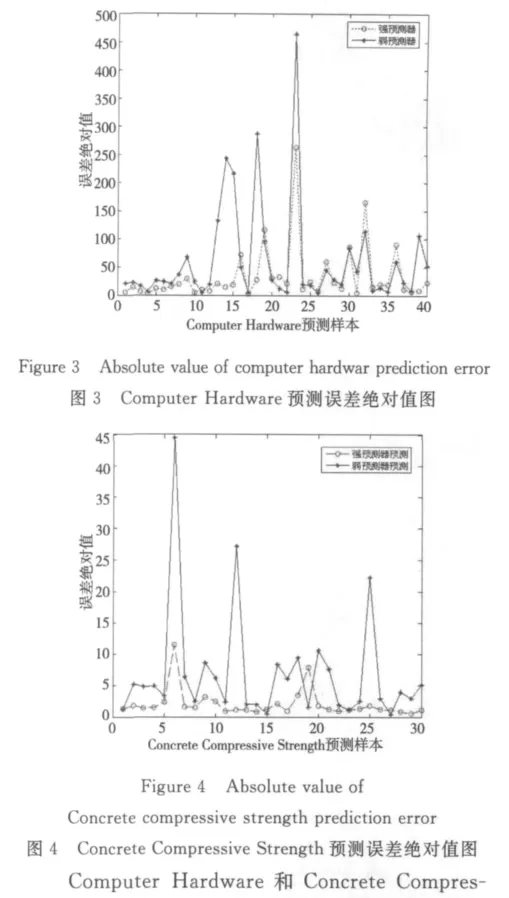
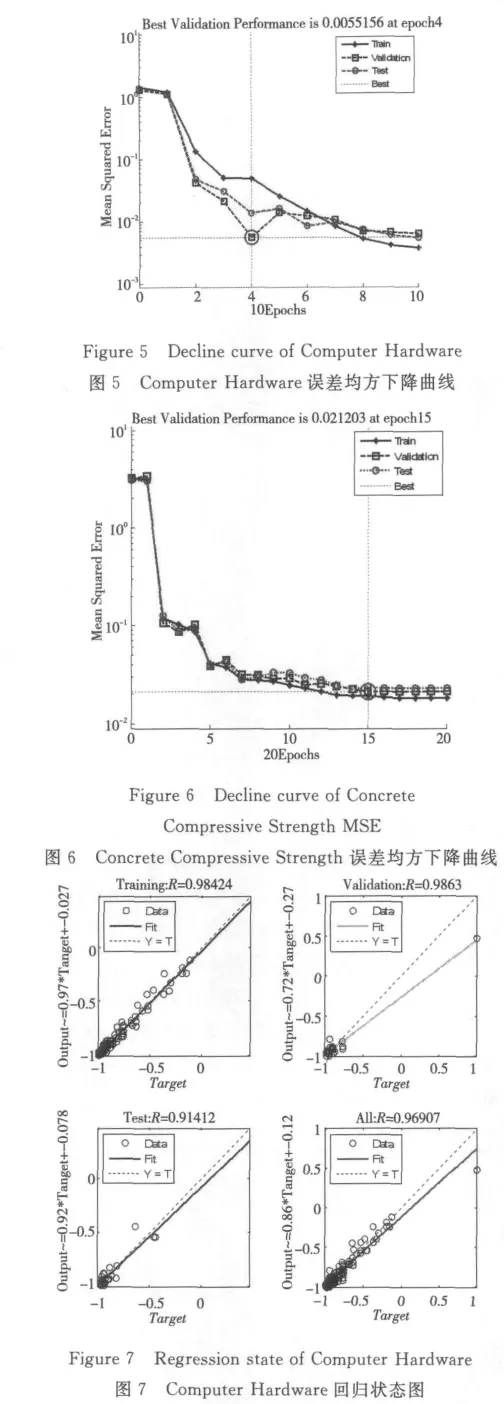
Computer Hardware和 Concrete Compressive Strength数据集的网络训练过程中误差均方下降曲线分别如图5和图6所示。
Computer Hardware 和 Concrete Compressive Strength数据集的网络训练回归状态图分别如图7和图8所示。
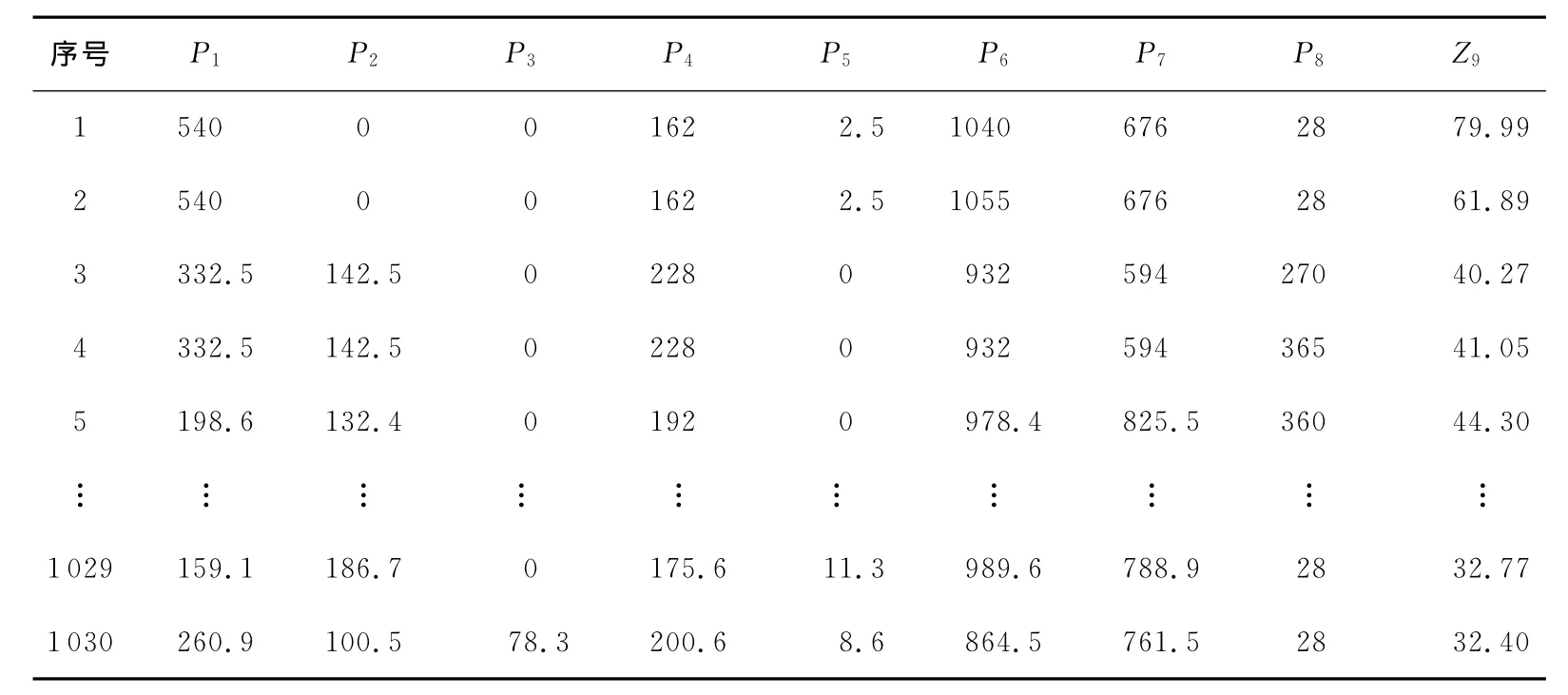
Table 3 Concrete compressive strength dataset表3 Concrete Compressive Strength数据集
Computer Hardware数据集测预误差如表5所示,Concrete Compressive Strength数据集预测误差如表6所示,预测结果平均误差绝对值对比如表7所示。
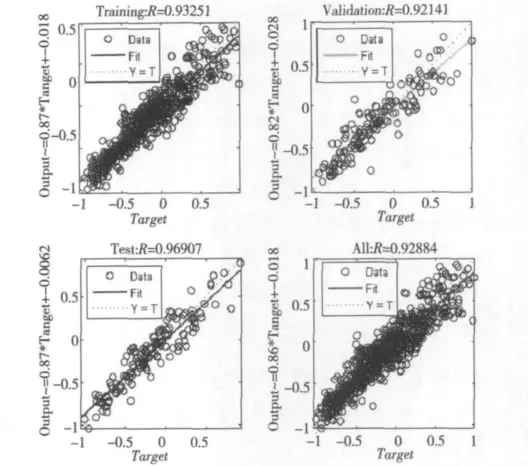
Figure 8 Regression state of Concrete Compressive Strength图8 Concrete Compressive Strength回归状态图
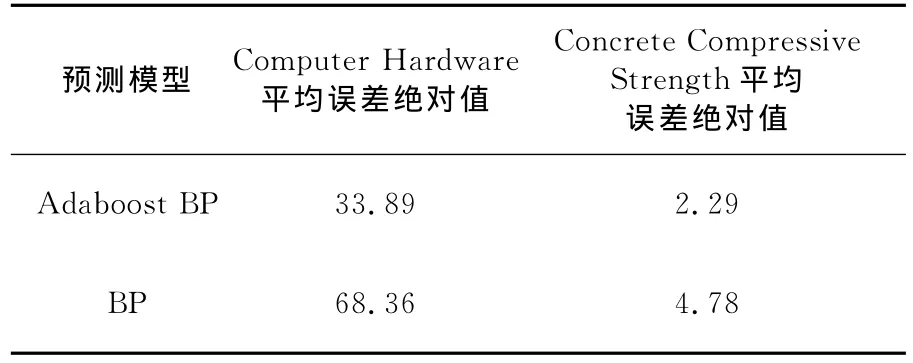
Table 7 Contrast between mean error absolute value of prediction results表7 预测结果平均误差绝对值对比
使用相关系数R来表示拟合的好坏,R的取值范围为[0 1],R越接近1,表明方程的变量对y的解释能力越强,这个模型对数据拟合得也较好。
从图3可以看出,Computer Hardware数据集预测误差值中,强预测器预测误差明显小于弱预测器预测误差,强预测器整体预测误差较小,预测结果较好。从图5可以看出,Computer Hardware数据集训练的误差均方下降曲线收敛速度较快,在第四步时达到最好的验证集效果为0.005 5,误差曲线开始趋于平缓,误差值基本不再发生变化,效果较好。从图7可以看出,强预测器预测的训练集R=0.984 2,验 证 集 R = 0.986 3,测 试 集R=0.914 1,总体R=0.969 0,回归预测结果很好。
从 图 4 可 以 看 出,Concrete Compressive Strength数据集预测误差值中,强预测器预测误差明显小于弱预测器预测误差,强预测器整体预测误差较小,预测结果较好。从图6可以看出,Concrete Compressive Strength数据集训练的误差均方下降曲线在第15步时达到最好的验证集效果为0.002 1,误差曲线开始趋于平缓,误差值基本不再发生变化,效果较好。从图8可以看出,强预测器预测的训练集R=0.932 5,验证集R=0.921 4,测试集R=0.919 4,总体R=0.928 8,回归预测结果较好。
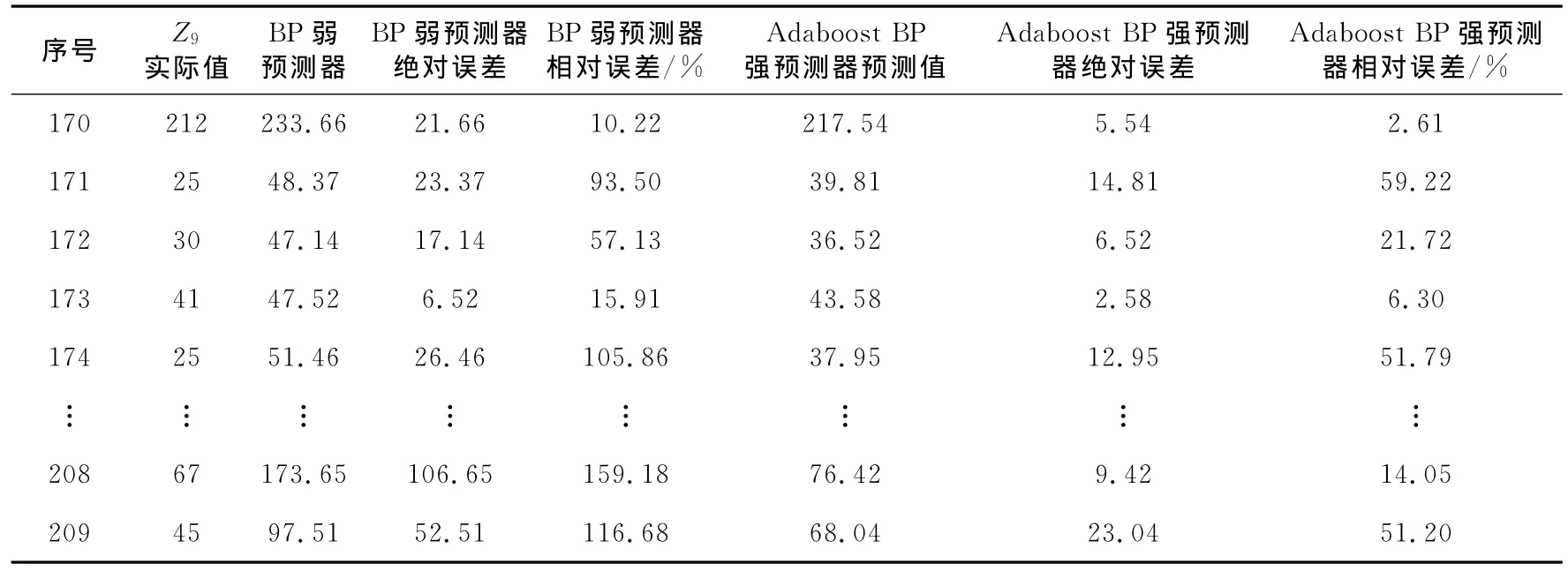
Table 5 Prediction error values of computer hardware表5 Computer Hardware数据集预测误差表
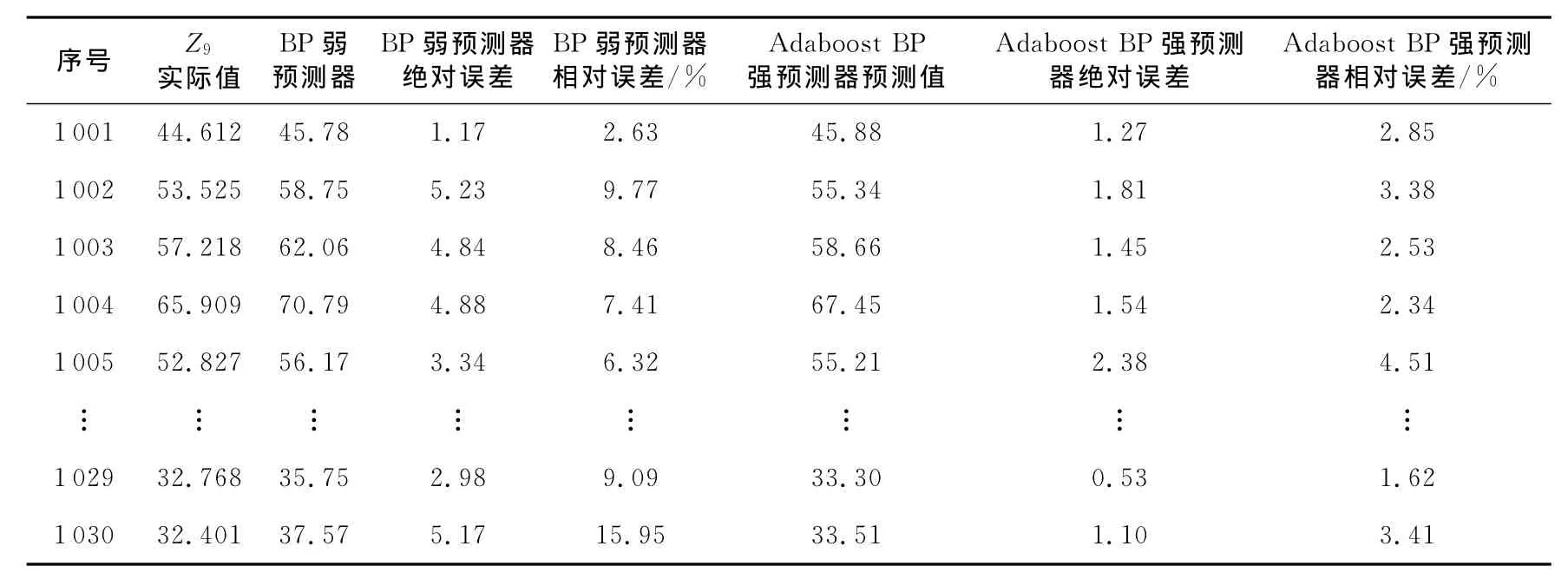
Table 6 Prediction error values of concrete compressive strength表6 Concrete Compressive Strength数据集预测误差表
从表7可以看出,基于Adaboost算法的BP强预测器在 Computer Hardware和 Concrete Compressive Strength两个数据集中的平均误差绝对值减少了近50%。
通过上述数据集的验证实验,说明本文提出的将Adaboost算法应用到BP神经网络的强预测器预测方法取得了良好的预测效果,是一种可行的改进BP神经网络预测精度的方法。
4 结束语
BP神经网络已广泛应用于分类、回归领域,取得了较好的应用效果,但仍存在易陷入局部极小值等问题。本文通过对传统BP神经网络选取不同参数构成弱预测器序列,然后结合Adaboost算构造出新的强预测器,有效降低了传统BP神经容易陷入局部极小的影响,提高了预测精度,为BP神经网络的应用提供了借鉴。
[1] Shen Xue-li,Zhang Ji-suo.Research of intrusion detection based on the BP networks and the improved PSO algorithm[J].Computer Engineering &Science,2010,32(6):34-36.(in Chinese)
[2] Li Zuo,Zhou Bu-xiang,Lin Nan.Classification of daily load characteristics curve and forecasting of short-term load based on fuzzy clustering and improved BP algorithm [J].Power System Protection and Control,2012,40(3):56-60.(in Chinese)
[3] Zhang Rui,Xu Zong-ben,Huang Guang-bin,et al.Global convergence of online BP training with dynamic learning rate[J].IEEE Transactions on Neural Networks and Learning Systems,2012,23(2):330-341.
[4] Zhang Dan,Han Sheng-ju,Li Jian,et al.BP algorithm based on improved particle swarm optimization [J].Computer Simulation,2011,28(2):147-150.(in Chinese)
[5] Bashir Z A ,Hawary M E.Applying wavelets to short-term load forecasting using PSO based neural networks[J].IEEE Transactions on Power Systems,2009,24(1):20-27.
[6] Li Song,Xie Yong-le,Wang Wen-xu.Application of adaboost_BP neural network in prediction of railway freight volumes[J].Computer Engineering and Applications,2012,48(6):233-234.(in Chinese)
[7] Lu Yu-min,Tang Da-zhen,Xu Hao.Productivity matching and quantitative prediction of coalbed methane wells based on BP neural network[J].Science China(Technological Sciences),2011,54(5):1281-1286.
[8] Shi Feng,Wang Xiao-chuan,Yu Lei,et al.30cases analysis of Matlab neural network[M].1st Edition.Beijing:Beihang University Press,2010.(in Chinese)
[9] Cheng Feng,Li De-hua.CUDA-based parallel implementation of the adaboost algorithm [J].Computer Engineering &Science,2011,33(2):119-123.(in Chinese)
[10] Pan Hu,Chen Bin,Li Quan-wen.Paper currency number recognition based on binary tree and adaboost algorithm[J].Journal of Computer Applications,2011,31(2):396-398.(in Chinese)
附中文参考文献:
[1] 沈学利,张纪锁.基于BP网络与改进的PSO算法的入侵检测研究[J].计算机工程与科学,2010,32(6):34-36.
[2] 黎祚,周步祥,林楠.基于模糊聚类与改进BP算法的日负荷特性曲线分类与短期负荷预测[J].电力系统保护与控制,2012,40(3):56-60.
[4] 张丹,韩胜菊,李建,等.基于改进粒子群算法的BP算法的研究[J].计算机仿真,2011,28(2):147-150.
[6] 李松,解永乐,王文旭.AdaBoost_BP神经网络在铁路货运量预测中的应用[J].计算机工程与应用,2012,48(6):233-234.
[8] 史峰,王小川,郁磊,等.Matlab神经网络30个案例分析[M].第1版.北京:北京航空航天大学出版社,2010.
[9] 程峰,李德华.基于CUDA的Adaboost算法并行实现[J].计算机工程与科学,2011,33(2):119-123.
[10] 潘虎,陈斌,李全文.基于二叉树和Adaboost算法的纸币号码识别[J].计算机应用,2011,31(2):396-398.
