一种基于状态反馈的位置控制算法研究

曾 辉 富春岩 李川汇 李 俊 陈春蕾

（佳木斯大学 黑龙江佳木斯 154007）

在隔震装置的性能研究中，一般采用地震模拟实验的方法，地震模拟实验台多数是通过机械振动的方式模拟地震波，目前性能比较稳定的是液压式模拟实验台[1]。实验台一般采取伺服阀（比例阀）控液压缸来实现振动模拟[2]。本文运用基于状态反馈的电液比例控制方法，通过这种控制方法，提高了振动模拟装置的系统动态性能，缩短了系统的滞后时间，减少了系统振荡和超调，增强了系统的动态稳定性。

一、控制系统的方框图

根据震动模拟装置伺服阀的力学模型和数学模型得到传递函数为[3]：

伺服比例系统的方框图如图2所示。

图2 震动模拟装置伺服比例系统方框图

二、系统的能控性和能观性

（一）控制系统的状态空间表达式

根据系统方框图得到控制系统的传递函数为：

由公式(2)得到控制系统矩阵为：

（二）系统的能观能控性

(1)将系统参数代入控制矩阵得到能控性矩阵为：

由式(5)可知，系统的能控性矩阵特性为满秩，由此可知该系统为完全能控。

(2)系统的能观测性矩阵为：

由式(6)可知，系统的能观测性矩阵特性为满秩，由此可知该系统为完全能观。

三、控制系统状态反馈及状态观测器的构造

（一）振动模拟装置控制系统的极点选取

根据控制系统方块图在MATLAB软件中建立仿真模型如图3所示。

图3 振动模拟装置MATLAB仿真模型

系统在阶跃信号输入时的响应曲线MATLAB仿真曲线如图4所示，为了进一步提高系统的性能，满足隔震模拟实验所需振动输出信号输出的要求，应用观测器和极点配置的控制方法对系统进行优化设计，图中为上升时间[4]。

图4 阶跃信号输入下的控制系统响应曲线

根据图4选取期望的极点，求得期望极点为 ：-112.379505，-112.379505，-160.5506，-160.5506。

（二）振动模拟系统状态反馈矩阵K的设计

系统的能控标准型变换矩阵如下所示：

由此可得到：

由式(9)求得 L=1048756。

（三）状态观测器的设计

分析系统的能观矩阵，因该控制系统为完全能观测，系统的完全能观测矩阵为：

将系统状态方程及输出方程转化为能观测规范型，变换矩阵T有：

则得到系统能观测规范型为：

（四）控制系统状态观测器的特征方程分析

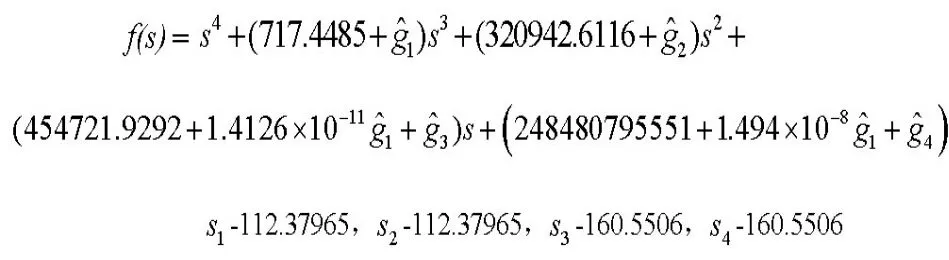
根据极点配置的要求S1-112.37965，S2-112.37965，S3-160.5506，S4-160.5506建立与之对应的特征多项式：

由于以上的两个特征多项式对应项系数相等，比较可得对应系统规范型的反馈矩阵，并得到给定控制系统状态方程的反馈矩阵G：

系统观测器方程为：

带观测器的振动模拟系统状态反馈系统方块图如图4所示。

图4 带观测器的状态反馈系统方块图

四、振动模拟控制系统仿真曲线分析

为了检验应用系统状态反馈与选取状态观测器的控制方法时的系统性能，运用工程模拟中比较常用的MATLAB仿真软件搭建仿真模型，对系统进行了仿真分析。其中图5为直接运用PID控制的系统阶跃响应仿真曲线。图6为加入状态观测器的系统阶跃响应仿真曲线。

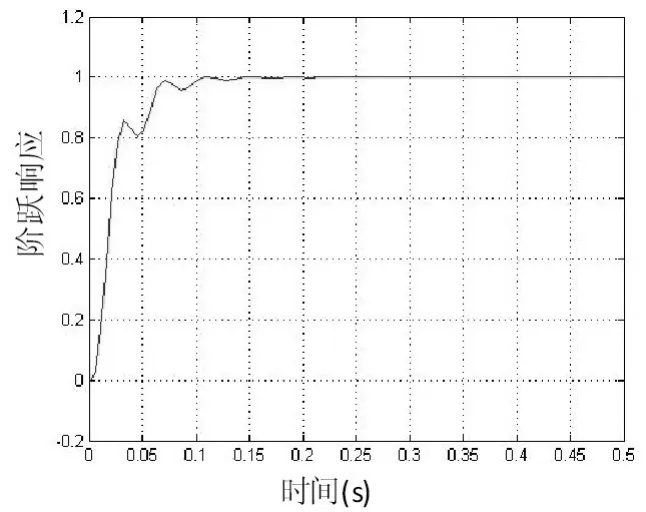
图5 PID控制的阶跃响应仿真曲线

图6 加入状态反馈的阶跃响应仿真曲线

阶跃信号的系统响应曲线表明，针对控制系统的极点，在控制系统系统中加入了状态观测器，是系统的超调量减小，响应时间缩短。控制系统能够达到隔震实验的精确控制要求。

实验表明，由于在振动模拟控制系统中加入了状态反馈的控制方法，通过极点配置，提高了振动模拟装置动态负载情况下的快速性，降低了控制系统超调，满足了振动模拟装置在高频、大强度、重载荷和动态负载等复杂工况下的系统输出稳定性要求。

[1]隋莉莉，欧进萍.MR减振驱动器用于结构振动控制的算法研究[J].应用力学学报， 2002,19(3):143-148.

[2]刘玉兰，祁桂兰.基于状态反馈极点配置随动系统的设计与实现[J].制造业自动化，2009,11(31):76-78.

[3]李书，孙忠凯，向锦武.结构控制中输出反馈鲁棒极点配置优化方法 [J].力学学报，2001,1(33):71-78.

[4]段广仁，吴广玉，黄文虎.线性系统的状态反馈特征结构配置 [J].自动化学报，1990,11(16):566-568.