离散数学命题符号化的三种方法

郭 芸，王朝晖

(苏州大学 计算机科学与技术学院，江苏 苏州 215006)

离散数学命题符号化的三种方法

郭 芸，王朝晖

(苏州大学 计算机科学与技术学院，江苏 苏州 215006)

命题符号化是离散数学课程的重要内容，看似简单，学生在学习过程中却常常犯错，甚至经典教材配套用书也存在一些错误.针对这一教学难题，分析出错的原因，并结合教学实际，提出了解决命题符号化问题的三种方法：真值表法、类比法和平衡主谓法.

离散数学；数理逻辑；命题符号化

离散数学是计算机科学中重要的基础理论之一，同时也是培养学生缜密的思维、提高学生素质的核心课程.在离散数学的教学中，解题方法起着特殊而重要的作用.通过解题方法的训练，理论联系实际，可以培养学生综合分析问题的能力.

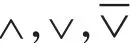
根据多年的教学发现，对具体题目的简单批改和纠正效果并不明显，因为这样做只是让学生“知其然”，未能从本质上认识错误，在遇到变化过的题目时学生还会困惑.只有从本质上剖析错误原因，找出避免错误的技巧和方法，让学生“知其所以然”，才能从根本上帮助学生杜绝错误的发生.在教学过程中总结了三种方法：真值表法、类比法和平衡主谓法.下面结合具体的例子来进行阐述.

1 真值表法

在命题符号化时，如果不能确定用哪个联结词，可以采用真值表法：首先列出所有可能的命题公式的真值表，然后比较原命题的含义与这些命题公式的真值情况，最后根据比较结果来确定联结词.

左孝凌等[1]编写的《离散数学》在国内颇具影响，许多高校将它用作本科生和研究生的教材.对于该书的第1章第3节习题(7)[1]中的命题(a)的符号化，配套的习题解答书[2]，也犯了这类错误：命题(a)为“假如上午不下雨，我去看电影，否则就在家里读书或看报.”其给出的解答是“设P：上午下雨.Q：我去看电影.R：我在家里读书.S：我在家里看报.则该命题可符号化为

另一本习题解答书[3]将该命题符号化为

而有的课件则认为应该符号化为

以上三种解答代表了的三种不同理解.为了判断究竟哪种解法正确，可以采用如下真值表法.

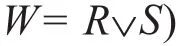
对照命题(a)的原意不难发现，当以下两种情况发生时，命题(a)为假.

1) 上午没下雨，但我没去看电影(即P=F，Q=F)；

2) 上午下雨，但我没在家里读书或看报(即P=T，W=F).

情况1)对应于表1的7、8两列，情况2)对应于表1的2、4两列，在这四列中，命题公式(1)、(3)的真值为T，命题公式(2)的真值为F，所以，命题公式(2)符合要求.

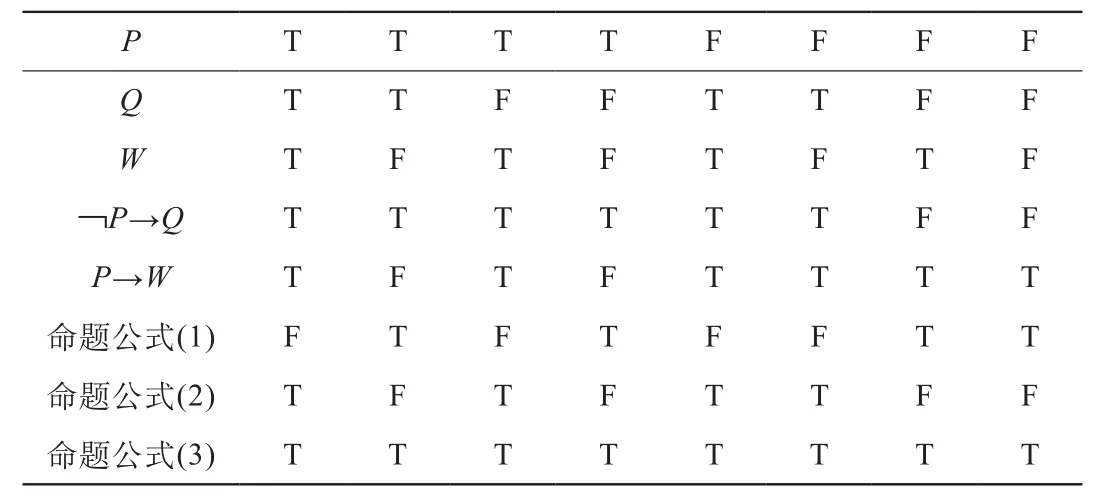
表1 真值表

2 类比法

在使用条件联结词→符号化命题时，若不确定将哪部分作为前件、哪部分作为后件，可以采用类比法：把原命题与自己熟悉的句式作比较，先“翻译”成熟悉的句式，再确定前后件.

条件命题P→Q表示“如果命题P成立，那么命题Q成立.”其中，P称为前件，Q称为后件，P是Q的充分条件，Q是P的必要条件.可以用条件命题表示的句式很多，除了“如果…，那么…”外，还有“若…，则…”，“只要…，就…”，“只有…，才…”，“因为…，所以…”，“…，仅当…”，“除非…，才…”，“除非…，否则非…”，“…，除非…”等.学生在解题过程中经常出现的主要错误是颠倒了前件和后件.

为了避免这样的错误，首先把(a)“只要P，就Q”，(b)“只有P，才Q”，作为两个典型句式重点讲解，让学生理解：在句式(a)中，P是Q的充分条件，应符号化为P→Q；在句式(b)中，P是Q的必要条件，应符号化为Q→P.然后要求学生在处理其它句式时，先将该句式“翻译”成句式(a)或(b)，再进行符号化.

例如，设P：我有空.Q：我将上街.则命题“除非我有空，我才会上街.”可以“翻译”成“只有我有空，我才会上街.”因而可以符号化为Q→P.而命题“我将上街，除非我没空.”可以“翻译”成“只要我有空，我就会上街.”，因而原命题可以符号化为P→Q.

事实上，上文提到的一些句式都能“翻译”成句式(a)或(b)，其“翻译”和符号化结果如表2所示.

3 平衡主谓法

表2 常见句式的“翻译”和符号化结果

在对命题进行符号化时，如果遇到主语是“A和B”或“A与B”等表示多人(或物)的形式时，若不确定该命题是简单命题还是复合命题，可以采用平衡主谓法.分析谓语的性质，如果谓语也是多人(或物)间的关系或者需要多人(或物)共同完成的一件事情，则该命题是一个简单命题；否则该命题就是复合命题，应被分解成多个简单命题并用联结词连接.

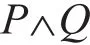
4 结论

对于数理逻辑这个学科分支来说，命题符号化是基础也是难点，初次接触的学生不容易完全掌握.以上提出的三种方法，希望能对学生有所帮助，给同仁有所借鉴.当然，命题符号化的题目形式千变万化，在教学过程中还应该注重培养学生的灵活性以及归纳和创新的能力.

[1]左孝凌，李为鑑，刘永才. 离散数学[M]. 上海：上海科学技术文献出版社，2007：1-12.

[2]左孝凌，李为鑑，刘永才. 离散数学——理论 分析 题解[M]. 上海：上海科学技术文献出版社，2005：19-64.

[3]于晶晶，张爱琴，彭程. 离散数学——全程导学及习题全解[M]. 北京：中国时代经济出版社，2007：12-15..

[4]何锋. 离散数学教学中的命题符号化难点讨论[J]. 计算机教育，2007(S)：38-40.

[5]陈敬华，胡松林. 关于命题逻辑中两个问题的思考[J]. 湖北师范学院学报：自然科学版，2011，31(4)：103-106.

[6]唐金文. 解析命题符号化[J]. 曲靖师范学院学报，2002，21(6)：71-73.

Three Skills of Proposition Symbolization in Discrete Mathematics

GUO Yun，WANG Zhao-hui

(School of Computer Science & Technology，Soochow University，Suzhou 215006，China)

Proposition symbolization，which appears to be easy but is error-prone for students，is one of the important contents of discrete mathematics.Errors even can be found in the answer books of classic teaching materials.To solve this difficult teaching problem，the cause of errors is analyzed and three skills，namely truth table method，analogism and the method of balancing subject and predicate，are put forward according to teaching practice.

discrete mathematics；mathematical logic；proposition symbolization

G642

A

1008-5475(2013)03-0044-03

2013-05-12；

2013-06-09

苏州市应用基础研究计划(SYG201116)

郭 芸(1979-)，女，江苏苏州人，讲师，硕士，主要从事应用统计和人工智能研究.

(责任编辑：沈凤英)