弯扭耦合下曲线混凝土箱梁截面应力状态的受力机理分析

何庆华，卫 星

(1.广州市高速公路有限公司，广州 510288;2.西南交通大学土木工程学院，成都 610031)

1 概述

曲线箱形梁兼具弯梁桥与箱形梁两者的特点，弯梁桥的空间受力比较复杂，没有直线形桥梁那样直观的受力特点。由于曲率的影响，曲线箱梁截面在发生竖向弯曲时，必然产生扭转，而这种扭转作用又将导致梁的挠曲变形，弯曲与扭矩互相耦联，在弯曲和扭转相互作用下，除了发生一般的弯曲和自由扭转变形外，还会发生约束扭转和箱形截面畸变［1-4］。曲线桥的变形比同样跨径直线桥大，外弧的挠度大于内弧的挠度，曲率半径越小、桥越宽，这一趋势越明显;即使在对称荷载作用下也会产生较大的扭转，通常会使外梁超载，内梁卸载;与直线桥相比，曲线梁支点反力存在外弧侧变大，内弧侧变小的倾向，内侧甚至产生负反力。

国内外研究表明，曲线梁桥的受力特性主要取决于曲率的大小，曲线梁桥的挠曲变形一般要比相同跨径的直桥大。曲线梁桥的挠曲变形一般与跨长L、曲率半径R、圆心角，以及弯扭刚度比EI/GI有关，并与荷载形式等也有关［5-11］。通常弯桥的桥面宽度与曲率半径之比越大，其与相当的直线桥的断面内力之差就越大，应力分布也越不均匀。由于扭矩的作用及截面翘曲的存在，扭转和翘曲产生的应力使得曲线梁的受力十分复杂。加大整个桥梁的抗扭刚度、增加横隔板的设置，可以改善弯桥荷载的横向分布，减小截面畸变和应力分布的不均匀。

2 曲线梁桥受力特点

主梁的弯曲程度是影响弯桥受力特性的最重要因素，曲率半径并不能全面地反映弯曲程度，能全面反映主梁弯曲程度的参数是圆心角。弯梁桥在荷载作用下的总弯矩和总剪力与同样跨径的直线梁桥相差不多，但曲梁的内扭矩比直梁要大得多。曲线梁桥中间支座支承方式将直接影响到全桥的内力分布。弯-扭耦合作用是曲线梁重要受力特点。

圆弧梁的坐标系及外力如图1所示，坐标轴x指向圆心，y轴向下，z轴指向弧线切线前进方向。ξ是沿x方向位移，η是沿y方向位移，ζ是z方向位移，θ是绕x轴的转角。qx、qy、qz是作用在梁上的分布力，mx、my、mz是作用在梁上的分布力矩。

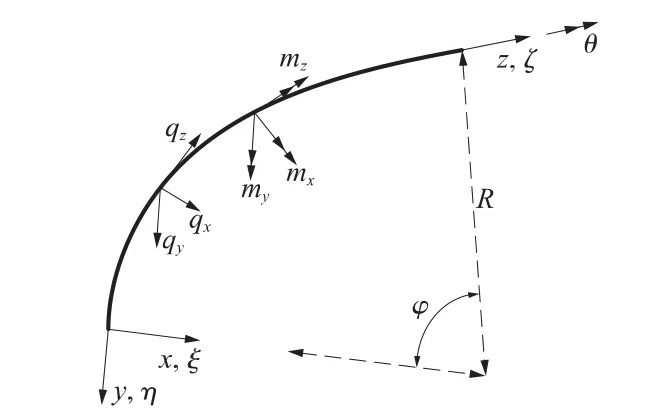
图1 圆弧梁的坐标系位移和外力

曲梁每个截面有6个内力分量:轴力N，x和y方向剪力Qx和Qy，扭矩Mz，面内弯矩Mx，面外弯矩My。取出一圆弧微段，可以建立其6个平衡方程。这6个方程中可以消去N，Qx和Qy，得到只含有弯矩、扭矩的3个平衡方程

第1个方程是面外弯矩平衡方程，此方程中内力项只含有My，所以圆弧梁单元的面外弯矩是独立的。第2个和第3个方程是面内挠曲和扭转两个方向的平衡方程，两个方程都含有内力项Mx和Mz，可见曲线梁的扭矩和面内弯矩是耦合在一起的。实际上这一效应是由于沿着弧线坐标前进，坐标系会发生绕竖直轴的转动，致使终点的Mx在起点的z方向上有分量，终点截面的Mz在起点的x方向上也有分量，而y轴指向不变。这就是曲线梁弯矩和扭矩相耦合的来源。

通过曲梁变形分析，可以得出圆弧梁截面轴向应变、面内曲率、面外曲率以及绕z轴的扭转率与梁的位移直接的关系，这样得到4个几何方程［11］。

根据应力-应变关系，对应力在截面上进行积分，可以得到轴力N，两个方向的弯矩以及扭矩与截面应变的关系。再将上述几何方程代入，就得到了截面内力与截面变形的方程式。这一关系式代入上述方程(1)，就得到只含梁位移的3个微分方程

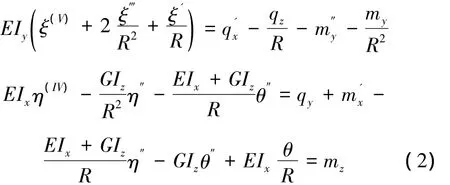
上述方程推导中略去了翘曲扭矩。从方程(2)第1式可见，曲梁的横向位移是独立的。从第2和第3个方程看，挠度和扭转位移是耦合在一起的，这是面内弯矩和扭矩相耦合的自然结果。

由于曲线梁桥存在弯扭耦合作用，其受力特性与直梁桥截然不同。梁的弯曲自然使得荷载偏离梁两端支座连线，这自然引起梁的扭转(扭矩)，扭矩使得曲线外侧腹板的剪力增大。同时，由于平面曲线存在，会产生较大的横向弯矩。横向弯矩引起腹板外侧正应力增大。曲线梁中预应力和横向分量会使得曲线内侧腹板受拉，外侧受压。因此，曲线梁桥受力分析应主要关注由扭矩和横向弯矩引起的截面受力变化影响因素及其趋势。

3 曲线梁内力分析

曲线箱梁中，扭转效应即截面扭转和畸变引起的纵、横截面上的应力，比同样条件的直线箱梁大很多，弯扭耦合作用明显，扭矩往往成为控制设计的关键因素之一，而翘曲应力与基本弯曲应力和扭转剪应力相比，所占比例比较小，一般都在10%以下，在初步设计时可以不予考虑，但施工设计时需予以计算。

选取一单箱形截面、60 m单跨简支梁，刚性桥墩，曲线半径60 m。利用TDV有限元分析软件，选用板单元建立空间有限元模型，如图2所示。计算得到自重下截面应力分布，通过对截面应力进行积分得到截面内力［12］。

图2 桥例壳单元模型

曲线梁对截面竖向轴向不对称，左右半侧箱梁的顶、底板存在分布弯矩和竖向剪力，因此左右侧半截面的受力不相同。计算结果表明，内外侧半截面的弯矩分布图形有较大差别，外侧半截面的跨中弯矩小于内侧半截面;内侧半截面在支座处出现了较小的负弯矩区段，这是内侧支座的负反力所致，如图3所示。曲线梁全截面剪力分布与直线梁相同，但内外侧半截面剪力分配差别就很大了，特别是在支座附近区段，内侧半截面剪力与直线梁剪力方向相反，如图4所示。

图3 弯矩分布

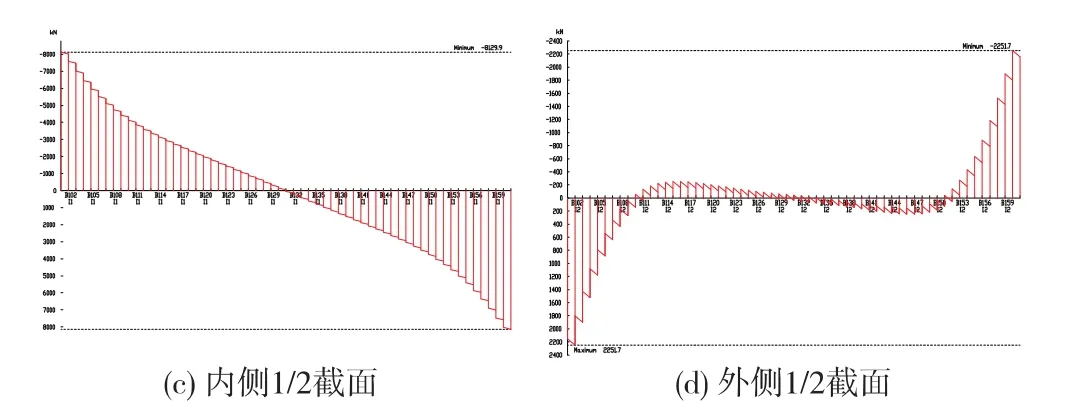
图4 剪力分布

4 曲线梁截面应力分布

4.1 正应力分布

图5给出了自重作用下3种不同曲线半径(60，180 m和300 m)曲线梁桥顶板正应力沿横向分布趋势。为便于比较，图6给出了等跨径的直桥顶板正应力分布。可以看出，直线桥和曲线桥顶板正应力分布差别较大，曲线梁桥顶板正应力除在曲线外侧腹板处出现极大值外，曲线内侧顶板正应力在截面边缘逐渐增大。

图5 曲线梁桥顶板正应力分布

曲线梁桥正应力分布在曲线外侧小，曲线内侧大这一现象是由于曲线内外侧桥梁弧线长度差异引起的，如图7所示。

图6 直线桥顶板正应力分布

图7 弯桥曲线半径示意

假设:(1)同一截面各位置处竖向挠度与梁心挠度差别不大，均取截面形心处的挠度，即

(2)截面面内弯曲变形是绕过曲线圆心的水平中心轴转动实现的。图7中微梁段梁端相对转角(绕径向)是

在(x，y，z)坐标处的轴向位移量为:ζ(x，y，z)=κ(z)y

在(x，y，z)坐标处的应变为

该式与直线桥的差别在于:求应变时直线桥未变形纤维长度为Rdφ，曲线梁桥横向x处未变形纤维长度为(R-x)dφ。把应变式子中的系数1/(R-x)取幂级数第一项近似，得

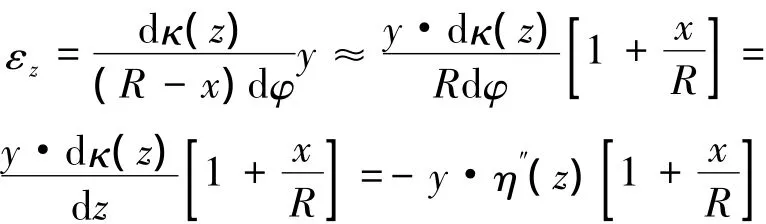
当x=0时，就退化为直线桥的应变计算式

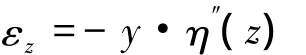
可见曲线梁桥横向x位置处的正应力要在按直线梁桥计算的应力基础上乘以一系数［1+x/R］;其中x以向曲线内侧为正。因此，曲线梁桥顶底板正应力均是曲线内侧大，曲线外侧小。从上式也可看出，随曲线半径的减小，这一变化趋势加剧。

不考虑剪力滞效应，按照上式计算顶板应力横向分布图式如图8所示。对比图8与图5，可知曲线内侧正应力增大的主要原因就在于曲线内外侧弧长不同引起的。在图8应力分布基础上叠加剪力滞效应后就得到图5应力分布。

图8 弯桥顶板正应力分布

综上所述，考虑曲线梁桥顶底板正应力不均匀分布时应计入两个因素:(1)由于内外侧弧长不等引起的应力增大系数［1+b0/R］，其中b0为顶板或底板半宽;(2)剪力滞系数，曲线桥梁可以取与直线梁桥相同的剪力滞系数。

两种因素出现最大值的位置不同，不宜直接叠加，建议按如下考虑:(1)先按［1+x/R］算出腹板处和桥宽最外侧的应力增大系数αw，αf;(2)腹板处再考虑剪力滞后系数 λ，得腹板处应力增大系数 λαw;(3)取max(λαw，αf)为总的应力增大系数。本算例桥梁曲线半径为60 m和180 m时，系数αf＞λαw，曲线半径为300 m 时，λαw＞αf。

4.2 剪应力分布

截面竖向剪应力按两种方法计算:(1)壳单元计算的应力结果在全截面上积分，得到全截面上的剪力和扭矩，再按照梁单元理论，用积分得到的截面剪力和扭矩计算此点应力;(2)用单个壳单元面积积分内力除以积分面积的平均值。

桥例外、内侧腹板剪应力(梁高度中心)见图9和图10。

图9 曲线外侧腹板竖向剪应力

为便于比较，计算了同跨径直线桥腹板同一位置剪应力，剪应力沿跨分布如图11。直线桥用壳单元与梁单元算得的剪应力差别不大，只是在支座位置处由于竖向力局部效应，略有差别。而曲线梁腹板剪应力的壳单元结果与梁单元结果差别较大。

曲线桥腹板竖向剪应力分布如图12所示，外侧最大值3.56 MPa，内侧最大值1.8 MPa。

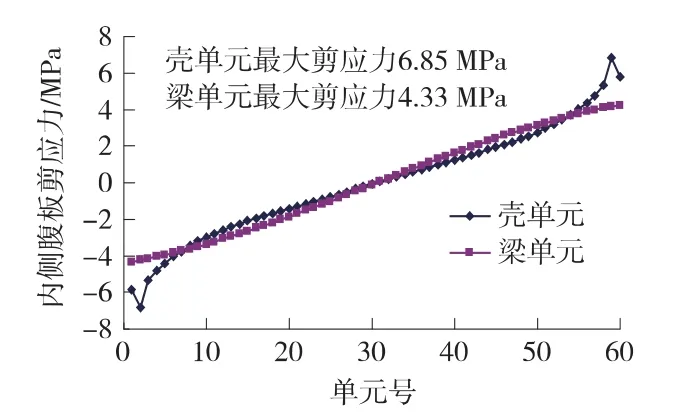
图10 曲线内侧腹板竖向剪应力

图11 直桥腹板剪应力

图12 曲线桥腹板竖向剪应力分布(单位:MPa)

直线桥自重下腹板剪应力分布如图13所示，最大值2.5 MPa，方向向上。比较曲线梁和直线梁腹板剪应力，可知曲线梁外侧腹板剪应力由于扭矩作用而显著增大，内侧腹板剪应力减小。扭矩作用对腹板剪应力分布影响很大。

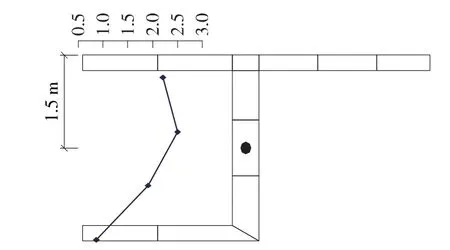
图13 直桥腹板剪应力分布(单位:MPa)

自重作用下顶底板剪应力分布如图14所示，剪应力朝向箭头方向。截面剪力方向向上，扭矩为正(指向截面外)。

通过对曲线梁截面应力分布状态分析，可以得出以下结论。

图14 曲线梁顶底板外缘剪应力分布(单位:MPa)

(1)曲线梁内外侧半截面的弯矩存在差异。外侧半截面的跨中弯矩小于内侧半截面，这是由于曲线内侧跨度小、刚度大，因此分配到的内力大所致。内侧半截面在支座处出现了较小的负弯矩区段，这是内侧支座的负反力所致。

(2)曲线梁内外侧半截面的剪力存在差异。特别是在支座附近区段，内侧半截面剪力与直线梁剪力方向相反。

(3)考虑曲线梁桥顶底板正应力不均匀分布时应计入由于内外侧弧长不等引起的应力增大系数及剪力滞系数。

(4)比较曲线梁和直线梁腹板剪应力，曲线梁外侧腹板剪应力由于扭矩作用而显著增大，内侧腹板剪应力减小。

［1］姚玲森.曲线梁［M］.北京:人民交通出版社，1992.

［2］邵容光，等.混凝土弯梁桥［M］.北京:人民交通出版社，1996.

［3］李惠生，张罗溪.曲线桥结构分析［M］.中国铁道出版社，1992.

［4］高岛春生.曲线梁桥［M］.张德礼，译.北京:中国建筑工业出版社，1979.

［5］Sennah，K.M.， Kennedy， J.B.State-of-the-Art in Curved Box-Girder Bridges［J］.Journal of Bridge Engineering，2001，6(3):159-167.

［6］Sennah，K.M.，Kennedy，J.B.Literature Review in Analysis of Curved Box-Girder Bridges［J］.Journal of Bridge Engineering，2002，7(2):134-143.

［7］Cordtz，K.Design of Curved Post-Tensioned Bridges for Lateral Prestress Forces［M］.David Evans and Associates，Inc.，Roseville，California，2004.

［8］Ibrahim，A.M.M.，et al.Torsional Analysis and Design of Curved Bridges with Single Columns-LFD vs.LRFD Approach［C］//Paper presented at the Western Bridge Engineers Conference.Portland，OR.:2005.

［9］徐艳秋，许克宾，王丽.薄壁梁桥空间有限元分析［J］.土木工程学报，2003，36(2):58-62.

［10］吴卫祥，预应力混凝土曲线梁桥的受力分析［D］.长沙:湖南大学，2005.

［11］孙光华.曲线梁桥计算［M］.北京:人民交通出版社，1997.

［12］西南交通大学.连续曲线梁桥施工及运营安全控制技术研究报告［R］.成都:西南交通大学，2011.