基于Abaqus的汽车车门瞬态应力分析

邓雄志 王 力 申 苗

（广州汽车集团股份有限公司汽车工程研究院）

1 前言

在实际使用过程中，乘用车的车门开闭是使用频次非常高的行为，因而设计时必须保证车门在使用过程中经多次开闭后状态良好，如钣金无开裂、锁机构锁止正常、下垂量不会导致车门干涉等[1]。目前，车门开闭性能主要根据车门开闭耐久试验来评估，但耐久试验耗时长、成本高，所以车门的开闭仿真模拟成为车门开发过程中的主要设计手段[2]。

车门的开闭仿真是一个强非线性 （材料非线性、几何非线性和边界非线性）的动力学问题，因而较难准确模拟车门的开闭行为并获得精确的数值解[2]。为此，本文提出了一种新型刚柔体混合的锁机构模型以及胶条接触压强的定义方法，并根据模态试验拟合系统的阻尼系数，利用有限元分析软件Abaqus建立了某A级轿车的车门模型和刚柔体混合的锁机构模型，进行了车门关闭的冲击应力分析，通过与试验结果对比研究，验证了该分析方法的精确性。

2 有阻尼的多自由度系统动力学方程

车门的关闭实质是一个有阻尼多自由度系统的动力学问题。任何实际的机械系统都存在阻尼因素，如材料的结构阻尼、介质的粘性阻尼等，各种阻尼的性质和数学描述不一，工程上为了简化计算和分析过程，通常将各种非粘性阻尼简化为等效粘性阻尼，等效的原则是使非粘性阻尼在一个周期内耗散的能量与等效粘性阻尼在同一周期内耗散的能量相等[3]。为考虑车门的振动衰减，利用Abaqus进行动力学计算时设置了阻尼参数。下面推导出有阻尼多自由度系统的动力学方程及其解法。

假定阻尼力为广义速度的线性函数，则阻尼力方程为:

式中，Ddi为阻尼力；cij为阻尼影响系数；qj为广义坐标。

考虑Ddi的作用，拉格朗日动力学方程为:

为简化计算，设系统沿各广义坐标均受到相同的频率和相位广义简谐力的激励，令 Qi=Fi0eiωt，qj用xj表示，将式（2）写成矩阵形式，则得到多自由度阻尼系统的振动方程为:

式中，M、C和K分别为质量、阻尼和刚度矩阵；x为坐标列阵；F0为广义激励力列阵。

将式（3）进行式（4）的坐标变换到主坐标 xp，再令等式两侧左乘ΦT（转置矩阵），代入式（5），可导出用主坐标描述的动力学方程式（6）。

式中，Φ 为模态矩阵；xp为主坐标列阵；Mp、Cp和Kp分别为主质量矩阵、模态阻尼矩阵和主刚度矩阵。

假定阻尼矩阵C与质量矩阵M和刚度矩阵K有式（7）的比例关系，则式（6）可解耦成n个主坐标微分方程，如式（8）。

式中，ζj为第j阶模态的阻尼比。

由式（9）可知，多自由度有阻尼系统的自由振动或受迫振动的分析方法与单自由度有阻尼系统完全相同，多自由度有阻尼系统的动力学方程可解耦成n个主坐标微分方程[3]，通过解微分方程即可得到方程的根。

3 瞬态应力分析

3.1 分析模型

汽车车门的关闭经过了车门绕铰链轴自由旋转、接近关闭位置时的胶条接触、缓冲块接触、门锁系统锁止等一系列过程。这些过程中，车身近似没有位移，因而用刚体模拟车身侧围。车门模型包含车门钣金、门锁系统、玻璃和玻璃升降器、门把手、扬声器及内饰板。其中门把手、扬声器、内饰板用集中质量模拟，用分布耦合单元与车门钣金相连[4]。以某A级汽车的前门为例在Abaqus中建立分析模型，如图1所示。

门锁系统采用刚体和柔体混合建模，门锁壳体用刚体模拟，锁销、锁扣、橡胶块用实体单元模拟，扭转弹簧等弹性元件用连接（connector）单元模拟，门锁机构有限元模型如图2所示。该锁机构模型更真实地模拟了门锁的锁止行为，使车门动能到内能的转化更平稳，同时克服了传统连接单元瞬间锁止导致局部瞬态应力过大的问题，并且无需定义锁止点。

车门上的缓冲块用实体单元模拟。胶条最理想的模拟方式是用较细的网格建立胶条的实体模型，用超弹性材料模拟，但这种模拟方式需要重新对胶条的材料参数进行大量标定，而且超弹性材料在显示动力学中收敛性和稳定性均较差，较细的胶条网格和阻尼会增加模型的计算时间，因而采取一种更实用的方式模拟，即通过定义接触对的接触属性模拟胶条。由于车门有2道胶条密封，且不同断面处胶条的接触压力和接触面积有差异，要完全模拟胶条的行为比较困难，为此将2道胶条密封简化为1道胶条，胶条的缓冲阻力采用统一的接触属性定义。接触属性由单位长度胶条的位移-压力曲线转换而来，用于接触属性定义的某胶条的位移-压力测试曲线如图3所示。

从获得的胶条位移-压力测试曲线中选择若干点，然后将压缩位移d转换成接触面之间的距离D，胶条的原始厚度H（常数）等于d与D之和；压力转换为压强P0，P0等于压力除以受压面积，此处受压面积为100 mm×20 mm。由于2道胶条用1道胶条模拟，最后压强数值P定义为P0的2倍。胶条接触属性如表1所列。

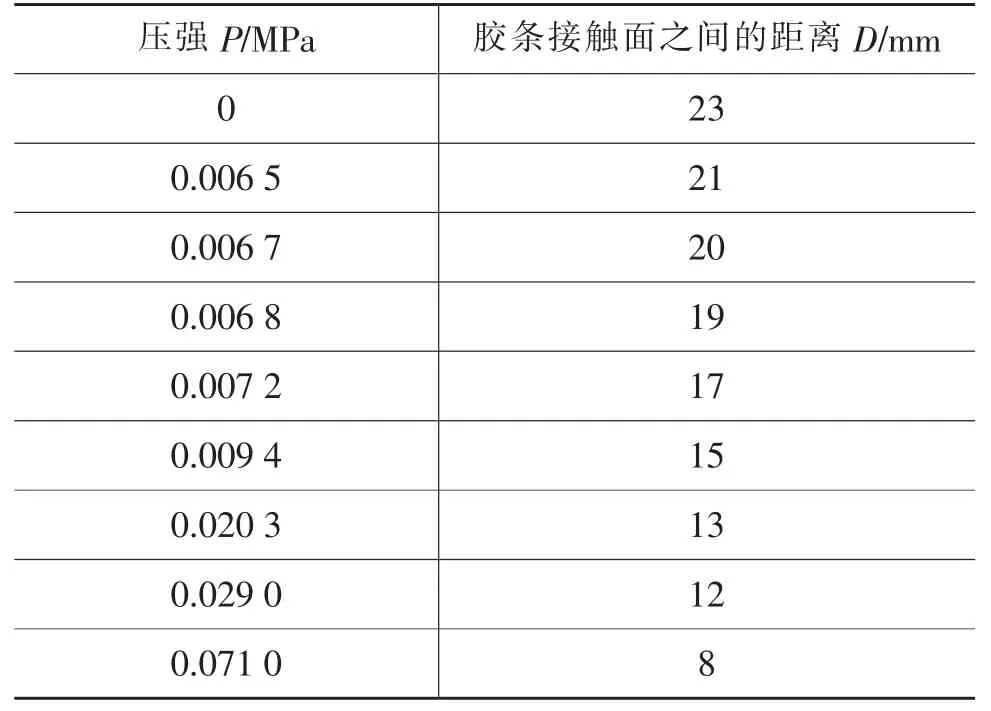
表1 胶条接触属性

3.2 模态分析及阻尼定义

车门系统的阻尼构成因素较多且性质复杂，工程上一般采用等效粘性阻尼近似模拟[8]。此处采用瑞利阻尼模拟等效粘性阻尼，瑞利阻尼是Abaqus中应用最广泛的阻尼[5]。Abaqus/explicit算法中的瑞利阻尼表达式为:

式中，ξi为第 i阶模态阻尼比；a、b 为系数；ωi为第 i阶模态的角频率[6]。

工程应用时一般通过试验测试前2阶的角频率及阻尼比，然后由式（11）～式（15）求出系数 a、b。

本文通过模态分析确定车门的前2阶固有频率。进行车门模态分析时，有限元模型应包含车门钣金、门锁系统、玻璃和玻璃升降器、门把手、扬声器以及内饰板等附件系统。图4为车门前2阶模态云图。

在Abaqus/explicit算法中，b值为与刚度成比例的阻尼系数。定义b值会显著减小模型的稳定时间增量步，导致模型计算代价太大；动态事件又不宜采取过大的质量缩放，且b值只对高频的影响显著，低阶情况下并不会对实际阻尼比有显著影响，因而本文仅定义阻尼系数a。此处取a=4，代入式（11）得前2阶阻尼比分别为0.80%和0.75%，试验测得前2阶阻尼比分别为0.74%和1.08%，由此可知，定义a=4与试验吻合较好。

3.3 结构应力分析

合理定义结构阻尼有助于结构能量合理耗散，进而可获得较精确的仿真结果。在Abaqus中进行车门开关应力分析时，只需要分析车门即将关闭瞬间到车门锁扣锁死的这段时间即可，因为这段时间几乎包含了车门内板应力历程最大的几个应力循环[8]。进行应力分析时，约束侧围，车门开启5°，给车门施加重力场和初始角速度，使车门锁扣处初速度为1.3 m/s，车门以该初速度绕铰链轴旋转，通过胶条和缓冲块的接触减速缓冲，直到锁机构锁止，如图5所示。

车门在闭合过程中同时受到空气阻力作用，但由于空气阻力与整车的密封性、车门开闭速度、车内空间、车门面积等因素有较大关系，属于耦合问题，而此问题在有限元工程应用中尚不成熟；另外，不考虑空气阻力属于偏于保守的工程计算，仍然具有指导意义。因此，本文未考虑空气阻力影响。

结构应力分析完成后，需要检查锁机构的锁止状态、能量平衡状态及伪应变占内能的比值[9]，工程应用中一般要求总能量变化不超过5%，伪应变能与内能的比值小于10%。模型能量变化如图6所示。

在仿真时长为0.12 s的计算过程中，车门内板上的锁安装孔附近、玻璃升降器前导轨下安装孔、下缓冲块安装孔、上缓冲块安装孔等区域分别在0.068 s、0.076 s、0.078 s 和 0.080 s 时出现应力峰值，应力大小分别为 162 MPa、161 MPa、163 MPa 和163 MPa，车门内板应力云图如图7所示，应力历程如图8所示。

车门内板所用钣金材料屈服极限为165 MPa。由上述可知，在门锁安装孔附近、缓冲块安装孔和玻璃升降器前导轨下安装孔附近应力较大。车门关闭过程中门锁和锁扣碰撞后即锁死，同时有间隙可允许锁扣和锁销有少量游动，因而门锁安装孔处在碰撞时出现一次较大的应力峰值，而后迅速衰减，锁扣和锁销游动时会使局部保持较低的应力震荡。同样，缓冲块安装孔在第1次碰撞时出现应力峰值，之后衰减到较低水平。玻璃升降器前导轨下安装孔处由于导轨和电机等附加质量的惯性力影响，计算时间内的几个应力循环的应力幅值较高[10]。经分析可判断玻璃升降器前导轨下安装孔可能最先出现破裂，该结论在车门开闭耐久台架试验中得到验证，如图9所示，即该车门在经过6万次的开闭耐久性试验后，玻璃升降器前导轨下安装孔破裂，需要设计变更。

4 结束语

通过对车门结构的建模和仿真参数的合理定义，准确模拟了车门关闭过程中的瞬态响应，获得了较精确的应力结果，预测了车门关闭冲击的应力分布，为车门的强度耐久设计提供了良好依据。同时利用该应力结果做车门的开闭耐久分析，得到玻璃升降器前导轨下安装孔寿命为4万次，进一步验证了瞬态应力分析的准确性。本文所用方法也适用于发动机罩、行李箱盖的关闭冲击应力分析。

1 黄金陵.汽车车身设计.北京:机械工业出版社，2007.

2 叶青，洪光辉，王得天，等.惯性释放在汽车飞翼门slam分析中的应用.计算机辅助工程.2011，20（2）:136～142.

3 刘延柱，陈文良，陈立群.振动力学.北京:高等教育出版社，1998.

4 解跃青，雷雨成.车门有限元分析中工况的确定及数值分析结果评价.机械设计与制造，2002（5）:62～63.

5 Stoker J J.Nonlinear vibrations in mechanical and electrical systems.New York:John Wiley&Sons.INC， 1992.

6 庄茁，张帆，等.ABAQUS非线性有限元分析与实例.北京:科学出版社，2005.

7 Phan A V，Gray L J，Salvadori A.Transient analysis of the dynamic stress intensity factors using SGBEM for frequency-domain elastodynamics.Computer Methods in Applied Mechanics and Engineering.2010， 199 （45/48）:3039～3050.

8 Lijuan Liao，Toshiyuki Sawa.Finite element stress analysis and strength evaluation of epoxy-steel cylinders subjected to impact push-off loads.International Journal of Adhesion&Adhesives.2011， 31（5）:322～330.

9 顾克秋，张鸽.高炮炮箱瞬态弹塑性有限元分析.南京理工大学学报，2001， 25（6）:566～569.

10 Yim S C S，Lin H.Chaotic behavior and stability of freestanding offshore equipment.Ocean Engineering.1991，18（3）:225～250.