混合动力汽车传动系统共振转速优化分析
2013-09-04于海生张建武
王 凯 于海生, 邹 良 张建武 张 彤
(1.上海交通大学;2.上海华普汽车有限公司)
1 前言
随着汽车工业的发展,人们对汽车各项性能要求越来越高,乘坐舒适性作为一项直接反映乘客感受的指标,其重要性不言而喻,因此需要对汽车振动和噪声进行有效控制。造成汽车振动和噪声的因素很多,其中动力传动系统的扭转振动是引起汽车振动和噪声的主要原因之一[1]。
混合动力汽车的关键技术之一是多能源的耦合问题[2],因此混合动力汽车的核心部件——动力复合装置一直是各研究机构和厂商的研发重点。行星齿轮传动因具有普通定轴齿轮无法比拟的输入输出的同轴性、良好的功率分流(汇流)、结构紧凑、传动比大、承载能力大等优点,在汽车上得到了广泛应用。但行星齿轮的结构和工作状态复杂,其振动和噪声问题也比较突出[3],因此改善其噪声和振动,是车辆工程的重要研究课题之一。
以某款混合动力汽车合成箱 (在拉威娜行星齿轮机构上进行了优化及改进)为研究对象,建立动力传递系统的数学模型,进行扭转振动分析,计算系统固有频率,并在此基础上计算共振转速。
2 混合动力系统的结构与工作原理
该混合动力汽车传动系统由发动机、扭转减振器、大电机E2、小电机E1、复合行星排、二级减速轮、差速器、半轴和车轮等组成,结构示意图如图1所示。
复合行星排以拉威娜行星齿轮机构为基础,前排轮系包括小太阳轮、短行星轮、行星架以及齿圈,后排轮系包括大太阳轮、长行星轮以及与前排共用的短行星轮、行星架和齿圈,其中齿轮为斜齿轮。复合行星齿轮机构示意如图2所示。
不同于传统的拉威娜行星齿轮机构,该动力合成箱能增大后排轮系杠杆效能,降低电机峰值功率要求,进而降低电机的加工制造难度,并且节约成本[4~5]。
根据行星排与各动力源的连接方式,可计算得到发动机转速和齿圈输出轴转速分别为:
式中,nls为大太阳轮转速;nss为小太阳轮转速;i1为齿圈与小太阳轮齿数比;i2为齿圈与大太阳轮齿数比。
由式(1)和式(2)可知,发动机转速和车速相对独立。在车辆行驶过程中,可以通过调节大、小电机的转速和转矩实现无极变速,同时使发动机始终工作在最优化的工作区间。
3 传动系统扭转振动模型
3.1 固有频率的概念
固有频率是振动系统自身的物理属性,系统的振动特性由其固有频率决定。系统自由度的数目等于描述系统运动所必须的独立坐标的数目。一般情况下,n自由度系统的自由振动是由n个主振动组合而成的。在每个主振动中,系统各坐标之间有确定的比例关系,这种特定的振动形态称为主振型。n自由度系统有n种主振型,分别对应n个固有频率,所以多自由度系统的固有频率也叫主频率。当系统在正弦型激扰作用下,系统的强迫振动按扰频进行,当扰频与系统的任何一个固有频率相等时,系统发生共振,因此n自由度系统有n个共振频率[6~7]。
动力传动系统的扭振微分方程以矩阵的形式可写为:
式中,J为系统的转动惯量矩阵;C为系统的阻尼矩阵;K为系统的扭转刚度矩阵;θ为扭转振动角位移矢量;T为系统的激振扭矩矩阵。
在不考虑外部激励情况下,系统无阻尼自由振动可写成以下方程:
假定该系统为线性系统,则式(4)的解为:
式中,θm为线性系统初始角位移。
将式(5)代入式(4)后整理得:
根据线性代数的知识可知,只有当矩阵(K-ω2J)的行列式为零时,方程才有非零解。公式(4)的特征方程为:
根据式(7)求得的特征值就是扭振系统的固有圆频率,其对应的特征矢量就是该固有频率所对应的振型。
将动力传动系统各部分子系统的动力学方程组装成传动系统整体动力学方程,并以此求解传动系统的固有频率及振型。
3.2 传动系统动力学方程推导
基于样车传动系统质量和单行元件分布的特点,分析采用多自由度集中质量—弹簧的离散化建模方法。建模时应遵循以下简化原则:
a.相邻两集中质量间连接轴的刚度即为集中质量间的刚度,轴的转动惯量平均分配到相邻的集中质量上;
b.阻尼减振器可简化为有阻尼的扭转弹簧。该混合动力汽车传动系统扭振动力学模型如图3所示。
发动机、减振器和行星架部分动力学方程为:
式中,Je为发动机转动惯量;ktc=ktkc/(kt+kc),kt为减振器刚度,kc为行星架轴扭转刚度;θe为发动机角位移。
对齿轮副动力学模型,通常不考虑轴承和箱体等的弹性变形[8]。在不考虑行星架对行星轮支撑刚度的情况下,复合行星排的扭振动力学模型如图4所示。
根据拉格朗日方程[9]导出复合行星排的动力学方程组为:
其中,M′=diag(Jc,Js1,Js2,Ja1,Jb1,Ja2,Jb2,Ja3,Jb3,Jr1)
q=[θc,θs1,θs2,θa1,θb1,θa2,θb2,θa3,θb3,θr1]
K′为对称矩阵,其中
式中,Jc为行星架转动惯量;Js1为小太阳轮转动惯量;Js2为大太阳轮转动惯量;Ja为短行星轮转动惯量,且 Ja1=Ja2=Ja3;Jb为长行星轮的转动惯量,且Jb1=Jb2=Jb3;Jr为齿圈转动惯量;θc,θs1,θs2,θa1、θa2、θa3,θb1、θb2、θb3,θr分别为行星架,小太阳轮,大太阳轮,短行星轮 1、2、3, 长行星轮 1、2、3 和齿圈的角位移;ks1a为小太阳轮与短行星轮啮合刚度;ks2b为大太阳轮与长行星轮啮合刚度;kra为短行星轮与齿圈啮合刚度;kab为长行星轮与短行星轮啮合刚度;rca为短行星轮中心所在圆半径;rcb为长行星轮中心所在圆半径;rs1为小太阳轮基圆半径;rs2为大太阳轮基圆半径;ra为短行星轮基圆半径;rb为长行星轮基圆半径;rr为齿圈内齿基圆半径;an为行星齿轮机构法向压力角;B为行星齿轮分度圆螺旋角。
齿圈、二级减速轮和差速器的动力学方程为:
式中,Jm为二级减速轮转动惯量;θm、θd为二级减速轮、 差速器角位移;krm、kmd为啮合刚度;Rm1、Rm2、Rd为二级减速大小齿轮、差速器齿轮的基圆半径。
差速器、半轴和车轮部分的动力学方程为:
式中,Jd为差速器转动惯量;θlt、θrt为左、右车轮角位移;kla、kra为半轴扭转刚度。
左、右车轮的动力学方程为:
式中,Jlt、Jrt为左、右车轮转动惯量;θv为整车等效角位移;ktire为车轮扭转刚度。
整车等效动力学方程为:
式中,Jv=mvR2tire;mv为整车质量;Rtire为车轮滚动半径。
将式(8)~式(15)整合成系统特征方程:
式中,M为质量矩阵;K为刚度矩阵。
3.3 固有频率的计算
斜齿轮啮合刚度的计算较复杂,通过分析比较V.simmon的变形拟合公式[10]、石川公式法[11]以及简化公式法[12]3种方法得出的啮合刚度,采用通过简化公式方法求解的啮合刚度。
求解式(16)可以得到传动系统的固有频率。为提高传动效率和能量利用率,纯电动模式会锁止行星架,混合动力模式会锁止小太阳轮。2种模式下系统前几阶扭振频率如表1所列。
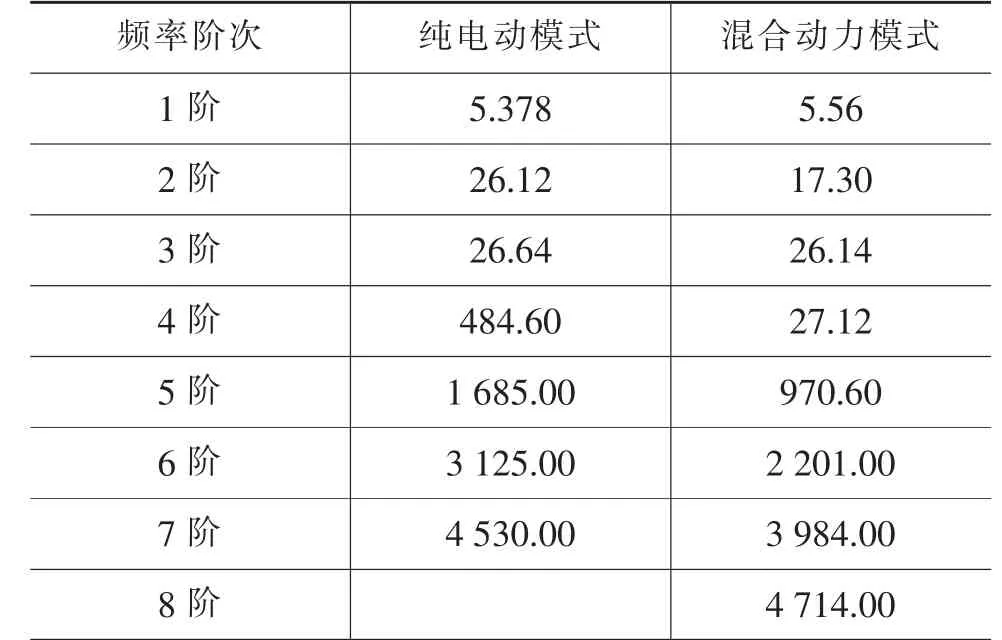
表1 扭转振动固有频率 Hz
4 共振转速的计算与分析
发动机输出的周期性激励扭矩是系统扭振的主要原因,当其转矩主谐量的频率与传动系统固有频率一致时,系统便产生共振[13]。该车辆采用四冲程四缸发动机,其2阶主谐量的激振最为重要[14],对应的发动机临界转速为:
式中,ft为传动系统固有频率。
引入发动机与大电机的转速比iel=ne/nl,不同的iel表示可能的不同运转工况。得到不同转速比和不同减振器刚度下的4阶低频临界转速脉谱图如图5所示。
由图5可知,当减振器刚度一定时,临界转速随着转速比变化而变化,在iel=1左右出现共振峰值;1阶临界转速与发动机的正常转速相差较远;2阶临界转速随减振器刚度增大而逐渐接近怠速范围;3阶、4阶临界转速与发动机怠速非常接近。因此,需要对大、小电机实施有效的转矩转速控制,尽可能增大发动机与大电机的转速差值,以避免共振;尽量选择较小刚度的减振器以降低共振转速,偏离发动机怠速范围。
5 结束语
a.推导了拉威娜行星齿轮机构动力学方程,在此基础上,建立了混合动力汽车传动系统的整体动力学模型。采用简单公式法计算出斜齿轮啮合刚度,且计算了纯电动模式与混合动力模式下传动系统的固有频率。
b.分析了不同转速比和减振器刚度变化下的共振转速特性。传动系统在转速比约为1时出现共振,且在一定范围内共振转速随减振器刚度增大而增大。通过大、小电机的转速转矩控制和选择小刚度的减振器,使共振转速远离发动机怠速范围,可以提高行驶平顺性和乘坐舒适性。
1 田光宇,彭涛,林成涛,等.混合动力电动汽车关键技术.汽车技术,2001(1):8~11.
2 饶振刚.行星齿轮设计.北京:化学工业出版社,2003.
3 巫世晶,任辉,朱恩涌,等.行星齿轮传动系统动力学研究进展.武汉大学学报,2010,43(3):398~403.
4 上海华普国润汽车有限公司,浙江吉利控股集团有限公司.双行星排四轴混合动力传动装置.中国,200910194470.5.2011-03-30.
5 刘钊,赵世琴,黄宗益.用杠杆模拟法建立行星变速器动力学模型.汽车工程,2000,22(4):274~277.
6 蔡仲昌,刘辉,项昌乐,等.车辆行星传动系统扭转振动固有特性及灵敏度分析.中国机械工程, 2011,22 (1):96~101.
7 Guo Y,Parker R G.Sensitivity of general compound planetary gear natural frequencies and vibration modes to model parameters.Journal of vibration and acoustics, 2010,132(1):1~13.
8 李润芳,王建军.齿轮系统动力学.北京:科学出版社,1997.
9 Ahmet Kahraman.Free torsional vibration characteristics of compound planetary gear sets.Mechanism and Machine Theory, 2001,36(8):953~971.
10 Simon V.Load and Stress Distributions in Spur and Helical Gears.ASME Journal of Mechanisms, Transmissions,and Automation in Design, 1988,110:197~202.
11 日本机械学会技术资料出版分科会编.齿轮强度设计资料.李茹贞,赵清慧译.北京:机械工业出版社,1984.
12 Calculation of load capacity of spur and helical gears-Application for industrial gears.ISO 9085:2002,2002,47~50.
13 喻凡,林逸.汽车系统动力学.北京:机械工业出版社,2008:134~137.
14 袁兆成.内燃机设计.北京:机械工业出版社,2008:160~175.
