倒棱工艺对激光角反射器衍射特性的影响

石 岩， 周 辉， 文 翔

(1．武汉大学电子信息学院，湖北 武汉430072;2．赵李桥中学，湖北赤壁437300)

式中:A为光线经过初次折射后的单位矢量;B，C和D分别为 A 矢量经过 i、j和 k 反射面(i、j、k=1，2，3)后的单位矢量;E为光线经过最终折射后的单位矢量;N0、N4分别为入射光线和出射光线的法线;N i、N j和N k分别为i、j和k反射面法线的单位矢量。Refr和Refl分别为矢量形式的折射和反射定律，它们可表示为:

0 引言

激光角反射器是具有定向反射特性的光学元件，其主要作用是增加接收机处的激光强度［1-3］。经激光角反射器衍射后的激光强度分布与激光角反射器参数以及光束入射条件有关［4-6］，受到目前激光角反射器加工工艺的限制，激光角反射器必然存在倒棱处理。在激光角反射器设计过程中，棱宽参数对衍射后的激光强度的影响往往被忽略［7-9］。事实上，由于倒棱工艺的出现会导致激光角反射器有效衍射区域发生改变，进而影响近场衍射和远场衍射强度分布规律，使得接收机所接收的激光强度出现不同程度的下降。因此，研究倒棱工艺对激光角反射器衍射特性的影响具有十分重要的意义。

本文从激光角反射器几何结构及倒棱方式出发，推导了激光角反射器有效衍射区域的数学模型，并结合激光角反射器的位相分布及衍射理论。分析了棱宽因素对激光角反射器近场和远场衍射特性的影响规律，并从量化角度给出了棱宽取值不同导致的衍射强度下降程度，为指导激光角反射器的设计提供了一定的参考价值。

1 激光角反射器有效衍射区域的分布模型

激光角反射器是由3个互相垂直的直角面及底面组成的实心四面体。当入射光束入射至激光角反射器内部时，光束先后经过底面的初次折射、3个直角面的反射和底面的最后折射，以6种不同次序从底面出射。

图1 激光角反射器坐标系

建立如图1所示的直角坐标系:以激光角反射器的顶点为原点，分别以激光角反射器的3条直角棱为x、y和z轴，称o-xyz坐标系为激光角反射器棱坐标系;以激光角反射器顶点在底面的投影o'为原点，以底面的法线方向为z＇轴方向，以y轴在底面的投影为y'轴，x'轴方向由右手螺旋法则确定。则o-xyz坐标系与o'-x'y'z'坐标系之间的转换关系为［10］:

式中:M为转换矩阵;a为激光角反射器的棱长。若激光角反射器底面采用圆形切割，则a =，r为激光角反射器底面圆半径。

若入射光在o'-x'y'z'坐标系下的入射角为φ，方位角为θ，则入射光矢量为

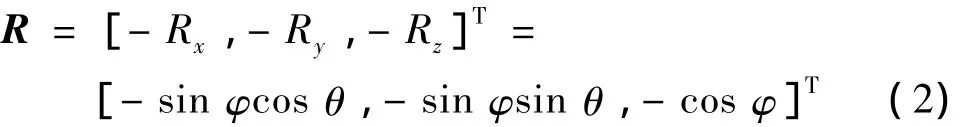
将该矢量转换到o-xyz坐标系，则入射光矢量方向可表示为

根据光线的折射和反射定律，可以得到在激光角反射器内部及出射后的光线矢量为［11］:

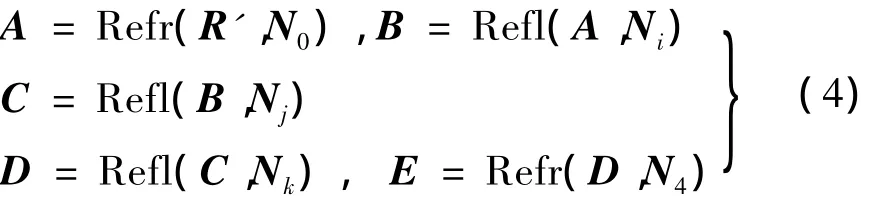
式中:A为光线经过初次折射后的单位矢量;B，C和D分别为 A 矢量经过 i、j和 k 反射面(i、j、k=1，2，3)后的单位矢量;E为光线经过最终折射后的单位矢量;N0、N4分别为入射光线和出射光线的法线;Ni、Nj和Nk分别为i、j和k反射面法线的单位矢量。Refr和Refl分别为矢量形式的折射和反射定律，它们可表示为:

若光束从空气入射至激光角反射器内部，n1=1，n2=n;相反，则n1=n，n2=1，n为激光角反射器材料的折射率。定义反射面1和2、反射面2和3以及反射面 3 和 1 之间的二面角偏差分别为 δ12、δ23、δ31，则反射面1、2和3的法线方向分别为:

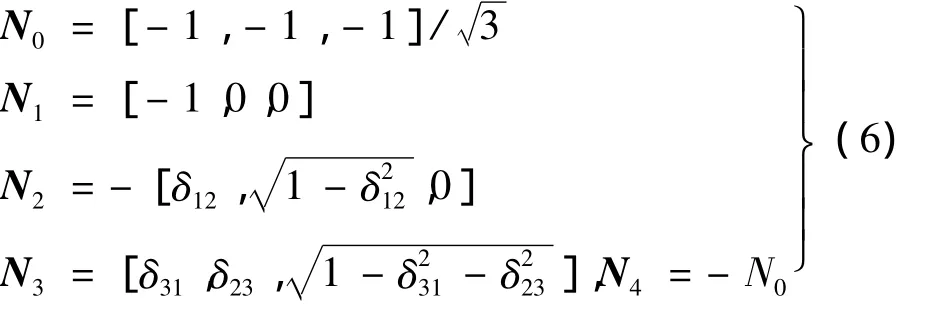
若入射光在o'-x'y'z'坐标系下入射光线与底面的交点为(xr'，yr'，0)，则在 o-xyz坐标系内的坐标为

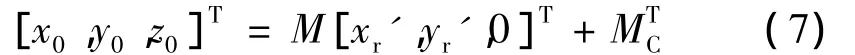
光线经过初次折射后分别与激光角反射器3个反射面相交，并最后从激光角反射器口径范围内折射出来，其交点坐标可以根据光线和反射面及折射面的方程得到，即:

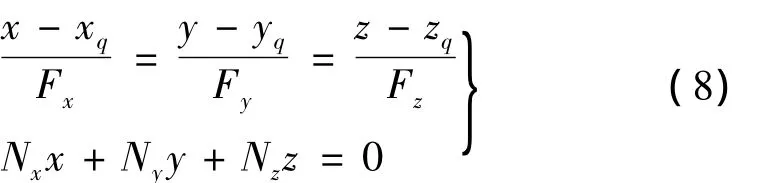
对于反射次序为 i，j，k的光线而言，坐标点(xq，yq，zq)分别表示光线与初始折射面以及 i，j，k反射面的交点，矢量 F=［Fx，Fy，Fz］分别表示入射至 i，j，k反射面和折射面的光线矢量，即为A至E矢量，N=［Nx，Ny，Nz］表示各反射面和折射面的法线矢量。

由于采用方程组(8)得到的折射面交点(x4，y4，z4)是在o-xyz坐标系内的，因此，为便于约束折射点的位置范围，将折射点坐标转换到o'-x'y'z'坐标系，则

［xc'，yc'，0］T=M－1{［x4，y4，z4］T－ MC} (9)

若激光角反射器底面采用圆形切割，并且进行了倒棱工艺处理，则各反射点和折射点位置必须位于激光角反射器的有效反射面和口径范围内，如图2所示。

根据图2中各折反射点与激光角反射器结构的关系，建立了它们与激光角反射器参数的约束区域表达形式，即:

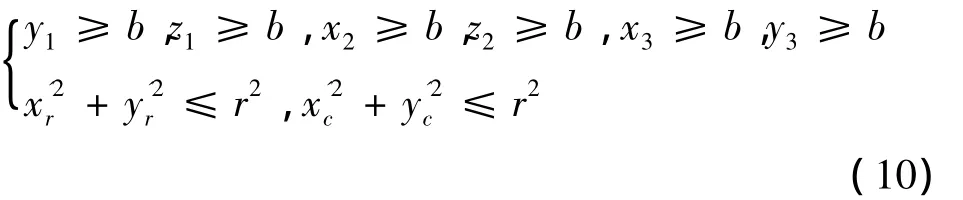
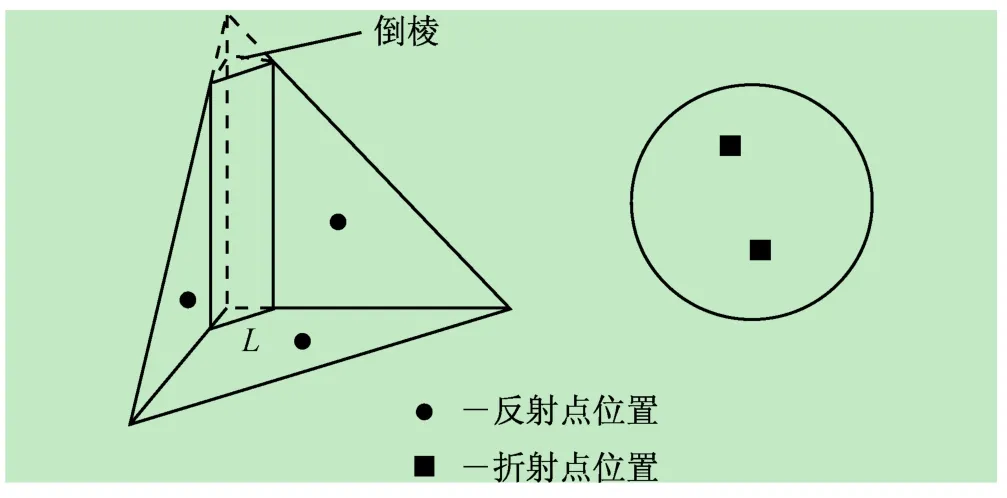
图2 折反射点区域示意图

激光角反射器的有效衍射区域与光束入射条件以及棱宽有着紧密的关系，对于圆形切割的角反射而言，若激光角反射器半径r=20 mm，材料折射率为1．461，则可以模拟出在不同光束入射条件下，不同棱宽对应的激光角反射器有效区域的变化规律，如图3所示。

图3 不同棱宽及光束入射条件下的激光角反射器有效衍射区域

从图3可以看出，当激光角反射器出现倒棱工艺时，激光角反射器的有效反射区域由6个相互分离的区域组成，并且随着棱宽的增加，6个区域的分离程度增加，这导致激光角反射器有效面积发生减小。当棱宽尺寸固定时，随着光束入射角的增加，6个区域的分离程度不变，但区域的面积变小。从衍射角度看，激光角反射器有效衍射区域直接影响其衍射的积分范围，倒棱工艺的出现必然导致激光角反射器衍射特性发生改变。

2 棱宽对激光角反射器衍射特性的影响

通常情况下，入射到激光角反射器口径范围内的光斑要远大于激光角反射器的口径，因此，入射到激光角反射器底面的光波可看作平面波，假设其振幅为1。若入射光倾斜入射至激光角反射器底面，则衍射光场中引入了倾斜因子，其计算公式可通过基尔霍夫衍射公式得到［12］:

式中:H为激光角反射器与接收机之间的距离;Σ因子为激光角反射器的有效衍射区域，它由光束入射条件和激光角反射器棱宽决定;φ为激光角反射器出射光波的位相分布［13］;k为波数;ρ为激光角反射器口径内任意一点到接收机范围内任意一点的距离。

根据激光角反射器口径大小以及激光角反射器与接收机之间的距离关系，可以将激光角反射器衍射分为近场衍射和远场衍射。对于圆形切割的激光角反射器，若H、r以及λ满足r2/λ＜H，则接收机处的衍射为远场衍射，否则为近场衍射［7］。考虑到激光角反射器加工过程中必不可免地存在二面直角误差，因此，选取高精度的5″激光角反射器作为分析对象，即二面直角误差约为 0．42″。

2．1 激光角反射器的近场衍射

采用菲涅尔近场衍射数学关系式并结合激光角反射器有效区域及位相分布，可模拟在不同棱宽和光束入射角条件下，激光角反射器近场衍射的分布规律。图4为仿真传输距离H为2 m时，棱宽和光束入射条件的改变导致激光角反射器近场衍射模式的变化。

图4 不同光束入射角条件下，棱宽对近场衍射分布规律的影响

图4 显示，棱宽的出现导致激光角反射器近场衍射分离成6个独立的衍射图样，每个图样的分布区域基本与激光角反射器有效衍射区域分布规律保持一致［14］。在倒棱位置处出现了近似狭缝的衍射图样，随着棱宽的增加，倒棱位置处出现更为暗的衍射条纹，这直接导致激光角反射器近场衍射总强度发生降低。同时，随着光束入射角的增加，倒棱位置处的衍射图样基本没发生变化，但考虑到激光角反射器近场衍射总强度的降低，因此，倒棱对近场衍射强度的降低比例减小。

由于激光角反射器近场衍射强度分布范围较小，接收机能够完全接收近场衍射的全部光强，因此，通常情况下，在接收机处于近场衍射范围时，以激光角反射器近场衍射的总强度为分析目标。图5给出了棱宽取值不同时，激光角反射器近场衍射总强度随光束入射角的变化规律(以垂直入射至理想激光角反射器的近场衍射总强度为1进行归一化)。

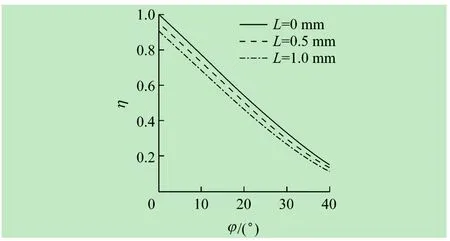
图5 棱宽取值不同时，近场衍射总强度及其随光束入射角的变化规律

从图5中看出，在不同的棱宽条件下，激光角反射器近场衍射总强度η随着光束入射角的增加呈递减趋势，并且棱宽值越大，递减趋势越剧烈。

图6模拟给出了在几种棱宽与棱宽为零对应的近场衍射总强度的差值Δη。表明随着光束入射角的增加，Δη逐渐减小。但是，对于某个固定的光束入射角，随着棱宽值的增加，Δη逐渐增加。在整个光束入射角范围内，当棱宽取值1 mm时，Δη最大值达到9．3%，而当棱宽取值0．1 mm时，Δη最大值仅为1．0%。

2．2 激光角反射器的远场衍射

图6 不同棱宽取值与棱宽为0对应的近场强度差值

当接收机位于激光角反射器的远场衍射位置处时，激光角反射器远场衍射图样的分布规律(以垂直入射至理想激光角反射器的衍射强度最大值为1进行归一化)与距离H无关。采用夫朗霍夫远场衍射公式并结合激光角反射器有效区域及位相分布，可模拟出在不同棱宽和光束入射角条件下，激光角反射器的远场衍射图样［15］。

为分析衍射图样中心点强度的变化情况，定义中心点强度的绝对下降量为d I=I2－I1，其中:I2为棱宽为零对应的中心点衍射强度;I1为存在倒棱时对应的中心点衍射强度，则相对下降量为RI=d I/I2。

图7模拟了光束垂直入射条件下棱宽对激光角反射器远场衍射强度的影响。

图7 棱宽为0的激光角反射器远场衍射图样

从图7可以看出，当光束垂直入射到激光角反射器表面时，由于二面直角误差的存在，其远场衍射图样不再是艾里斑分布，衍射图样中心点的光强发生下降，并且衍射强度的分布范围也发生扩散。

当存在倒棱工艺时，衍射图样中心点的强度将进一步下降。图8显示了棱宽取值为0．3 mm与棱宽为0时所对应的衍射图样差异的分布。解算结果表明，衍射中心点的光强绝对下降量为2．4%，相对下降量为3．3%。随着棱宽的增加，其下降程度将更加明显。

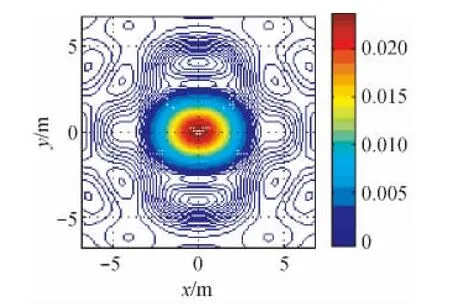
图8 棱宽为0与棱宽为0．3 mm的激光角反射器远场衍射图样的差异

事实上，当光束倾斜入射到激光角反射器表面时，棱宽导致激光角反射器远场衍射强度的降低程度与垂直入射时的也不相同。图9模拟了光束入射角为20°时棱宽对激光角反射器远场衍射强度的影响。

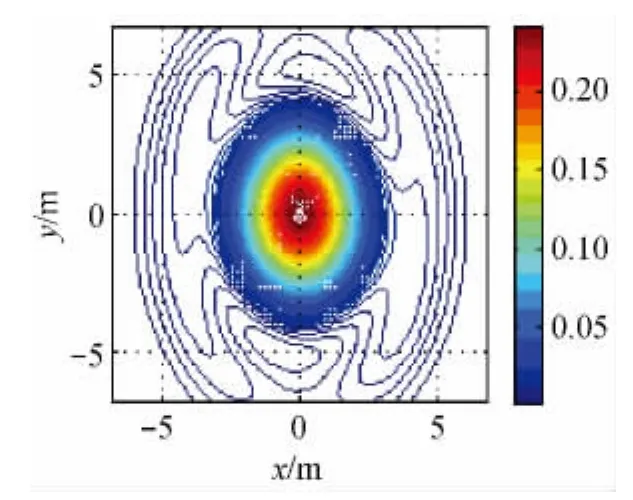
图9 棱宽为0的激光角反射器远场衍射图样

图9 表明，当光束倾斜入射至激光角反射器时，激光角反射器远场衍射图样重新进行分布，衍射图样中心点光强发生下降。

当存在倒棱工艺时，衍射图样中心点的强度将进一步下降。图10模拟了入射为20°时，棱宽为0与棱宽为0．3 mm的激光角反射器远场衍射图样的差异。从图10中可以看出，当棱宽为0．3 mm时，衍射图样接收机中心点的光强绝对下降量为2．1%，相对下降量为8．5%，这是因为光束倾斜入射时衍射图样中心点的强度发生下降所导致的。

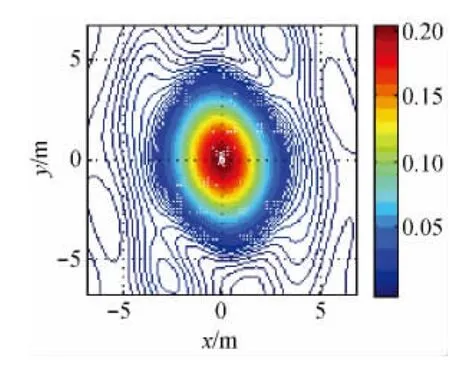
图10 棱宽为0、0．3 mm的激光角反射器远场衍射图样的差异

由于接收机往往仅能接收到远场衍射图样中心位置附近的光强，因此，以远场衍射图样中心点的光强为分析对象，模拟在棱宽取值不同时，中心点强度I0随光束入射角的变化规律，具体如图11所示。

图11 棱宽取值不同时，衍射图样中心点光强随光束入射角的变化规律

图11 显示，在不同的棱宽条件下，随着光束入射角的增加衍射图样中心点强度I0迅速减小，并且棱宽值越大，递减趋势越剧烈。

图12模拟给出了几种棱宽与棱宽为0对应的衍射图样中心点强度差值ΔI0随光束入射角的变化。结果表明，随着光束入射角的增加，绝对差值ΔI0逐渐减小。但是，对于某个固定的光束入射角而言，随着棱宽值的增加，绝对差值ΔI0逐渐增加。在整个光束入射角范围内，当棱宽取值为0．1 mm时，强度的绝对下降量最大值达到1．2%，相对下降量最大值为8．9%。当棱宽增加至1．0 mm时，强度的绝对下降量最大值达到12．0%，相对下降量最大值为50．3%。

图12 几种棱宽与棱宽为0对应的衍射图样中心点强度差值随光束入射角的变化规律

事实上，若激光角反射器二面直角误差取值不同，会导致衍射图样的发散程度不同，使得衍射图样中心点的强度值发生变化，则棱宽对衍射图样中心点的影响程度也不相同。二面角误差越小，衍射图样中心点强度值越大，棱宽对其影响程度也越明显，反之亦然。

3 结语

由于激光角反射器倒棱工艺的出现，使得激光角反射器衍射特性发生了改变，直接影响接收机处的激光强度，因此，从量化角度研究倒棱大小对衍射强度数值的影响是十分必要的。本文以激光角反射器有效衍射区域为基础，利用激光角反射器位相分布和衍射理论，仿真分析了不同棱宽对激光角反射器近场衍射总强度及远场衍射图样中心点强度的影响规律。所得结论为限定激光角反射器的倒棱宽度提供了有益的理论依据。

［1］ Andersen P H，Aksnes K，Skonnord H．Precise ERS-2 orbit determination using SLR［J］．Journal of Geodesy，1998，72(8):421-429．

［2］ Currie D，Agnelloc S D，Monache G D．A lunar laser ranging retroreflector array for the 21st century［J］．Acta Astronaut，2011，68，667-680．

［3］ 耿 涛，赵齐乐．基于全球激光观测资料的COMPASS-M1轨道质量评定［J］，武汉大学学报，2009，34(11):1290-1292．

［4］ Neubert R．Preliminary design of the laser retroreflector for the CHAMP satellite［C］//Proc 10th Workshop on Laser Ranging Instrumentation．Shanghai，1996:216-222．

［5］ Dement＇ev V A，Lamekin P I，Chernov S M．Fraunhofer diffraction at a nonideal corner reflector with flat faces［J］．Journal of Optical Technology，2005，72(11):837-842．

［6］ 陈 浩，谭久彬．光束入射角对角锥合作目标激光测距的影响［J］．光电子·激光，2006，17(8):986-988．

［7］ 李 亮，孙华燕．机载光学角反射器阵列的结构设计［J］．四川兵工学报，2012，33(11):117-119．

［8］ 李建超，高 明，苏俊宏．机载角反射器阵列设计［J］，应用光学，2011，32(5):835-839．

［9］ 周 辉，李 松，郑国兴．常见卫星激光角反射器阵列结构的设计［J］．红外与激光工程，2009，32(4):692-697．

［10］ Li S，Tang B，Zhou H．The calculation on diffraction aperture of cube corner retroreflector［J］，Chinese Optics Letter，2008，6(11)，833-836．

［11］ Zhou H，Li S，Zheng Guoxing．The phase mode of reflected beam from laser retroreflector with dihedral angle and flatness error［J］．Optical Review，2011，18(1):1-6．

［12］ 梁铨廷．物理光学［M］．北京:机械工业出版社，1986:165-166．

［13］ 周 辉，李 松，郑国兴，等．卫星激光角反射器精度对远场衍射模式的影响［J］．光学学报，2009，29(1):60-66．

［14］ 周 辉，李 松，郑国兴，等．卫星激光角反射器有效区域的研究［J］．光子学报，2009，38(8):1920-1925．

［15］ 钟声远，徐广平，吴 键．卫星激光角反射器的远场衍射光强研究［J］．激光与红外，2009，39(2):128-136．