呼和浩特东站站台雨棚结构设计与分析
2013-09-02蔡玉军
蔡玉军
(中铁第一勘察设计院集团有限公司,西安 710043)
呼和浩特东站站台雨棚结构设计与分析
蔡玉军
(中铁第一勘察设计院集团有限公司,西安 710043)
以呼和浩特东站站台雨棚为工程案例,详细介绍大跨张弦梁的设计过程。应用SAP2000和ANSYS有限元分析软件,分别对张弦梁整体结构和单榀构件进行分析,两者计算结果吻合较好;结合工程特点,提出合理的吊装方案,确保了张弦梁张拉和吊装过程的安全。最后对张弦梁支座节点进行了分析,设计出新型支座节点,并对节点进行数值模拟分析,结果满足要求。
站台雨棚;张弦梁;节点设计
1 工程概况
呼和浩特东站是京包线上重要的交通枢纽和大型客运中心。站台雨棚对称布置于主站房两侧,每侧站台雨棚的平面尺寸均为108.50 m×208.34 m,雨棚总覆盖面积39 900 m2。雨棚屋面最低点距轨面15.35 m,最高点距轨面18.80 m。雨棚顺股道方向柱距23.382 m,垂直股道跨度分别为54.0 m、48.5 m。站房两侧雨棚总长为200 m,为减少温度应力的影响,每侧雨棚各设置1道伸缩缝将雨棚分为长度不大于100 m独立单元。图1、图2为呼和浩特东站站房及雨棚整体鸟瞰图和站台雨棚内视图。

图1 站房及雨棚整体鸟瞰图

图2 站台雨棚内视图
2 结构选型及结构体系布置
受站场条件限制,站台雨棚在垂直于股道方向设置3列雨棚柱,柱顶与钢箱梁连接形成纵向钢框架,以增强雨棚纵向的整体刚度和抗震性能;雨棚屋面采用连续张弦梁结构体系,每跨张弦梁采用一端固定铰支座、一端滑动铰支座的连接方式简支于钢梁顶面,如图3所示。为了减小地震作用下屋面体系对同一榀钢框架的水平力,两跨张弦梁的固定铰分别设置于不同柱列,即PA-PB跨张弦梁固定铰及滑动铰分别置于PB、PA列雨棚柱,PB-PC跨张弦梁固定铰及滑动铰分别置于PC、PB列雨棚柱。顺股道方向每23.382 m柱距间等分布置4榀张弦梁,每榀张弦梁支座处均设置有分叉柱,有效地降低了纵梁的竖向变形,保证每榀张弦梁的协同工作。

图3 雨棚剖面(单位:mm)
PA-PB轴张弦梁跨度为 54.0 m,跨中矢高6.0 m,上弦压杆采用□700×300×18×20 mm 箱形截面,下弦拉索采用121φ5 mm高强低松弛平行钢丝束;PB-PC轴张弦梁跨度为48.5 m,跨中矢高5.5 m,上弦压杆采用□650×300×18×20 mm箱形截面,下弦拉索采用109φ5 mm高强低松弛平行钢丝束;张弦梁腹杆均采用φ273 mm×8 mm圆钢管,上端与张弦梁上弦铰接,下端通过铸钢节点与拉索连接。由于屋面自重较轻,在风吸力作用下下弦索会发生松弛,甚至失效的现象,为了保证下弦索始终处于张紧状态,在上弦箱形截面内灌入水泥砂浆以增加结构配重[1]。
单榀张弦梁在平面内可形成独立的稳定体系,并满足施工及正常工作的受力要求,而其平面外的刚度较差,上弦受压极易失稳,几乎不能形成稳定的结构受力体系。因此,在每榀张弦梁间采用水平支撑和刚性系杆进行连接,以形成稳定的空间结构,保证张弦梁的正常受力性能[2-3],雨棚标准单元结构平面布置如图4所示。
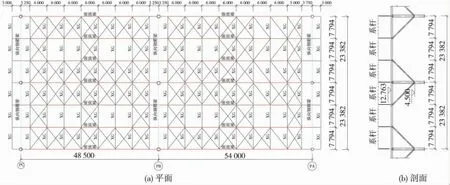
图4 雨棚结构布置(单位:mm)
3 设计荷载取值及工况组合
设计荷载是结构分析的重要依据,取值是否合理将直接影响到结构的安全性和经济性。工程中考虑的荷载有永久荷载:结构自重、屋面围护自重、吊顶及设备自重等;可变荷载:屋面活载、雪荷载、风荷载;另外还应考虑地震作用和温度效应。
3.1 荷载标准值
(1)永久荷载:结构杆件自重由计算程序自动导算,屋面围护及吊顶荷载取值为0.5 kN/m2。
(2)可变荷载:标准值0.5 kN/m2。
(3)雪荷载:标准值0.45 kN/m2(按100年一遇取)。
(4)风荷载:由于雨棚结构跨度大、刚度小、自振周期长,在随机风荷载作用下可能会引起较大的风振效应,同时受站房体型的影响,雨棚屋面各点的体型系数和风振系数已无法按《建筑结构荷载规范》(BG50009—2001)进行选取[4]。因此,设计中风荷载值根据风洞试验报告进行取值[5]。
(5)地震作用:本工程抗震设防烈度为8度,设计地震分组为第一组,设计基本地震加速度为0.20g。
(6)温度作用:由于张弦梁一端为固定铰支座,另一端为滑动铰支座,温度作用对结构的受力影响不大[6]。但由于张弦梁滑移端的变形量对支座构造要求较高,因此温度效应仍作为重要的荷载工况进行计算。计算温差取全年最热月及最冷月的平均温度与结构张拉环境温度的差值,温差分别取为+25℃、-35℃(结构张拉环境温度为10~15℃)。
3.2 荷载工况组合
荷载工况组合考虑了上述各项荷载[7],同时参考了相关实际工程[8-9];为了保证张弦梁在风荷作用下的结构安全,设计中增加了1组下弦索应力控制组合,保证张弦梁在最不利的组合工况下仍具有一定的拉力。各荷载工况组合如表1所示。
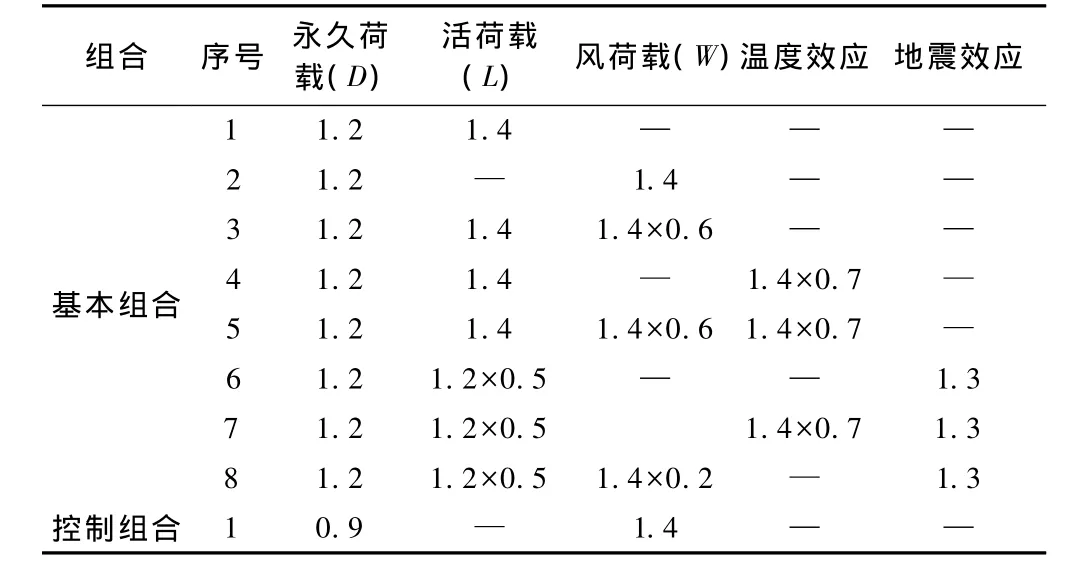
表1 荷载工况组合

图5 张弦梁结构前3~5阶结构振型
4 结构计算分析
4.1 结构内力计算
结构分析采用通用有限元软件 SAP2000 V15.1.0对整体结构进行计算,同时采用ANSYS有限元软件对单榀张弦梁进行了分析,并和SAP2000计算结果进行对比。张弦梁上弦选用空间梁单元、屋面支撑及张弦梁竖向腹杆采用两端释放转角自由度的梁单元、下弦索采用没有刚度和微小质量的梁单元进行模拟。根据文献[1-10],由于张弦梁结构在荷载态分析时,考虑几何非线性效应的分析结果和线性分析结果非常接近,因此该类结构荷载态的分析可不考虑几何非线性的影响,即符合小变形假定;但在张拉阶段,即结构由零状态至初始状态的过程中,结构会出现较大的变形,因此结构按几何非线性进行分析。
由于张弦梁一端滑移,因此模型前2振型均为张弦梁屋盖的整体平动振型,张弦梁结构的前3~5阶结构振型如图5所示(以下以PA-PB跨张弦梁为例进行计算结果分析)。从结构振型看,在前几振型中均未出现张弦梁平面外的水平振动,说明张弦梁间设置的水平支撑及刚性系杆起到了重要的支撑作用。因此,对于大跨张弦梁结构体系设置这样的刚性支撑是非常必要的,设计时要给予特别的重视,且应有一定的安全储备。典型荷载工况下的位移及变形如图6所示。

图6 典型工况下结构变形
计算结果如下:(1)张弦梁上弦杆受力较均匀,最大应力比0.80。(2)下弦拉索中最大拉应力为750 MPa。(3)结构在永久荷载标准值作用下产生的竖向最大挠度为122 mm,挠跨比(f/L)为1/442,满足屋面竖向挠度变形限值要求,可见在合理的矢高比和较强的平面外支撑条件下,张弦梁结构具有较好的竖向刚度。(4)在水平地震作用下,柱顶水平位移21 mm,柱顶位移与柱高比值为1/840;而在风荷载作用下,柱顶水平位移达到58 mm,柱顶位移与柱高比值为1/306。通过对比发现,由于PA-PB跨张弦梁屋面曲率并不对称,在垂直于屋面的风荷载作用下,屋脊两侧屋面的风荷载水平分量不能相互抵消,因此荷载水平分量差值导致屋面产生了整体的水平推力,从而使柱顶产生了较大的水平位移。由此可见,在张弦梁结构选型的过程中应尽量避免不对称的情况产生。
在整体分析的基础上,利用ANSYS有限元分析程序对单榀张弦梁进行了校核计算,张弦梁在1.0D+1.4L+0.7T工况下的上弦梁内应力及下弦拉索应力如图7所示。在各工况下,张弦梁上弦梁最大应力比为0.70,下弦索最大拉应力为600 MPa。可见 ANSYS分析结果较SAP2000计算结果偏小,经分析发现,导致这一结果的原因是SAP2000整体模型分析时,上弦梁的变形受到屋面水平支撑的约束,导致下弦索张拉力增大,从而使得结构体系内力增大。但结构变形及应力分布与整体模型吻合较好,从而验证了计算结果的准确性。
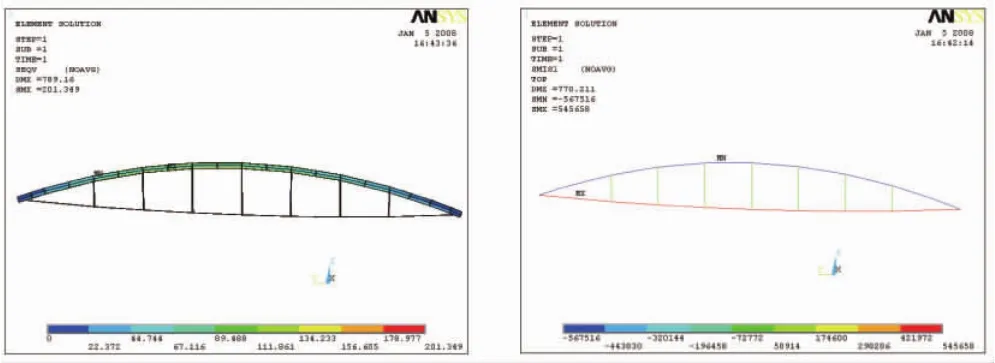
图7 单榀张弦梁ANSYS分析结果
4.2 结构吊装
张弦梁的张拉和吊装是张弦梁结构施工的重点和难点,在施工前应对张弦梁进行施工阶段的验算,以确定张弦梁的张拉次数和结构找形。由于本工程中张弦梁上弦为单根矩形截面梁,平面外刚度完全由屋面支撑体系提供,因此在初张拉和吊装过程中须保证每榀张弦梁的平面外稳定。若在单榀张弦梁张拉和吊装过程中通过平衡索保证其平面外的稳定,不但使得张拉过程变得复杂,而且给施工增加了难度。考虑到施工的安全和易操作性,同时参考类似工程的施工经验[11-12],将两榀张弦梁及部分水平支撑作为吊装单元在地面胎架上进行初张拉,以保证结构平面外的稳定,如图8所示。待初张拉完成后再进行整体吊装,柱顶就位后再进行二次张拉,此时结构已具有一定的平面内、外的刚度,保证了张拉和吊装过程的安全。

图8 张弦梁吊装单元
5 节点设计
由于受纵向支承梁截面宽度和下弦索张拉端的限制,成品支座难以满足工程的需要,因此针对张弦梁张拉节点和支座节点的特点构造出了新型节点。张弦梁下弦索通过销轴与连接耳板相连,保证拉索在张拉过程中可以自由变形;连接耳板插入上弦梁内与翼缘焊接连接,上弦梁腹板在支座处通过厚板过渡,与支座处的双耳板通过销轴连接;为了保证支座构造与计算模型中滑动节点相吻合,在连接端板底面设置有聚四氟乙烯滑移材料,满足支座在荷载作用下的滑移要求,同时在滑移方向和垂直方向上设置有滑动挡板和抗拔件,防止极端荷载工况下张弦梁滑落或支座拔起,张弦梁端部构造节点如图9所示。为了确保支座节点的复杂受力安全,在理论计算的基础上应用ADNA有限元软件对节点进行了模拟分析,分析结果如图10所示。
由分析结果可以看出:

图9 张弦梁支座节点(单位:mm)

图10 张弦梁支座分析结果
(1)支座节点模型分析中应力值均较小,均处于材料的线弹性范围内,完全满足工程安全要求。这与支座具有一定的平动滑移能力有很大关系,建议在类似大跨度结构中,支座节点可以采用类似方式进行处理,不但可以大幅度减小下部结构的水平受力负荷,还可获得更好的经济性与安全性;
(2)在销轴和销孔的接触位置,产生了应力集中现象,应力值较大且应力分布变化剧烈。经分析认为原因有:一是数值计算模型中对该部分采用了接触边界以及接触网格,会带来一定的影响;二是在实际工程中,该位置是支座传力的关键部位,受力较大。因此,销轴和销孔设计时应留有一定的强度余量,同时为了减小由于接触表面不平滑产生的应力集中以及应力侵蚀对接触面的影响,对销轴和销孔的表面应进行硬化处理,并采用一些特殊成孔工艺。
6 结论
呼和浩特东站站台雨棚采用了连续大跨张弦梁结构体系,计算分析表明,张弦梁结构用于较大跨度的站房雨棚建筑中,可充分发挥其优导的结构性能,并能较好地实现建筑的外观造型。经过合理的结构设计,按屋面投影面积计算,主体结构用钢量仅为75 kg/m2,与类似工程相比极大地节省了结构用钢量,取得了较好的经济效果,并实现了经济和美观的统一。
通过以上分析可知,张弦梁结构体系的水平地震作用效应并不明显,但对于风荷载效应却很敏感,因此在设计过程中对风荷载的取值应慎重,同时对有风荷载参与的组合工况应全面;张弦梁的施工顺序对张弦梁的受力性能及施工安全影响较大,因此在张弦梁施工过程中应针对不同工程特点制定合理的张拉、吊装方案;张弦梁支座节点的构造对结构是否安全、合理起着至关重要的影响,因此,在设计过程中对支座节点应作为重点进行研究,必要时可进行数值模拟分析,以确定节点区的应力分布,确保结构的安全、可靠。
[1] 黄明鑫.大型张弦梁结构的设计与施工[M].济南:山东科学技术出版社,2005:9-13.
[2] 刘锡良.现代空间结构[M].天津:天津大学出版社,2003:14-21.
[3] 姜子钦,何志军,丁洁民.座边界及屋面支撑对张弦桁架结构施工过程影响分析[J].结构工程师,2011(6):99-105.
[4] 蒋凡.车站无站台柱雨棚风荷载设计探讨[J].铁道标准设计,2011(5):94-96.
[5] 武汉大学结构风工程研究所.呼和浩特火车站风洞试验与抗风性能分析报告[R].武汉:武汉大学结构风工程研究所.
[6] 张雷.张弦梁结构施工模拟及温度影响研究[D].北京:北京建筑工程学院,2006:77-78.
[7] 中华人民共和国建设部.建筑结构荷载规范(2006年版)[S].北京:中国建筑工业出版社,2002:6-9.
[8] 傅学怡.国家游泳中心水立方结构设计[M].北京:中国建筑工业出版社,2008:31-45.
[9] 徐培福,傅学怡,等.复杂高层建筑结构设计[M].北京:中国建筑工业出版社,2005:109-117.
[10] 吴祖成,楼文娟,高子聒,等.单向张弦梁结构的受力性能研究[J]. 钢结构,2010(7):1-3.
[11] 闫宇.延安火车站钢结构雨棚张弦梁[J].铁道建筑技术,2010(2):95-99.
[12] 康亚强,唐虎.大连北站无站台柱雨棚设计[J].铁道标准设计,2011(3):93-95.
[13] 范峰,支旭东,沈世钊.黑龙江国际会议展览体育中心主馆大跨钢结构设计[M].北京:中国计划出版社,2002:806-811.
Structure Design and Analysis on Platform Canopy of Hohhot East Railway Station
CAI Yu-jun
(China Railway First Survey and Design Institute Group Ltd.,Xi'an 710043,China)
Taking the platform canopy at Hohhot East Station as a project case,this paper introduces the design process of a beam string structure(BSS).Using SAP 2000 and ANSYS finite element analysis software,the whole BSS and the BSS members were analyzed respectively,and both calculation results could accord well with each other.Combined with the characteristics of beam string structure,the feasible hoisting scheme were put forward which could ensure the safety of beam string structure in the processes of tensioning and hoisting.Finally the bearing joint of the beam string structure was analyzed,and a new type of bearing joint was designed.Through numerical simulation analysis on the joint,it is concluded that the design can meet the relevant requirements.
platform canopy;beam string structure;joint design
TU318
A
1004-2954(2013)04-0101-04
2012-08-10;
2012-08-30
中国铁道建筑总公司科研项目(20114287-K3-191)
蔡玉军(1980—),男,工程师,2007年毕业于长安大学结构工程专业,工学硕士,E-mail:caiyujun727@163.com。
