基于PLC的温度控制仿真试验平台设计

祁 鲲 厉 虹

（北京信息科技大学自动化学院，北京 100192）

工业生产过程中，温度控制十分常见，特别是在钢铁冶炼、化工精馏、生物发酵、药品生产等工业生产中占有非常重要的地位[1-4]，然而温度控制具有非线性、纯滞后、大惯性、难以准确控制的特点，传统控制方法调节时间长、超调大、控制精度低，在温度控制精度要求较高的场合无法达到理想的控制效果；同时一些较为复杂的先进控制算法，如遗传算法、预测控制、模糊控制、神经网络控制等，能够获得较好的控制效果[4-11]，但内容抽象，理论性强，缺乏相应的试验研究平台。为此本文设计了基于PLC（可编程控制器）的温度控制仿真试验平台，并在Visual Basic编程环境下建立了监控界面。

1 试验平台基本结构

基于PLC的温度控制系统原理如图1所示，包括PLC、输出控制电路、加热炉、温度检测电路等部分；在自动化程度较高的场合，设置了上位计算机进行系统监控。其中，输出控制电路根据PLC输出值实现对燃气阀开度或燃料输送量的控制；温度检测部分一般为温度传感器及其转换电路，将检测到的实际温度值传送给PLC。在本试验平台中，采用OMRON CP1E型PLC实现控制算法；作为被控对象的加热炉则由上位机在 Visual Basic编程环境下仿真实现，参数可以根据实际情况设定；相应的输出控制电路和温度检测电路则由PLC和上位机之间的直接数据交换替代。

图1 温度控制系统原理图

2 监控界面设计

考虑对各类PLC的兼容性，试验平台基于Visual Basic编程环境设计了上位机监控界面。该界面提供友好的人机交互功能，如参数设定、数据显示、曲线绘制、数据存储等。如图2所示，整个界面分为图像区、参数设置与数据显示区、命令发布区、系统说明区四个部分。界面的最上方是图像区，包括温度曲线实时绘制、加热炉模型示意、温度计动画显示等。在界面中部的参数设置与数据显示区可进行加热炉模型参数（K、TD、τ）和控制系统参数（TC、T）的设定，并可以实现设定温度、当前温度、误差温度的实时显示。命令发布区可发布不同的命令以实现相应的控制：“加热炉模型阶跃响应”键将自动绘制系统所设定加热炉模型的阶跃响应曲线，可作为控制器设计的参考；“仿真控制”键可调用平台自身基于Visual Basic实现的控制程序进行仿真控制（这里预设了大林算法控制程序，用户可自行修改），可对比验证控制器设计效果；“PLC控制”键将调用在PLC控制器中所设计控制程序的运行数据进行显示。系统说明区在界面的下方，对系统信息如加热炉模型的传递函数、期望的闭环控制系统传递函数以及上位机与PLC的数据交换地址等进行说明。该界面力求形象生动、信息完整，具有良好的可视性、操作性、通用性。

图2 监控界面

3 加热炉对象模拟

其差分方程为

式（2）即为加热炉的差分模型。根据此方程可在 Visual Basic编程环境下实现对加热炉模型的仿真模拟。试验平台计算子程序流程图如图3所示。

图3 计算子程序流程图

4 控制范例

如文献[1-3，10-11]所述，基于PLC的温度控制算法有很多，本文以大林算法为例实现温度控制。1968年Dahlin针对工业生产过程中遇到的含纯滞后控制对象提出了一种具有消除余差和对纯滞后有补偿作用的算法。大林算法的设计准则是，以大林算法为核心的数字控制器，使闭环系统的特性为具有时间滞后的一阶惯性环节，且滞后时间与被控对象的滞后时间相同[12]。

大林算法在PLC中实现的流程如图4所示。需要注意的是，为实现精确控制，应在PLC中采用浮点运算，但是在PLC与上位机的参数传递中整型数据较为方便和快捷，因此数据发送方可以将含有小数的数值在数据传递前扩大一定的倍数，然后作为整型数据传递，数据接收方收到数据后再将数据缩小相同的倍数以恢复原值。

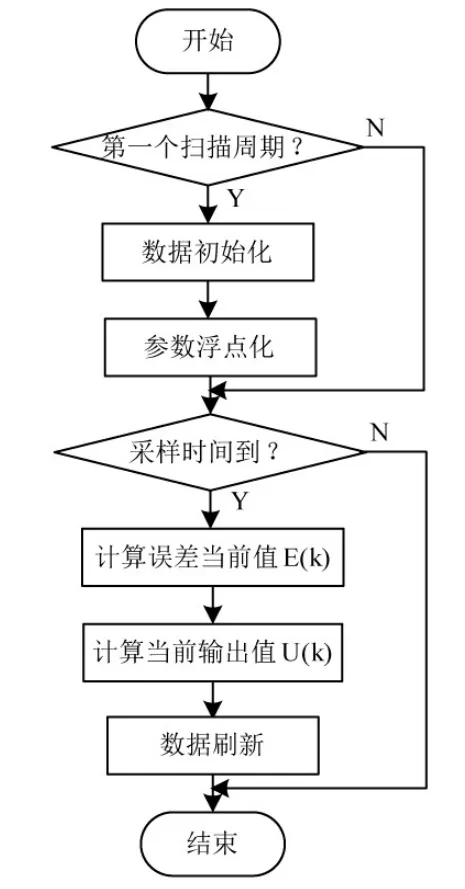
图4 基于PLC的大林算法流程图

在试验平台中设置系统参数如下：加热炉模型纯滞后时间常数τ=5s，比例系数K=100，惯性时间常数TD=10s；期望的闭环控制系统惯性时间常数TC=2s；系统采样周期T=0.1s。将设定温度分别设置为200℃、360℃时运行PLC大林算法控制程序，得到的温度曲线截图如图5（a）、（b）所示，其超调量分别为 0.8℃和 1.3℃，温度调节稳态误差均为0.0℃。从运行结果可以看出，将大林算法应用于基于PLC的加热炉温度控制系统中，响应速度快，超调量小，稳态温差小；并且其控制系统结构简单，根据需要可以很好的应用到工业控制中。

图5 大林算法温度控制响应曲线

5 结论

该试验平台充分利用 Visual Basic的软件优势开发了基于PLC的温度控制系统监控界面，使之具有良好的可视性、操作性；并且Visual Basic语言具有较好的通用性，能够很方便的实现与其他类型PLC或其他控制器的兼容。本文给出了大林算法温度控制范例，达到了较好的控制效果；同时该平台还可以用来实现其他先进控制算法如模糊控制、神经网络控制等，具有一定的开放性。

[1] 刘增环,王利珍,何广祥.加热炉炉温 PLC模糊控制系统的设计[J].自动化与仪表,2011,26(10)：27-30.

[2] 陈曦,赵德瑞,吕湘晔.S7-300 PLC在精馏塔温度控制系统中的应用[J].自动化仪表,2011,32(3)：39-41.

[3] 杨德,畅福善,沈俊霞.基于 PLC的发酵罐温度控制系统[J].自动化与仪表,2012,27（5）：33-35.

[4] KELIANG ZH, HONGYAN Y.Application of fuzzy predictive-PID control in temperature control system of freeze-dryer for medicine material[C]//2011 Second International Conference on Mechanic Automation and Control Engineering (MACE),2011： 7200 -7203.

[5] PENG X H, MO ZH,XIAO L SH.Research and application on GA-Based Two-Stage fuzzy temperature control system for a type of industrial furnace[C]// 2010 International Conference on Electrical and Control Engineering (ICECE),2010：1558-1561.

[6] ZANG H Q,LI Q.The automatic temperature system with fuzzy self-adaptive PID control in semiconductor laser[C]//IEEE International Conference on Automation and Logistics(ICAL),2009：1691-1694.

[7] 陈东升,高俊侠,胡科堂.一种远程温度控制系统的设计及应用[J].实验技术与管理,2011,28(7)：72-74.

[8] 宋云霞,朱学峰.大时滞过程控制方法及应用[J].化工自动化及仪表,2001,28(4)：9-15.

[9] 王春亮,李茜.Fuzzy-smith 控制器在温度控制中的应用[J].自动化与仪表,2011,26(12)：41-43.

[10] 李硕,李鹏阳.基于PLC的退火炉温度控制系统[J].计算机工程,2010,36(5)：245-247.

[11] 郑华,方赟,杨晓梅.基于单神经元与 PLC的温度控制系统设计[J].自动化与仪表,2011,26(9)：31-35.

[12] 赖寿宏.微型计算机控制技术[M].北京：机械工业出版社,2012.