谐振接地系统单相接地故障暂态特性分析

姚丽宝 黄世远

（1.福州省电力有限公司宁德电业局，福建 宁德 352100；2.福建省电力有限公司检修分公司，福州 350013）

谐振接地系统具有较高的供电可靠性，但长时间带单相接地故障运行将影响电力系统的安全运行[1]，因此在发生接地故障后，需尽快准确的选出故障线路。

利用单相接地故障时产生的暂态信号来判断故障线路是近年来故障选线研究的主要方向。根据所利用的暂态特征，主要可分为两类：①利用暂态过程的时域特征[2-3]，此为传统的选线方法；②利用故障时零序网络中线路的相频特性，这是研究的新方向[4-6]。但目前上述两种方法均存在明显缺点：①传统基于简化模型分析所得的暂态时域特征结论不尽完善，特别对接地点过渡电阻的影响考虑不足，因此对大电阻接地故障的选线准确率不高；②现有基于线路相频特性所得的暂态零序容性电流的分布规律适应度有限，特别是对越发广泛使用的缆-线混联传输线适应度较小，导致该方法的准确性和灵敏度大为降低[7-8]。

针对上述问题，本文在时域上研究了故障电压初相角、过渡电阻对暂态特征的影响，在频域上通过分析各种结构线路输入阻抗的相频特性，确定了暂态零序容性电流在不同类型传输线路上的分布规律。

1 暂态接地电流时域特征

1.1 谐振接地系统等值回路

暂态接地电流通常认为由故障相电压骤降引起的放电电流和非故障相电压骤升引起的充电电流两部分组成。本文仅研究充电电流的暂态过程，系统简化模型如图1所示[9]。

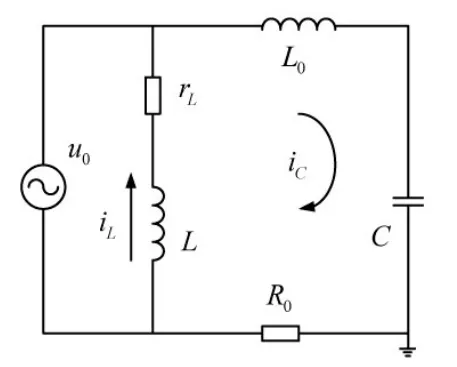
图1 谐振接地电网单相接地等值回路

图中，u0为零序电源电压；rL，L分别为消弧线圈的有功损耗电阻和电感；L0为零序回路的等值电感；R0为零序回路中的等值电阻；C为电网三相对地电容总和。

由图 1，根据叠加原理，暂态接地电流id可认为由暂态电容电流iC和暂态电感电流iL叠加而成。计算iC时，通常认为自由振荡频率较高的iC对电感具有阻隔作用，且由于L＞＞L0，从而忽略L，即忽略iL，直接由L0、C、R0组成的串联回路和作用于其上的零序正弦电源电压u0，经时域分析求得iC。iL可由非线性电路的基本理论导出。则由iC和iL叠加而成的id表达式为

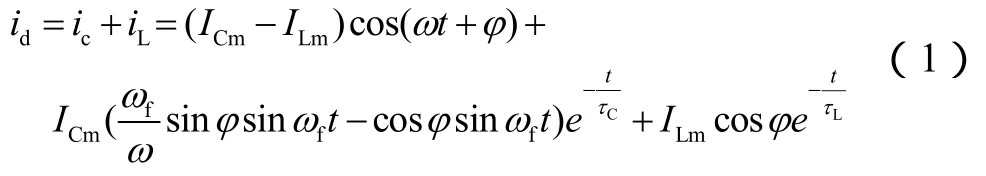
式（1）又可分解为两部分：①由第一项单独构成的接地电流稳态分量；②由第二项电容电流的暂态自由振荡分量与第三项电感电流的暂态直流分量之和构成的接地电流暂态分量。

分析暂态分量表达式可知，振荡分量与直流分量的幅值均决定于故障电压初相角，且二者成逆向分布关系。振荡分量的最大值出现在初相角为 90°的奇数倍时，此时直流分量约等于 0；直流分量的最大值则出现在初相角为180°的偶数倍时，此时振荡分量可忽略不计。

1.2 仿真模型

利用Matlab的PSB搭建谐振接地系统的分布参数模型如图2所示，其中线路1和线路3分别为由10km电缆和 10km架空线路组成电缆-架空混联线路及架空-电缆混联线路，线路2为长10km的架空线路，线路4为长10km的电缆线路。图中架空线路正、零序参数为：R1=0.17Ω/km，C1=0.00969μF/km，L1=1.21 mH/km，R0=0.23Ω/km，C0=0.008 μF/km，L0=5.478 mH/km；电缆线路正、零序参数为：R1=0.27Ω/kmC1=0.339μF/km，L1=0.255mH/km，R0=2.7Ω/km，C0=0.028μF/km，L0=1.019 mH/km；消弧线圈补偿度为5%。

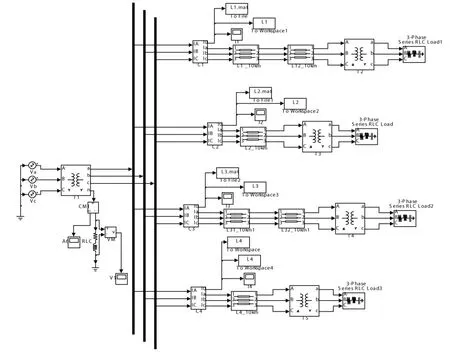
图2 谐振接地系统仿真模型

1.3 故障初相角对暂态特征的影响

因受篇幅限制，本文仅列举相电压过峰值和过零点两个典型时刻来分析故障初相角对暂态电流的影响。设在A相电压相角分别为270°（相电压过峰值）和0°（相电压过零点）时，线路4在距母线1km处发生单相接地故障，接地电阻1Ω，仿真得各馈线的暂态电流分别如图3和图4所示。

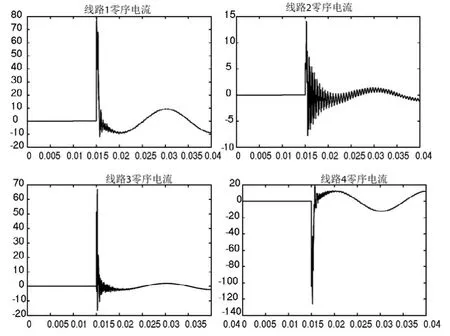
图3 初相角270°时各馈线暂态电流

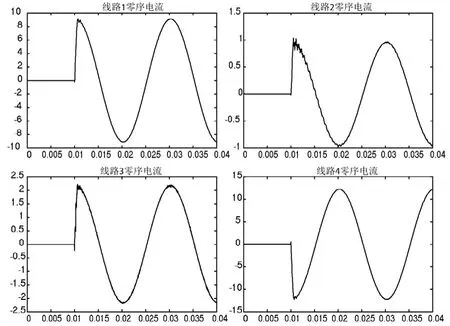
图4 初相角0°时各馈线暂态电流

经分析不同故障初相角的仿真结果，可得以下结论：①故障发生在相电压过峰值时，所有馈线暂态电流均明显存在一个含有大量高频振荡分量的暂态过程，当故障发生在相电压过零点时，馈线暂态电流中基本不存在振荡分量，以直流分量为主，此结果与前文分析一致；②架空线路的振荡频率较含电缆馈线的小得多，说明线路结构对暂态电流频谱具有影响；③故障线路暂态电流幅值最大，健全线路中含有电缆的线路幅值大于纯架空线路的幅值，说明线路参数对暂态电流幅值具有影响；④故障线路暂态电流与健全线路极性相反。

1.4 故障点过渡电阻对暂态特征的影响

过渡电阻对暂态电流的影响包括直接影响与间接影响。直接影响是指过渡电阻直接影响暂态分量幅值，过渡电阻越大，暂态电流幅值越小。间接影响是指过渡电阻通过暂态电流幅值间接影响电容充电速度，幅值越大，充电越快，电容电流的振荡频率越高，反之亦然。由此分析可知，受过渡电阻对电容电流振荡频率的影响，1.1节中所求得的暂态接地电流必然仅适用于一定大小的过渡电阻。根据电力系统分析可知，式（1）仅适用于以下两种情况：

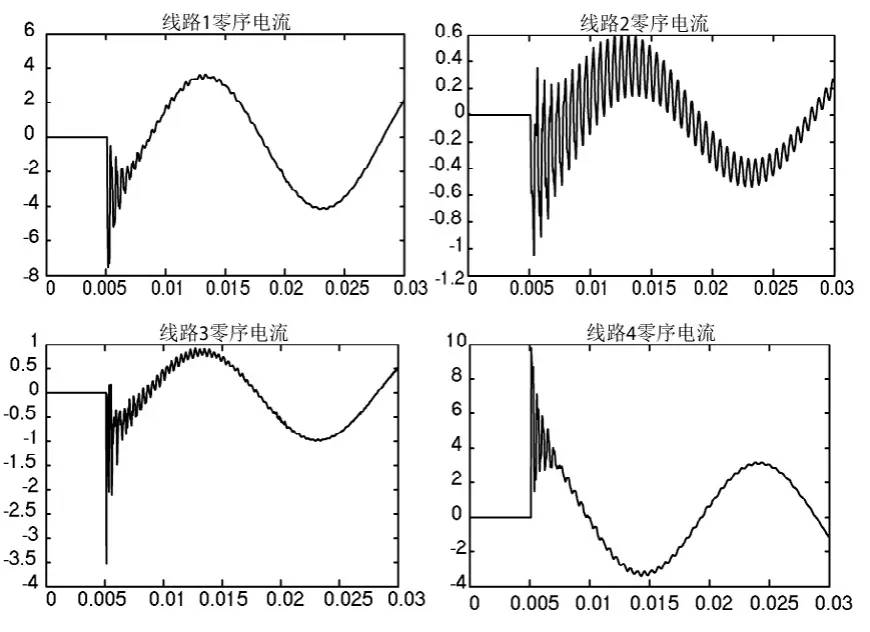
图5 过渡电阻较大时线路暂态电流

而对于更大的过渡电阻，因暂态电容电流振荡频率过低（最低可至工频），将不可忽略L对C的作用。为求此过渡电阻的大小，可忽略L0及rL，由L与C组成的并联回路求得，过渡电阻需满足。此时，系统处于欠阻尼状态，其暂态电流如图6所示，呈周期性振荡衰减。

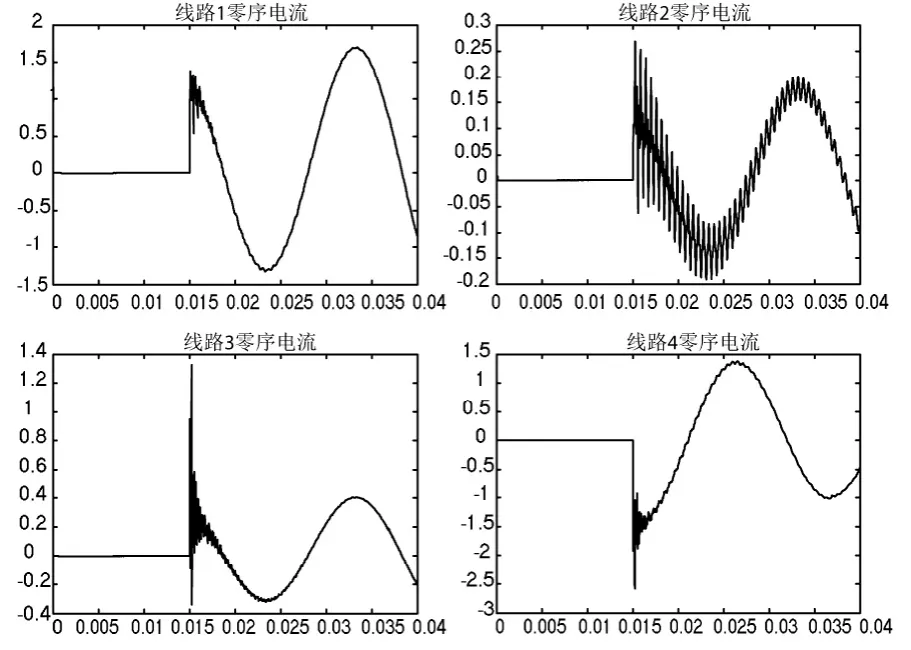
图6 大过渡电阻时线路暂态电流

多次仿真结果还表明，R0越大，暂态电压首半波、幅值与第二个半波幅值比值将越小，如图7所示。

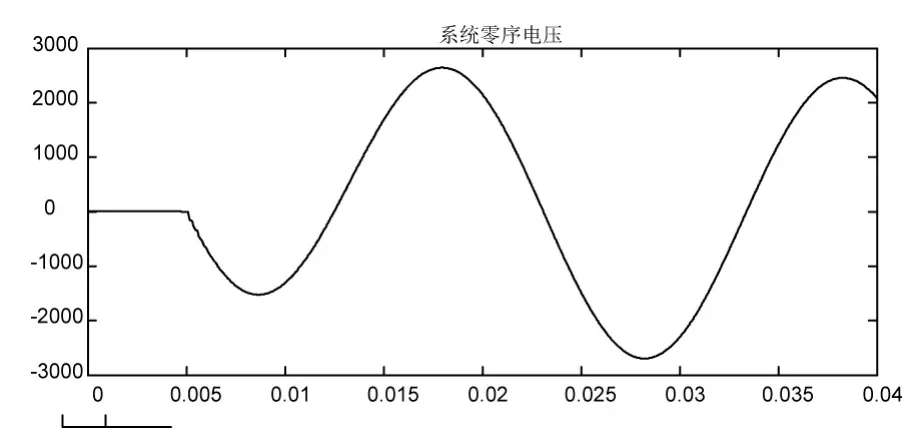
图7 系统暂态电压

2 暂态接地电流频率特征

2.1 基于线路分布参数的故障模量模型

从时域分析暂态电流实现了对暂态过程的宏观了解，但从上述分析过程可发现时域分析方法存在以下两个明显缺点：

1）电感对系统的影响收频率作用明显，若对频率大小考虑不足，一概通过忽略电感来简化系统模型，可能因此得出与实际情况相反的结论。

2）仅片面的从时域分析暂态特征，完全抛弃了对系统频率特征差异的分析，这对于结构复杂的系统，极可能因不正确使用故障信息而导致选线错误。

因此上述从时域分析暂态电流所得的结论显然存有不足，很有必要继续从频域分析暂态接地电流在不同频段上的特性，以进一步完善暂态电流特征。为此，线路自身电感及消弧线圈电感均必须予以考虑。利用卡伦包尔变换，依据故障分析原理和叠加原理，可得从故障点看到的基于线路分布参数模型的系统故障零序网络等效图[10]，如图8所示。

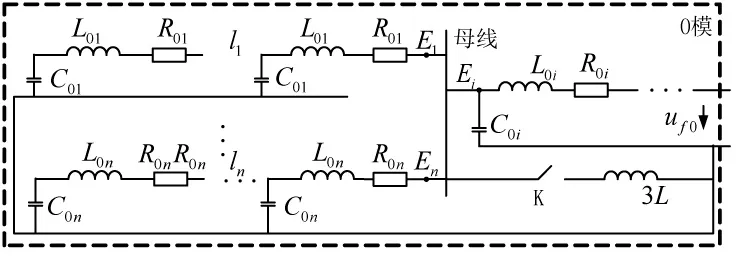
图8 基于线路分布参数的故障零序网络等效图

此图是从频域分析暂态接地电流特征的基础，图中，L0k、C0k、R0k、Ek、lk分别为馈线k的单位长度零序电感、单位长度零序电容、单位长度电阻、检测点及馈线长度；L为消弧线圈自身等效电感；开关K控制中性点接地方式，对于谐振接地系统K为闭合。

2.2 谐振零序网暂态相频特性分析

随着城市建设的快速发展，目前城市配电网已不再仅由架空线路构成，而是同时采用了架空线路、电缆线路以及电缆与架空线相混联的复杂线路，以下针对这些应用中常见的线路类型进行分析。

1）健全线路暂态相频特性分析

为获得在检测点处检测到的线路等效阻抗，可依据二端口网络原理，将图8中任意一条健全线路k末端看做开路，再利用传输方程求得。

对于单一均匀传输线路，包括架空线路和电缆线路，其等效阻抗表达式为

忽略较小的线路电阻，将ω=2πf带入式（2）可得阻抗Z0ck关于f的函数：

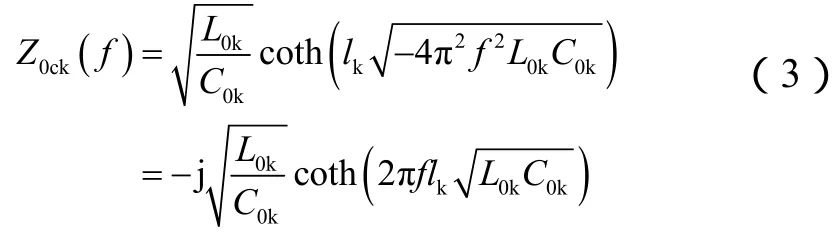
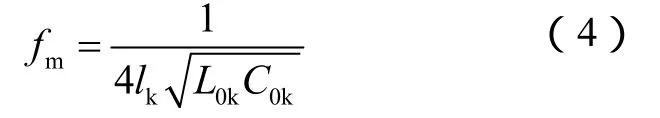
由式（4）可知，对于单位长度零序电感及零序电容大小相等的线路，线路越长，fm越小；对于长度相同的线路，单位长度零序电感或零序电容越大，fm越小。

对于母线出线处为电缆，后转架空线路的电缆-架空混联线路，等效阻抗表达式为

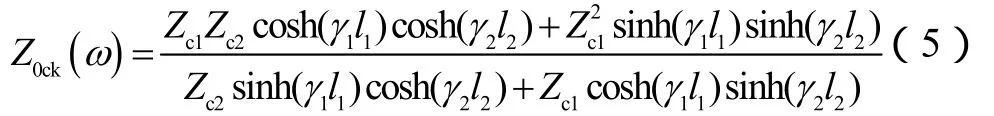
式中，各参数意义与式（2）相同，下标1，2分别表示电缆线路和架空线路。

对于母线出线处为架空线路，后转电缆的架空-电缆混联线路，线路输入阻抗表达式为

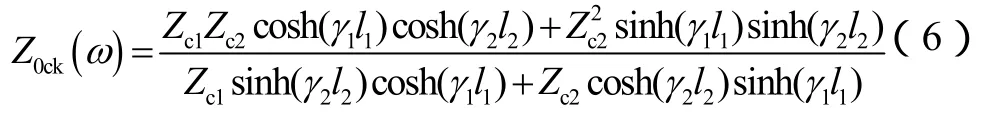
对于其他结构线路，可同理推得其等效阻抗表达式，这里不再继续给出。但显然线路结构越复杂，其相应等效阻抗表达式也越复杂。根据所得等效阻抗，研究中利用Matalb获得相应的相频特性图。

由式（2）、式（5）及式（6）可知，影响输入阻抗的因素包括线路参数及线路结构。据此，分以下三类进行仿真：①长度分别为10km和20km的架空线路，相频特性如图9（a）所示；②长度均为10km的架空线路和电缆线路，相频特性如图9（b）所示；③均由10km电缆和10km架空线路组成的电缆-架空混联线路和架空-电缆混联线路，相频特性分别如图 9（c）、9（d）所示。

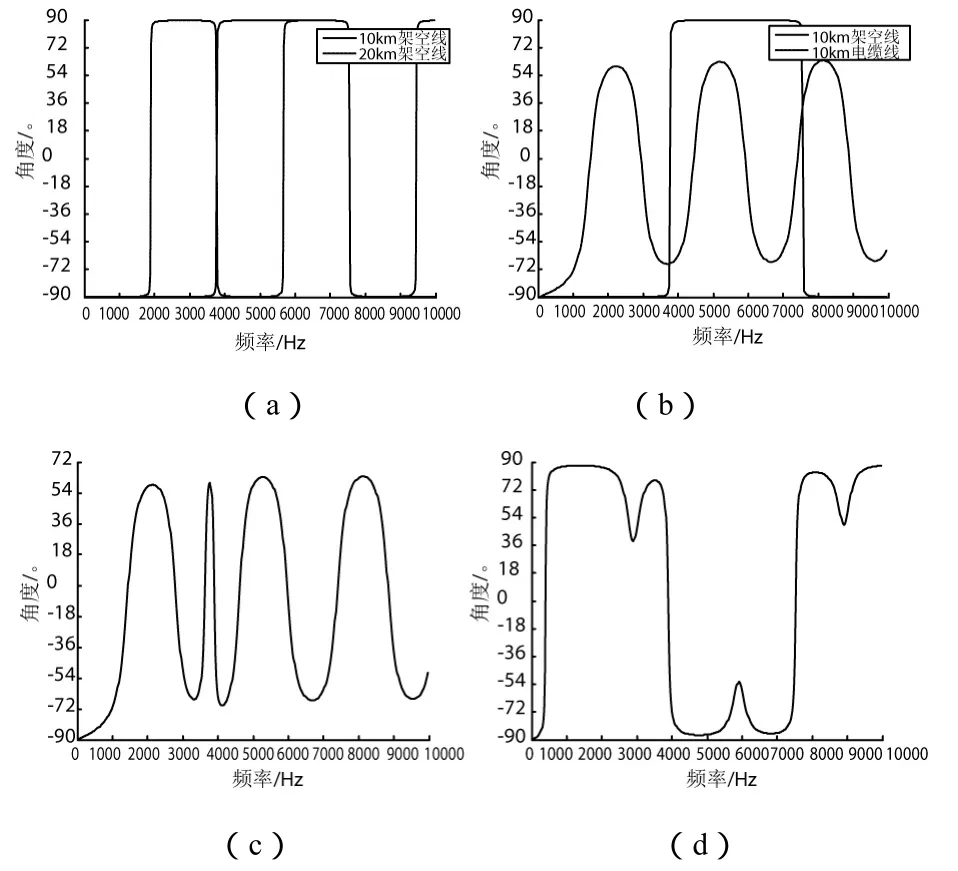
图9 不同条件下线路的相频特性

针对首次发生串联谐振的频率fm及相频特性波形两个主要特征，通过比较图9的各子图可得如下结论：①20km架空线路具有的fm明显小于10km架空线路的fm，电缆线路因单位长度零序电容远大于架空线路，故10km电缆线路的fm远小于同长度架空线路的fm，这些与前文分析一致；②架空线路的容性频段阻抗角等于-π/2，感性频段阻抗角等于π/2，波形总体为一方波，而电缆线路的相频特性总体类似正弦波；③电缆-架空混联线路的fm决定于该线路中电缆段线路的fm，与架空段线路无关，波形较不规则；④架空-电缆混联线路的fm较同长度电缆-架空混联线路的fm小的多，波形更显不规则。

2）故障线路暂态相频特性分析

与健全线路检测点检测的是本线路等效阻抗不同，故障线路检测点检测的是故障线路背后所有线路并联的总等效阻抗。对于谐振接地系统，故障线路检测到的导纳应为所有健全线路及消弧线圈的并联导纳（采用导纳表示可使表达式简洁），即

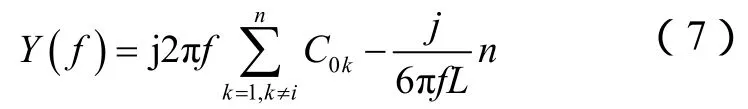
式中，C0k表示健全线路等效集中电容，n表示健全线路的总条数。因此该导纳的相频特性势必较任意一条健全线路都更为复杂，具体表现为：①串联谐振由任意一条健全线路的串联谐振引起，故其fm等于所有健全线路fm的最小值fmmin；②并联谐振由所有健全线路之间的并联谐振引起。

轮流以线路1、2、3、4为故障线路，得到的故障线路检测点的背后阻抗相频特性如图10顺序所示。

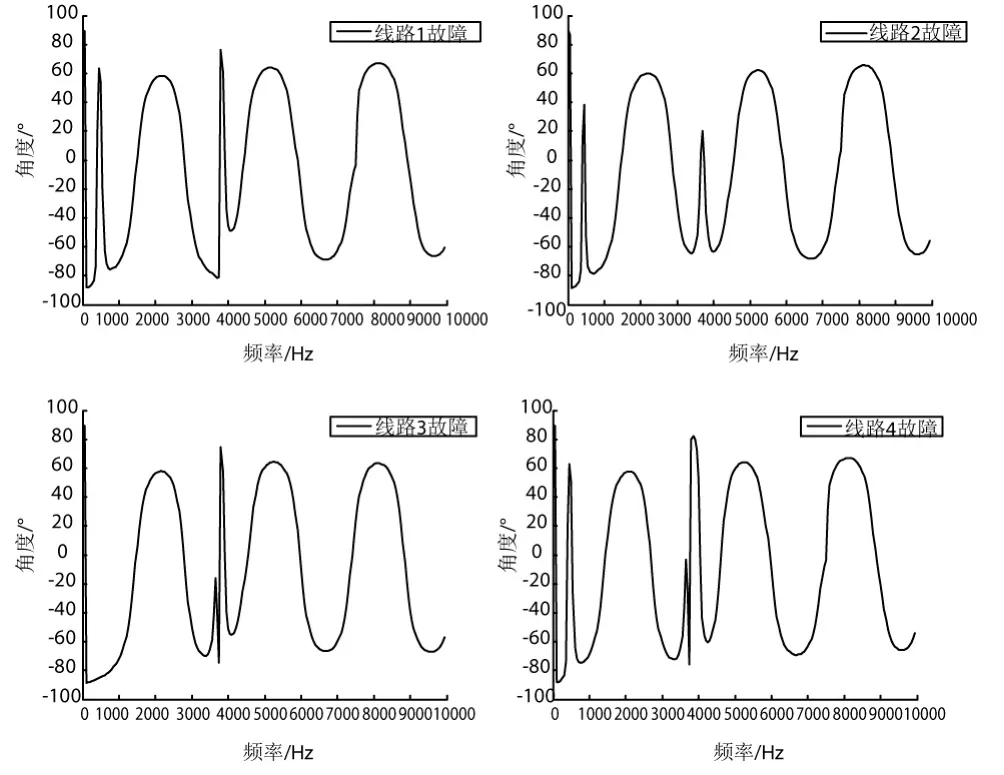
图10 故障线路检测点相频特性

将图9与图10结合比较可知：①消弧线圈仅对故障线路的相频特性产生影响，且仅使首个容性频段之前产生一次并联谐振。设首次并联谐振频率为fB，最大值fBmax在具有最大等效集中电容C0k的线路发生故障时取得；②从首个并联谐振之后的相频特性波形完全决定于健全线路的串并联谐振，总体复杂无规则，这与前文分析一致。

2.3 选定频段（SFB）的确定

由上述分析，谐振接地系统的 SFB可定义为fBmax到fmmin的频段。在SFB范围内，所有线路（包括健全线路和故障线路）检测点检测到的等效阻抗均为容性阻抗，从而可简化图8为图11所示。

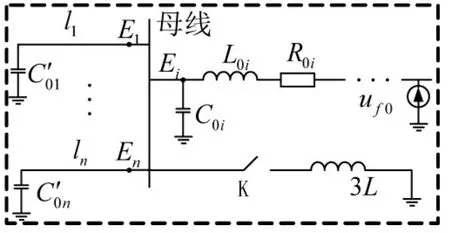
图11 故障时SFB内零序网络等效图

根据图11，在SFB内所有健全线路暂态电流极性相同，而与故障线路极性相反，且故障线路的暂态零序电流幅值等于所有健全线路幅值之和，这与从时域分析所得结果一致。但在SFB之外，因健全线路之间存在谐振的可能，即健全线路阻抗不再恒定同为容性或感性，此时前面的分析结论不再恒定成立，这也再次验证了分析暂态频域特征的必要性。

结合稳态分析结论，显然暂态零序电流在 SFB内的特性与稳态一致。因此在且仅在SFB内，从暂态过程到稳态过程，即在故障后的所有时间内，均有以下结论：对于谐振接地系统，当线路发生单相接地故障时，故障线路和健全线路暂态零序电流极性相反，故障线路的零序电流幅值等于所有健全线路幅值之和；当母线发生单相接地故障时，所有线路零序电流都由母线流向线路，极性相同。

3 结论

根据电力系统故障分析的一般知识，本文首先从时域上分析了谐振接地系统在发生单相接地故障后，故障初相角和接地电阻对系统零序暂态特征的影响。由于利用简化模型从时域分析暂态过程所得结论不尽完善，甚至有一定错误，故又从频域上详细分析了现有配电网中广泛采用的各种结构线路等效阻抗的相频特性，确定了谐振接地系统的 SFB。最后，通过综合故障后的暂态电流时、频特征和稳态时域特征，进一步确定了在不同类型传输线路上暂态零序容性电流的分布规律。经Matlab仿真实验，验证了所得结论的正确性，为下一步更准确利用暂态分量进行故障选线打下了坚实理论基础。

[1] 要焕年,曹梅月.电力系统谐振接地[M].北京：中国电力出版社,2000.

[2] 操丰梅,苏沛浦.小波变换在配电自动化接地故障检测中的应用研究[J].电力系统自动化, 1999,23(13)：33-36.

[3] 龚林春,黄挚雄.基于小波包的小电流接地故障选线仿真研究[J].计算机科学与工程, 2008,30(3)：103-105.

[4] 王伟,焦彦军.暂态信号特征分量在配网小电流接地选线中的应用[J].电网技术,2008, 34(4)：96-100.

[5] 薛永端,冯祖仁,徐丙垠.中性点非直接接地电网单相接地故障暂态特征分析[J].西安交通大学学报, 2004,38(2)：195-199.

[6] 王耀南,霍百林,王辉,等.基于小波包的小电流接地系统故障选线的新判据[J].中国电机工程学报,2004,24(6)：54-58.

[7] 潘露,吕艳萍,于芳,等.基于相频特性与多频带分析的小电流接地系统故障选线[J].电力系统自动化, 2007,31(4)：76-79.

[8] 张伟刚,张保会.中性点非直接接地系统零序网络的相频特性[J].电力自动化设备,2010,30(3)：71-75.

[9] 张艳霞,王清亮.应用故障暂态特性实现配电网故障选线的新方法[J].电力系统自动化,2009,33(16)：76-80.

[10] 张新慧.基于Prony算法的小电流接地故障暂态选线技术[D].山东：山东大学,2008.