高等数学研究性教学方案探析
2013-08-30葛倩李秀珍
葛倩,李秀珍
(山东建筑大学理学院,山东 济南 250101)
0 引言
近年来,在国家人才发展总战略的指导下,教育部在《关于进一步加强高等学校本科教学工作的若干意见》中,特别提出“积极推动研究性教学,提高大学生的创新能力”[1],本科研究性教学逐步成为高等教育教学改革的一个热点。研究性教学以培养学生的认知能力和创新能力为主要特征,它不同于以单向性知识传授和知识积累为主的传统教学,在课堂教学中,强调发挥教师的主导作用和学生的主体作用,是“以类似于科学研究的方式组织教学和引导学生获取、运用知识并培育学生创新精神、提高学生实践能力的一种新型教学模式”[2]。研究性教学实质上就是研讨式教学、启发式教学和参与式教学。教师以学生的知识积累和教学内容为基础,引导学生创造性地运用所学知识,积极主动地发现问题、分析问题和解决问题;学生在研究过程中积累知识,锻炼思维,培养能力,而不是被动地接受教师的灌输。研究性教学将传统的注重教师“教”转变为注重学生“学”,充分挖掘学生潜能,增强学生的学习主动性,而教师是学习的组织者与参与者[3]。高等数学是一门基础课程,很大程度上影响着学生整个大学的学习,在高等数学教学中实施研究性教学,对于培养学生的创新精神,提高学生的数学素养,促进学生专业课的学习,都有着十分重要的作用。我们在课堂教学、教学实践、教学资源、教学评价等方面对高等数学研究性教学的实施进行了探索和改革,努力构建一个立体化的高等数学教学新模式。
1 高等数学研究性教学问题分析及方案设计
课堂教学是教学中最重要的一个环节,研究性教学意味着创新、发现与创造,因此应着眼于教学生学会学习,从强调依靠教师“教会”,转变为引导学生“学会”,并使学生“会学”,从而培养学生的创新能力,夯实学生“终身学习”的基础。高等数学的教学就是一个发现问题、分析问题、解决问题的过程,是一个经验、理解和反思的研究过程,强调以学生为主体的学习活动对学生理解数学的重要性[4]。教学活动是师生积极参与、交往互动、共同发展的过程,教师应该站在学生的角度,与学生一起互动研究。
1.1 发现问题
高等数学中的许多概念都有着广泛的应用背景,因此,在学习一个新知识之前,可先由老师把实际问题提出来,引导学生思考,激发学生的学习兴趣。比如在讲解曲率的时候,我们先结合“4.28胶济铁路火车脱轨”的实际问题,提出“火车为何在弯道处脱轨”的问题,进一步通过分析铁轨的弯曲程度与最高限速的关系、拱桥主拱圈弯曲程度与荷载等级的关系,提出“如何衡量曲线的弯曲程度”这一数学问题,从而引入曲率的概念。
1.2 分析问题
分析问题的过程是一个步步深入的过程,教师要扮演一个引导者、合作者的角色,可以通过问题组的方式给学生指明方向,引导学生类比和归纳,体验数学发现的过程[5],让学生在解决问题的过程中不断建构和完善自己的知识体系,以达到教学目标的要求。
比如在给出曲率的概念推导曲率计算公式的过程中,我们是这样引导的:
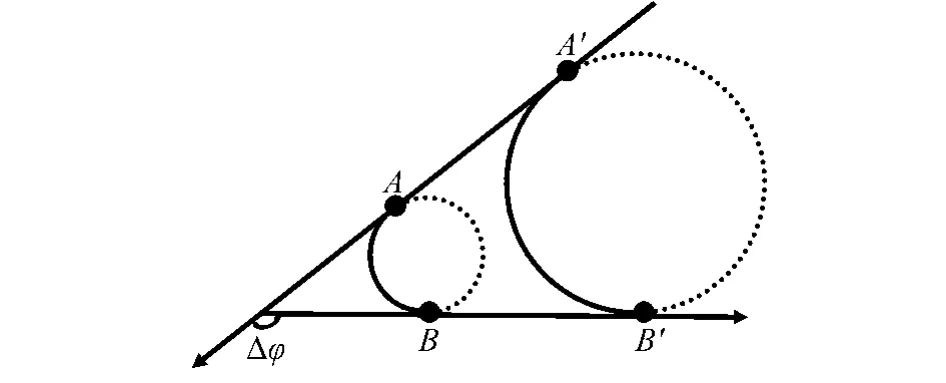
图1

图2
观察上面两图,曲线的弯曲程度与哪些量有关呢?
(1)如图1所示,弧长不等,切线转角相等的曲线弧,弯曲程度有何不同?
(2)如图2所示,弧长相等,切线转角不同的曲线弧,弯曲程度有何不同?
整个推导是由学生在思考的过程中完成的,让学生在体会到成功的喜悦的同时,也加深了对曲率概念的理解,避免了一知半解的死记公式。
再比如在讲解利用格林公式计算曲线积分时,我们依次给出以下问题:
通过对这几个相似题目的研究、探索,可以引领学生深层次地理解格林公式的适用条件,有效避免解题时机械地套用公式,锻炼思维的灵活性。
1.3 解决问题
解决问题的过程是一个完善提高的过程。有些问题学生给出的方案中可能会有一些不够完善的地方,甚至是错误,这就需要教师及时纠正总结,帮助学生规范解答过程,完善解题思路,提高数学素养和逻辑思维能力;有些问题还可能会有不同的解决方案,这需要教师引领学生总结比较,选出最佳方案。同时还应引导学生对所解决的问题进行延伸,举一反三,触类旁通。
比如上面推导出曲率的公式之后,可以带领学生去讨论直线、圆直至一般曲线的曲率,再结合前面提出的“火车脱轨”问题讨论铁路的缓和曲线,深入了解曲率在实际问题中的应用。再如在讲完拉格朗日中值定理之后可以给出“四条腿一样长的正方形椅子放在不平的地上是否总能放稳”这个例子,让学生体会到数学无处不在。
除了正常课堂教学外,我们采用多留思考题的方式,帮助学生养成深入思考、勤于思考的思维习惯。比如曲率一节讲完后,给出“你能找到自己的方法度量曲线的弯曲程度吗?”的问题让学生课后思考。
2 高等数学研究性教学方法
2.1 创建实践教学,促进学生的个性发展
高等数学虽不像物理、化学等学科一样有具体的实验操作,但也可以在教学中增加实践教学的环节,像数学实验、数学建模等,既能帮助学生理解所学知识,还能培养学生“用数学”的能力,进而提高创新能力。
数学实验是计算机技术和数学软件引入教学后出现的新事物,就是借助数学软件用实验的方法来学习掌握数学知识和解决数学问题。目的在于提高学生学习数学的积极性,提高学生对数学的应用意识并培养学生用所学的数学知识和计算机技术去认识问题和解决实际问题的能力,是学生认识数学规律、掌握数学技能的有效途径[6]。Matlab软件是一款常用的数学软件,它具有语言简洁紧凑、图形功能丰富、操作方便灵活的特点[7],在课堂上掌握了基本的数学概念之后,安排学生上机,尝试用Matlab软件解决相应的计算题,既可以解决课时不足的问题,提高效率;又为数学的思想与方法注入了更多、更广泛的内容,为学生自主解决工作学习中遇到的问题提供了方法、思路和经验。
在弥补数学知识远离生活实际的方面,数学模型是一个极好的学习题材[8],将数学建模的思想穿插到日常教学中去,将契合课程内容的模型纳入课程体系,可使学生对所学内容有更切肤的体验和深刻的理解。我们选取了一些学生感兴趣的实际问题,像存款利息、如何控制体重、如何合理购物、传染病传播速度等,每一章内容学完之后,给出一到两个问题,引领学生根据本章所学知识建立数学模型,并尝试用数学软件求解数学模型,将数学实验和数学建模有机结合,既增加了学生的学习兴趣,又培养了学生的建模能力,切实达到了“学有用的数学”的目的[9]。
此外,充分利用第二课堂,培养学生的创新精神。大学生蕴藏着巨大的学习潜力和探索热情,对有些问题,我们采用讨论班、小辩论的方式展开,让学生在课下搜集、阅读大量的材料之后到课堂上报告自己的论点、论据和证明方法。这样可增强学生的主动性,提高学生的学习兴趣,通过讨论、辩论,加深了对知识的理解,有利于培养学生主动学习、自我探索的自学能力以及发现问题、提出问题和解决问题的能力。我们还组织了多种多样的数学活动,像数学知识竞赛、数学建模竞赛、名师名家讲座等等,使学生参与其中,激发他们的热情,挖掘他们的潜能,有利于培养学生主动探索新知的学习习惯,营造积极向上的学习氛围。
2.2 构建立体化教学平台,提供优质教学资源
研究性教学仅仅依靠课堂是远远不够的,而应该向更广阔的空间、时间进行延伸,让学生学会自主获取知识,这就需要各种学习资源的有力支持。
(1)建立多媒介、多形态、多用途、多层次的教学资源库。
我们的资源库既包括与日常教学相配套的优质教材、教学辅导书、CAI课件、教学视频、习题库等,供学生课前课后自学使用,还包括一些涉及数学文化、数学应用的课外阅读材料,特别是一些英文经典文献,供学有余力的学生使用,以拓宽学生的视野,提高数学素养。
(2)充分发挥网络优势,建立网络互动教学平台。
研究性教学是一个沟通与协作的过程,网络正好提供了一个交流的空间[10]。为此我们建立了自己的教学网站,网站的建设以服务师生为目的,为方便学生查阅资料,我们将教学资源库中的电子资源分栏目上传,并建立清晰的栏目索引;为方便师生课下交流,还开设了网络答疑、讨论交流等栏目;我们还准备建立网络自测系统,便于学生及时对自己的学习情况进行检验。
此外,为丰富学生的课余生活,我们开设了数学文化、数学实验、高等数学应用等领域的公共选修课,满足不同专业学生对数学知识的需求,给学生更多的选择空间。
2.3 建立合理的教学评价体系,科学评价学生的学习过程
实施研究性教学的重点是教学过程而不是教学结果,评价方式应该由终结性评价转向过程性评价[11]。对教师的评价不能仅看板书是否工整,声音是否洪亮,层次是否清楚等,而应该从内容组织、信息传递、师生互动、课堂气氛、激发学生兴趣等方面进行综合评价。同时对学生的评价也应该从单一的闭卷考试向多元化的考核方式转化,应贯穿于研究性教学实施前、中、后的全过程[12],并从基本知识、基本能力、基本方法、基本素养、基本思想和基本活动经验等方面进行全面评价。为了调动学生平时学习的积极性,我们按照“1+1+x”的模式对学生进行综合考核,“1+1”是平时成绩加期末成绩,平时成绩主要根据学生日常的作业、出勤、课堂表现情况进行评价,期末考试重点考察学生对基本概念、基本理论、基本方法的理解和综合应用能力,尽量避免繁杂的计算证明题。“x”是一个开放性的评价,在教学过程中,结合所学知识,根据学生的专业特点,教师给出几道综合性的建模应用题,学生自主选择题目,自由结合,合作交流,学期末以小论文或实验报告的形式提交研究结果,教师给出综合评价。这样既拓展了学生的学习方式,锻炼了学生的研究能力,培养了学生的成就感,还为学生日后进行毕业设计打下了基础。
总而言之,高等数学由传统式教学向研究性教学的转变是一个长期而系统的过程,这需要我们广大的教师不断地充实自己,提高科学素养,同时也需要硬件的支持和学生的配合。
[1]中华人民共和国教育部.关于进一步加强高等学校本科教学工作的若干意见[J].中国大学教学,2005(2):4-5.
[2]叶奇明,陈一明.研究性教学在本科教育中的应用[J].内蒙古师范大学学报(教育科学版),2007,20(11):109.
[3]赵新平.研究性教学中教师角色的重塑[J].教育理论与实践,2011,31(1):61 -62.
[4]程向阳.对高等数学研究性教学的探讨与思考[J].阜阳师范学院学报(自然科学版),2009,26(1):58 -61.
[5]褚小婧,程向阳.大学数学研究性教学的实质与探索[J].大学数学,2011,27(1):16 -20.
[6]孟义平,蒋磊.工科大学数学实验教学的探索[J].江苏教育学院学报(自然科学版),2012,28(1):23 -24.
[7]王惠临,赵俊卿.Matlab在大学物理教学中的应用[J].山东建筑大学学报,2009,24(3):279 -281.
[8]李岚.高等数学教学改革研究进展[J].大学数学,2007,23(4):20-26.
[9]葛倩,李秀珍.专科高等数学应用型教学模式探索[J].科教文汇,2012(3):103-147.
[10]余达锦,杨淑玲.基于网络环境下的高等数学教学改革[J].江西财经大学学报,2004(5):118-119.
[11]佘远富,王庆仁.高校研究性教学评价体系的构建[J].高等工程教育研究,2011(6):111-115.
[12]王秀华.高校研究性教学课程评价体系构建研究[J].高等理科教育,2012(2):91-95.
